基于声光融合的气体温度和浓度二维重建

2015-01-13宋伟刘岩黄帆刘石

化工自动化及仪表 2015年11期

宋伟刘岩黄帆刘石

(华北电力大学能源动力与机械工程学院，北京 102206)

随着人们对电力需求的急剧增加，能源紧缺问题日益严峻。而对热力设备燃烧过程中温度和气体浓度的实时可靠监测，则是保证其安全、经济运行和实现自动控制的必要条件。

目前，国内外对温度和气体浓度的测量手段主要包括声学法[1，2]和光学法[3，4]。仅依据声波速度重建温度会受到重建区域内气体浓度分布的影响[5]，根据D-L模型能够利用声衰减和声速得到多原子混合气体的浓度，但是由于高温转动弛豫和振动弛豫机理的复杂性，该理论尚在研究阶段。激光光谱法在测量热力设备燃烧过程中的温度和气体浓度时虽然可以达到很高的精度，但是可调谐激光系统的价格比较昂贵。因此，寻找一种高效廉价且运行稳定的温度和气体浓度测量方法尤为重要。

通过对声光两种方法的研究，笔者提出基于声光融合的测量方法，通过对混合气体内声速和单一频率光谱积分吸收系数的测量，结合融合思想和CT理论[6]对燃烧区域内的温度场和气体浓度场同时重建，以获得较高的重建精度。

研究表明，混合气体中光谱积分吸收系数和声速均与混合气体浓度、温度成一定的函数关系。基于此，笔者通过测量混合气体的声速和固定光谱吸收系数，并利用二者同温度、浓度的关系，同时重建混合气体的温度与浓度。

1.1 近红外激光吸收系数与气体浓度和温度的关系

当一束频率为v(cm-1)的单色激光穿过燃烧区域时，其能量被吸收组分频率相同的气体吸收，其中入射光强I0和透射光强It遵循Lambert-Beer定律[7]：

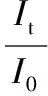
(1)

式中L——光程；

p——总压；

Sv(T)——测量用谱线在温度T时的谱线强度；

X——吸收气体摩尔浓度；

Sv(T)的表达式为：

(2)

式中c——光速；

E——最低能级的能量；

h——普朗克常数；

kB——玻尔兹曼常数；

Q(T)——分割函数；

Sv(T0)——参考温度T0下的谱线强度，其值可通过Hitran光谱数据库查询。

定义积分吸收系数A为：

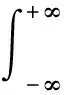
(3)

其中，αv为吸收系数。当压力p和光程L一定时，A为吸收组分浓度X和温度T的函数。

1.2 声速与气体浓度和温度的关系

声速与混合气体浓度和温度有如下关系[5]：

(4)

式中Mmix——混合气体平均分子质量；

R——普适气体常数；

T——混合气体温度，K；

γmix——混合气体定压热容与定体积热容之比。

其中Mmix与γmix的值取决于混合气体的浓度组成和温度。

1.3 气体浓度和温度的确定方法

以甲烷完全燃烧得到的混合气组CO2-水蒸气-N2-O2为例，建立混合气体吸收系数和声波速度与气体浓度、温度关系的三维模型(图1、2)。设混合气体总量为标准的1单位摩尔浓度，如此各气体浓度既能代表其所占比例又能代表其浓度，其中水蒸气的体积浓度的变化范围40‰～400‰，燃烧区域内温度的变化范围1 100～2 000K，总压101 325Pa，光程1m，参考温度296K。所选取的固定光谱频率与水蒸气的振动频率相同。

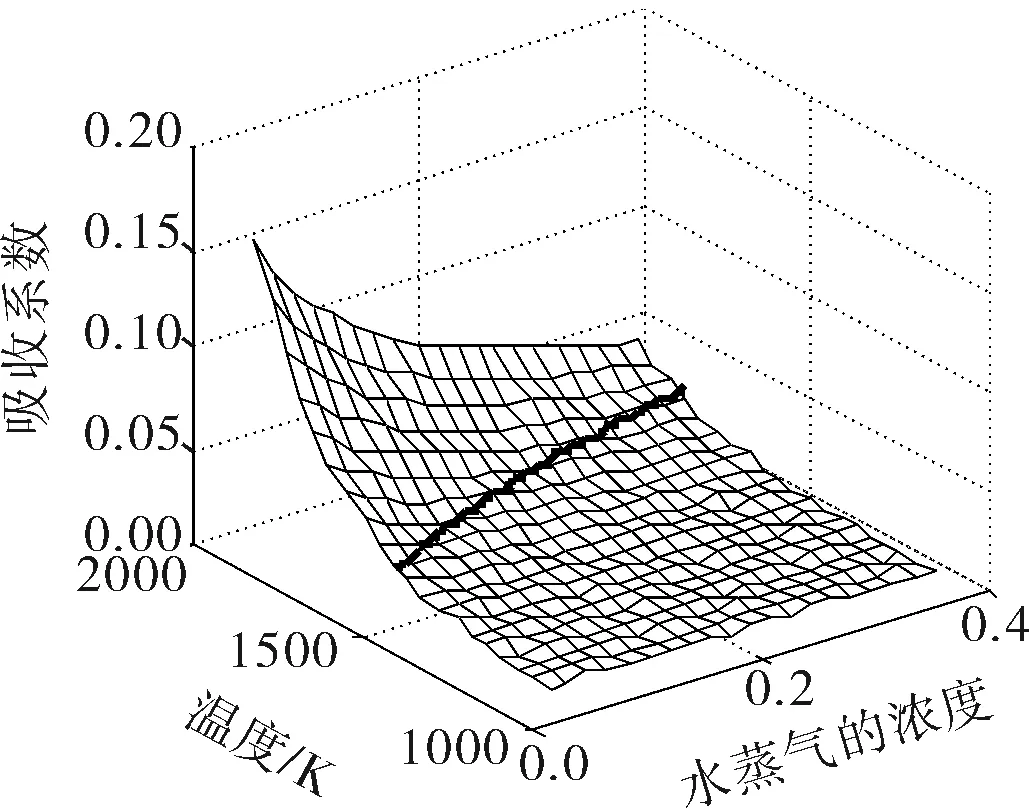
图1 混合气体吸收系数与温度、浓度的关系

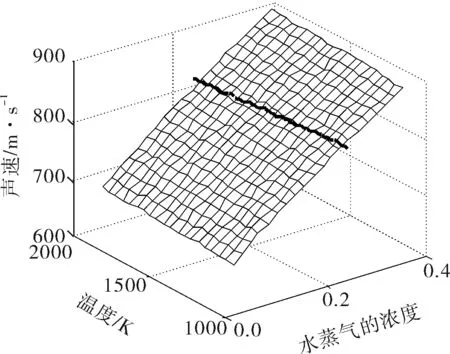
图2 混合气体声速与温度、浓度的关系

由图1可见，若测得混合气体的积分吸收系数A0，就能依据式(3)得到对应的吸收系数，然后在图1中画出相应的等值切面，其与吸收系数-温度浓度曲面交于一条曲线，该曲线上的点就是满足对应光谱吸收系数的所有气体温度和浓度的组合；同理，若测得混合气体的声速C0，同样可在图2画出一条曲线，然后将这两条曲线同时投影到混合气体温度浓度平面，交叉点就是此时混合气体的温度与浓度值，如图3所示。

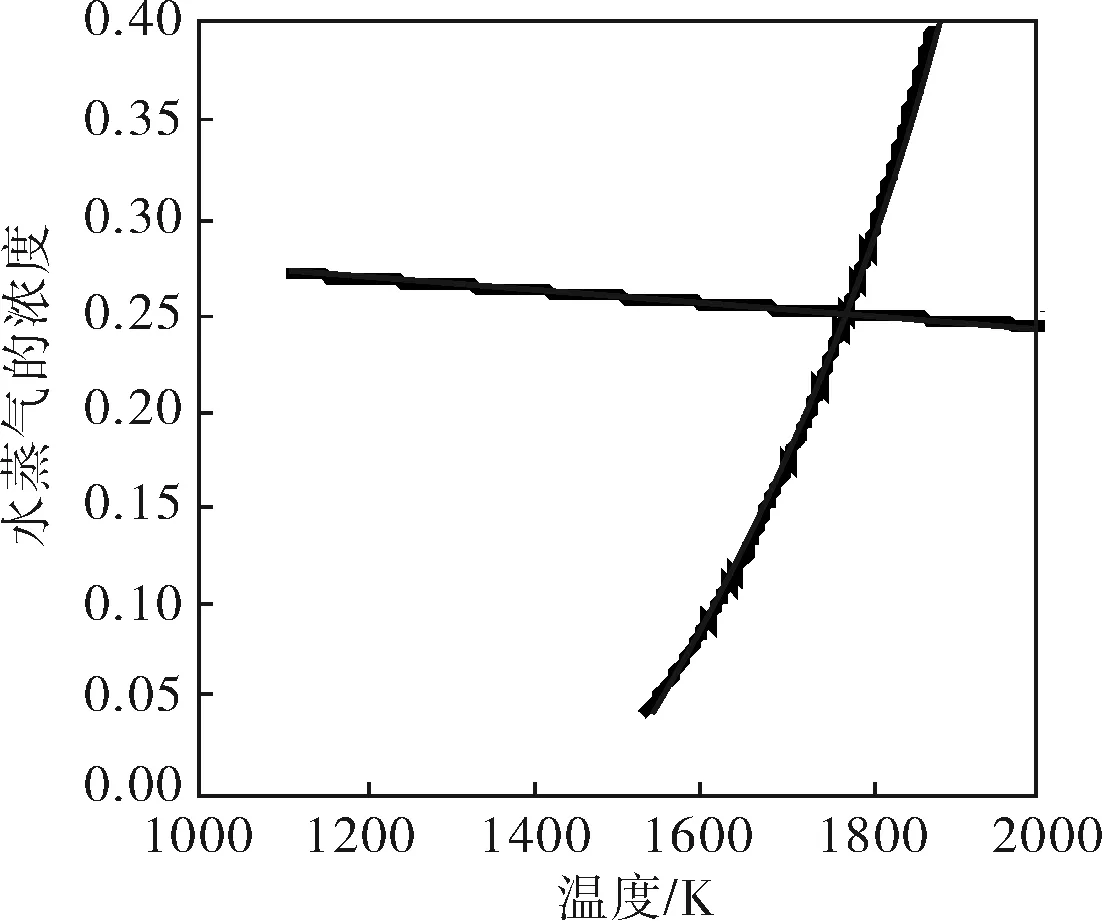
图3 固定光谱吸收系数和声速对应的温度浓度

1.4 气体浓度和温度的二维分布重建

将待测燃烧截面分成M×N个网格，每个网格的气体浓度和温度都是未知的，假设每个网格内的浓度和温度是均匀的，当频率为v的第j束激光束和第j条声波从同样的安装位置和同样的角度穿过待测截面区域(图4)，最终探头探测到的气体光谱积分吸收系数Aj和声波传播时间Gj是由穿越离散化区域的每个网格共同作用的结果，光谱吸收过程和声波传播过程可表示为：

(5)

(6)

式中c(m,n)——声波在第m行n列网格内的速度；

Lj(m,n)——第j束激光束或第j条声波穿越m行n列网格时的长度；

[S(T)X]m,n——激光在第m行n列网格内谱线强度与气体浓度的乘积；

α(m,n)——第m行n列网格内的吸收系数。

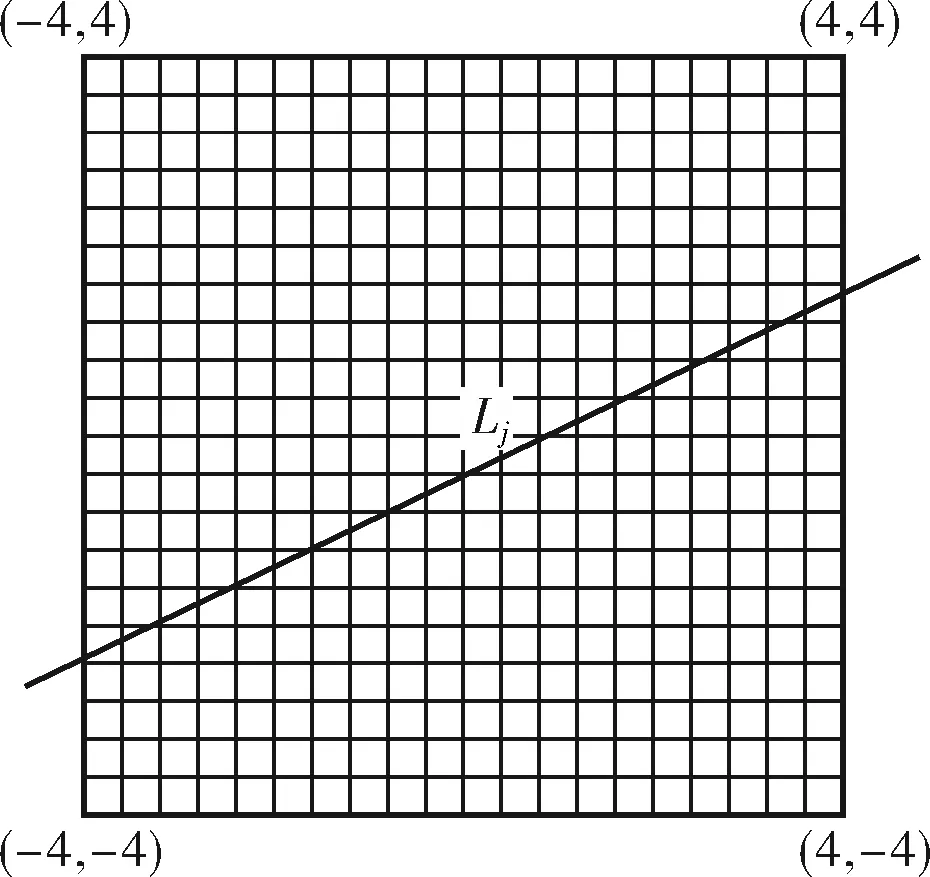
图4 激光束和声波线Lj

图像CT重建过程是通过测得的多条光路积分吸收系数和声波传播时间，借助某求解反问题算法确定每个网格内的吸收系数和传播时间，再结合声光融合理论得到每个网格内温度和气体浓度值的过程。

笔者提出的重建算法使用的是指数基函数[8]与广义逆相结合的方法，即分别用指数基函数逼近吸收率系数函数α(x,y)和声速倒数函数1/c(x,y)，即：

α(x,y)=∑εiφi(x,y)

(7)

1/c(x,y)=∑δjφj(x,y)

(8)

如此求解α(x,y)和c(x,y)的问题就转换成求解式(7)、(8)中两个系数向量ε和δ的问题，可抽象为：

A′X′=B

(9)

其中，X′为被求系数ε和δ组成的矩阵；A′为已知系数矩阵，代表所选取的基函数在所有燃烧区域划分的网格内积分值的矩阵；B为可测数据向量，代表所测光路光谱积分吸收系数和声波线路声波的传播时间。

2 数值仿真

针对甲烷完全燃烧区域不同处的温度和水蒸气浓度的重建，选取空间为8m×8m的区域，并离散为20×20个像素点，温度和水蒸气浓度在整个空间范围内是变化的，但由于划分像素点较密集，可近似认为每个像素点内水蒸气浓度和温度是稳定不变的。在仿真试验中，由于水蒸气和CO2均为甲烷完全燃烧后的产物，故CO2-水蒸气浓度比为1∶2，剩下的N2-O2按空气中的比例78∶21。环境温度T0=296K，压力p0=101325Pa。光学、声学传感器的布置如图5所示。

图5 光学、声学传感器布置

为使仿真过程符合实际重建过程，在仿真所用的测量数据中加入高斯白噪声，并对不同幅值的高斯白噪声带来的重建相对误差进行分析。

重建区域初始浓度与温度分布采用双Gauss函数模拟，为便于比较，设定不同的Gauss参数，选取两种特征工况：工况1，温度场双峰，浓度场单峰(图6a)；工况2，温度场单峰，浓度场双峰(图6b)。图6c、d是加入相对标准差为0.05的高斯白噪声后的两种重建工况。

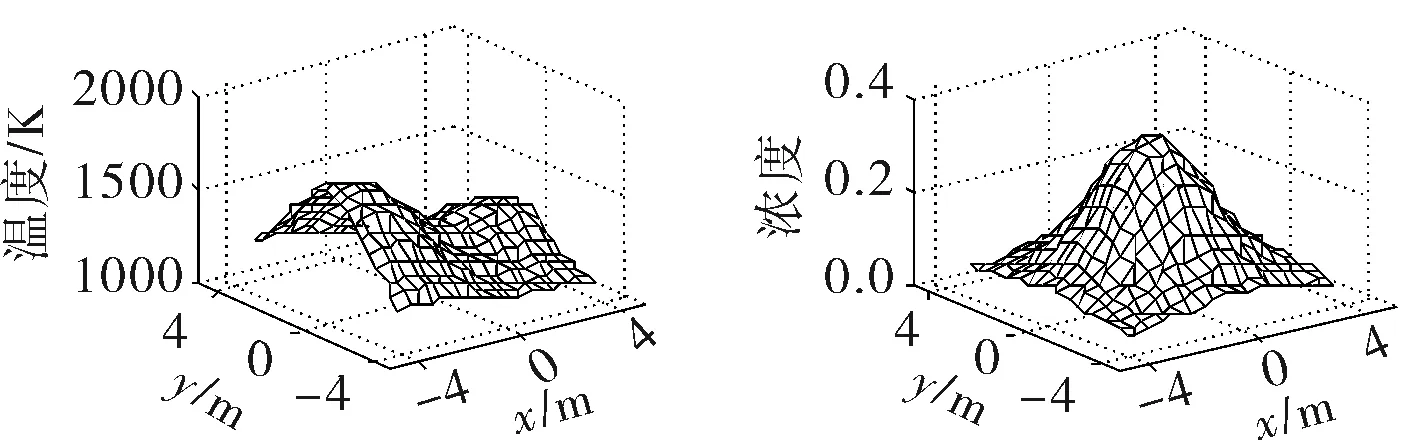
a. 工况1

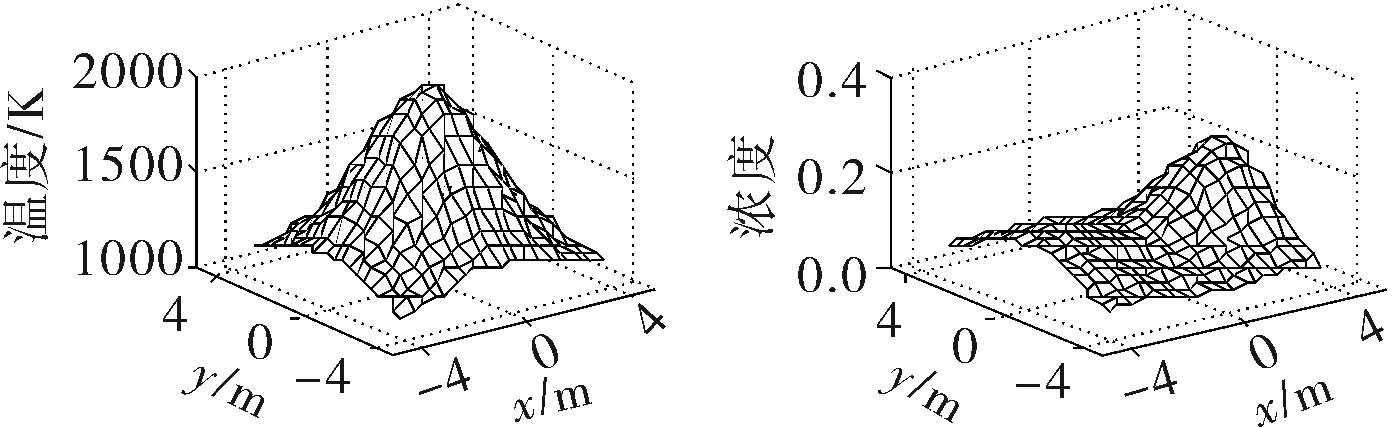
b. 工况2

c. 重建工况1

d. 重建工况2

可以看出，图6c、d中左图的温度重建与图6a、b的左图在分布规律和数值上基本吻合；而图6c、d中右图的浓度重建与图6a、b的右图在分布上满足单峰和双峰的特点，但在数值上有差别，特别是在高温区域差别较大，个别网格点相对误差甚至达到了30%左右。

综上所述，重建结果分布趋势和模型相吻合，表明声光融合方法是可行的。特别对于温度场的重建，其结果准确且抗干扰性较强。

3 重建结果讨论与误差分析

3.1 重建结果讨论

由重建结果可以看出，浓度场相对于温度场来说，重建结果较差，特别是在水蒸气浓度较高的区域和浓度分布较复杂的双峰分布时：一方面是因为重建算法上的问题，在谱分析时浓度场的低频成分可以用有限个基函数来近似，高频的细节部分却无法获得；另一方面是融合理论自身的问题，这可以通过声速与光谱积分吸收系数对于浓度与温度的灵敏度来解释，如图7所示。

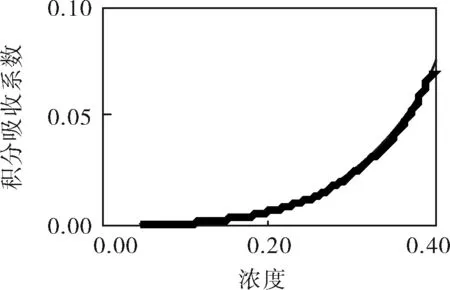
a. T=1500K，浓度从0.04～0.40变化时，积分吸收系数变化曲线

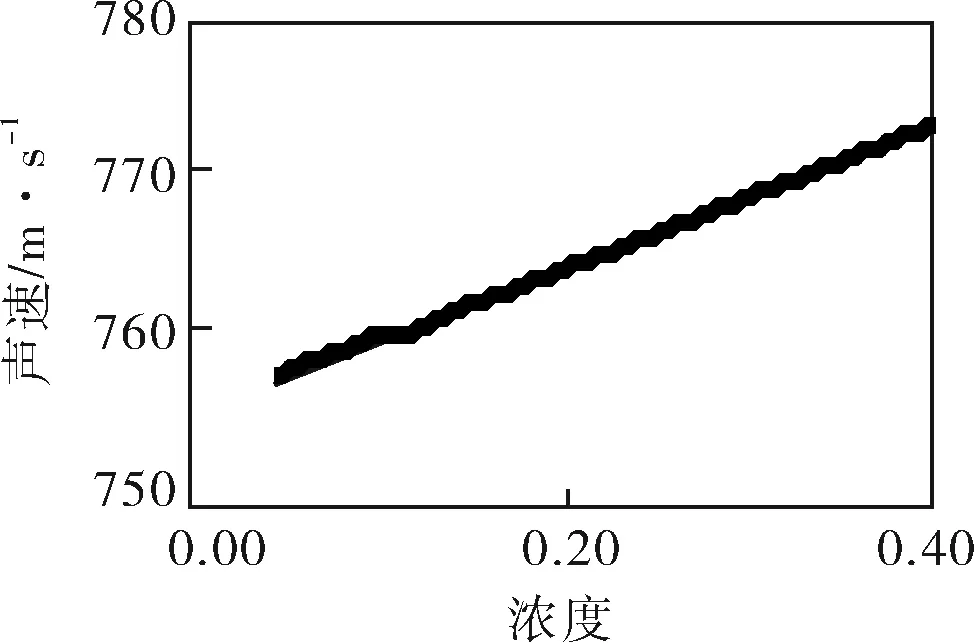
b. T=1500K，浓度从0.04～0.40变化时，声速变化曲线

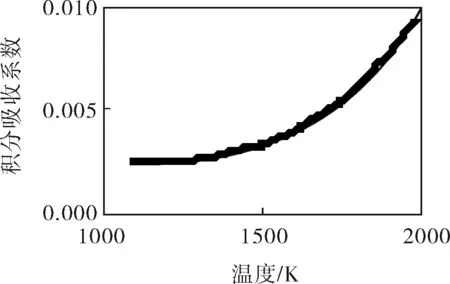
c. X=0.1，温度从1100～2000K变化时，积分吸收系数变化曲线

d. X=0.1，温度从1100～2000K变化时，声速变化曲线

浓度对声速的影响远小于温度对声速的影响，也就是说即便有较大的浓度变化，声速的改变并不大，那么通过声光融合法来确定浓度时，较难通过声速来反映浓度的变化，从而导致浓度场重建误差较大。

3.2 误差分析

通常在测量声速和光谱积分吸收系数时，会有一定的测量误差，图8给出了声波飞渡时间和光谱积分吸收系数测量误差对温度场和浓度场重建的影响，当随机误差标准差从0.00提高到0.05时，温度相对误差不超过8%，浓度误差在约10%，说明声光融合重建方法有较强的适应性，温度重建结果相对于浓度重建结果更好，但是浓度场重建误差不如温度场重建误差对测量结果敏感，这对于燃烧条件下温度和浓度的测量是很有益的，因为温度相对于浓度的变化是滞后的，故其实时测量误差相对较小。

图8 声波飞渡时间和光谱积分吸收系数测量误差对温度场浓度场重建的影响

利用笔者提出的声光融合理论重建甲烷完全燃烧区域温度场和浓度场的误差主要包括3部分：测量声波传播时间和光谱积分吸收系数的误差，主要取决于仪器精度和周围环境噪声的影响；重建过程中求解病态矩阵的逆带来的误差，由于工程实际中出于成本和重建速度的考虑不可能过多地增加测量信号，故主要从重建算法上进行改进，选择了重建结果较好的指数基函数和广义逆结合的算法；在确定声速和光谱积分吸收系数后，从理论上来说对图1、2气体的温度和浓度的网格划分越密集通过融合理论确定的待测区域网格内的温度和浓度越精确，但为了使重建具有实时性，不可能进行无限分割，根据精度和重建时间的综合考虑，选择对温度和浓度进行801×801的网格划分。