基于Curvelet稀疏表示的图像压缩感知重构算法

张 岩 任伟建 唐国维

(东北石油大学 a.计算机与信息技术学院；b.电气信息工程学院，黑龙江 大庆 163318)

近年来基于正交变换的稀疏表示方法大多采用离散余弦变换、小波变换、Contourlet变换及Curvelet变换等。离散余弦变换是一种全局变换，不能很好地描述图像的局部特征。传统的小波变换能够稀疏表示一维点状奇异特征，有效捕获点状奇异特征，因此被广泛应用于信号特征提取及信号去噪等领域[1，2]，但是图像中包含的纹理信息通常是以曲线状线条为基本特征，具有线状奇异性，所以不具备方向识别性的小波变换不是理想选择[3]。Contourlet变换将多尺度分析和方向分析同时进行，其支撑区间是具有随尺度变化长宽比的长条形结构，具有方向性和各向异性，Contourlet变换获取图像边缘的能力相对较强，但描述曲线状纹理并不理想。Curvelet是一种具有方向性的各向异性小波[4]，其曲线状基元和图像中曲线状纹理的特征类似，因此可以更有效地获取图像的纹理特征，实现稀疏表示。

文献[5，6]提出，压缩感知(Compressive Sensing，CS)理论根据信号本身的稀疏性与观测方式的非相关性，只要信号在某个变换域是稀疏或可压缩的，就可以用一个与稀疏表示不相关的测量矩阵对信号进行降维观测，并在接收端使用复杂的重构算法以较高的概率通过其低维观测值高精度重构原始信号[7]，突破了奈奎斯特采样定理的瓶颈，为在图像采集的同时压缩数据提供了理论依据。但是，目前在基于Curvelet变换的压缩感知重构方法中存在两个主要问题[8～10]：Curvelet变换虽然能够捕捉图像的曲线状纹理特征，在低频区域保留图像大部分的能量，但高频仍存在大量细节信息，而且各尺度之间的Curvelet变换系数相关性较强，当前基于Curvelet变换的图像CS处理方法忽略了利用Curvelet变换各尺度之间系数的相关性来保持高频细节信息；传统的求解图像CS重构的基追踪算法计算复杂度较高，即使处理常见尺寸的二维信号也非常耗时，而且二维图像的CS观测矩阵规模随原图像的尺寸增大而增加，不仅提高了存储和计算处理的成本，还使CS过程受计算机硬件条件的限制。为此，笔者提出一种基于Curvelet稀疏表示的图像分块压缩感知重构算法以解决上述问题。

1.1 Curvelet

Candès E J和Donoho D L提出了两种基于第二代Curvelet变换理论的快速离散Curvelet变换方法，分别是非均匀空间抽样的二维FFT算法和Wrap算法[11]。

第二代Curvelet变换直接在连续域进行定义，连续Curvelet变换中频率窗Uj将频域光滑地分成角度不同的环形，j为尺度，如图1所示，阴影部分表示一个标准楔形窗，为连续Curvelet变换的支撑区间。

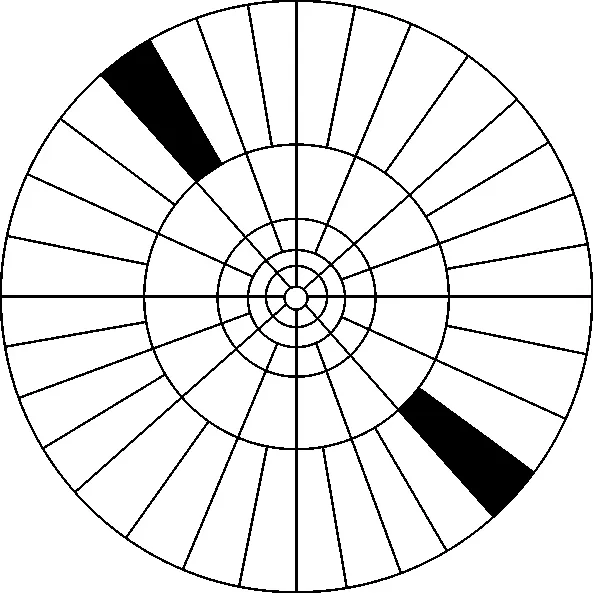
图1 连续Curvelet变换频率空间分块图

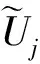
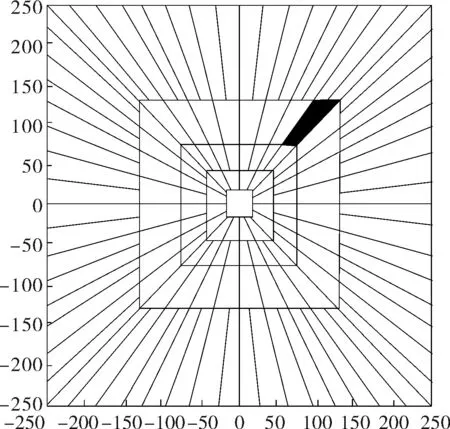
图2 离散Curvelet变换频率空间分块图

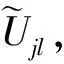
(1)

式中ω——傅里叶变换后的频域参量；

Φ——一维低通窗口的内积，各尺度低通窗口对应于图2中大小不同的笛卡尔方形窗。

二维图像x∈L2(R2)经过Curvelet变换，可表示为：

(2)

式中Cj,l,k——Curvelet基函数；

〈x,Cj,l,k〉——Curvelet变换后尺度为j、方向为l、位置k=(k1,k2)的系数。

1.2 多尺度相关性分析

对一幅512×512像素的babarla图像进行6级Curvelet分解，得到如图3所示的系数分布图。图中灰色条带是系数的间隔带，黑色局部出现亮点的条带是真实Curvelet系数条带。可以看出，沿方形窗由内而外Curvelet变换尺度依次增加，正中心包含了低频信息，最外层方形窗是最精细尺度的变换系数。可见Curvelet变换可以将大部分能量集中在第一级尺度，在2～6级变换尺度上，高频子带大部分系数值较小，并且在父级尺度下值较大的系数，在当前尺度下值也相应较大，各尺度之间相关性比较明显。

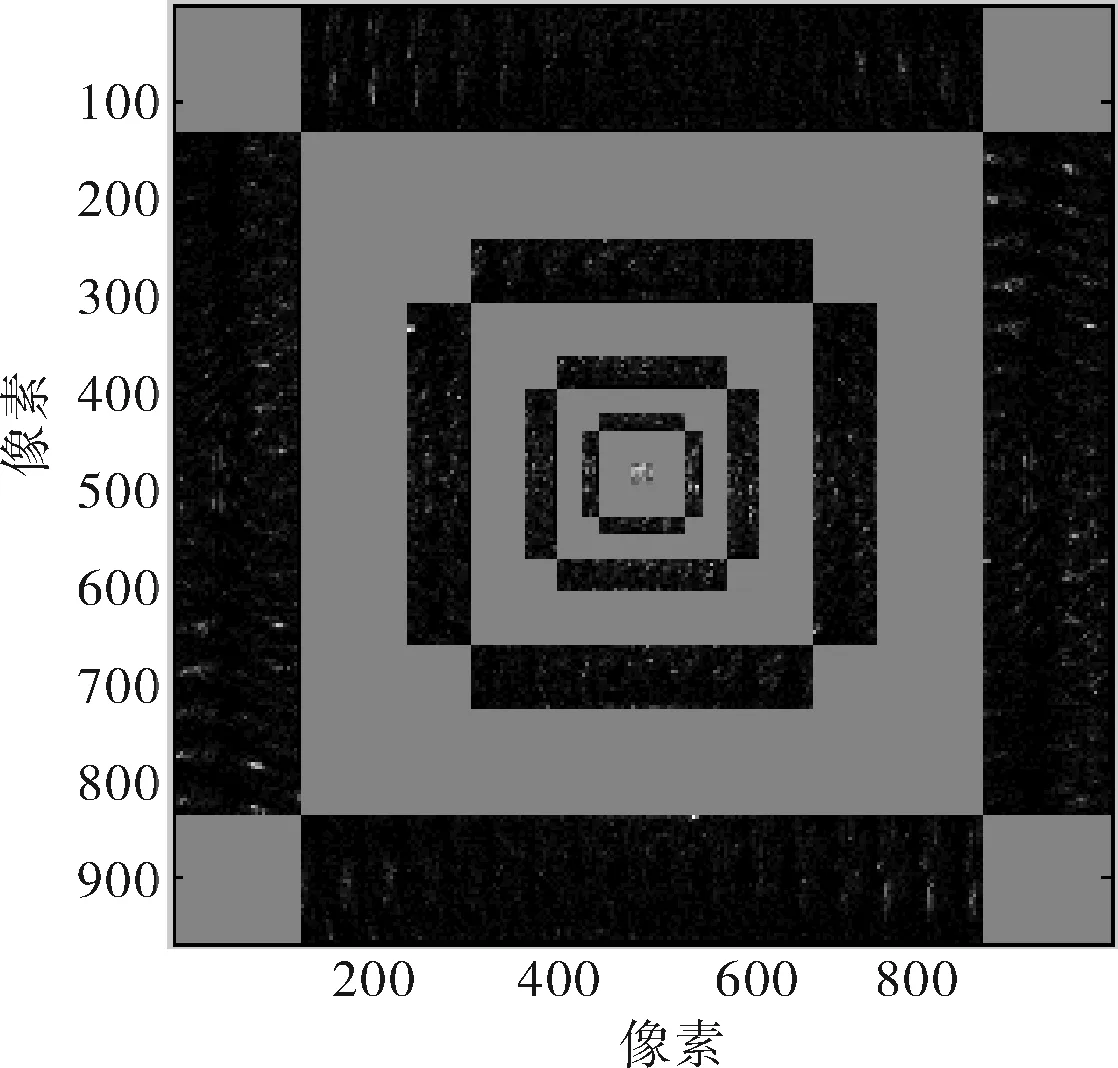
图3 Curvelet各尺度系数分布

Curvelet变换后的1～4级尺度系数结构见表1，每一级尺度j由多个方向l的系数组成。变换后得到的Curvelet系数以C{j}{l}(k1,k2)形式表示，其中j表示尺度，l表示方向，(k1,k2)表示尺度j上第l个方向上的坐标。在Curvelet变换各尺度之间对应方向上系数矩阵的尺寸不具有规则的倍数关系，与小波变换域多尺度之间的变换系数具有明确四叉树结构的父子关系分布有很大不同。

表1 Curvelet变换后的1～4级尺度系数结构

2 图像的分块随机观测模型

文献[12]首次提出基于分块压缩感知(Block Compressed Sensing，BCS)采样方法，图像矩阵x在采样过程中，首先被划分成不重叠的s个B×B子矩阵块，然后用相同的观测矩阵Φm×n对每个子矩阵块进行独立观测，得到观测向量集合：

yi|yi=Φm×nxi,i=1,2,…,s

(3)

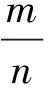
3 图像的重构模型

在图像的CS应用中，求解基追踪优化的主要问题在于基追踪算法计算复杂度高，即使处理常见尺寸的图像也非常耗时，于是降低计算复杂度成为众多学者的研究热点。近年来稀疏信号匹配追踪、正交匹配追踪及梯度投影等算法被先后提出[13～15]，这些算法虽然可以大幅降低计算复杂度，却是以降低重构信号质量为代价的。文献[16]提出光滑Landweber投影重构的BCS算法，其具有计算复杂度低、重构图像质量高于众多基追踪算法的优点。文献[17]基于小波变换各尺度之间与尺度内部的相关性，提出双变量收缩阈值迭代模型并获得了较好的去噪效果。双变量收缩阈值的迭代模型如下：

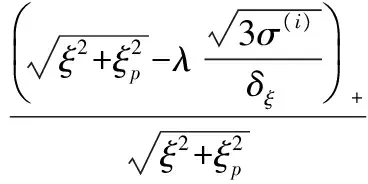
(4)

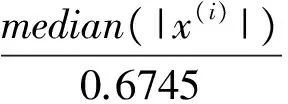
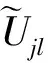
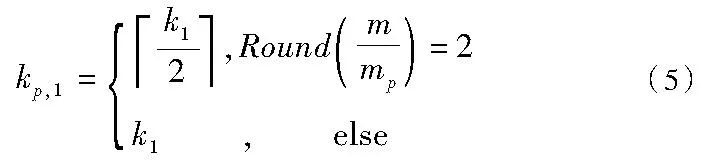
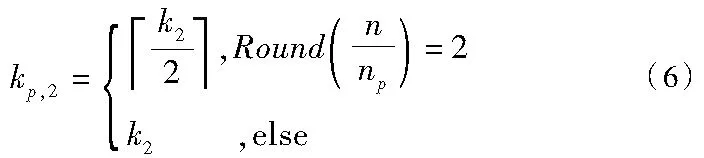
其中，Round表示四舍五入运算，┌ ┒表示向上取整运算。由Curvelet变换系数分布可得如果父级尺度的系数ξp值大，则子级尺度系数ξ值也相应较大，多尺度之间相关性较强。利用ξp可以较好地预测ξ值，从而能更好地保留细节信息，滤除迭代重构过程中的噪声。笔者提出的基于Curvelet稀疏表示各尺度间系数相关性的双变量收缩阈值的Landweber重构迭代式为：

(7)

(8)

式中C——Curvelet变换；

CT——Curvelet反变换；

T——阈值收缩算子；

x(k)——估计值经过阈值比较的调整值；

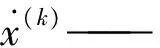
y——图像观测数据；

φ——测量矩阵；

γ——比例因子。

CS重构算法的具体步骤如下：

a. 初始化，给定迭代停止参数τ、图像分块观测矩阵φ、图像观测数据y，设迭代计数器k=0、Curvelet变换自适应阈值收缩算子为T、λ初值为λ0，给定η的初值；

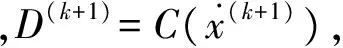
d. 多尺度双变量收缩阈值处理，V(k+1)=T(D(k+1))，其中V(k+1)为k+1次迭代系数阈值调整矩阵；

e. Curvelet反变换，xk+1=CT(V(k+1))，其中CT为Curvelet反变换；

f. 如果‖x(k+1)-x(k)‖2>τ转到步骤b，否则输出重构图像x=x(k+1)；

g. 算法结束。

4 实验结果与分析

对512×512像素的标准测试图像Lenna和Barbara分别采用基于Curvelet稀疏表示的图像分块压缩感知重构算法、DWT、Contourlet和DCT进行对比实验，图5、6分别给出了重构效果。可以看出DWT重构结果中的纹理区域振铃现象较严重；Contourlet具有获取两个信号几何轮廓特征的功能，结果中的纹理区域较清晰；DCT重构结果中的纹理区域模糊现象较严重；而笔者所提算法具有多尺度和多方向的识别能力，有利于图像中曲线状纹理的分辨，结合多尺度双变量收缩阈值迭代能够获得更好的重构图像效果。

图4 Lenna图像重构效果对比

图5 Barbara图像重构效果对比

表2分别给出了采样率为0.3时，上述4种算法重构效果的峰值信噪比(Peak Signal to Noise Ratio，PSNR)结果。可见笔者所提算法重构效果均高于其他3种算法，Lenna图像纹理区域相对较少，笔者所提算法的PSNR比其他算法平均提高0.74dB；Barbara纹理区域相对较多，笔者所提算法的PSNR比其他算法平均提高1.00dB。这都验证了笔者所提算法的有效性与稳定性。

表2 不同算法的PSNR数值比较结果 dB

5 结束语

为了研究图像的稀疏表示与重构问题，笔者提出了一种基于Curvelet稀疏表示的图像压缩感知重构算法，利用Curvelet变换优越的多尺度几何分析能力对图像曲线状纹理进行稀疏表示，结合BCS技术降低随机观测计算的复杂度。在图像重构过程中设计了基于Curvelet变换高频子带系数之间相关性的双变量收缩阈值迭代重构算法，实验结果也证实笔者所提算法可以很好地重构图像，在同一采样率下能够更好地保持图像的细节信息。

[1] 戴光,余永增,张颖,等.基于小波包分析和BP神经网络的滚动轴承非接触声发射诊断方法[J].化工机械,2008,35(5):274～277.

[2] 张勇,金学波.基于图像处理和小波去噪的化工信号分析[J].化工自动化及仪表,2007,34(1):69～72.

[3] 倪伟,郭宝龙,杨镠.图像多尺度几何分析新进展:Contourlet[J].计算机科学,2006,33(2):234～236.

[4] Candès E J,Demanet L,Donoho D L,et al.Fast Discrete Curvelet Transforms[J].Multiscale Modelingand Simulation, 2006,5(3):861～899.

[5] Candès E J,Romberg J,Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEE Transactions on Information Theory,2006,52(2):489～509.

[6] Donoho D L.Compressed Sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289～1306.

[7] 焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651～1662.

[8] 徐明华,李瑞,路交通,等.基于压缩感知理论的缺失地震数据重构方法[J].吉林大学学报(地球科学版),2013,43(1):282～290.

[9] 孔丽云,于四伟,程琳,等.压缩感知技术在地震数据重建中的应用[J].地震学报,2012,34(5):659～666.

[10] 叶慧,孔繁锵.基于Curvelet变换的图像压缩感知重构[J].计算机工程,2014,40(2):233～236.

[11] Candès E J,Donoho D L.New Tight Frames of Curvelets and Optimal Representations of Objects with Piecewise C2 Singularities[J].Communications on Pure and Applied Mathematics,2004,57(2):219～266.

[12] Gan L.Block Compressed Sensing of Natural Images[C].2007 15th International Conference on Digital Signal Processing.Cardiff:IEEE,2007:403～406.

[13] Tropp J A,Gilbert A C.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655～4666.

[14] Needell D,Vershynin R.Signal Recovery from Incomplete and Inaccurate Measurements via Regularized Orthogonal Matching Pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310～316.

[15] Figueiredo M A T,Nowak R D,Wright S J.Gradient Projection for Sparse Reconstruction:Application to Compressed Sensing and Other Inverse Problems[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(4):586～597.

[16] Sungkwang M,Fowler J E.Block Compressed Sensing of Images Using Directional Transforms[C].2009 16th IEEE International Conference on Image Processing(ICIP).Cairo:IEEE,2009:3021～3024.

[17] Sendur L,Selesnick I W.Bivariate Shrinkage Functions for Wavelet-based Denoising Exploiting Interscale Dependency[J].IEEE Transactions on Signal Processing,2002,50(11):2744～2756.

[18] 刘继承,张琳,董青松,等.基于二进小波变换的多尺度边缘细化检测[J].化工自动化及仪表,2014,41(6):641～646.

[19] 李伟,吴超群,王艳茹,等.基于小波神经网络的FRP复合材料损伤声发射信号识别[J].化工机械,2011,38(3):294～297.