转动惯量误差对汽车碰撞模型计算结果的影响

张 健， 张 鑫， 高金贵， 李 江

(1. 北华大学汽车与建筑工程学院，吉林 吉林132013;2. 人民交通出版社，北京100011;3. 吉林大学交通学院，吉林 长春130022)

文献［1］建立了以碰撞中心为坐标原点的典型汽车碰撞模型(以下简称模型)，根据现场和事故车辆的勘查信息，应用该模型能够计算碰撞前车速［2-3］，因此，参数的选取直接影响模型计算结果(以下简称计算结果)的准确性.目前，国内主要采用2 种方法确定参数:

(1)通过现场勘查确定车辆质量、碰撞中心坐标等［4］;

(2)根据经验公式或实验方法估算转动惯量［1］.

尽管对转动惯量测定方法进行了研究［5-6］，但鉴于交通事故的不可预知性和不可复制性，无法对已经碰撞变形的事故车辆进行转动惯量的准确测定，因此国内多采用经验公式根据事故车型进行转动惯量的估算.由于经验公式只考虑了车辆质量、车辆轮距、车辆长度等固定因素［1］，没有考虑车辆质量分布这一变化因素的影响. 事实上，考虑车辆质量分布不同的影响，即使相同质量同一车型的转动惯量也不相同. 因此，应用经验公式估算的转动惯量与事故车辆实际转动惯量之间难免存在误差.国外多采用基于实车碰撞试验和能够反映事故现场信息的数据库所开发的软件进行事故分析，输入现场信息计算与停车位置吻合的碰撞前车速［7-8］.由于没有建立相应的实车碰撞参数信息数据库，国内通常根据经验对计算结果进行调整.由于主观认识的差异，得到的计算结果难免存在误差［9］. 目前，国内对车辆转动惯量误差的研究较少［10-11］，而转动惯量误差对模型计算结果影响的研究更是少有报道.为了对事故做出准确分析，充分利用模型的优点，本文应用摄动理论完成了转动惯量误差对计算结果影响的定性和定量分析.

1 计算结果影响分析方法

应用动量方程和动量矩方程，结合车辆碰撞中心法向恢复系数和切向恢复系数公式，文献［1］中建立的模型为式中:

A0和A 为汽车碰撞前和碰撞后系数矩阵;

X0和X 为汽车碰撞前和碰撞后车速矩阵.

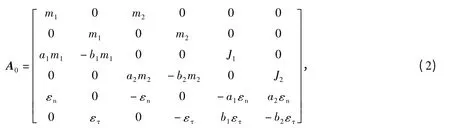
式中:

m1、m2分别为车辆质量;

a1、a2和b1、b2分别为车辆碰撞中心切向坐标和法向坐标(以下简称切向坐标和法向坐标);

J1、J2分别为转动惯量;

εn、ετ分别为车辆碰撞中心法向恢复系数和切向恢复系数.

将式(2)中第5 行和第6 行元素依次用-1，0，1，0，a1，- a2和0，-1，0，1，- b1，b2替换后得到A.

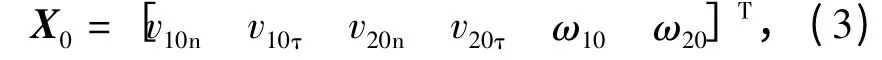
式中:

v10n和v20n分别为碰撞前车速法向分量;

v10τ和v20τ分别为碰撞前车速切向分量;

ω10和ω20分别为碰撞前车辆绕其各自质心的角速度(以下简称角速度).

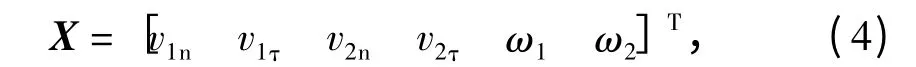
式中:

v1n和v2n分别为碰撞后车速法向分量;

v1τ和v2τ分别为碰撞后车速切向分量;

ω1和ω2分别为碰撞后角速度.

当估算的转动惯量J 存在误差ΔJ 时，汽车碰撞前系数矩阵A0和汽车碰撞后系数矩阵A 存在误差矩阵δA0和δA.

根据摄动理论［12-13］，计算结果为

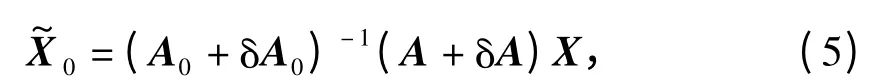
式中:

式中:

ΔJi为转动惯量误差;

JiA为转动惯量的准确值;

Ji为转动惯量的估算值;

i=1，2 分别为车辆1 和车辆2.

根据式(8)～(10)计算得到X.

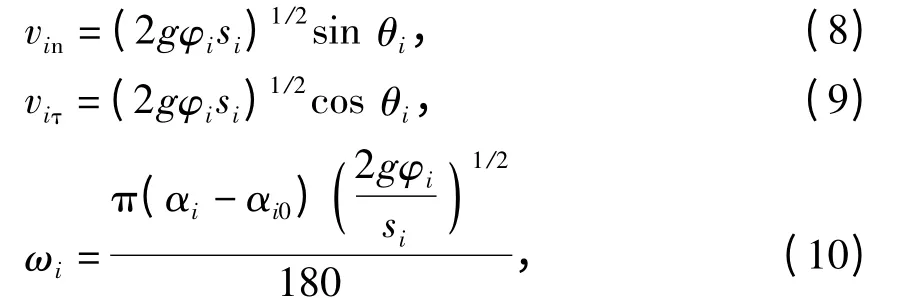
式中:

vin、viτ分别为碰撞后车速法向分量和切向分量;

g 为重力加速度;

φi为路面附着系数(以下简称附着系数);

si、θi分别为碰撞后车辆滑行距离和滑行方向角(以下简称滑行距离和滑行方向角);ωi为碰撞后角速度;

αi、αi0分别为碰撞后车辆停止方向角和碰撞前车速方向角(以下简称停车方向角和车速方向角).

2 分析方法应用

案例介绍:某城市道路平面交叉口处，一辆面包车由西往东与另一辆自南向西左转的轿车发生碰撞，轿车(车辆1)前部右端撞击面包车(车辆2)的右侧面，碰撞导致两车严重变形. 计算碰撞前车速，所需资料见表1.

根据车辆碰撞变形情况，选取车辆碰撞中心法向恢复系数εn=0.30、车辆碰撞中心切向恢复系数ετ= -0.906 5.

将表1 中数据代入式(1)、(2)、(8)～(10)，则有

X0=［0.475 3 11.502 5 8.020 4 -8.200 6，-0.349 0 0.320 4］T，v10=3.6［(v10n)2+(v10τ)2］1/2=

41.444 3 km/h，

其中，

3.6 为速度单位换算系数(1 m/s=3.6 km/h)，

v20=41.294 5 km/h，

α10=arctan(v10n/v10τ)=2.366 2°，

α20= -44.363 5°，

ω10= -0.349 0 rad/s

ω20=0.320 4 rad/s，这里，车辆逆时针转动时，角速度为正值，反之为负值.

文献［1］指出:当转动惯量误差不超过30%时，车速估算的置信度为95%.为此，以表1 中

J1=4 800 kg·m2，

J2=1 300 kg·m2

为准确值，在转动惯量相对误差［14］±30%范围内，分析实际应用中转动惯量误差的3 种形式(ΔJ1;ΔJ2;ΔJ1和ΔJ2)对计算结果的影响规律.

表1 事故分析数据Tab.1 Data for accident analysis

建立的分析指标为

式中:

EJi为转动惯量相对误差;

JiA为转动惯量的准确值;

Ji为转动惯量的估算值;

Evi0为ΔJi对碰撞前车速的影响误差;

vAi0为碰撞前车速的准确值;

vi0为存在ΔJi时的碰撞前车速;

Eαi0为ΔJi对车速方向角的影响误差;

αAi0为车速方向角的准确值;

αi0为存在ΔJi时的车速方向角;

Eωi0为ΔJi对碰撞前角速度的影响误差;

ωAi0为碰撞前角速度的准确值;

ωi0为存在ΔJi时的碰撞前角速度.

上述公式中:

J1A=4 800 kg·m2;

J2A=1 300 kg·m2;

vA10=41.731 8 km/h;

vA20=43.157 0 km/h;

αA10=1.109 7°;

αA20= -45.701 6°;

ωA10= -0.017 8 rad/s;

ωA20=0.199 0 rad/s.

根据式(5)，转动惯量误差对计算结果的影响如图1 ～4 所示.

图1 ΔJ1 对计算结果的影响Fig.1 Influence of ΔJ1 on the simulation results

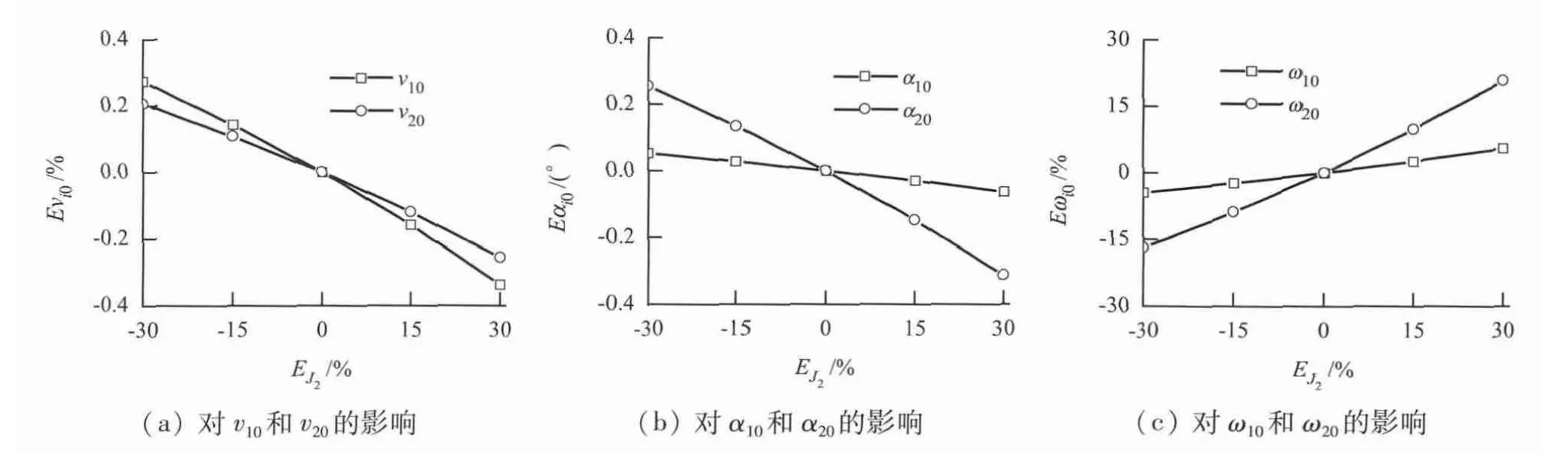
图2 ΔJ2 对计算结果的影响Fig.2 Influence of ΔJ2 on the simulation results

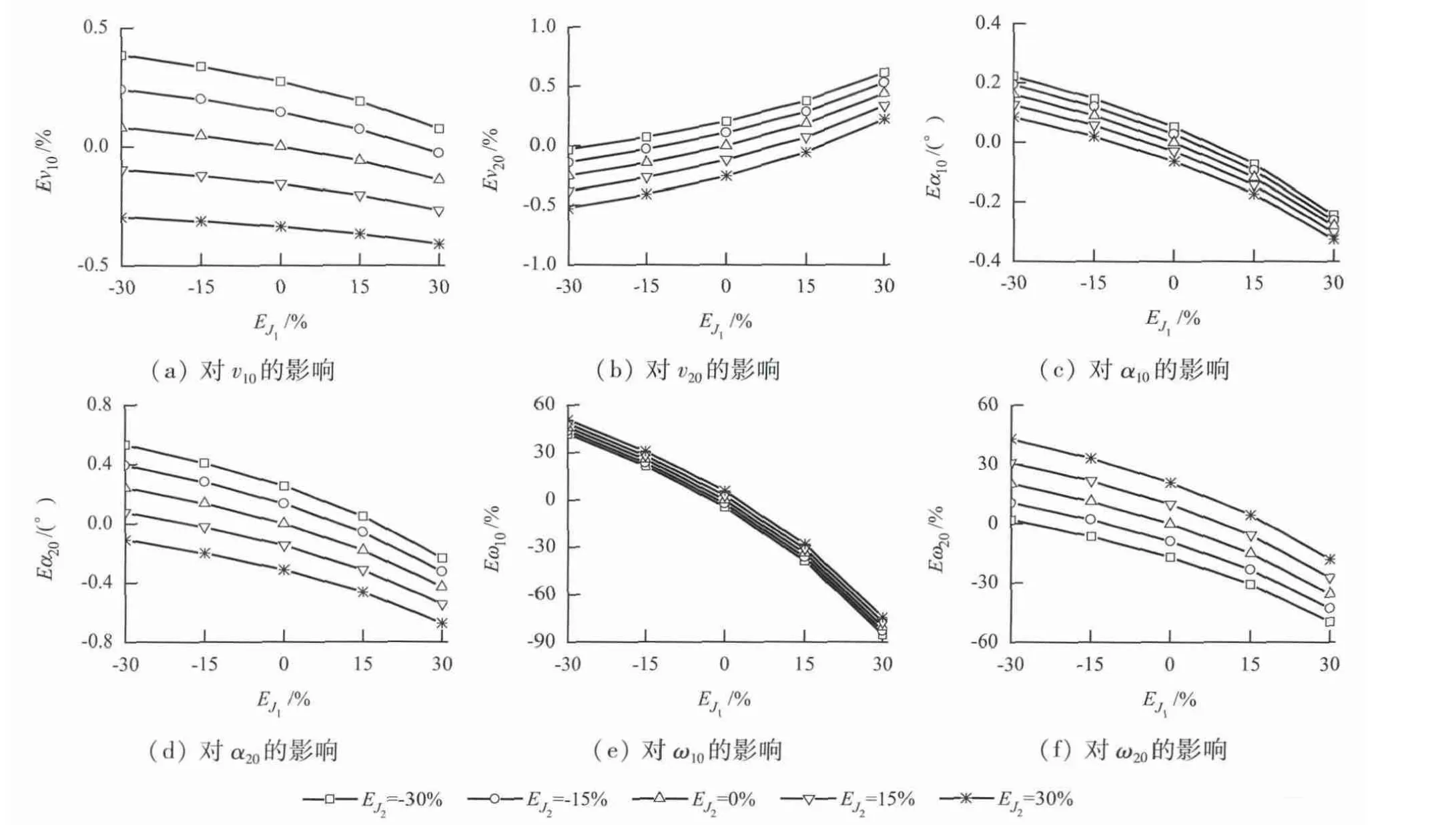
图3 ΔJ1 连续变化下ΔJ1 和ΔJ2 对计算结果的影响Fig.3 Influence of ΔJ1 and ΔJ2 on the simulation results when ΔJ1 changes continuously

图4 ΔJ2 连续变化下ΔJ2 和ΔJ1 对计算结果的影响Fig.4 Influence of ΔJ2 andΔJ1 on the simulation results when ΔJ2 changes continuously

3 影响程度评价

计算结果表明:图1 ～4 中的曲线变化规律具有线性特征.根据工程实际，每条曲线平均斜率反映转动惯量误差对计算结果的影响程度.建立评价指标为

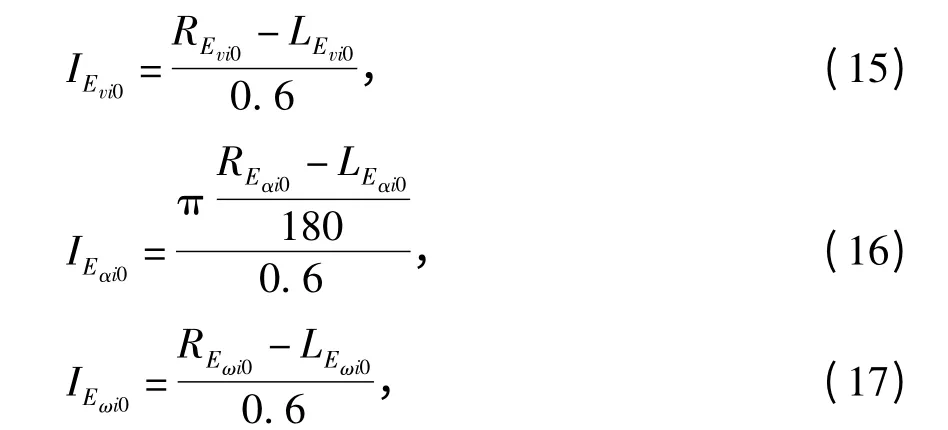
式中:

IEvi0为碰撞前车速曲线的平均斜率;

REvi0、LEvi0为图1 ～4 中每条碰撞前车速曲线右端数值和左端数值;

IEαi0为车速方向角曲线的平均斜率;

REαi0、LEαi0为图1 ～4 中每条车速方向角曲线右端数值和左端数值;

IEωi0为碰撞前角速度曲线的平均斜率;

REωi0、LEωi0为图1 ～4 中每条碰撞前角速度曲线右端数值和左端数值.

影响程度的计算结果列于表2 和表3，表中:“-”表示曲线左侧高右侧低，反之表示曲线左侧低右侧高;绝对值表示转动惯量误差对计算结果的影响程度，绝对值越大，影响程度越严重.

表2 ΔJ1 或ΔJ2 的影响程度Tab.2 Influence degree of ΔJ1 or ΔJ2

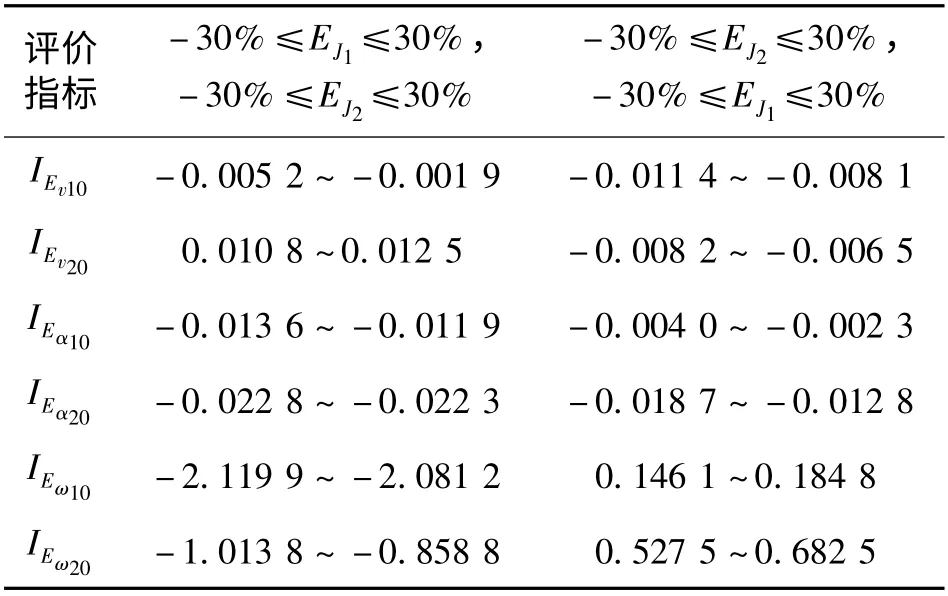
表3 ΔJ1 和ΔJ2 的影响程度Tab.3 Influence degree of ΔJ1 and ΔJ2

由表2 可见:

(1)ΔJ1对碰撞前车速的影响程度，v10＜v20，

(2)ΔJ2对碰撞前车速的影响程度，v10＞v20;

(3)ΔJ1、ΔJ2对车速方向角的影响，α10＜α20;

(4)ΔJ1对碰撞前角速度的影响程度，ω10＞ω20;

(5)ΔJ2对碰撞前角速度的影响程度，ω10＜ω20.

结果表明:ΔJ1或ΔJ2对碰撞前车速和碰撞前角速度的影响比车速方向角更复杂;ΔJ1或ΔJ2对碰撞前车速的影响具有误差交换效应;ΔJ1或ΔJ2对碰撞前角速度的影响具有误差传递效应;ΔJ1或ΔJ2对车速方向角的影响，轻车大于重车.

由表3 可见:

(1)ΔJ1和ΔJ2对碰撞前车速的影响程度，

v10＜v20;

(2)ΔJ2和ΔJ1对碰撞前车速的影响程度，

v10＞v20;

(3)ΔJ1和ΔJ2、ΔJ2和ΔJ1对车速方向角的影响，α10＜α20;

(4)ΔJ1和ΔJ2对碰撞前角速度的影响程度，

ω10＞ω20;

(5)ΔJ2和ΔJ1对碰撞前角速度的影响程度，

ω10＜ω20.

结果表明:ΔJ1和ΔJ2或ΔJ2和ΔJ1对碰撞前车速和碰撞前角速度的影响比车速方向角更复杂;ΔJ1和ΔJ2或ΔJ2和ΔJ1对碰撞前车速的影响具有误差交换效应;ΔJ1和ΔJ2或ΔJ2和ΔJ1对碰撞前角速度的影响具有误差传递效应;ΔJ1和ΔJ2或ΔJ2和ΔJ1对车速方向角的影响，轻车大于重车.

4 结果应用

在上述分析的基础上计算满足精度要求的转动惯量.

(1)精度要求

根据文献［15］，以|IEvi0作为转动惯量合理取值范围的约束条件反推转动惯量误差3 种形式所对应的EJi范围，从而确定满足计算结果精度要求的Ji范围.

(2)转动惯量取值范围

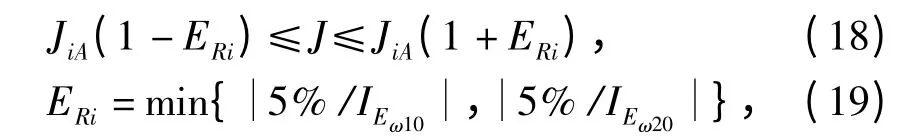
式中:ERi为误差范围;

J 为转动惯量;

IEω10和IEω20从表2 或表3 中选取.

根据式(18)～式(19)，实例中满足计算结果精度要求的Ji列于表4.

表4 转动惯量取值范围Tab.4 Value ranges of the rotational inertia

5 结 论

应用摄动理论和参数误差原理能够定性定量地分析转动惯量误差对计算结果的影响.分析结果表明:

转动惯量误差对碰撞前车速和碰撞前角速度的影响分别具有误差交换效应和误差传递效应;转动惯量误差对碰撞前车速和碰撞前角速度的影响程度，后者远大于前者. 应用分析结果能够确定满足计算结果精度要求的转动惯量取值范围.

致谢:吉林市科技发展计划项目资助(20090404).参考文献:

［1］ 许洪国. 汽车事故工程［M］. 北京:人民交通出版社，2004:77-85.

［2］ 中华人民共和国公安部. GA/T643—2006 典型交通事故形态车辆行驶速度技术鉴定［S］. 北京:中国标准出版社，2006.

［3］ 许海华. 一起交通事故中车辆碰撞速度的分析计算［J］. 长春大学学报，2010，20(6):42-45.XU Haihua. Analysis and calculation of vehicle collision speed in a traffic accident［J］. Journal of Changchun University，2010，20(6):42-45.

［4］ 张健，张鑫，高金贵. 基于动量定理的汽车碰撞模型的同一性研究［J］. 北华大学学报:自然科学版，2011，12(5):590-593.ZHANG Jian，ZHANG Xin，GAO Jingui. Identity research of vehicle collision models based on the momentum theorem［J］. Journal of Beihua University:Natural Science，2011，12(5):590-593.

［5］ 查佳韵，刘勇，程金华，等. 基于扭杆摆的汽车动力总成惯量参数测量实现［J］. 中国测试，2011，37(2):17-20，29.ZHA Jiayun，LIU Yong，CHENG Jinhua，et al.Realization of measuring auto powertrain inertia parameters based on torsion pendulum［J］. China Measurement ＆ Test，2011，37(2):17-20，29.

［6］ 刘昶. 三线扭摆系统测量刚体转动惯量试验方法改进［J］. 汽车科技，2011(3):67-71.LIU Chang. Improvement of experimental identification method with trifilar torsional pendulum for rigid-body's moment of inertia［J］. Auto Mobile Science ＆Technology，2011(3):67-71.

［7］ PRENTKOVSKIS O，SOKOLOVSKIJ E，BARTULIS V.Investigating traffic accidents:a collision of two motor vehicles［J］. Transport，2010，25(2):105-115.

［8］ NEADES J，SMITH R. The determination of vehicle speeds from delta-V in two vehicle planar collisions［J］.Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2011，225(1):43-53.

［9］ 张健，张鑫. 汽车碰撞模型中力学参数误差对碰撞前车速的影响［J］. 西南交通大学学报，2011，46(2):259-263.ZHANG Jian，ZHANG Xin. Influence of mechanics parameter errors on pre-impact speed of vehicle in vehicle collision models［J］. Journal of Southwest Jiaotong University，2011，46(2):259-263.

［10］ 迟占铎，徐鑫莉，张心明. 扭摆法测转动惯量的误差分析［J］. 长春理工大学学报:自然科学版，2012，35(1):36-42.CHI Zhanduo，XU Xinli，ZHANG Xinming. Error analysis of the moment of inertia using torsion pendulum method［J］.Journal of Changchun University of Science and Technology:Natural Science Edition，2012，35(1):36-42.

［11］ 聂信天，史庆春，顾浩，等. 拖拉机转动惯量测量及误差分析［J］. 机械科学与技术，2012，31(8):1325-1328.NIE Xintian，SHI Qingchun，GU Hao，et al. Method of measuring the moment of inertia of tractors and the error analysis［J］. Mechanical Science and Technology for Aerospace Engineering，2012，31(8):1325-1328.

［12］ 程云鹏，张凯院，徐仲. 矩阵论［M］. 西安:西北工业大学出版社，2013:12-440.

［13］ 张健，张鑫. 汽车碰撞改进模型的参数敏感性分析［J］. 西南交通大学学报，2010，45(3):451-456.ZHANG Jian，ZHANG Xin. Parameter sensitivity analysis in improved vehicle collision models［J］.Journal of Southwest Jiaotong University， 2010，45(3):451-456.

［14］ 徐涛. 数值计算方法［M］. 长春:吉林科学技术出版社，2002:2-12.

［15］ 张健，张鑫，李江，等. 典型汽车碰撞模型自选参数的敏感性分析［J］. 汽车工程，2012，34(10):905-908.ZHANG Jian， ZHANG Xin， LI Jiang， et al.Sensitivity analysis of selected parameters in typical vehicle collision models［J］. Automotive Engineering，2012，34(10):905-908.