基于贝叶斯决策的航空影像自动配准

张帅毅， 李永树， 蔡国林

(西南交通大学地球科学与环境工程学院，四川 成都610031)

基于影像处理技术的目标监测，按监测平台的不同可分为固定摄像头和移动摄像头.相对于固定摄像头，移动摄像头由于平台振动、旋转、倾斜等，导致获取同一区域的影像间存在平移、旋转、缩放等问题，极大地增加了影像自动配准难度，进而影响运动目标信息的有效提取［1］. 提高移动平台影像配准精度对于目标的追踪监测及目标运动参数精确估计等具有重要意义.

目前影像配准方法主要包括区域灰度配准、图像特征配准等［2］，其中区域灰度配准通过计算局部或全局灰度相关性，估计影像间的变换［3］. 文献［4］通过计算相邻航空影像间全局互信息，迭代计算影像全局变换模型，实现影像配准，但区域灰度配准计算量大，且复杂场景下容易失效. 图像特征配准通过提取影像特征点及特征点匹配，估计影像间变换模型，对于图像畸变及遮挡具有一定的鲁棒性，是影像配准常用的一种方法.

图像特征配准过程主要有特征提取、特征匹配、影像变换矩阵估计及待配准影像的重采样［5］.首先应用特征提取算法(传统Harris、SIFT［6］、SURF［7］等)提取参照影像和待配准影像特征点，并采用FLANN、KNN 等算法，在特征描述子空间中寻找匹配特征点;然后选择影像配准变换模型，通常在航空影像配准中选取仿射变换、透视变换等;最后基于匹配特征点集，采用最小二乘法［8］、随机一致性测试法(RANSAC)［9］等方法估计最优变换模型参数，变换校正、重采样实现影像配准.

还有一些研究通过在影像频率域计算相位相关的方法，进行影像配准［10］;文献［1，11］对影像进行极坐标变换，在极坐标空间实现配准;文献［12］通过直接定向的方法进行航空影像配准，但该方法需要高精度POS 数据支持.

在特征匹配过程中，FLANN、KNN 等匹配主要依赖特征描述子，容易导致误匹配，通常需要进一步筛选，进行特征精匹配.文献［13］在航空视频流配准应用中采用光流法来精确匹配特征点;文献［14］通过加入特征点的空间邻近约束关系来实现特征点的精确匹配.目前的特征匹配算法在一般的固定摄像平台或高帧频、小视场、短物距的移动摄像平台影像处理中取得了较好的效果，但对于低帧频、大视场、长物距(高航高)的航空移动摄像平台，上述研究由于没有充分考虑像点对应地面点高程起伏产生的像点投影差异，在基于移动平台(如无人机、航空遥感等)的目标监测应用中，不同高程面的特征匹配导致航空影像配准精度降低.

基于此，顾及像点投影差对影像配准的影响，本文提出了一种基于贝叶斯决策理论的像点投影差消除方法，并选用KIT AIS 数据［15］进行实验，比较分析投影差消除前后的配准影像差分视觉效果和信息熵变化，以验证该方法的有效性.

1 基于贝叶斯决策的投影差消除及影像配准方法

航空影像由于帧频率较低(2 Hz 左右)，场景变化大，且易受像点投影差影响，使得影像间的配准非常困难.因此，在目标监测过程中，需要事先估计影像的全局运动，实现在基准高程平面或基准面上的影像配准，其中基准面由目标监测过程中待监测目标所在视平面确定.

1.1 像点投影差影响及规律

航摄过程中，由于中心投影模式、姿态变化、地形起伏等因素的影响，使得相邻影像间存在像点投影差，且投影差随摄入角等因素的变化而变化，从而导致不同影像的同名像点存在不同的投影差.如图1 所示，设相邻摄站影像为A1、A2，S1、S2分别为A1、A2的摄站点(假定两幅影像航高一致)，地面点为P，θ1、θ2分别为P 点在A1、A2上的摄入角.

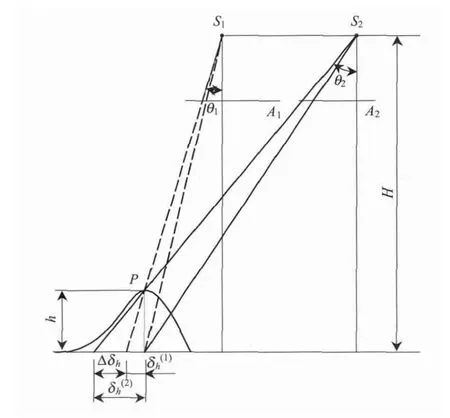
图1 像点投影差变化Fig.1 Change of projection difference

根据中心投影原理，可得P 点在A1、A2上的像点投影差:

由式(1)可得，两幅影像中P 的投影差变化为

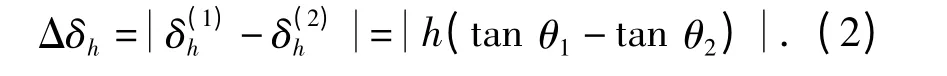
由式(2)可知，基准平面上的点h =0，理想状态下像点投影差变化为0;在相邻影像航高相近的情况下，像点投影差变化与相对高程h 及摄入角θ有关.实际上，受随机误差的影响，基准平面和非基准平面上均存在不同程度的像点投影差变化，且这种变化具有正态随机分布特性(已通过统计验证，见2.2 节).

1.2 基于贝叶斯决策的消除方法

针对像点投影差问题，可根据贝叶斯概率决策原理［16］，首先使用样本区匹配特征点集的先验概率分布和类条件概率分布，计算待分类影像特征点匹配在不同模式类下后验概率分布，然后根据后验概率的大小对待分类特征匹配点对进行分类，并加以筛选，从而消除投影差问题.

设样本集Xn×1，即n 个匹配特征点对的集合，其中1 个样本特征就是匹配特征点对的投影差变化(见式(2)). 样本有两类:基准面匹配与非基准面匹配，设为{ω1，ω2}.按贝叶斯决策原理，设P(x∈ωi)为样本集中匹配点对x 属于不同类别ωi的先验概率密度为ωi类匹配点对中样本x 的概率密度，即类条件概率密度为像点投影差变化为x 时，x 属于ωi的概率密度，即后验概率密度.

设xunk为待确定匹配类型的特征点对，在已知的情况下，根据贝叶斯决策原理可知:

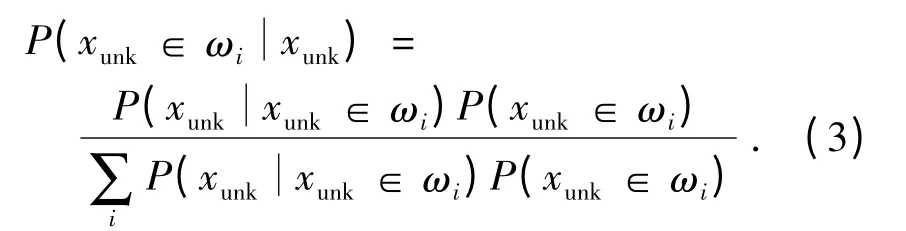
取具有最大后验概率的类别ωi为xunk:

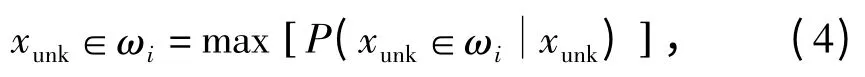
其中，通过统计样本区域点对集合的概率分布，可计算出离散的P(x∈ωi)，从而得到P(xunk∈ωi).此外，样本投影差变化经检验服从正态分布，即，通过计算类别内像点投影差变化的均值和方差可估算出参数μ、σ2，求得确定样本点对的类别后，可对非基准面匹配进行筛除，将基准面匹配用于影像配准.

两条剽悍大汉，把住牡丹池大门。左边的汉子一言不发，将手中锦缎包袱递给一旁的门童；右边的汉子同样一言不发，将一锭银子丢给另一个门童；这就表明，接下来的半天，这家浴池只接待一位客人，峋四爷。

1.3 投影差消除的影像配准

影像配准的关键是影像变换矩阵的解算，为保证变换矩阵的解算精度，需要准确的特征提取、精确的特征匹配、合理的特征匹配筛选. 通过上述基于贝叶斯决策的投影差消除方法，可获取合理的匹配筛选标准，用于影像变换的解算，提高影像配准的精度.本文投影差消除的影像配准方法流程如图2 所示.

首先对原始影像进行预处理，采用SURF 特征算子提取特征点.SURF 是SIFT 的改进，其思想总体上与SIFT 相似，但采取的方法与SIFT 不同.SURF 通过采取一系列的措施提高特征提取速度［7］，然后基于FLANN 进行特征点的快速初匹配，得到样本区和待匹配影像的初匹配特征点集.按照1.2 节所述方法，在样本区内，交互剔除错误的初匹配，并标记出基准平面区域，得到匹配的分类情况，用于后续的贝叶斯决策训练.

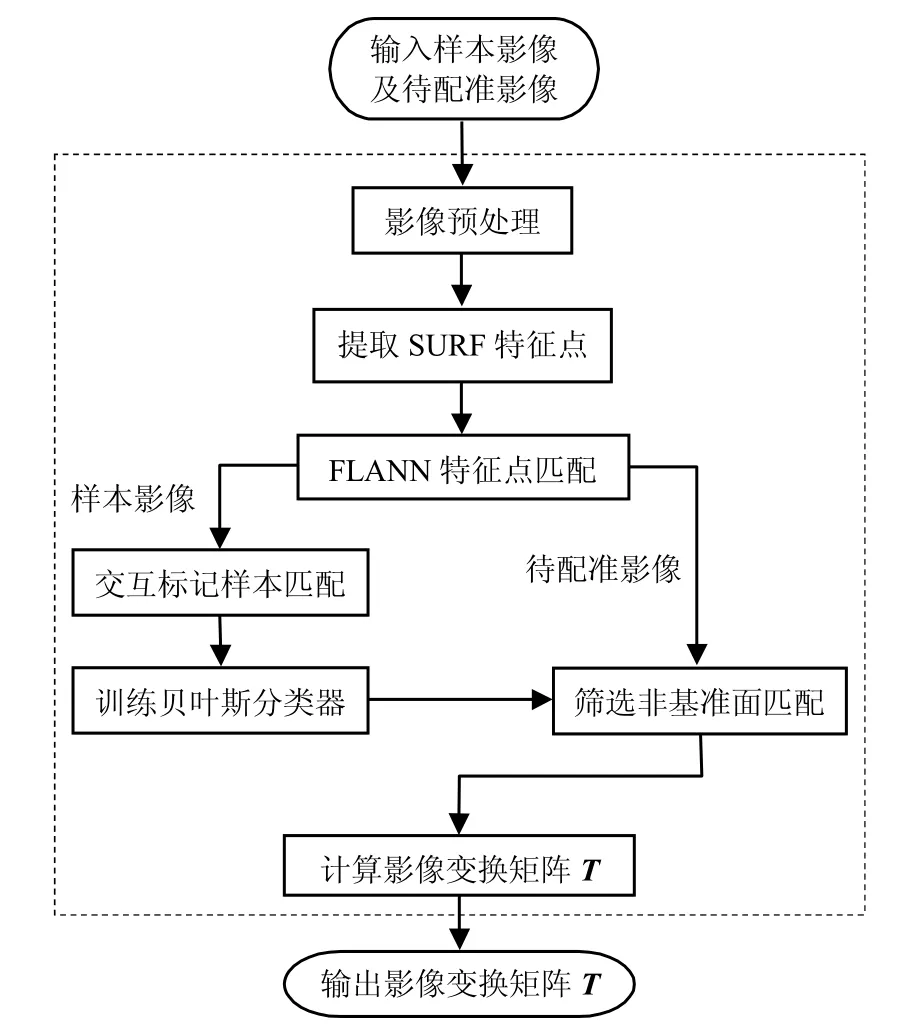
图2 本文投影差消除的影像配准方法流程Fig.2 Flowchart of the proposed method for eliminating projection difference

基于上述贝叶斯决策分类的特征点匹配筛选标准，对待匹配影像的初匹配特征点集进行筛选，消除非基准平面匹配，用于后续的影像间变换矩阵计算.航空影像应用中，在相机参数已知的情况下，摄影平台的移动及三轴扰动会导致影像的平移、缩放、旋转、斜切变形，因此在匹配特征点集基础上，本文采用透视变换矩阵T，并进行最小二乘方法求解，得到影像间的变换，采用坐标反算、重采样的方法得到配准后影像.

2 实验及讨论

2.1 实验数据及评价指标

实验选用KIT AIS 数据集作为实验数据.该数据集空间分辨率约为0. 15 m，由德国宇航中心(DLR)采集，后经德国卡尔斯鲁厄理工学院(KIT)摄影测量与遥感研究所(IPF)处理，并用于车辆轨迹监测、行人监测等研究.

KIT AIS 数据集已进行过初步校正，像点投影差依然存在，且由于地物起伏较大，影像之间地物像点投影差变化依旧明显，影响全局运动估计及影像配准.如图3 所示，KIT AIS 数据中的慕尼黑高速路立交桥路段，该区域立交桥存在两个高程平面且移位明显，像点投影差在不同摄站点航片上表现突出.实验面向车辆监测应用，取车辆所在高速路高程面为影像配准基准平面，若匹配特征点集中包含立交桥区域的非基准平面特征点，将导致影像配准质量下降.

为验证影像配准的效果，除了影像视觉效果外，本文还采用信息熵作为评价指标［17］. 一般地，较好的影像配准，影像差分结果的影像灰度复杂度较低，如果灰度值接近于0，则对应的信息熵较小，反之，信息熵越大说明影像的配准效果越差. 因此用信息熵来衡量影像配准效果是可行的.

图3 实验区示意Fig.3 Experimental area

2.2 实验结果与讨论

图4 贝叶斯分类训练Fig.4 Bayes classification training

实验采用卡方检验的方法分析像点投影差变化的分布特性.首先在基准平面和非基准平面上筛选一定数量的匹配特征点，并使用Whistler 盒图方法去除离群点，去除离群点后ω1余219、ω2余458;在取显著性水平α=0.05 的情况下下，基准平面与非基准平面内像点投影差变化的正态分布卡方检验的P-值分别为0. 09、0. 12，均大于α =0.05，可以认为像点投影差变化服从正态分布.

然后计算ω1、ω2区域内投影差变化的概率密度分布，对ω1、ω2区域概率密度分布进行正态分布拟合(见图5(a));按照1.2 节原理后验概率分布曲线交点C 即为判定标准，如图5(b)所示为C=(4.37 ×0.15 m，0.5).

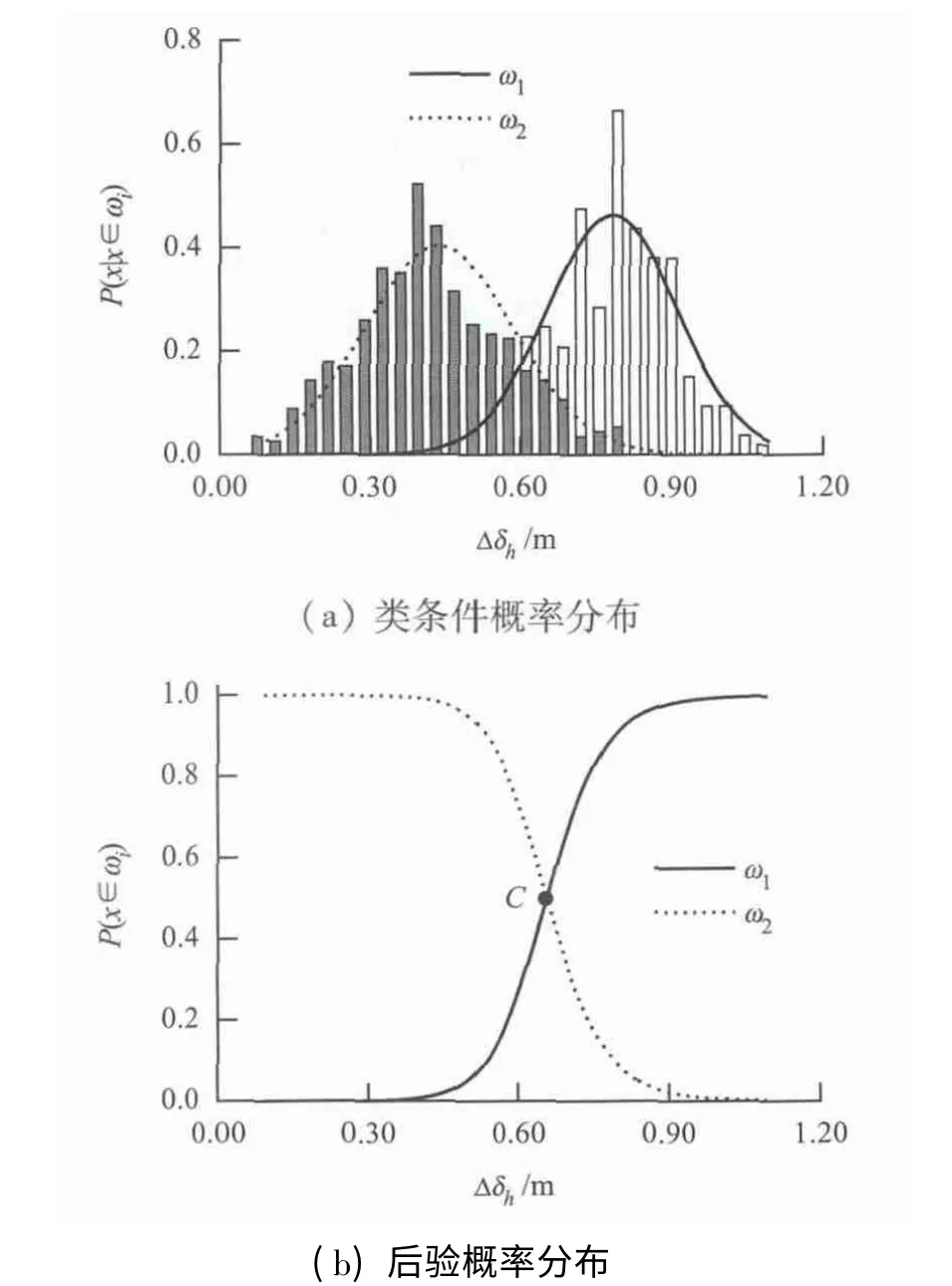
图5 类条件概率与后验概率分布Fig.5 Conditional probability and posterior probability distribution

进一步地，为验证方法的有效性，使用实验区同一批数据中的起、止2 张影像(像点投影差变化最大)，对比进行投影差消除和不进行投影差消除两种情况下的影像配准效果，待配准影像(图3 中Img-2)校正结果如图6 所示，监测平面(即地面主干道路区)差分结果如图7 所示.

对应的变换矩阵T 及信息熵H 见表1.

由图7 差分影像和表1 结果可知，经过投影差消除后，视觉上基准平面(即道路区域)影像配准效果得以改善，道路白线差分后基本全部消失. 从影像的熵变化来看，基准平面区域A、B、C内消除后的影像的信息熵较消除前减小约10%.

此外，由变换矩阵T 可以看出，其前后差异主要在影像变换的平移分量，与图6 影像的校正结果一致，这也是非基准平面匹配导致影像配准的主要误差.

图6 影像校正结果(Img-2)Fig.6 Image correction results

图7 差分影像结果Fig.7 Difference images

综上所述，本文基于贝叶斯决策的投影差消除方法，可以有效地提高影像配准精度，改善配准效果.

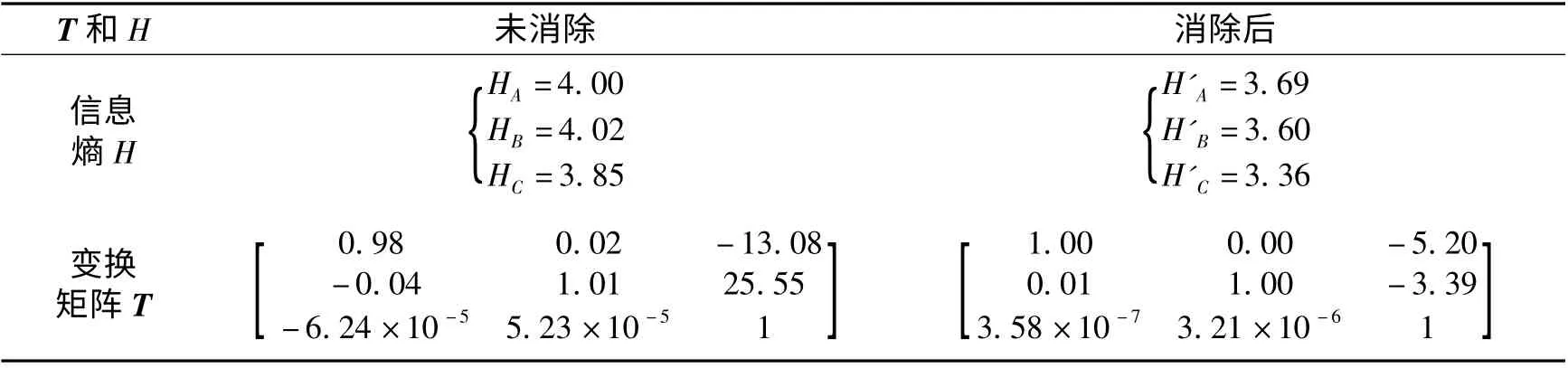
表1 实验结果Tab.1 Experimental results

3 结 论

本文针对像点投影差对影像配准精度的影响，提出了一种基于贝叶斯决策理论的像点投影差消除方法.采用设置样本区训练的方式，获取像点投影差变化规律，从而消除地形起伏对特征点匹配的影响，提高影像全局运动估计的精度. 实验选用KIT AIS 数据作为实验数据，以影像配准差分视觉效果和信息熵为评价指标，通过对比分析投影差消除前后影像配准精度，得出以下结论:

(1)相邻像对上同一视平面的像点投影差变化呈正态随机分布.

(2)基于贝叶斯决策理论的像点投影差消除方法，在使不同视平面匹配具有最大后验概率的准则下，可获得不同视平面匹配的决策规则，将其应用于同一研究区的其他影像配准能够获得较好的配准效果.

［1］ 刘承平，袁飞. 一种基于飞行平台的数字稳像及目标跟踪系统［J］. 中国电子科学研究院学报，2012，7(4):380-384.LIU Chengping，YUAN Fei. Flying platform based digital stabilization and target tracking system［J］.Journal of China Academy of Electronics and Information Technology，2012，7(4):380-384.

［2］ ZITOVA B，FLUSSER J. Image registration methods:a survey［J］. Image and Vision Computing， 2003，21(11):977-1000.

［3］ KIM J， FESSLER J A. Intensity-based image registration using robust correlation coefficients［J］.IEEE Transactions on Medical Imaging， 2004，23(11):1430-1444.

［4］ MTIR I H，KAANICHE K，CHTOUROU M，et al.Aerial sequence registration for vehicle detection［C］∥The 9th International Multi-conference on Systems，Signals and Devices (SSD). Chemnitz:IEEE，2012:1-6.

［5］ OLSON C F，ANSAR A I，Padgett C W. Robust registration of aerial image sequences［C］∥The 5th International Symposium on Advances in Visual Computing. Las Vegas:Springer，2009:325-334.

［6］ LOWE D G. Distinctive image features from scaleinvariant keypoints［J］. International Journal of Computer Vision，2004，60(2):91-110.

［7］ BAY H，TUYTELAARS T，Van GOOL L. Surf:speeded up robust features［C］∥Proceedings of the 9th European Conference on Computer Vision. Graz:Springer，2006:404-417.

［8］ CRIMINISI A，REID I，ZISSERMAN A. A plane measuring device［J］. Image and Vision Computing，1999，17(8):625-634.

［9］ FISCHLER M A，BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography［J］.Communications of the ACM，1981，24(6):381-395.

［10］ STONE H S，ORCHARD M T，CHANG E，et al. A fast direct Fourier-based algorithm for subpixel registration of images［J］. IEEE Transactions on Geoscience and Remote Sensing，2001，39 (10):2235-2243.

［11］ WOLBERG G，ZOKAI S. Robust image registration using log-polar transform［C］∥Proceedings of 2000 International Conference on Image Processing.Vancouver:IEEE，2000，1:493-496.

［12］ REDMILL K A，MARTIN J I，OZGUNER U. Aerial image registration incorporating GPS/IMU data［C/OL］∥Proceedings of SPIE，Evolutionary and Bio-Inspired Computation:Theory and Applications III ［2013-08-10］. http://spie. org/Publications/Proceedings/Paper/10.1117/12.820201.

［13］ 刘慧，李清泉，曾喆，等. 利用低空视频检测道路车辆［J］. 武汉大学学报:信息科学版，2011，36(3):316-320.LIU Hui，LI Qingquan，ZENG Zhe，et al. Vehicle detection in low altitude aircraft video［J］. Geomatics and Information Science of Wuhan University，2011，36(3):316-320.

［14］ 何敬，李永树，李歆，等. 基于点特征和边缘特征的无人机影像配准方法［J］. 西南交通大学学报，2012，47(6):955-961.HE Jing，LI Yongshu，LI Xin，et al. Registration method for unmanned aerial vehicle images based on point feature and edge feature［J］. Journal of Southwest Jiaotong University，2012，47(6):955-961.

［15］ SCHMIDT F. Tracking vehicles in aerial image sequences［EB/OL］. (2012-11-15)［2013-09-01］.http://www. ipf. kit. edu/english/downloads _ 707.php.

［16］ OZUYSAL M，CALONDER M，LEPETIT V，et al.Fast keypoint recognition using random ferns［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(3):448-461.

［17］ 高振宇，杨晓梅，龚剑明，等. 图像复杂度描述方法研究［J］. 中国图象图形学报，2010，15(1):129-135.GAO Zhenyu，YANG Xiaomei，GONG Jianming，et al. Research on image complexity description methods［J］. Journal of Image and Graphics，2010，15(1):129-135.