基于中点弦测模型的无砟轨道精调量迭代求解

魏 晖， 朱洪涛， 赵国堂， 万 坚， 王志勇

(1. 南昌大学机电工程学院，江西 南昌330031;2. 江西科技学院汽车工程学院，江西 南昌330098;3. 中国铁路总公司，北京100844)

轨道结构的组合性和所承受列车荷载的随机性与重复性，决定了即便是无砟轨道，其在运营过程中也不可避免地会出现残余变形积累，从而形成轨道的各种不平顺［1］. 轨道不平顺是轮轨系统的激扰源，是引起机车车辆振动和轮轨动作用力的主要原因，对列车行车的安全性、平稳性、舒适性、车辆和轨道部件的寿命以及环境噪声等都有很大影响［2］.在高速条件下，平顺性对行车的安全性、舒适性影响更突出. 因此，高速铁路必须具备高平顺性，其高低、轨向等平顺性指标均应控制在±2 mm以内［3］.如何实现高速铁路无砟轨道的高平顺性，涉及到包括设计、施工、养护等的全面质量控制，并隐含于控制标准、测量技术、量值传递以及施工工艺等一系列具体问题中.

现有的无砟轨道平顺性控制，基本上是通过对外部几何参数的绝对测量获得轨道工程坐标，然后用坐标法进行调整规划，进而调整扣件系统，以获得轨道的高平顺性. 坐标法的核心在于，通过轨道的外部几何参数控制轨道的内部几何参数，即通过轨道横、垂向偏差的调整实现轨道的高平顺性. 基于绝对测量的坐标法，其原理解析且结果闭合. 另外，坐标法以轨道外部几何参数为控制对象，故其应用于轨道施工，有利于轨道状态的全面均衡. 然而，在现场轨道养护中，该技术存在适用性的问题，具体表现在测量效率与轨道养护模式不匹配，测量精度与质量管理要求不统一，测量成果与平顺性概念不兼容.

我国相对测量历经近10 年的发展，目前已较为成熟，已广泛应用于轨道的日常检测. 在线下工程竣工后，为保证列车运营的安全性、舒适性，轨道管理的重点在于其平顺性控制［2］. 因此，有必要研究基于平顺性的轨道养护方案. 为不失一般性，本文的讨论仅限于轨道平面的平顺性.

1 相对测量技术及既有轨道整正算法

1.1 基于轨向平顺性的相对测量技术

目前用于高速铁路无砟轨道的0 级轨道检查仪，基本上采用惯性法进行测量，其原理是利用光纤陀螺(FOG)的Sagnac 效应［4］. 光纤陀螺利用光纤构成Sagnac 干涉仪，光路中顺、逆时针两束光波的相位差ΔΦ 与陀螺仪的转向角φ 的关系为

式中:N 为光纤匝数;λ 为真空中光波长;c 为真空中光速;A 为光路所包含的面积;t0～t 为积分时间.

在此基础上，再通过对转向角的里程积分，可得轨道的惯性轨迹序列，并可计算轨道不平顺(中点矢距)序列n-1}［5］.

由于相对测量技术采用惯性基准，故测量序列不包含外部几何尺寸信息，但测量效率可达4 ～8 km/h.

1.2 相对测量精度的要求

对轨道不平顺的精确测定是轨道整正的前提和基础，参照文献［6］关于测量仪器示值误差符合性评定的基本要求，测量允差U95与平顺性控制允差UMPEV间应满足

在此条件下，由测量允差引入的不确定度不会显著影响测量结果.根据文献［3］，轨向、正矢与高低控制值均为±2 mm，可得轨向、正矢测量允差U95=0.7 mm.

1.3 现行平顺性整正算法

传统的轨道平面整正算法应用于普速铁路，主要包括绳正法、偏角法及目穿法等，其中绳正法和偏角法是基于渐开线模型计算轨道调整量［1］. 设轨道等步距测量n 个桩点，得到实测中点矢距vi，并有设计中点矢距Vi，i =1，2，…，n -1. 假定轨道任意一点均沿渐开线移动且移动前后轨道长度不变，则有

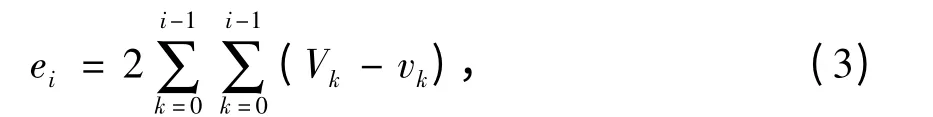
式中:ei为第i 点的调整量，i=1，2，…，n-1.

由于渐开线模型计算中存在累和计算［7］，意味着随里程增加，误差将不断增大，难以保证长撬平顺性，甚至产生“鹅头”或反弯.

目穿法则是目测不平顺，然后通过多次动道，逐点改善轨道的平顺性.此方法对不平顺的测定十分粗糙，且严重依赖于操作者的技能和经验，易破坏设计线型，故目前不能作为一种独立的整道方法应用于高速铁路无砟轨道精调.

2 基于轨向平顺性的轨道精调的基本思路

如前所述，采用陀螺仪可计算轨道的轨迹，但由于缺乏方位角及起算点的北东高(N，E，Z)坐标，且由于陀螺仪积分饱和，故直接计算轨道的坐标在工程上难以实现. 因此，直接对轨迹与轨道标准线型进行比较以获得整道量在技术上存在一定难度.然而，整道并非以全面恢复轨道几何尺寸为唯一目的，当以平顺性控制为目标时，则可避免求解积分常数，也可避免积分饱和对线型计算的影响.

从本质上讲，目穿法调轨过程可理解为一种迭代行为，即利用前几次的控制信息构成当前的输入控制信息，并按期望输出找到期望输入. 迭代算法具有严格的数学描述和定义，算法简单，且不依赖被控系统模型，对解决常规算法难以控制的复杂、不确定性系统有独到之处.

2.1 不平顺向量模型的建立

根据文献［8］，静态轨向、高低不平顺等的定义往往采用中点弦测(mid-chord offset，MCO)模型(图1).以平面为例，设测弦基长为L，并令轨道检查仪以步距0.5L 连续测量轨道，则轨道平顺性可表示为

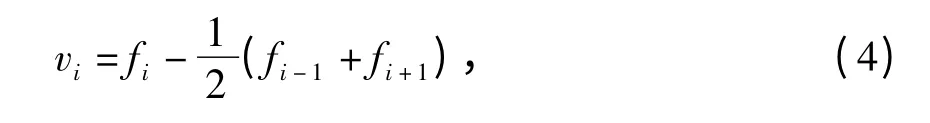
式中:vi为轨道不平顺，mm;fi(i=1，2，…，n -1)为轨道平面轨迹(横向偏差)，mm.

图1 轨道不平顺的中点弦测模型Fig.1 MCO model for track irregularities

由式(4)可知，中点弦测模型具有二阶差分的形式，即其直接表征轨道里程方向的二阶导数或曲率.中点弦测模型的主要问题是，其幅值增益将随不平顺波长变化而在0 ～2 间振荡［9-10］.然而，考虑到其相频特性无畸变，且有利于提取敏感波段的不平顺信息，故仍广泛用于轨道平顺性检查.

将轨道不平顺序列和轨道平面轨迹序列写成向量形式:

V=(v0，v1，v2，…，vn-1)T，

F=(f0，f1，f2，…，fn-1)T.

由式(4)，设

显然，A 为三对角矩阵，则式(4)写为

式(5)表达了轨向不平顺与轨道平面轨迹的关系.若V 为轨道设计参数确定的不平顺期望值，则轨道整正问题转化为通过初始轨迹向量F(0)求解期望轨迹输入F*的问题.

为便于说明，可对矩阵A 进行分解，令D 为单位矩阵，

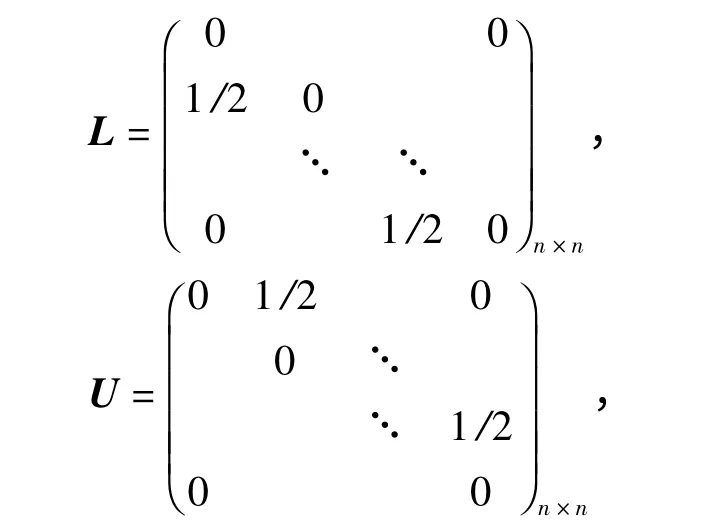
则

由 于A 的 顺 序 主 子 式Δi＞0 且为A 的元素，i=1，2，…，n)，故此时矩阵A 正定对称且对角占优.

2.2 轨道平面整正的迭代算法

式(5)的常规数值解法有直接法和迭代法，直接法(如Gauss 消去法)对原始数据误差和计算舍入误差敏感，故宜采用迭代法求解. 迭代法是求解大型线性系统(特别是稀疏矩阵)的有效方法，具有存储空间小、程序简单等特点. 它是从某个初始向量x(0)出发，按一定的迭代格式产生向量序列{x(k)}，随着k 增大，x(k)将逐步逼近x.

基本迭代法包括Jacobi 迭代、Gauss-Seidel 迭代以及超松弛(SOR)迭代等算法.相对于Jacobi 迭代算法，由于Gauss-Seidel 迭代、SOR 迭代算法利用了x(k+1)1，x(k+1)2，…，x(k+1)i-1计算x(k+1)i，故收敛速度快，迭代矩阵构造也较简单［11］.

SOR 迭代式为

式中，ω 为松弛因子.

当ω=0 时，式(6)即为Gauss-Seidel 迭代.

对式(5)进行迭代求解，须满足收敛性条件.另外，ω 的取值也直接影响收敛速度，一般采用试凑法寻优.

对于如矩阵A 的正定对称的三对角矩阵，根据文献［11］，当0 ＜ω ＜2 时，SOR 迭代收敛，且有最优松弛因子［12-13］

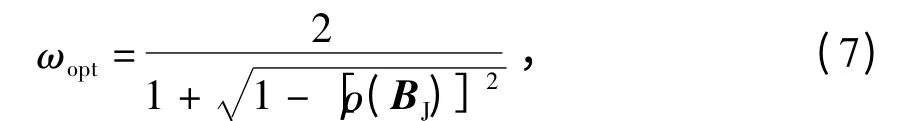
式中:ρ(·)为迭代矩阵的谱半径;BJ为式(5)的Jacobi 迭代矩阵.

则其特征值

当矩阵规模n 较大时，BJ的谱半径

由式(7)，最优松弛因子

此时，整理式(6)，有

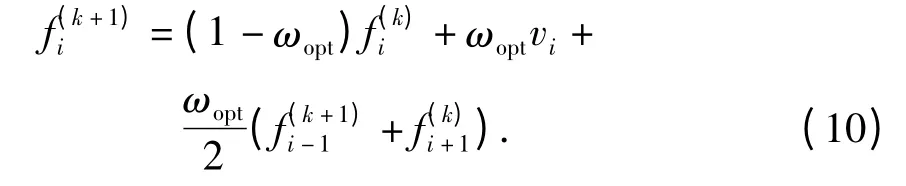
迭代终止条件:

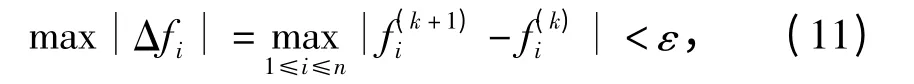
式中，ε 为精调允差，mm.

为使迭代计算的截断误差不致显著影响轨道的平顺状态，ε 应不大于作业验收标准的1/3.令为式(10)的精确解，则第i 点的调整量

2.3 迭代收敛速度及无砟轨道初始不平顺

式(10)对任意初始向量F(0)均收敛，然而其应用于工程计算需满足一定收敛速度的要求.收敛速度可用式(10)第k 次迭代的残差表示［11］:

对于正定对称的三对角矩阵，当ωopt=2(n +1)/(n+1 +π)时，有［13］

4.效力上，强调审前程序的约束性。由于目前的审前程序仅仅是一种程序性的准备，所有的内容都是在形式意义上存在的，因审前程序未完成而影响庭审的情况非常少见，反之，因为庭审程序而要求审前程序的重新开始却是普遍现象，这就导致审前程序毫无约束力可言。因此，民事审前程序的二元性价值改造需要对审前程序的效力进行特别的强调，在审前程序的目的没有实现的情况下，庭审程序不能任意开始。这样，既消除了诉讼程序的反复性和非约束性，强化了诉讼程序的安定性和可预测性，也提高了诉讼程序的有序性和效率性。

随矩阵规模增大，式(10)的迭代收敛速度降低，但保持收敛.当n =100 时，经过37 次迭代，误差约为初始值的10%.

另外，由式(13)，初始输入向量F(0)越接近期望输入向量F*，收敛速度越快. 对于轨道平面整正而言，即意味着当轨道初始平顺性较好时，上述算法可迅速逼近精确值，从而得到相应的调整量.

考察无砟轨道的初始平顺性，在钢轨定尺为100 m 的条件下，无砟轨道的初始不平顺主要源自轨道板的制造、安装及扣件系统误差. 综合《高速铁路工程测量规范》、《客运专线无砟轨道铁路工程施工技术指南》以及《福斯罗300-1 扣件系统零部件制造验收技术条件》等标准要求，并假定公差符合均匀分布，其他误差符合正态分布，在各项误差相互独立的条件下，标准不确定度［14］

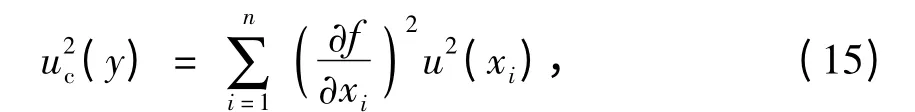
式中，u(xi)为误差xi的标准不确定度，i =1，2，…，n.

轨道的初始不平顺见表1.

表1 轨道初始不平顺Tab.1 Initial irregularities of ballastless track

从表1 可见，无砟轨道经过调板、锁定及轨道清理后，轨道的初始平顺性较好，仅需局部调整.这不仅有利于保证轨道的稳定性，也有利于整正量计算的快速收敛.

3 精调算法的现场试用

为验证基于平顺性的轨道精调算法在轨道精调中的效果，于2010 年12 月在某高速铁路土建三标5 工区进行了现场规模试用［15］. 试用线路长5.25 km，全线为CRTSⅡ型轨道板、跨区间无缝线路，平面线形选择包括直线、缓和曲线和圆曲线.

作为对照，另有30.75 km 线路采用基于全站仪的绝对测量技术进行精调.精调效果通过动态检查评价，动态质量评定执行350 km/h 标准.表2 为线路不平顺动态质量的比较. 从表2 可见，2 种精调方法的整道效果相当，均满足无砟轨道精调的要求.

图2 右轨平面调整效果(局部)Fig.2 Adjustment effect of right alignment (enlarged view)

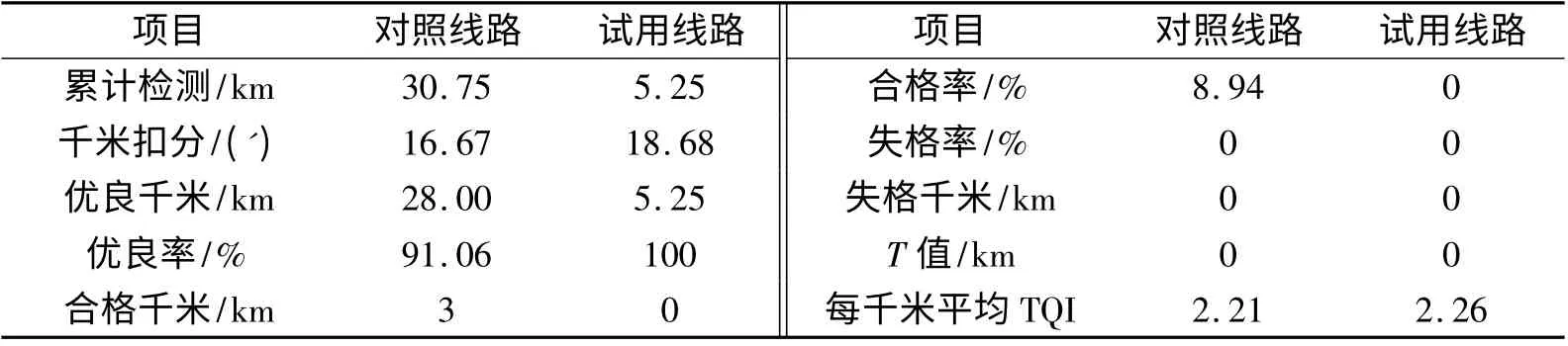
表2 线路不平顺动态质量比较Tab.2 Dynamic quality comparison of ballastless track

4 结 论

本文建立了轨道不平顺向量模型，提出了基于中点弦测模型的无砟轨道精调量计算方法和以恢复平顺性为目标的无砟轨道精调量逐次超松弛迭代算法，并且在某高速铁路进行了现场规模试用，获得以下结论:

(1)提出的算法具有收敛性，计算结果可以保证高速铁路无砟轨道的高平顺性，采用该算法不会显著改变轨道的外部几何尺寸.

(2)与已有的渐开线方法相比，由于无砟轨道精调量迭代算法是以轨道平顺性为期望输出对测量数据进行多次迭代，不存在累和问题和首尾控制条件，故可保证测量范围内的整体平顺;与基于绝对测量的坐标法相比，由于其输入输出均为轨道内部几何尺寸，故测量效率、解算效率及与既有养修规范的衔接等均优于坐标法.

(3)与绝对测量精调技术相比，提出的精调技术具有无需外部标志、测量环境适应性好、精调工作效率高等优点，作业效果与绝对测量精调技术相当，满足高速铁路无砟轨道养修的要求.

迭代算法的收敛性分析是在无干扰情况下进行的.但在长波条件下，测量数据存在各类扰动，需对算法的鲁棒性进行研究. 此外，当矩阵规模较大时，算法的复杂度将增加，需进一步研究迭代的加速算法，如进行分块迭代等.

［1］ 郝瀛. 铁道工程［M］. 北京:中国铁道出版社，2000:152-169.

［2］ 罗林，张格明，吴旺青，等. 轮轨系统轨道平顺状态的控制［M］. 北京:中国铁道出版社，2006:264-283.

［3］ 铁道部建设管理司. TB 10621—2009 高速铁路设计规范(试行)［S］. 北京:中国铁道出版社，2009.

［4］ LEE B. Review of the present status of optical fiber sensors［J］. Optical Fiber Technology，2003，9(2):57-79.

［5］ WEI Hui，ZHU Hongtao，WANG Zhiyong，et al.Center line coordinates survey for existing railway by 3-D constraints method［J］. Indonesian Journal of Electrical Engineering，2013，11(5):2816-2821.

［6］ 全国法制计量技术委员会. JJF 1094—2002 测量仪器特性评定［S］. 北京:中国计量出版社，2002.

［7］ 魏晖，吴仕凤，朱洪涛. 基于相对测量调轨的高铁有砟线路整道技术研究［J］. 铁道标准设计，2013(8):11-15.WEI Hui，WU Shifeng，ZHU Hongtao. Engineering trial of relative measuring adjustment method for HSR ballast rail maintenance［J］. Railway Standard Design，2013(8):11-15.

［8］ 铁道部运输局. TG/GW115—2012 高速铁路无砟轨道线路维修规则(试行)［S］. 北京:中国铁道出版社，2012.

［9］ AHMADIM M. Filtering effects of mid-chord offset measurements on track geometry data［C］∥Proceedings of the 1999 ASME/IEEE Joint Railroad Conference.［S.l.］:IEEE，1999:157-161.

［10］ 魏晖，朱洪涛，万坚. 基于中点弦测法的矢距计算通式及其特性研究［J］. 铁道工程学报，2013(11):40-44.WEI Hui，ZHU Hongtao，WAN Jian. A universal algorithm for bias-chord offset based on MCO and its characteristics analyses［J］. Journal of Railway Engineering Society，2013(11):40-44.

［11］ VARGA R S. 矩阵迭代分析［M］. 蒋尔雄，游兆永，张玉德，译. 上海:上海科技出版社，1966:52-121.

［12］ HAGEMAN L A，YOUNG D M. Applied iterative methods［M］. New York:Academic Press，1981:46-121.

［13］ 关治，陈景良. 数值计算方法［M］. 北京:清华大学出版社，1990:406-422.

［14］ 全国法制计量技术委员会. JJF 1059—1999 测量不确定度评定与表示［S］. 北京:中国计量出版社，1999.

［15］ 京沪高速铁路股份有限公司. 关于印发《〈高速铁路无砟轨道快速测量精调技术研究〉成果审查意见》的通知［Z］. 北京:京沪高速铁路股份有限公司，2011.