基于累积前景理论的随机异质道路网配流模型

吕 彪， 刘海旭， 蒲 云，， 王恪铭， 郭 茜

(1. 西南交通大学峨眉校区，四川 峨眉山614202;2. 西南交通大学交通运输与物流学院，四川 成都610031)

城市道路交通系统受交通事故、恶劣气候条件等随机事件影响，引起需求的随机波动和路段通行能力的随机退化［1］，导致出行时间的不确定性. 目前，关于随机路网环境下交通分配问题的研究已引起研究者的广泛兴趣.文献［2］假定出行者以行程质量作为路径选择依据，建立了路段通行能力随机变化情况下基于行程质量的随机用户均衡模型.文献［3］提出了基于出行时间预算(travel time budget，TTB)的用户均衡模型，TTB 定义为在一定可靠度下，出行者完成出行需要预算的最短出行时间，可表述为路径期望出行时间与缓冲时间之和.文献［4］假定出行者以超预算期望出行时间(mean-excess travel time，METT)作为择路依据，建立了随机需求条件下的超预算期望交通均衡(mean-excess traffic equilibrium)模型. METT 定义为出行时间超过TTB 条件下的数学期望.文献［5-6］对文献［4］进行了扩展，同时考虑了需求与路段通行能力的随机变化，但忽视了路网拓扑关系对配流的影响.

上述研究工作［2-6］是基于期望效用理论(expected utility theory，EUT)或随机效用理论(random utility theory，RUT)，假定出行者的路径选择行为完全理性. 已有研究表明，在随机路网环境下，出行者的择路行为并非完全理性，而是存在明显的参考点依赖，呈现有限理性特征，符合累积前景理论(cumulative prospect theory，CPT)的决策框架［7-12］.

在基于CPT 的用户均衡问题研究中，参考点选择是关键问题. 在已有研究中，将参考点分为内生和外生两类.外生参考点通常是一个固定值，而内生参考点是一个变量，取决于网络状态［9］. 由于参考点的选择受决策情景、出行者性格特征等因素的影响，具有内生性，因此，选择内生参考点比较合理［10］.文献［10-11］将TTB 作为参考点，描述出行者对可靠性的关注. 文献［9］将METT 作为参考点，反映了出行者对出行可靠性和不可靠性两方面的关注.

已有的基于CPT 的用户均衡模型，一般都假定路网中的出行者是同质的，具有相同风险取向，基于某种单一准则设置参考点，这与现实情况不符.已有研究表明，在随机路网环境下，面对出行时间的随机波动，出行者的风险取向存在明显差异，路径选择行为也存在明显差异［13］.为简化问题，已有研究大多忽视了出行时间随机变化的具体致因，仅通过主观假定路段或路径出行时间的变异系数来反映其不确定程度［9，11］，或是仅考虑了供需条件某单一方面的随机变化［10-12］，在此条件下得到的网络均衡状态与实际情况存在较大偏差.

基于上述分析，本文对已有研究在下述两方面进行扩展:

(1)考虑用户异质性，按风险取向不同将出行者分为4 种类型，分别以可靠度低于50%的出行时间预算、期望出行时间、可靠度高于50%的出行时间预算及超预算期望出行时间作为选择路径的内生参考点.

(2)同时考虑需求与路段通行能力两方面的随机变化，调整不符合实际的假设，明确考虑出行者对出行时间的估计误差及路网拓扑关系等影响配流的重要因素，建立更符合现实条件的配流模型.

1 随机供需条件下的流量与出行时间

1.1 随机需求条件下的交通流量

考虑交通网络G =(N，A)，N 表示节点集合，A 表示路段集合，用W 表示OD(origin-destination)对集合，Rw表示OD 对w 的路径集合，w∈W.

假定由于各种随机事件影响，需求随机波动.令Qw表示OD 对w 的需求量，服从某种概率分布.由于假定需求为随机变量，因此，路径流量和路段流量也是随机变量. 根据需求量、路段流量及路径流量之间关系，可得:

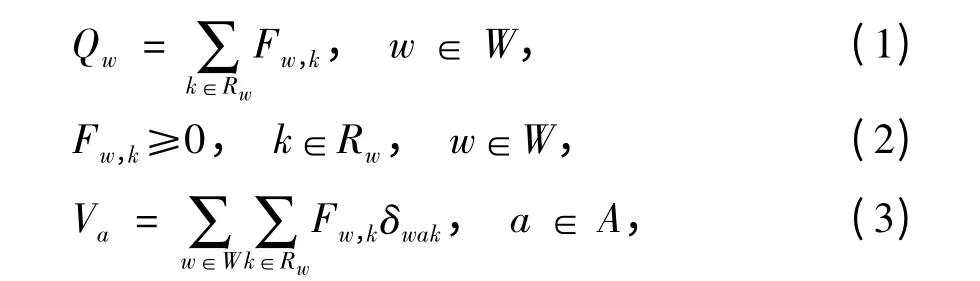
式中:Fw，k为OD 对w 路径k 的流量(随机变量);

Va为路段a 的流量(随机变量);

δwak为0-1 变量，如果OD 对w 的路径k 使用路段a，δwak=1，否则δwak=0.

设qw、fw，k和va分别表示Qw、Fw，k和Va的均值，根据式(1)～(3)，可得:

式中:E(·)为期望值算子.

为便于计算，假设［4］:

(1)路径流量与OD 需求服从相同的概率分布;

(2)路径流量的方差-均值比(variance-tomean rate，VMR)与对应OD 需求的方差-均值比相同.

令εQw和εFw，k分别表示Qw和Fw，k的方差，根据假定(1)和(2)可得:

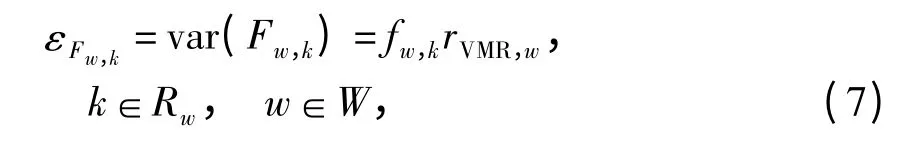
式中:var(·)表示方差算子;

rVMR，w=εQw/qw表示OD 对w 需求量的方差-均值比.

令εVa表示Va的方差，根据式(3)和(7)，可得:

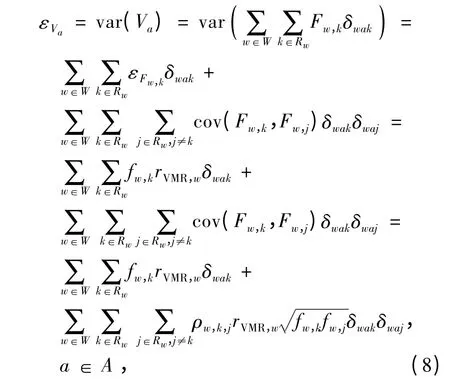
式中:cov(Fw，k，Fw，j)为Fw，k与Fw，j的协方差;

ρw，k，j为Fw，k与Fw，j的相关系数.

特别地，若假定路径流量相互独立，则εVa可简化为

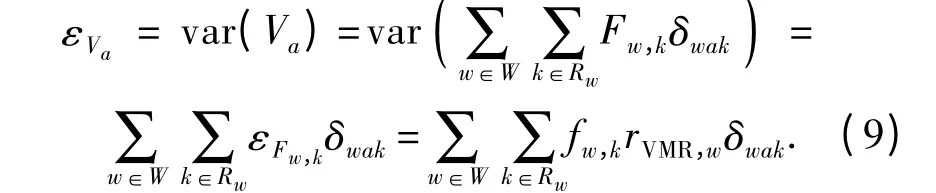
假定Qw服从参数为μQw和σQw的对数正态分布，则根据对数正态分布的性质，Qw的分布参数可根据其均值和方差进行如下估计:

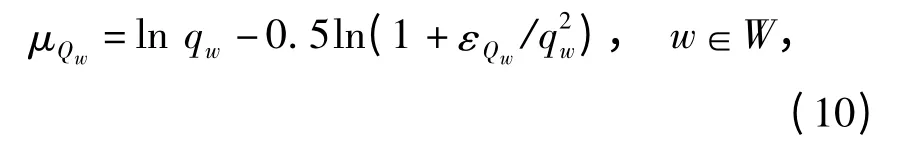
当需求服从对数正态分布时，根据前述假设，可知路径流量也服从对数正态分布. 令μFw，k和σFw，k表示Fw，k的对数正态分布参数，可得:

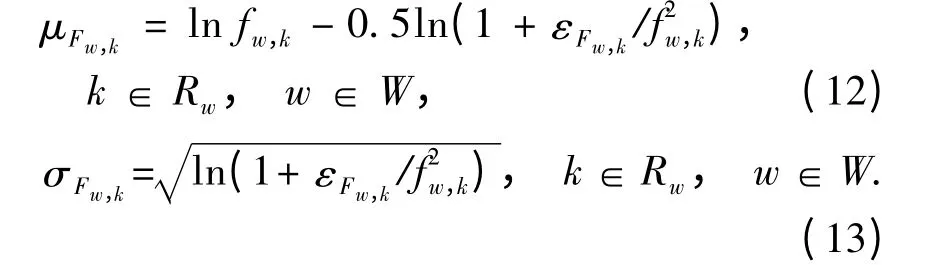
由于路径流量服从对数正态分布，而路段流量由路径流量叠加而成. 因此，根据文献［14］可知，对数正态随机变量之和近似服从对数正态分布，因此路段流量同样近似服从对数正态分布. 令μVa和σVa表示Va的对数正态分布参数，可得:

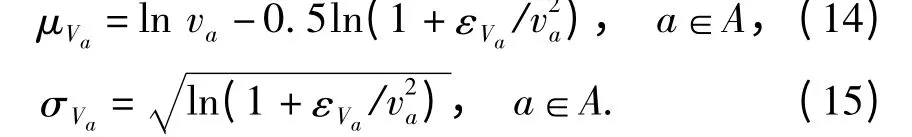
1.2 随机供需条件下的出行时间

假定路段出行时间用如下BPR(bureau of public roads)函数描述:

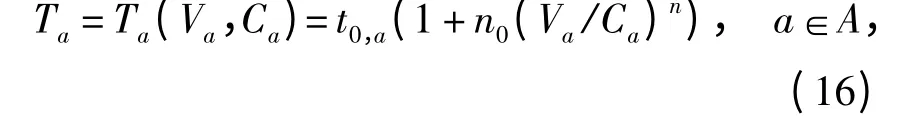
式中:Ta为路段a 的出行时间(随机变量);

t0，a为路段a 的自由流出行时间;

Ca为路段a 的通行能力，是随机变量;

n0和n 为BPR 函数参数.

造成需求波动和路段通行能力退化的原因一般不同，因此，与相似问题的研究［1］相同，假定Va与Ca相互独立.令ta和εTa分别表示Ta的均值和方差，根据式(16)有:

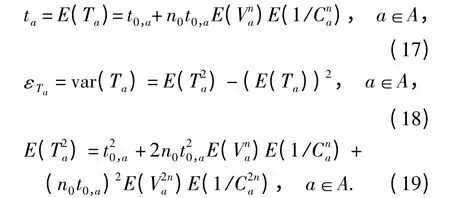
从式(17)～(19)可知，要计算ta和εTa，需先计算E(Vna)、E(V2na)、E(1/Cna)及E(1/C2na). 由于Va服从对数正态分布，可得:

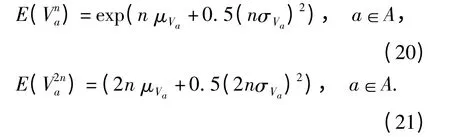
由于缺乏实测数据，与相似问题的研究［1，3］相同，假定Ca服从上界为设计通行能力cmax，a、下界为最低通行能力κacmax，a(κa表示能力退化系数，其值越小表示能力退化程度越高)的均匀分布.在此假定下，可得［1，3］:

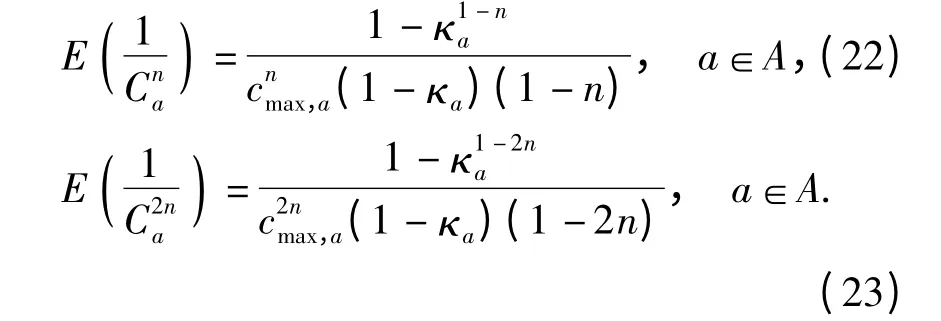
根据式(17)～(23)，可得:

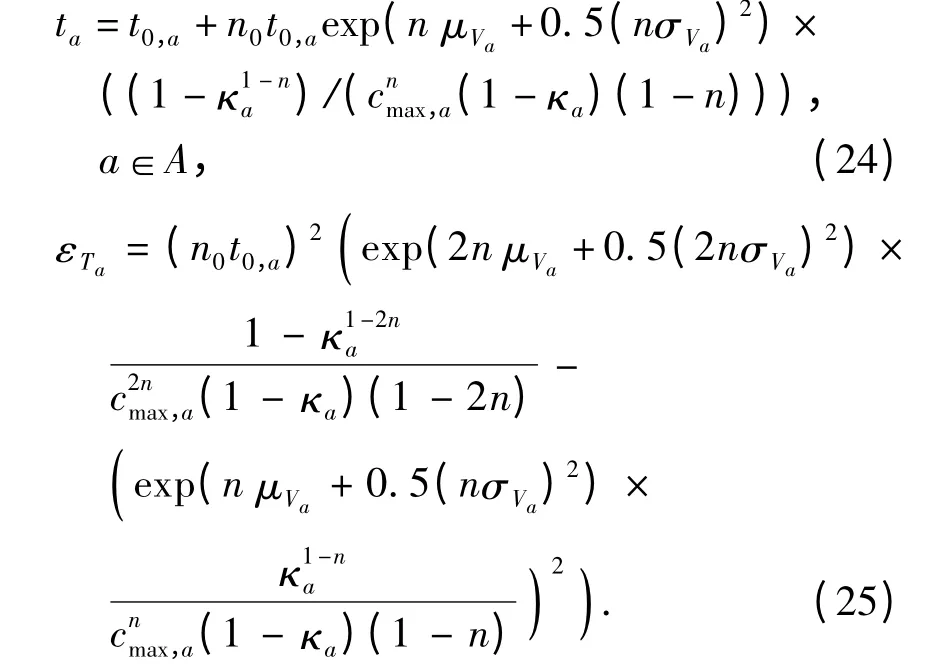
令Tw，k表示OD 对w 路径k 的出行时间.根据路段-路径关联关系可得:

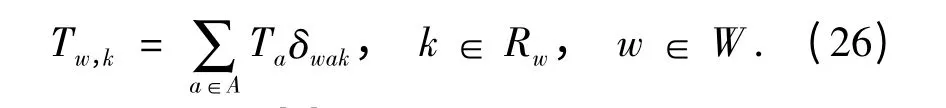
在已有研究［1-4］中，一般假定路段的出行时间相互独立，然而在实际中，由于路网拓扑关系，路段之间往往相互影响，各路段出行时间是相互关联的.

根据式(26)，Tw，k的均值tw，k和方差εTw，k可表示为

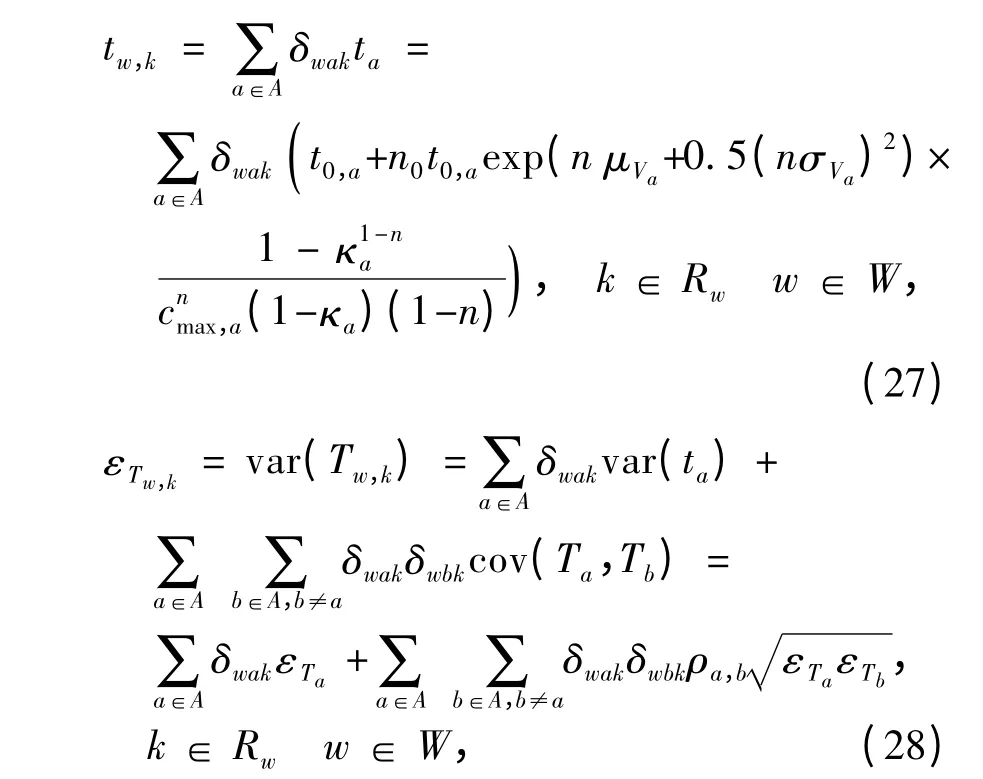
式中:cov(Ta，Tb)为Ta与Tb之间的协方差;

ρa，b表示Ta与Tb间的相关系数.

为方便计算，假定Tw，k服从正态分布，即

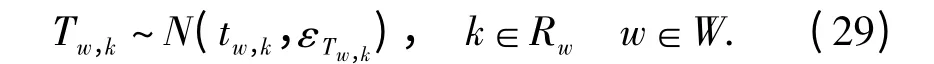
Tw，k的概率密度函数可表示为

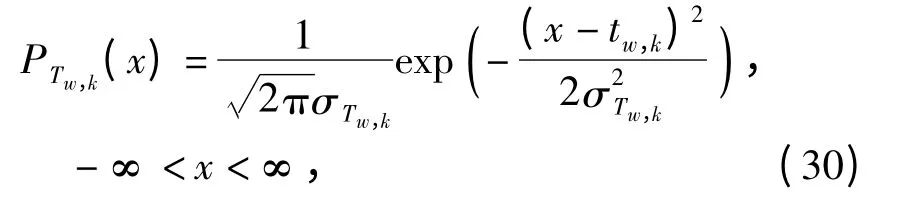
令ηw，k(ω)表示可靠度为ω 时的超预算期望出行时间，根据式(30)和文献［4］可得:

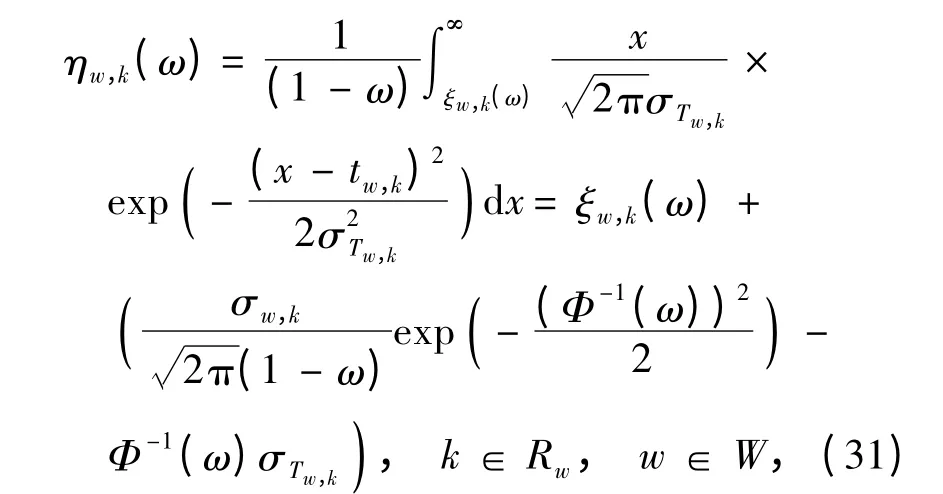
式中:ξw，k(ω)为可靠度ω 下的出行时间预算［1，3］，

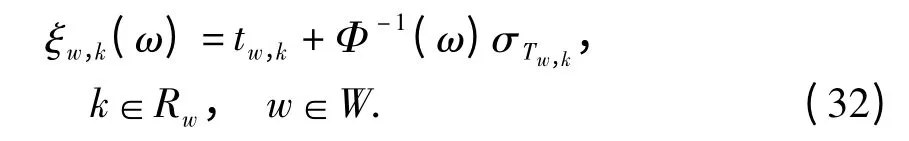
将式(32)代入式(31)可得:

2 基于CPT 的随机用户均衡模型

2.1 累积前景理论决策体系

累积前景理论决策体系包括价值函数、决策权重函数及前景值计算公式［7-12］. 根据累积前景理论，出行者选择路径的依据是路径前景，而前景值的计算依赖于价值函数与决策权重函数. 因此，要完成上述决策，首先要确定选择路径的参考点.

2.1.1 参考点选择

参考点是衡量收益或损失的尺度，参考点不同，路径前景以及网络均衡流量的分布形态也不同.不失一般性，假定路网中存在4 类出行者.令出行者类型集合M ={1，2，3，4}. 其中，第1 类出行者对风险持偏好态度，以可靠度低于50%的出行时间预算作为择路参考点;第2 类出行者对风险持中立态度，以期望出行时间作为择路参考点;第3类出行者对风险持保守态度，但仅考虑出行的可靠性，不考虑出行的不可靠性，以可靠度高于50%的出行时间预算作为择路参考点;第4 类出行者对风险持非常保守的态度，同时考虑出行的可靠性和不可靠性，以超预算期望出行时间作为择路参考点.

基于上述分析，各类出行者的参考点可分别由以下各式确定:

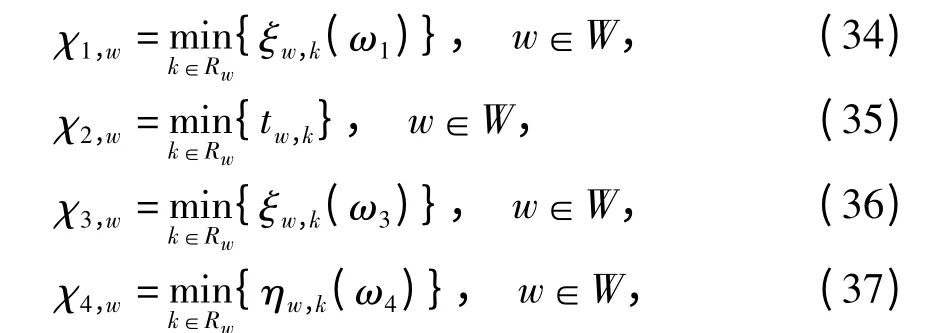
式中:χ1，w、χ2，w、χ3，w、χ4，w分别为第1 ～4 类出行者选择OD 对w 路径时的参考点;

ω1、ω3、ω4分别为第1、3、4 类出行者的可靠度需求.

2.1.2 价值函数

价值函数描述根据路径实际效用形成的主观效用，衡量偏离参考点的价值，即收益或损失.根据累积前景理论，价值函数可表示为

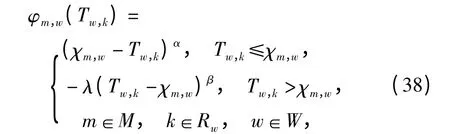
式中:φm，w(Tw，k)为第m 类出行者选择OD 对w 路径k 时的价值函数.

α 和β(0 ＜α，β≤1)均为风险敏感系数，值越大表示越敏感，其中，α 表示收益敏感系数，β 表示损失敏感系数;

λ(λ≥1)为损失规避系数，λ 越大表示决策者对损失比对相同收益的敏感程度越强.

当Tw，k低于χm，w时，对出行者意味着收益，而当Tw，k＞χm，w时，对出行者而言意味着损失.

2.1.3 决策权重函数

决策权重函数描述了出行者根据路径效用实际发生概率形成的主观发生概率.一个典型的决策权重函数如下:

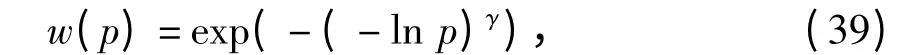
式中:p 和w(p)分别为实际概率和感知概率;

γ 为感知概率系数，参数γ 的取值范围为0 ＜γ≤1，γ 越小表明决策者对小概率事件的重视程度越高.

2.1.4 前景值计算

若已知Tw，k的分布，可根据价值函数和决策权重函数计算选择某条路径出行时的前景，

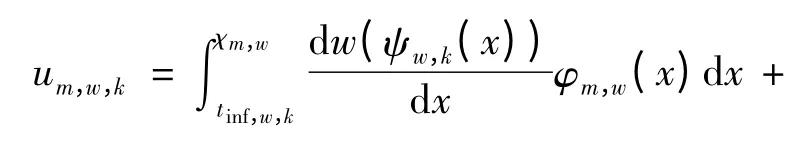
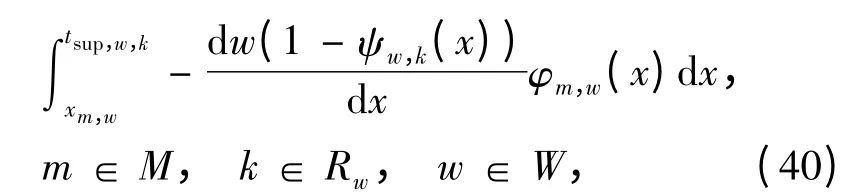
式中:um，w，k为第m 类出行者选择OD 对w 路径k出行时的前景;

ψw，k(·)为Tw，k的累积分布函数;

tsup，w，k和tinf，w，k分别为Tw，k取值的上下限.

2.2 基于CPT 的随机用户均衡模型

在实际路网中，出行者很难完全掌握出行时间的分布规律，从而可能导致对前景值的估计存在偏差.基于此，将出行者理解的路径前景值视为随机变量，由实际观测值和随机误差项两部分构成，可表述如下［15］:

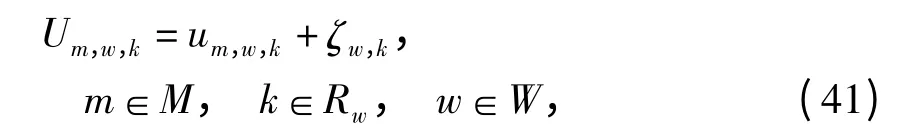
式中:Um，w，k为第m 类出行者对OD 对w 路径k 的理解前景值(随机变量);

ζw，k为出行者对OD 对w 路径k 前景值的估计误差.

若假定ζw，k为独立同分布的Gumbel 变量，且均值为0，则第m 类出行者选择OD 对w 路径k 的概率［15］为

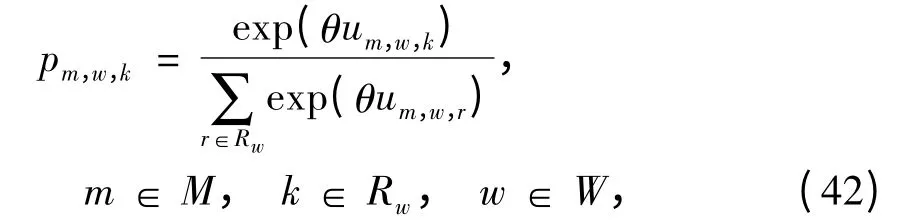
式中:θ 为估计误差参数，其大小与出行者对前景值的估计误差成反比.

假定出行者以估计路径前景值作为选择路径的依据.在择路过程中，出行者试图寻找估计前景值最大的路径出行，当出行者无法通过单方面改变路径而提高估计路径前景时，称网络达到了基于累积前景理论的随机用户均衡(cumulative prospect theory-based stochastic user equilibrium，CPT-SUE)状态.

根据随机用户均衡原理，CPT-SUE 模型的均衡条件［15］可表示为:

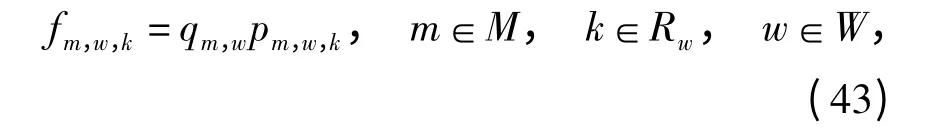
式中:qm，w为OD 对w 第m 类出行者的需求量;

fm，w，k为OD 对w 路径k 上第m 类出行者的流量.

式(43)表示的均衡条件可用下述等价的变分不等式模型描述.

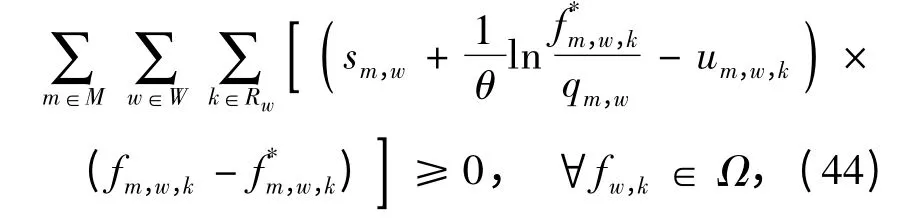
式中:带上标* 的量为变分不等式的解;

sm，w为第m 类出行者选择OD 对w 路径出行时的期望最大估计前景值［15］，

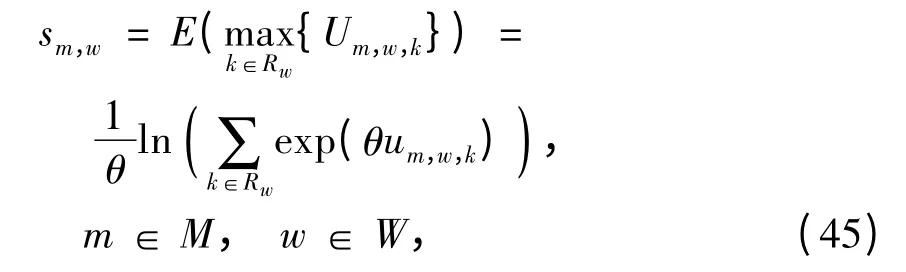
Ω 由下式确定，

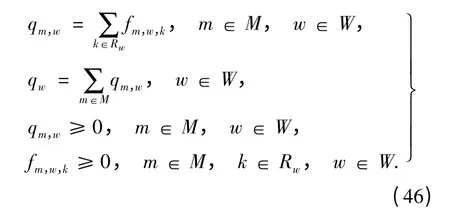
令f 表示由{fm，w，k，m∈M，k∈Rw，w∈W}组成的列向量，v(f)表示由组成的列向量. 由于v(f)关于f 连续，且可行集Ω 为有界闭凸集，根据文献［16］的推论2.2.6，式(44)和(46)表示的变分不等式至少存在一个解. 但因无法确保v(f)的单调性，因此，解的唯一性无法保证. 式(44)和(46)表示的变分不等式可使用相继平均法［15］(method of successive average)求解，算法步骤从略.

3 算例分析

测试网络为图1 所示的Nguyen and Dupuis 网络.该网络由4 个OD 对、13 个节点、19 条路段以及25 条路径组成. 路段上所标数字表示路段编号(自由流出行时间、设计通行能力).

在缺乏实测数据情况下，不失一般性和合理性，测试参数设置如下:

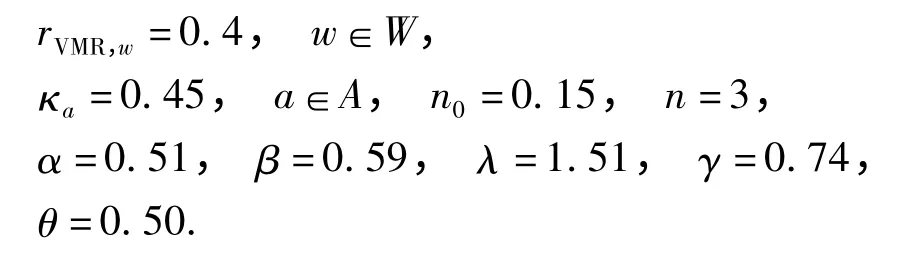
tinf，w，k取路径自由流出行时间，即

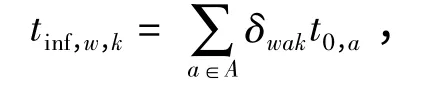
tsup，w，k取可靠度为99.999%时的出行时间预算值.为便于比较，令ω1=40%，ω3=ω4=85%.

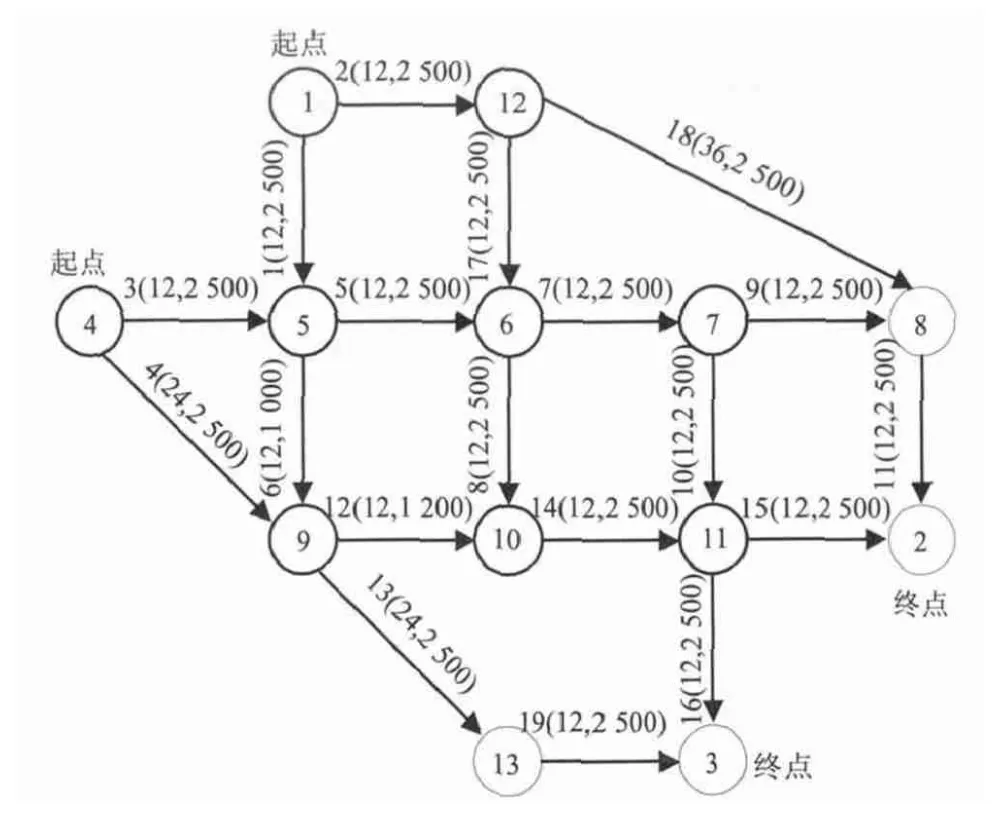
图1 Nguyen and Dupuis 测试网络Fig.1 Nguyen and Dupuis network

假定存在共用路段的路径之间流量相关系数为0.25，否则为0;假定存在邻接关系的路段之间的时间相关系数为0.25，否则为0.

将qm，w表示如下:

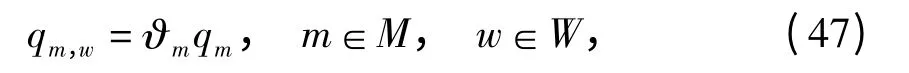
式中:ϑm为第m 类出行者需求占总需求的比例，令ϑ1=ϑ2=ϑ3=ϑ4=0.25，∑m∈Mϑm= 1;

qw为OD 对w 的总需求，令

q12=1 200 辆/h， q13=1 500 辆/h，

q42=1 000 辆/h， q43=800 辆/h.

限于篇幅，仅给出OD 对(1，3)上的结果. OD对(1，3)包含6 条路径，路径1 ～6 可分别用路段序列表示为:

2→17→7→10→16; 2→17→8→14→16;

1→5→7→10→16; 1→5→8→14→16;

1→6→13→19; 1→6→12→14→16.

表1 为测试网络的配流结果.根据表1 数据容易验证，对路网中每类出行者，其路径流量满足式(43)确定的均衡条件，表明配流结果正确有效.由于不同类型出行者选择路径的参考点不同，因此，对同一路径具有不同的出行前景和不同的选择概率.此外，从表2 中还可以发现，由于存在估计误差，使用的路径前景值并不相等.

图2 比较了CPT-SUE 模型与传统SUE 模型(假定出行者完全理性，分别以可靠度低于50%的出行时间预算、期望出行时间、可靠度高于50%的出行时间预算以及超预算期望出行时间作为选择路径的依据)的配流结果，从图2 可见，二者产生的均衡路径流量存在较大差异. 实证研究表明，在随机路网环境下出行者的择路行为呈有限理性，存在参考点依赖，用CPT-SUE 模型配流更符合实际，表明基于完全理性择路行为假设的用户均衡模型产生的配流结果与实际情况存在较大偏差.

表1 OD 对(1，3)上的配流结果Tab.1 Traffic assignment results for OD pair (1，3)

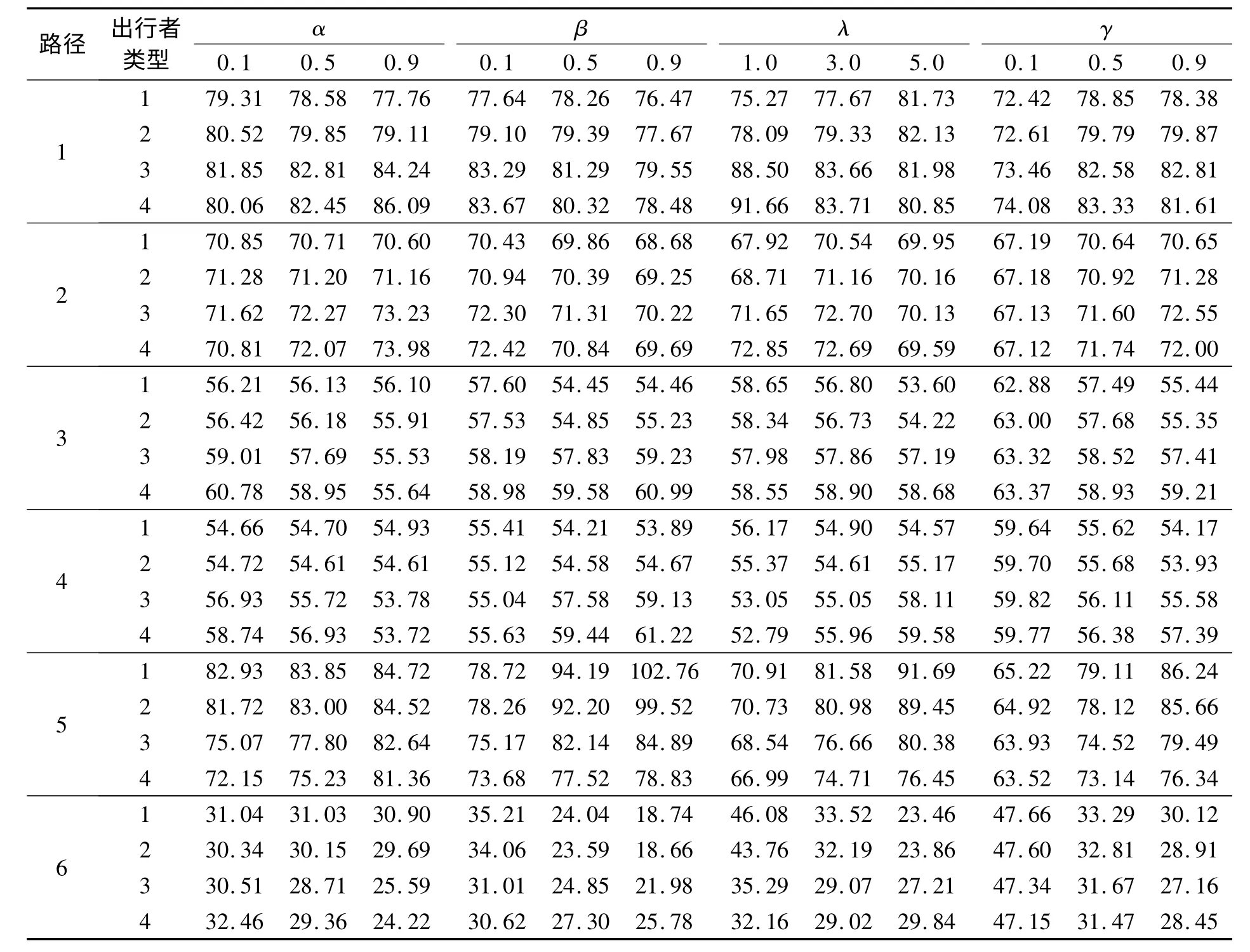
表2 参数α、β、λ 和γ 对均衡路径流量的影响Tab.2 Effects of parameters α，λ，β and γ on equilibrium route flows辆/h

图2 CPT-SUE 与传统SUE 的配流结果比较Fig.2 Comparisons of assignment results from the CPT-SUE model and the conventional SUE model

表2 给出了参数α、β、λ、γ 对配流结果的影响.从表2 数据可以看出，使用不同的参数值，将产生不同的均衡路径流量分布;同时，还可观察发现，参数取值变化对不同类型出行者的影响程度不同.

图3 ～6 给出4 类出行者因参数α、β、λ、γ 不同引起的路径前景值变化.

图3 参数α 对路径前景的影响Fig.3 Effects of parameter α on route prospects

从图3 可见，随着参数α 值的增大，所有类型出行者的路径前景均呈增大趋势，但第3、4 类出行者的变化比第1、2 类出行者更显著. 原因是α 取值越大，价值函数在收益区域(出行时间低于参考点区域)的边际敏感性递减程度越小，当出行时间低于参考点时，出行者可能获得更大收益;第1、2类出行者的参考点取值较小，使其获得收益的概率相对较小，而第3、4 类出行者参考点取值较大，使其获得收益的可能性相对较大.上述两方面原因产生了图3 所示结果.

从图4 可以看出，随着参数β 取值增大，所有类型出行者的路径前景均呈减小趋势，但第1、2 类出行者的变化比第3、4 类出行者更显著.原因是β取值越大，价值函数在损失区域(出行时间高于参考点区域)的边际敏感性递减程度越小，当出行时间高于参考点时出行者可能遭受更大的损失;同时，第1、2 类出行者的参考点取值较小，使其遭受损失的概率相对较高，而第3、4 类出行者参考点取值较大，使其遭受损失的概率相对较小. 上述两方面原因导致图4 所示结果.

图5 参数λ 对路径前景的影响Fig.5 Effects of parameter λ on route prospects

图6 参数γ 对路径前景的影响Fig.6 Effects of parameter γ on route prospects

从图5 可知，随着参数λ 取值增大，所有类型出行者的路径前景均呈减小趋势，但第1、2 类出行者的变化比第3、4 类出行者更显著.这是因为λ 取值越大表示出行者越重视损失，路径前景中损失部分所占比重会加大;同时，第1、2 类出行者的参考点取值较小，使其遭受损失的概率相对较高，而第3、4 类出行者参考点取值较大，使其遭受损失的概率相对较小.上述两方面原因导致图5 所示结果.

从图6 可知，随着参数γ 取值增大，第1、2 类出行者的路径前景呈减小趋势，而第3、4 类出行者的路径前景呈增大趋势. 这是因为γ 取值越大，表示出行者越重视大概率事件而忽视小概率事件，会增大大概率事件的决策权重而减少小概率事件的决策权重.第1、2 类出行者的参考点取值较小，出行者遭受损失属于大概率事件，而第3、4 类参考点取值较大，出行者获得收益属于大概率事件.因此，γ 取值越大，第1、2 类出行者损失部分的决策权重会增加，而第3、4 类出行者收益部分的决策权重会增大.上述两方面原因导致图6 所示结果.

由表2 和图3 ～6 可知，随着参数α、β、λ、γ 取值的变化，不同类型出行者的路径前景与均衡路径流量将发生不同变化，表明在交通分配中考虑出行者择路行为的有限理性和风险取向的差异性非常必要.

必须指出的是，本文得出的参数α、β、λ、γ 对配流的影响规律是基于特定参数设置和网络环境，并不一定具有普适性.

4 结束语

根据出行者择路行为的有限理性和风险取向差异性，建立了CPT-SUE 模型.算例结果表明:

(1)CPT-SUE 模型和基于完全理性择路行为假设的配流模型产生的均衡路径流量存在明显差异.实证研究表明，在随机路网环境下出行者择路行为呈有限理性，因此，使用CPT-SUE 模型配流更符合实际，基于完全理性择路行为假设的配流模型产生的结果可能与实际情况存在较大偏差.

(2)累积前景理论参数设置对配流具有重要影响.随着参数α 取值增大，所有类型出行者的路径前景均呈增大趋势，但第3、4 类出行者比第1、2类出行者的变化更显著;随着参数β 和λ 取值增大，所有类型出行者的路径前景均呈减少趋势，但第1、2 类出行者比第3、4 类出行者变化更显著;随着参数γ 取值增大，第1、2 类出行者的路径前景呈减小趋势，而第3、4 类出行者的路径前景呈增大趋势.研究表明，在交通分配中考虑出行者择路行为的有限理性和风险取向差异性是非常必要的.

(3)需要指出的是，前景理论并非完全成熟的理论，不能完全取代期望效用理论或随机效用理论.首先，应用前景理论研究交通配流问题需要考虑是否适合所处的交通环境，一般说来，当出行者面临的出行环境具有较大不确定性时，运用前景理论进行配流比较合理. 其次，前景理论的参数取值和参考点选取均依赖调查或实验数据支撑，根据决策环境合理确定参数α、β、λ 和γ 的取值，是下一步深入研究的问题.

［1］ SIU B W Y，LO H K. Doubly uncertain transportation network: degradablecapacityandstochastic demand［J］. European Journal of Operational Research，2008，191(1):166-181.

［2］ 刘海旭，蒲云. 基于行程质量的随机用户平衡分配模型［J］. 中国公路学报，2004，17(4):93-95，118.LIU Haixu，PU Yun. Stochastic user equilibrium assignment model based on travel trait［J］. China Journal of Highway and Transport，2004，17(4):93-95，118.

［3］ LO H K，LUO X W，SIU B W Y. Degradable transport network: travel time budget of travelers with heterogeneousriskaversion［J］.Transportation Research Part B，2006，40(9):792-806.

［4］ CHEN A，ZHOU Z. The α-reliable mean-excess traffic equilibrium model with stochastic travel times［J］.Transportation Research Part B，2010，44(4):493-513.

［5］ 吕彪，蒲云，刘海旭. 供需不确定条件下的预算-超额用户平衡模型［J］. 中国公路学报，2012，25(2):113-120.LÜ Biao，PU Yun，LIU Haixu. Budget-excess user equilibrium model under uncertain supply and uncertain demand［J］. China Journal of Highway and Transport，2012，25(2):113-120.

［6］ 吕彪，蒲云，刘海旭. 多用户类型弹性需求随机期望-超额用户平衡模型［J］. 西南交通大学学报，2012，47(3):516-525.LÜ Biao，PU Yun，LIU Haixu. Stochastic mean-excess user equilibrium model with multiple classes and elastic demand［J］. Journal of Southwest Jiaotong University，2012，47(3):516-525.

［7］ AVINERI E，PRASHKER J N. Sensitivity to travel time variability: travelers'learningperspective［J］.Transportation Research Part C，2005，13(2):157-183.

［8］ CONNORS R D，SUMALEE A. A network equilibrium model with travelers' perception of stochastic travel times［J］. Transportation Research Part B，2009，43(6):614-624.

［9］ 王伟，孙会君. 基于内生参考点的交通网络均衡模型［J］. 应用数学和力学，2013，34(2):190-198.WANG Wei，SUN Huijun. Traffic network equilibrium model based on endogenous reference point［J］.Applied Mathematics Mechanics，2013，34(2):190-198.

［10］ XU H L，LOU Y Y，YIN Y F，et al. A prospectbased user equilibrium model with endogenous reference points and its application in congestion pricing［J］. Transportation Research Part B，2011，45(2):311-328.

［11］ 张波，隽志才，林徐勋. 基于累积前景理论的随机用户均衡交通分配模型［J］. 西南交通大学学报，2011，46(5):868-874.ZHANG Bo，JUAN Zhicai，LIN Xuxun. Stochastic user equilibrium model based on cumulative prospect［J］. Journal of Southwest Jiaotong University，2011，46(5):868-874.

［12］ 王倩，周晶，徐薇. 基于累积前景理论考虑路网通行能力退化的用户均衡模型［J］. 系统工程:理论与实践，2013，33(6):1563-1569.WANG Qian， ZHOU Jing， XU Wei. A user equilibrium model based on the cumulative prospect theory for a degradable transport network［J］. Systems Engineering:Theory and Practice，2013，33 (6):1563-1569.

［13］ 史峰，罗端高. 降级路网的多类用户均衡分配模型及求解算法［J］. 交通运输系统工程与信息，2008，8(4):70-76.SHI Feng， LUO Duangao. Model and solution algorithm for multiclass user equilibrium assignment problem in a degradable road network［J］. Journal of Transportation Systems Engineering and Information Technology，2008，8(4):70-76.

［14］ FENTON L F. The sum of log-normal probability distributions in scatter transmission systems［J］. IEEE Transactions on Communications Systems， 1960，8(1):57-67.

［15］ 黄海军. 城市交通网络平衡分析:理论与实践［M］.北京:人民交通出版社，1994:179-248.

［16］ FACCHINEI F，PANG J S. Finite-dimensional variational inequalities and complementarity problems［M］. New York:Springer，2003:145-154.