主动配电网的两阶段优化调度模型

庄慧敏， 肖 建

(1. 成都信息工程大学控制工程学院，四川 成都610225;2. 西南交通大学电气工程学院，四川 成都610031)

分布式发电(distributed generation，DG)技术，尤其是可再生能源(renewable energy sources，RES)的发展可以优化能源结构，提升绿色能源利用率，推动节能减排和实现经济可持续发展［1］. 近年来，配电网中DG 的渗透率迅速增长，传统配电网正逐步演变为具有众多可调可控资源(可调DG、储能装置、柔性负荷等)的主动配电网.主动配电网的优化调度策略是主动配电网对可控资源实施主动管理的核心技术，也是实现网络安全经济运行的重要手段［2］.

目前，对含风力发电的电力系统调度及微网优化调度的研究［3-4］比较多，而对主动配电网的优化调度研究较少.

现有的主动配电网优化调度模型按目标函数可以分为配电网运行成本最小［5-6］、电力公司效益最大［7-8］、社会综合效益最大［9］.文献［6］以整个调度周期内配电网运行成本最低为目标函数，以可控分布式能源及联络开关作为控制手段，实现主动配电网的优化调度. 在文献［6］的目标函数中，将联络开关的状态作为控制变量，达到优化网络结构的目的，但没有给出发电功率关于该状态量的具体表达式，在实施方面存在一定的困难. 文献［7］在主动配电网的调度模型中考虑了输电和高压配电网网损的影响，以电力公司效益最大化为目标，得到了区域电网中含分布式电源的主动配电网优化调度模型，并得出效益最大时分布式电源对主动型配电网的最佳渗透率.

在调度对象方面，大多以DG 为主体，部分文献包括了储能装置，少数文献［10］以可控负荷为主体.目前考虑需求响应的优化调度策略成为研究热点［11-12］.文献［12］针对微网的分布式发电调度，提出了考虑实时电价、可中断负荷等需求侧响应策略的分布式发电协调优化调度模型.

通过对主动配电网优化调度的研究现状可以看出，目前的调度策略存在以下问题:

(1)多数研究只考虑了日前调度策略，没有考虑RES 发电预测及负荷预测的偏差对调度策略的影响;

(2)主要集中于DG 的有功功率优化，而没有考虑DG 作为无功资源对电网的辅助服务作用;

(3)没有考虑DG 在配电网中引起的过压问题，过压可能会触发保护装置将其从电网切除，浪费电网资源和可再生能源.

基于上述问题，本文提出主动配电网两阶段优化调度策略:日前优化调度和日内滚动修正两阶段调度.日前经济调度模型以一个完整调度周期内的配电网运行成本最低为目标函数，以可调度DG、可控负荷作为控制手段，同时确保储能系统在整个调度周期的能量守恒及容量约束;而日内滚动修正以日前调度计划为基础，以DG 的有功消减量和无功功率作为控制变量，每小时根据最新的短期预测信息更新日前调度值，从而优化网络电压，降低网络损耗，提高DG 并网能力. 最后，通过扩展的IEEE34 节点配电网算例对本文建立的模型进行了验算.

1 日前调度建模

主动配电网的日前调度模型是对次日可调分布式能源(发电机、储能系统)有功功率及响应负荷减载量、减载时段的计划.因此，主动配电网优化调度的控制向量可以表示为

控制向量的前Ng个分量是可控分布式发电单元的输出功率，中间Ns个分量是储能单元的充放电功率，最后的Nl个分量是响应负荷的减载量.本文选取可减载负荷模型作为需求响应模型.主动配电网可在负荷高峰时段与用户签订负荷减载合同，并给予补偿.

1.1 目标函数

将目标函数F 定义为整个调度周期内主动配电网的运行成本最小.运行成本包括分布式发电机的发电成本、从关口购电的成本以及补偿需求响应的成本.

式中:t 为时段编号;

T 为调度周期的总时段数，对于每个阶段可认为各DG 单元功率、储能单元功率以及负荷大小不变;

Δt 为单位阶段的时长;

Ng为可调DG 单元总数;

g 为可调DG 编号;

Nl为响应负荷总数;

l 为可控负荷编号;

Cg(t)和PDGg(t)分别为第g 个可调DG 单元在时段t 的单位发电成本和有功功率;

Cl(t)和PRSl(t)分别为第l 个响应负荷在时段t 的减载补偿价和减载量;

PEX(t)和CEX(t)分别为配变关口的交换功率及其电价.

该目标函数从本质上能反映出优化调度分布式能源、储能充放电策略及需求响应策略合理化带来的收益.一般来说，分布式能源发电成本优于电网，在负荷一定的情况下，分布式发电利用率越高，电网输送电能就越少，目标函数的值就越小.此外，储能系统或需求响应的优化调度可以实现削峰填谷带来的峰谷电价差收益，并且响应用户还会因此获取一定的补偿，也可以使目标函数值变小.

1.2 约束条件

主动配电网优化调度的约束条件除了常规的潮流平衡方程、节点电压上下限约束、支路功率最大限制约束之外，还包括如下约束:

(1)功率平衡

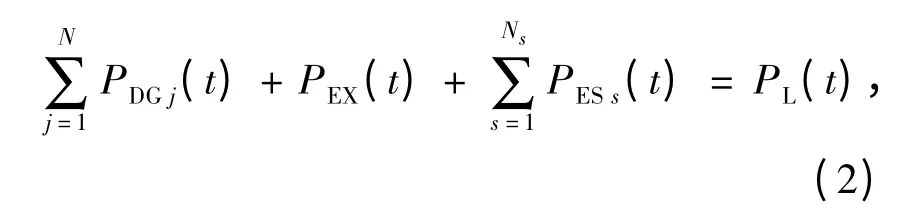
式中:N 为所有DG 单元个数;

PL(t)为时段t 的总负荷功率.

(2)储能单元能量守恒

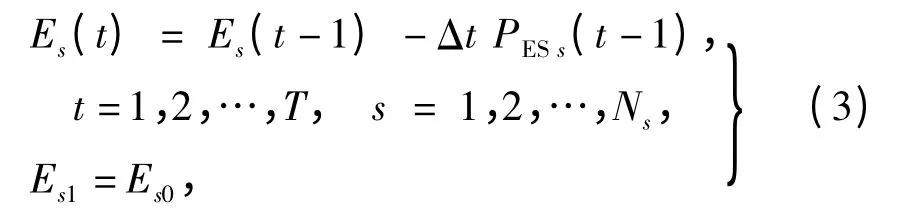
式中:

Es0和Es1为第0 和1 个储能单元在时段t 的剩余能量.

(3)发电单元及储能单元的功率和能量限制

式中:

Pmax，DGj为第j 个分布式发电单元的功率上限值(对于风力发电或光伏发电为预测值);

Pmin，ESs(小于0)、Pmax，ESs、Emin，s、Emax，s分别为第s 个储能单元充放电功率的下限值和上限值、剩余能量的最小允许值和最大允许值.

(4)需求响应负荷的减载量限制

式中:

Pmin，RSl、Pmax，RSl分别为第l 个需求响应负荷的减载量下限值和上限值.

(5)配变关口功率约束

为了减小主动配电网的功率波动对输电网的影响，需考虑配电网根节点的关口交换功率约束，即

本文建立的优化调度模型与传统模型的区别主要在于:将储能单元及需求响应用于抑制可再生能源功率的波动，提高系统运行的经济性. 所建立的模型是复杂的混合整数规划问题.

2 日内优化调度模型

由于RES 发电预测及负荷预测都受其自身不确定性的影响，因此在配电网的实际运行中，可能会出现节点电压越限的情况. 此外，当配电网出现意外事故(例如某支路断线)时还可能导致某支路过流等异常现象.因此，为了保证配电网安全、可靠和经济地运行，还需在日前优化调度的基础上进行日内优化调度.

日内优化调度模型是根据最新的短期预测信息和负荷需求等，对日前调度计划进行滚动调整.在滚动修正阶段，由于更接近实际情况，并且合理地消减可控DG 的发电量、鼓励DG 向配电网提供无功支持，可改善电压问题、提高大规模DG 的消纳能力［13］.因此，引入可控DG 有功功率消减量及向配电网提供的无功功率，既考虑了系统运行的经济性，又从数学角度把消减量和无功输出作为松弛变量，保证模型存在可行解.

日内优化调度的启动周期一般为30 ～60 min，本文取调度周期为1 h，即每小时执行一次.调度过程为:收集配电网系统信息(网络状态信息、可再生能源短期平均功率预测值和负荷需求预测值)，然后计算三相潮流，若发现有技术条件约束不能满足(例如节点电压越限等)，则启动日内优化调度程序，修正参与网络电压控制的分布式发电单元的有功功率和无功功率输出.

2.1 目标函数

在DG 稳态运行时采用PQ 类型. DG 通过电力电子装置或常规旋转电机接口并网，且其并网功率已能实现有功无功分别独立调节［14］.

考虑到有载调压变压器(on-load tap changers，OLTC)分接头不应频繁调整，本文假设在日内优化的实时控制时段内，OLTC 分接头固定. 当配电网运行过程中出现过压或支路功率越限等异常情况时，可通过消减可控DG 的有功功率和控制其无功输出进行缓解或消除异常情况.

日内优化调度具有实时性，因此模型的控制变量不宜过多，目标主要偏向于系统的经济性. 在日内优化调度中，配电网将对支持优化调度的发电单元给予一定的补偿.为此，目标函数J 考虑主动配电网的调度成本(包括DG 消减有功功率的成本CGC和提供无功支持的成本CQ)及能量损耗成本CLOS，即

(1)消减有功功率成本

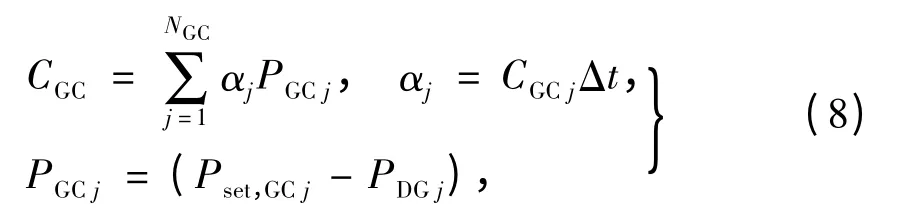
式中:

NGC为可消减有功功率的DG 个数;

CGCj为第j 个DG 消减单位电量(1 kW·h)的成本;

Pset，DGj为可调DG 的日前优化调度值，对于不可调DG(例如风力或光伏发电单元)为发电功率预测值;

PDGj为第j 个DG 的控制目标值;

PGCj为第j 个DG 的有功功率消减值.

(2)提供无功支持成本

式中:

NQ为可向配电网提供无功支持的DG 个数;

Qk和CQk分别为第k 个DG 输出的无功功率和提供单位无功量(1 kVar·h)的成本.

(3)能量损耗成本

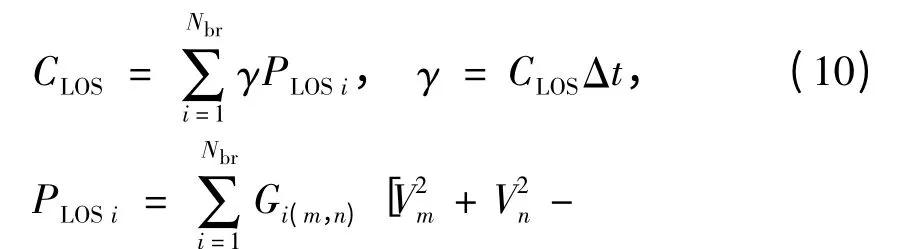
式中:CLOS为单位能量损耗成本;

PLOSi为第i 条支路损失的有功功率;

Nbr为配电网支路总数;

Gi(m，n)为连接节点m 和n 的支路i 的电导;V 和θ 分别为节点的电压幅值和相位.

消减有功功率是一种比较昂贵的控制手段，通常只在电网安全受到威胁时采用. 因此，其控制成本取较大值.

2.2 约束条件

约束条件除了日前优化调度模型的约束外，还包括如下约束:

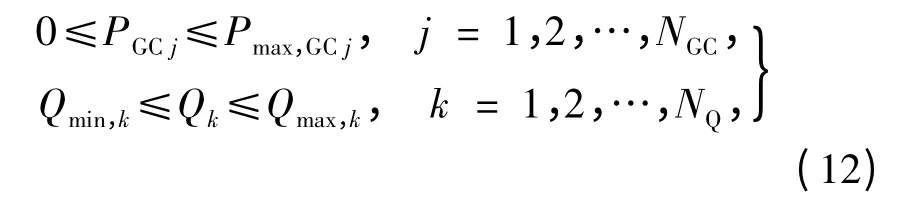
式中:

Pmax，GCj为第j 个DG 的最大允许消减量;

Qmax，k、Qmin，k分别为第k 个DG 的最大、最小无功率.

本文提出的两阶段调度优化模型是一个混合整数规划模型，可采用优化规划软件CPLEX 对其求解.考虑到本文的日内调度中需要计算配电网潮流，用Matlab 编写了线性规划模型的混合整数规划优化模型求解程序，而配电网模型建立及日内调度的潮流计算则由软件PSCAD/EMTDC 执行，两个软件的接口程序采用C+ +语言编写.

3 算例分析

3.1 算例

以扩展的IEEE34 节点配电网为算例进行分析.测试网络结构如图1 所示.

图1 IEEE34 节点测试系统Fig.1 IEEE34-node test system

该系统包含33 条支路，辐射运行，电压等级为24.9 kV，最大负荷总功率为7 500 kW，可中断负荷为1 000 kW.配电网节点802、812、818 各连接一台燃气轮机(gas turbine，GT)，节点856 与一台柴油(diesel，DE)发电机相连，相关的发电功率极限和发电成本单价见表1. 两个不可调的光伏(photovoltaic，PV)发电单元分别和配电网节点844、826 相连，峰值容量均为500 kW，节点842、824 各连接一个储能装置(energy storage source，ESS)(ESS842、ESS824)，充放电功率上限均为120 kW，电量上限均为600 kW·h，充放电效率均为0.95.其他网络和负荷参数见文献［15］.

表1 可调DERs 的模型参数Tab.1 Model parameters of the dispatchable DERs

该算例以一天24 h 为一个完整调度周期，调度间隔为1 h，配变关口的市场电价采用阶梯电价(如图 2 所示)，可中断负荷的补偿价为0.9 元/(kW·h).

图2 市场电价Fig.2 Market electrical price

为了分析简便，两个PV 单元采用相同的光照曲线，全天的有功功率预测见图3. 图3 中的功率值为相对于最大功率的标幺值.

3.2 日前调度结果

用程序计算出测试系统各调度单元全天的最优有功功率如图4 所示.

由图4 看出，DG 的总功率特性与负荷特性基本保持一致，当负荷较大时DG 的总功率较大，负荷较小时总功率较小.而从配电网关口的购电量则与负荷成反比趋势，即在荷峰时段从关口购电量最小，在荷谷时段从关口购电量较大. 此外，GT、DE的功率特性和可中断负荷的响应特性主要是由根节点关口的实时电价决定的，在峰时期间电价成本较高，GT、DE 基本都处于满发状态;在荷谷时段电价成本较低，GT、DE 功率为其最小值;在最高峰期间，电价成本高于可中断负荷的补偿价，可中断负荷供电.

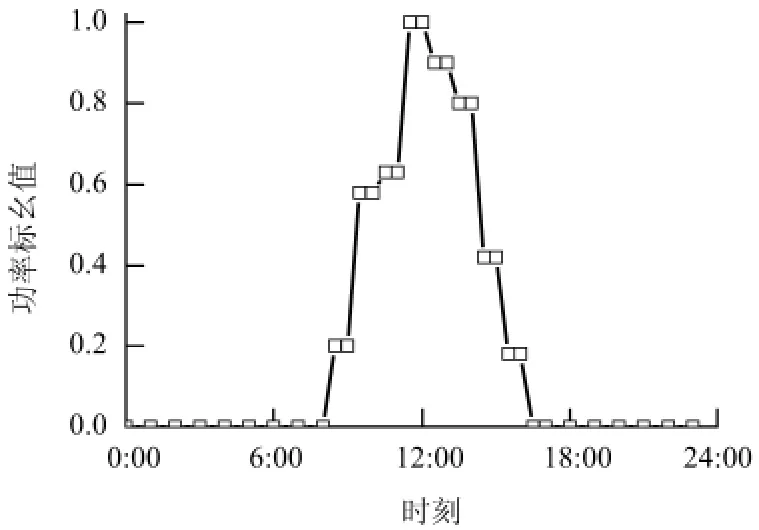
图3 光伏发电的有功功率预测Fig.3 Forecasted active power outputs of photovoltaic generation

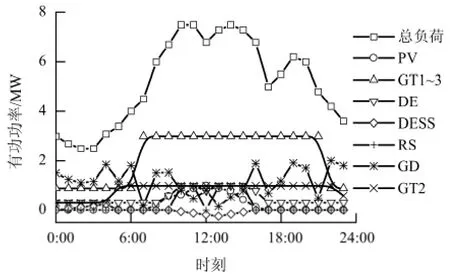
图4 日前调度结果Fig.4 Day-ahead scheduling solution

通过图4 还发现，储能单元的充放电策略通过优化计算也得到了合理的分配:在负荷最低谷期间(1:00 ～5:00)处于充电状态，在负荷最高峰期间进行(9:00 ～14:00)放电，在其他时间(负荷平稳期间)充放电功率为0.

因此，通过对主动配电网各可控单元的优化调度，不仅能够减少配电网的运行成本，还可对大电网起到积极的削峰填谷作用.

3.3 日内调度结果

取系数

α=1.5 元/(kW·h)，

β=γ=0.7 元/(kW·h).

GT 和DE 的初始功率因数素均为0.85. 为验证日内优化调度策略的有效性，以负荷的低谷(2:00 ～3:00)与高峰(10:00 ～11:00)两个典型时段为例.

经优化计算得到这两个时段的GT 和DE 的有功消减量及无功输出，见表2 和表3. 荷谷时段的网络损耗由日内优化前负荷功率的3. 32%降为3.11%，而荷峰时段由3.24%降为3.02%.此时全天运行成本为40 926.19 元，较未采用优化调度时的运行成本42 309. 72 元，运行成本降低了3.27%.

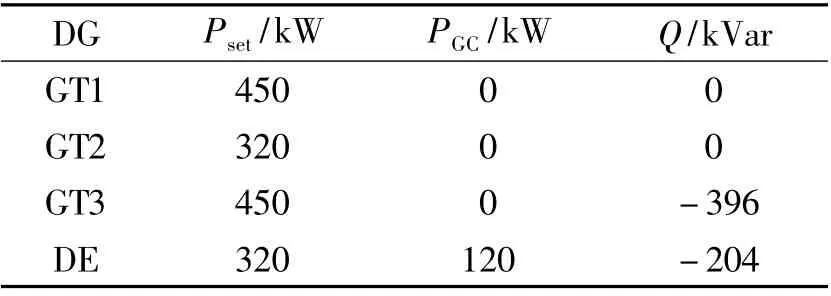
表2 荷谷时段日内优化结果Tab.2 Intra-day solution in load trough period

表3 荷峰时段日内优化结果Tab.3 Intra-day solution in load peak period

由表2 可看出，荷谷时段的GT1、GT2 的无功输出降为零，GT3 和DE 的无功输出为负，DE 的有功输出消减了120 kW.这是因为在荷谷时段，母线节点电压较高，而有功消减成本比提供无功支持的成本高得多，因此，主要借助无功调节来调压:减少无功功率输出(例如GT1、GT2)或发出容性无功功率(例如GT3 和DE). 由表3 可看出，荷峰时段各GT 的功率因素调整为0.8，增加了无功输出，从而提升母线节点电压.

日内调度调整前后的DG 母线和主要负荷母线A 相的相电压幅值曲线如图5、图6 所示.

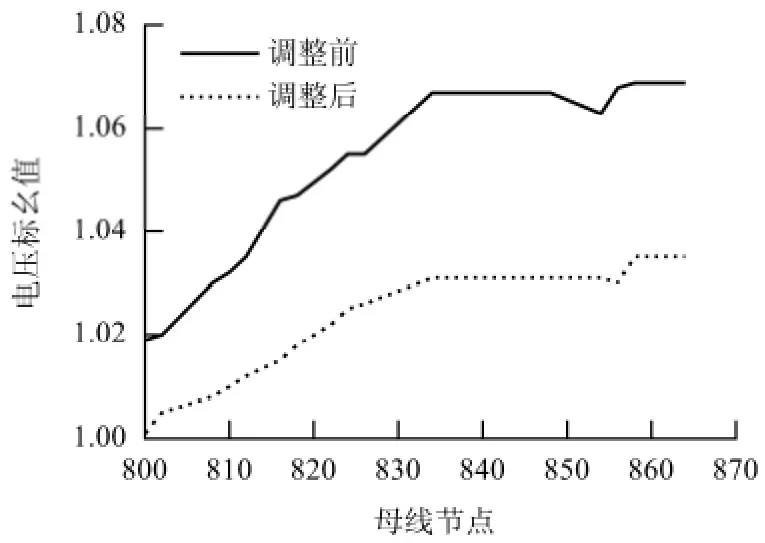
图5 荷谷时段各母线A 相电压曲线Fig.5 Phase-A voltage profiles at various network buses in load trough period

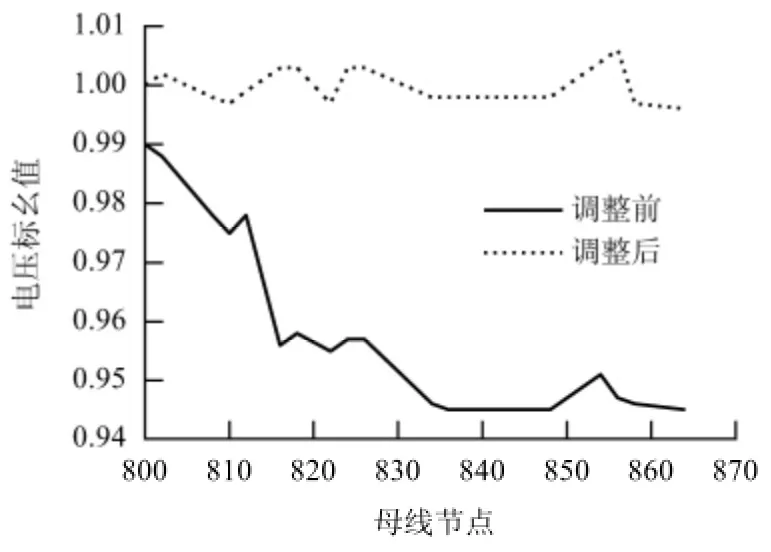
图6 荷峰时段各母线A 相电压曲线Fig.6 Phase-A voltage profiles at various network buses in load peak period

由图5 ～6 可看出，通过日内优化调整日前调度值后，无论是荷谷时期还是荷峰时段，母线节点电压都由原来的越限状态恢复到电压规定范围内(±5%以内)，这样可避免引起电压越限的DG 被过压(或低压)保护装置切除.

4 结束语

本文针对主动配电网的技术特点及其现有优化调度方法存在的问题，提出了两阶段一体化调度方法:日前经济优化调度和日内滚动修正. 日前优化调度模型以分布式能源、储能单元及可控负荷为调度对象，以整个调度周期内主动配电网的运行成本最小为目标，使配电网的长期运行更经济.

为了避免高渗透率的DG 引起过压等问题而被切除，在日内实时优化调度模型中，将可调DG的无功功率也作为优化变量，参与配电网的电压调整，实现可调DG 的有功功率输出和无功功率输出的全局最优分配，提高配电网消纳新能源的能力.最后通过算例结果分析，验证了所提主动配电网优化调度模型的正确性和有效性.

本文所研究的主动配电网优化调度模型是建立在市场电价和可控负荷补偿价格为已知的基础上的，有待进一步将市场电价和需求响应策略融入到优化调度模型中，使主动配电网获得更好的优化经济运行效果.

致谢:本文工作得到成都信息工程大学引进人才项目(KYTZ201317)的资助.

［1］ 王成山，李鹏. 分布式发电、微网与智能配电网的发展与挑战［J］. 电力系统自动化，2011，34(2):10-14.WANG Chengshan， LI Peng. Development and challenges of distributed generation，micro-grid and smart distribution network［J］. Automation of Electric Power Systems，2011，34(2):10-14.

［2］ 范明天，张祖平，苏傲雪，等. 主动配电系统可行技术的研究［J］. 中国电机工程学报，2013，33(22):12-18.FAN Mingtian，ZHANG Zuping，SU Aoxue，et al.Enablingtechnologiesforactivedistribution systems［J］. Proceedings of the CSEE，2013，33(22):12-18.

［3］ 陈道君，龚庆武，张茂林，等. 考虑能源环境效益的含风电场多目标优化调度［J］. 中国电机工程学报，2011，31(13):10-17.CHEN Daojun，GONG Qingwu，ZHANG Maolin，et al.Multi-objective optimal dispatch in wind power integrated system incorporating energy-environmental efficiency［J］. Proceedings of CSEE，2011，31(13):10-17.

［4］ 洪博文，郭力，王成山. 微电网多目标动态优化调度模型与方法［J］. 电力自动化设备，2013，33(3):100-107.HONG Bowen，GUO Li，WANG Chengshan，et al.Model and method of dynamic multi-objective optimal dispatch for microgrid［J］. Electric Power Automation Equipment，2013，33(3):100-107.

［5］ WIERZBOWSKI M， OLEK B. Integration of the embedded generation into distribution systems at the competitive markets［C］∥Innovative Smart Grid Technologies Conference (ISGT 2014). Washington D.C.:IEEE，2014:1-5.

［6］ 尤毅，刘东，钟清，等. 主动配电网优化调度策略研究［J］. 电力系统自动化，2014，38(9):177-183.YOU Yi，LIU Dong，WU Qing，et al. Research on optimal schedule strategy for active distribution network［J］. Automation of Electric Power Systems，2014，38(9):177-183.

［7］ 窦震海，牛焕娜，高燕，等. 主动型配电网日前调度策略研究［J］. 农业工程学报，2014，30(11):126-133.DOU Zhenhai，NIU Huanna，GAO Yan，et al. Study on day-ahead dispatch strategy of active distribution network［J］. Transactions of the Chinese Society of Agricultural Engineering，2014，30(11):126-133.

［8］ GILL S，KOCKAR I，AULT G W. Dynamic optimal power flow for active distribution networks［J］. IEEE Transactions on Power Systems，2014，29(1):121-131.

［9］ AYMAN B，SALAMA M M A. Management scheme for increasing the connectivity of small-scale renewable DG［J］. IEEE Transactions on Sustainable Energy，2014，27(1):1-8.

［10］ BARTONA J，HUANGB S，DAVID I. The evolution of electricity demand and the role for demand side participation in ADN［J］. Energy Policy，2013，52(5):85-102.

［11］ 刘小聪，王蓓蓓，李扬. 智能电网下计及用户侧互动的发电日前调度计划模型［J］. 中国电机工程学报，2013，33(1):30-38.LIU Xiaocong，WANG Beibei，LI Yang. Day-ahead generation scheduling model considering demand side interaction under smart grid paradigm［J］. Proceedings of the CSEE，2013，33(1):30-38.

［12］ 刘自发，刘刚，刘幸. 基于量子差分进化算法的分布式电源协调优化调度［J］. 电网技术，2013，37(7):1922-1928.LIU Zifa，LIU Gang，LIU Xing. Coordinated optimal dispatching of distributed generation based on quantum differential evolution algorithm［J］. Power System Technology，2013，37(7):1922-1928.

［13］ 王彩霞，鲁宗相. 风电功率预测信息在日前机组组合中的应用［J］.电力系统自动化，2011，35(7):13-18.WANG Caixia，LU Zongxiang. Unit commitment based on wind power forecast［J］. Automation of Electric Power Systems，2011，35(7):13-18.

［14］ 刘杨华，吴政球，涂有庆，等. 分布式发电及其并网技术综述［J］. 电网技术，2008，32(15):71-76.LIU Yanghua，WU Zhengqiu，TU Youqing，et al. A Survey on distributed generation and its networking technology［J］. Power System Technology， 2008，32(15):71-76.

［15］ 耿立卓. 智能配电网状态估计与测量配置［D］. 天津:天津大学，2011.