基于Petri 网的拖车到达调度优化模型与仿真

蔡文学， 钟冠恒， 胡清浩， 钟慧玲

(华南理工大学经济与贸易学院，广东 广州510006)

珠三角内河集装箱码头进口集装箱必须经过海关全部查验后才能集中放行，由于堆场容量限制，集中到达的大量进港拖车只能在闸口外等待，导致城市交通要道阻塞. 以佛山三水港为例，进港拖车从下午5 点开始大量到达，1 h 后等待进港拖车的数量最多达60 辆，直到下午8 点才开始缓解.此问题在珠三角内河码头普遍存在.原因是珠三角城镇一体化显著，内河码头一般位于城镇区域甚至接近城镇中心的位置，大量等待进港的拖车阻碍了城市交通，由此产生的城市交通管制又影响了拖车运输，进一步降低了物流效率.

解决港口等待拖车过多的方法，一是港口闸口设计优化，确定最优闸口通道量，文献［1］使用排队系统建立港口大门的作业模型，并仿真得到满足通行量的港口最小通道数量;文献［2］通过仿真测试港口闸口有效通行量确定闸口性能，分析港口最佳闸口数量，增加闸口单位时间内的通过量，从而减少等待进港拖车的数量. 二是港内堆场调度优化，通过提升港口堆场作业效率，缩短拖车在港内停留时间.文献［3］通过优化拖车在港作业路径，提高了堆场作业效率;文献［4］提出港口内拖车调度的混合策略，通过离散事件仿真对混合策略的评价函数进行了优化，加快了港口内部运作速度. 三是拖车到达调度优化，缓解到达高峰. 文献［5］用BCMP(Baskett Chandy Muntz Palacios)排队网络优化集卡到达调度，并用算例验证了有效性;文献［6］分析了拖车到达信息对港口利润的影响，仿真证明拖车有序到达能减少港口运作成本.

珠三角内河集装箱码头多属于中小型码头，由于地理位置限制，码头面积有限. 随着区域经济的高速发展，多数港口的年吞吐量早已超过10 万标准箱，港口堆场容量与闸口通道基本处于满负荷状态.因此，通过优化闸口设计和堆场作业调度难以解决等待拖车过多的问题.本文对进港拖车到达调度模式进行优化，将拖车随机集中到达变为分批定量有序到达，缓解高峰时段拖车到达过多的问题，是解决目前珠三角内河集装箱码头进港拖车交通拥堵和物流效率低下的可行方法.

基于拖车到达作业过程的离散随机性与并发性的特点，建立了拖车到达作业过程的混合Petri网模型，对模型中库所令牌的数量与时间戳属性进行统计，分析进港拖车的到达数量、等待时间、最大队长等参数，然后，利用Arena 仿真确定拖车调度方案，量化拖车调度优化效果.

1 拖车到达作业过程的Petri 网模型

1.1 拖车到达作业过程

拖车到达作业过程属于线性流程. 具体流程如下:

(1)拖车到达:在港口闸口外等待堆场资源.

(2)入闸流程:堆场容量允许其进入后，拖车经过港口闸口进入堆场，拖车进入港口闸口、海关闸口交单验单过程.

(3)堆场作业:拖车进入指定堆场，按业务类型完成提卸箱作业，完成作业后离开.

(4)出闸流程:拖车驶出港口闸口、海关闸口交单验单过程.

(5)拖车离开:拖车完成作业后，经过海关闸口与港口闸口离开港口.

闸口通行取决于两个条件:

(1)工作时间，以海关闸口工作时间为准.

(2)堆场能力，为避免堆场内拖车堵塞，影响作业效率，只有在堆场能力满足时才能进港.

拖车到达港口属于离散随机事件，通过到达速率或到达间隔分布可以模拟港口拖车的到达规律.根据珠三角内河码头集中放行的特点，拖车到达速率随时间改变，用变化的到达速率比单一间隔时间分布能更好地体现拖车到达规律，而非平稳泊松过程对车辆到达之类的多发独立随机事件有较好的模拟效果［7-8］.因此，采用用非平稳泊松过程模拟拖车的到达规律.

非平稳泊松过程中一次只有一个事件发生，且事件的发生互相独立，在时间间隔［τB，τE］内事件发生量服从速率函数λ(τ)的泊松分布，因此，时段内事件发生期望数是与时间间隔τB-τE和速率函数λ(τ)有关的泊松随机变量.

从时刻τB到时刻τE，业务类型x 拖车的到达期望值为

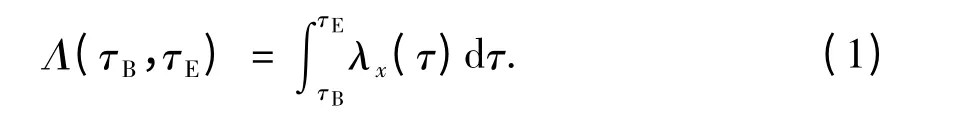
λ(τ)为某时段内某种业务类型拖车的到达速率函数，与业务类型x 及时间τ 有关，λx(τ)越大，在时间间隔［τB，τE］内事件发生次数越多.上述随机变量可以在Petri 网中利用变迁的随机发生来模拟拖车的随机到达.

1.2 混合Petri 网模型

Petri 网具有简单、描述并发事件能力强、过程直观等特点，常用于描述异步的、并发的系统模型，并发展出多种高级Petri 网模型. 利用Petri 网描述配合仿真验证的方法，在不同领域特别是港口物流研究中得到了广泛应用［9-12］.

根据珠三角内河港口进港拖车的作业特点，本文通过对受控Petri 网、有色Petri 网、时延Petri 网以及随机Petri 网的分析［13-15］.

令牌token 是Petri 网中流动的实体，表示实际作业的拖车.采用混合Petri 网模型

Σ= (P，T，F，M，C，B，K，I，H)

进行建模，其中:

(P，T，F)是基本Petri 网，P 为有限库所集，T 为有限变迁集，F 为库所集到变迁集的有向流集合.

Pq∈P 为队列库所集，表示拖车队列的库所.

Pd∈P 为时延库所集，表示令牌在库所中随机逗留一段时间后才能离开.

Pc∈P 为选择库所集，表示令牌在库所中按规则集R 选择即将发生的变迁，用于表达拖车在作业过程中对不同路径或闸口的选择.

Ta∈T 为随机变迁集，变迁随机发生的期望值Λ(tB，tE)(式(1))与速率函数λ(t)有关. 用于表示各业务拖车的随机到达.

Tr∈T 为时延变迁集，用□表示，即变迁需要通过一个随机时延才能完成，每个时延变迁可看成两个瞬时变迁与一个时延库所的集合.

Tc∈T 为受控变迁集.

Tu∈T 为非受控变迁集，表示闸口或堆场作业的随机时延.

M 为网的标识集;

C 为控制库所集，

C∩P=∅;

B 为从控制库所影响可控变迁的有向弧集，它的元素称为控制弧，表示受堆场容量限制的拖车放行条件，

B⊆C×Tc;

K 为令牌颜色集，用于标记拖车业务类型与到达时间、离开时间等时间戳，

K={k1，k2，…};

H 为全局时钟，作为时间戳的记录标准;

I 为抑止弧集，

I⊂P×T， I∩F=∅.

若

(1)∀p∈P∶(p，t)∈F→M(p)≥1，

(2)∀p∈P∶(p，t)∈I→M(p)=0.

对t 有M［t ＞.即当抑止弧前端库所存在令牌时，阻止抑止弧末端的变迁执行，用以表达拖车进入的优先级.

1.3 变迁使能条件

∀p∈·t，若(p，t)∈F，且M(p)≥W(p，t)，则对t∈T，t 具有发生权，称t 标识M 下使能.而对混合网Σ，当且仅当M(p)≥W(p，t)且控制u 使能时，变迁t∈Tc才能发生.对于控制u 的使能状态，由某库所令牌总数ΣM(pi)与当前时刻τ 共同决定，设z 为令牌总数的上限，τbeg、τend分别为仿真时钟的时间上限与时间下限，当

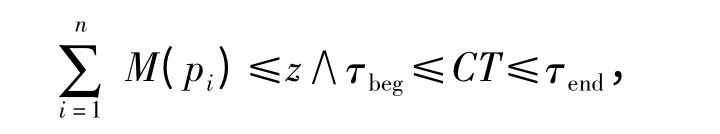
控制u 使能.例如，当

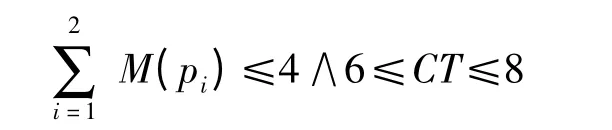
时，库所p1与p2的令牌总数≤4，且仿真时钟在6 点到8 点之间，变迁t 有发生权.

1.4 基本性质检验

有界性:设港口每天作业拖车总量为O，一天中任一时刻系统中的拖车数m，必有m≤O. 通过观察Σ 知，任取可达标识Mi都必有

Mi(p)≤m≤O，因此，Σ 为结构有界.

活性:对Σ 的运行进行分析可以看出，每个变迁在特定的变迁序列下都能重获发生权，因此，Σ 为活网.

死锁:为了保证不出现库所永远无令牌的情况，必须检验网Σ，证明其中不包含死锁.根据Petri网死锁的定义，对于库所P，不存在任何库所子集满足·pi⊆p·

i ，因此，Σ 不存在死锁.

1.5 模型假设

通过对港口作业的实际调研发现:

(1)进港拖车一般只执行单一业务，极少出现拖车空箱进港，重箱离港等混合业务.

(2)港口在海关集中放行后，大量拖车到港进行提取重箱业务造成拖车阻塞问题.

(3)由于海关查验需要货箱单层平铺，查验堆场一般处于饱和状态，因此，每天放行集装箱量基本稳定.

(4)提取重箱业务不受其他业务活动干扰.根据上述实际作业特点，对拖车到达作业模型做以下假设:

(1)拖车业务单一性.

进港拖车只进行提取重箱或提取空箱等一种业务，且重点分析提取重箱拖车.

(2)堆场作业时间相对稳定.

由于查验堆场处于饱和状态，作业时间不受外部因素影响，可认为每辆拖车的堆场作业时间相对固定，符合一定的时间分布.

1.6 模型分析

网Σ 的运作如下，不同颜色令牌代表不同业务拖车随机到达队列库所集合排队，当控制u 使能即入闸条件允许，拖车通过闸口后，进入选择库所并根据规则发生不同时延变迁，拖车完成作业后离开网Σ.

用等待拖车最大数量与拖车等待时间评价拖车到达调度的效果.等待拖车最大数量是衡量拖车阻塞程度的指标，等待时间反映出拥堵的严重程度.通过对队列库所集合Pq中的令牌数进行统计，就可以得到一段时间内Pq中令牌的最大数量. 对进入与离开Pq的令牌建立时间戳，通过统计可得到一段时间内令牌在Pq中的逗留时间.

在时间［τB，τE］内，有输入集:

通过输入集X，在到达率λx(τ)下，统计时间［τB，τE］内M(Pq)与令牌的时间戳可以得到输出集:

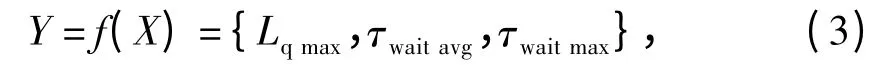
式中:f(X)为传递函数，通过Petri 网构建，利用Arena 仿真软件实现，由到达批量与间隔时间的输入集X，得到输出集Y;

Lqmax为拖车等待队列的最大长度;

τwaitavg为拖车平均等待时间;

τwaitmax为拖车最大等待时间.

通过输出集可得拖车的最大等待时间、平均等待时间与等待队长，根据这3 个指标分析港口拖车当前的阻塞程度，并衡量拖车调度优化后的效果.

2 拖车到达作业过程的Petri 网模型

2.1 三水港拖车到达作业过程简介

佛山市三水港位于珠江三角洲的西北端北江与西江的汇流处，工作时间为每周6 d 早午晚3 时段制，其拖车业务主要包括提取和卸载重箱及提取和卸载空箱4 种，港内有2 个主要堆场，到达作业流程与1.1 节中的拖车到达作业过程相同.

2.2 拖车到达作业过程模型

建立拖车作业流程的混合Petri 网模型Σ，如图1 所示.

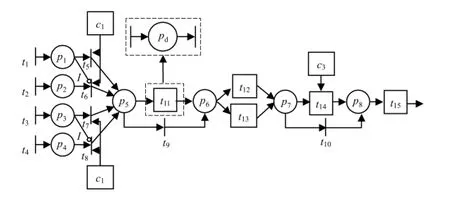
图1 三水港拖车到达作业过程Petri 网模型Fig.1 Trailer arrival and operation process Petri net model of Sanshui Port

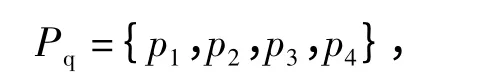
式中:p1～p4分别表示卸载空箱、提取空箱、卸载重箱、提取重箱4 种业务拖车的等待队列库所.

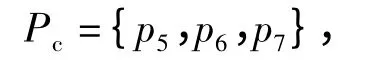
式中:p5、p6、p7分别表示入闸海关是否查验、进入重/空箱堆场、出闸海关是否查验的3 个选择库所.

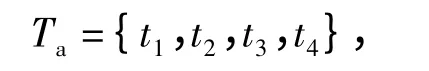
式中:t1～t4分别表示4 种业务拖车的随机到达.

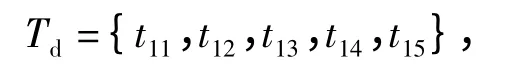
式中:t11～t15分别表示实际的作业环节，例如:海关入闸验单、堆场装卸箱、海关出闸检查、港口出闸验单.

以t11为例，一个时延变迁可以分解为两个瞬时变迁与一个时延库所的集合.

2.3 仿真建模

建立拖车到达作业过程的Petri 网模型后，将网Σ 中各个部分转换为Arena 仿真系统中的相应模块，即可得到拖车到达作业的仿真模型，其中:

使用Create 模块替代随机发生变迁集Ta的活动，实现作业拖车的随机到达;

使用Assign 模块中的Attribute 记录颜色集K与时间戳，用于记录拖车的不同业务与进出时刻;

使用Queue 模块替代队列库所集合Pq的活动，并利用Queue 模块中的Priority 属性来体现抑止弧集I，抑止弧前端的队列库所优先级高;

使用Decide 模块与Route 模块替代选择库所集Pc的活动，实现实体的选择活动;

使用Seize、Resource、Release 模块替代控制库所集C 的活动;

使用Process、Delayv 等模块替代时延变迁集Tr的活动.

通过转换后得到的Arena 仿真模型如图2 所示，包括拖车到达、进入闸口、堆场作业、离开闸口4 个部分.

2.4 模型验证

图3 为三水港拖车离港记录.

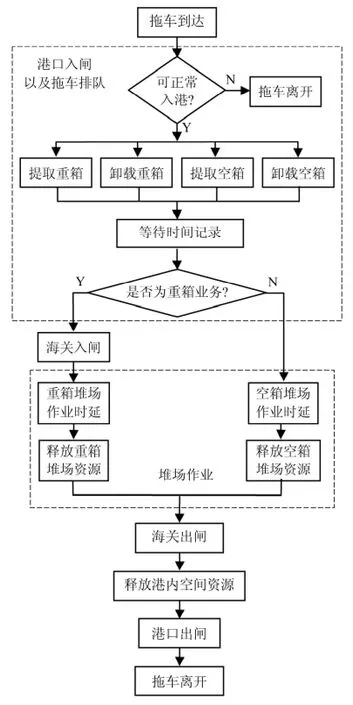
图2 三水港拖车到达作业过程的Arena 仿真模型结构Fig.2 Arena simulation model structure based on trailer arrival and operation process of Sanshui Port

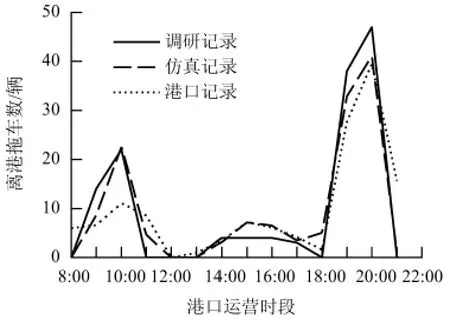
图3 三水港拖车离港记录对比Fig.3 Comparison of trailers departure records of Sanshui Port

为验证模型的有效性，将仿真港口拖车离港分布与调研报告、港口提供的拖车离港分布进行对比.拖车离港的数量与时间由拖车到港数量、到港时间、等待时间、堆场处理能力、堆场处理时间、闸口处理时间等因素共同决定，能充分反映港口拖车的到达作业过程规律.

图3 显示仿真结果与调研记录、港口记录的拖车离港规律特别是高峰时段的到达规律高度吻合，且仿真得到的平均等待时间与最大队长与调研报告中观察到的基本相符，表明模型能够反映港口拖车的到达作业过程.

3 拖车调度方案优化

进港拖车阻塞问题表现为进港拖车等待时间过长和等待队长过长. 优化目标为:通过改变到达间隔τa与到达批量b 使等待时间与队长最短，即令

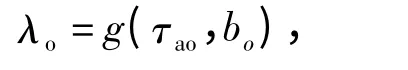
代入X(λo，τB，τE)中，使下式成立，

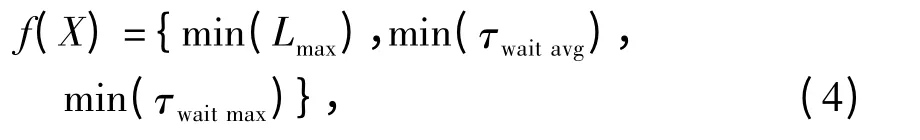
式中:τao为最佳时间间隔;

bo为最佳批量;

λo为τao与bo下最佳到达率.

三水港重箱堆场作业平均费时

τavg=38 min.

理论上，当

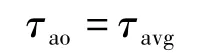
时，拖车等待时间最短. 为便于港口计划，简化问题，设定到达间隔时间为30 min.令

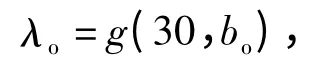
代入X(λo，τB，τE)中，使式(4)成立.

检验以下两个基本到达调度方案.

(1)方案1

不改变各工作时段提箱拖车到达的数量，但改变时段内到达的批量，令拖车到达数量适应时段内的堆场作业能力.

(2)方案2

在方案1 的基础上，改变各时段拖车到达量的比例，使拖车到达量适应该时段港口堆场作业能力.拖车的到达调度，主要改变了拖车的到达规律，实现批量到达，建模重点在于确定不同时段内时间间隔τa与拖车到达批量b.

假设所有车辆都能准时到达，且所有车辆到达时间误差服从三角分布，即Tri(-5 min，0 min，5 min)，提早或延迟时间均不超过5 min.以到达高峰的晚上时段为例，设

τa= 30 min， b ∈［15 辆，25 辆］，

利用PAN(process analyzer)的分析结果见表1.

晚上时段作业时间均值为195 min，最大等待时间超过195 min 则表示超出作业时间而在堆场内过夜的车辆.当间隔时间为30 min，批量为21 辆时，等待时间、最长等待队长、超时车辆都相对较少，因此，选择为晚上时段分析到达规律，用同样的方法可得到所有时段的到达批量，如表2 所示.

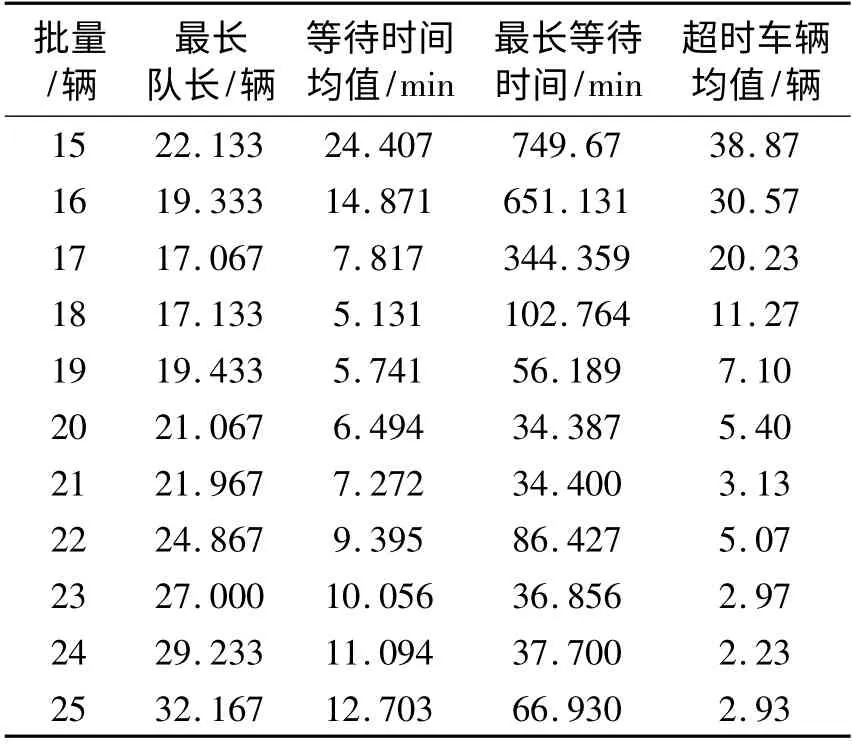
表1 方案1 的PAN 仿真报告Tab.1 PAN simulation report of solution 1

表2 方案1 到达调度批量Tab.2 Scheduled arrival quantity of solution 1

4 仿真结果分析

改进前与两种方案的30 次仿真结果见表3 和表4(仿真时间长度为6 d).

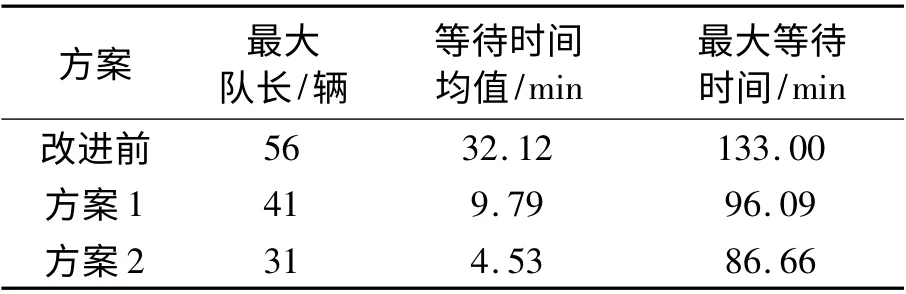
表3 最大队长、平均等待时间与最长等待时间的比较Tab.3 Comparison of the maximum queue length，the average waiting time，and the maximum waiting time

(1)方案1 对工作时段内拖车到达进行调度，平均等待时间从原来的32 min 减少至9 min，最大等待时间从133 min 减少至96 min.最大的等待车辆数从原来的56 辆减少至41 辆.由表4 的等待时间分布比较可知，到达调度后拖车等待时间80%以上集中在30 min 内，表明到达调度能减少大部分拖车的等待时间.

(2)方案2 对全天内的拖车进行到达调度，可进一步减少平均等待时间与等待车辆数，并有效增加堆场利用率，减少过夜车辆.

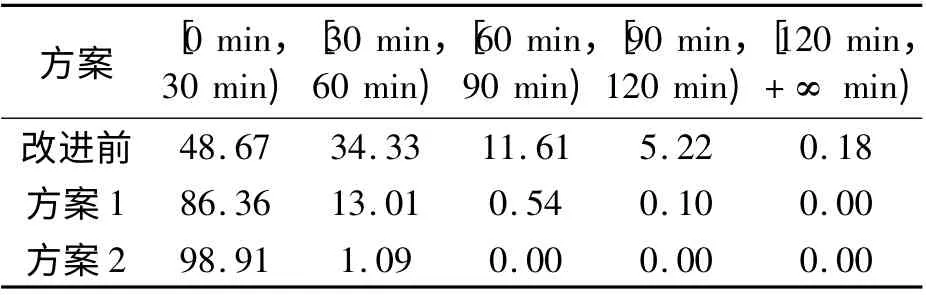
表4 等待时间分布比较Tab.4 Comparison of waiting time distribution

图4 为30 次仿真拖车等待时间均值的比较.

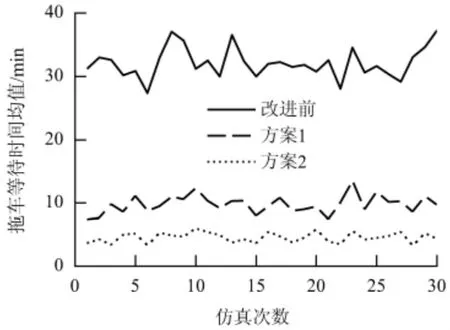
图4 30 次重复仿真拖车等待均值比较Fig.4 Comparison of average waiting time based on 30 replications

由表3 和表4 可见:

(1)方案1 对工作时段内拖车到达进行调度，平均等待时间从原来的32 min 减少至9 min，最大等待时间从133 min 减少至96 min.最大的等待车辆数从原来的56 辆减少至41 辆.由表4 的等待时间分布比较可知，到达调度后拖车等待时间80%以上集中在30 min 内，表明到达调度能减少大部分拖车的等待时间.

(2)方案2 对全天内的拖车进行到达调度，可进一步减少平均等待时间与等待车辆数，并有效增加堆场利用率，减少过夜车辆.

5 结束语

针对珠三角内河集装箱码头的进港拖车阻塞交通的问题，提出拖车到达过程的混合Petri 网模型，对佛山三水港进行建模，通过Arena 仿真确定拖车到达调度的间隔时间与到达批量，并验证调度方案的优化效果. 仿真结果显示，拖车等待时间最高减少87%，等待数量减少26%，证明拖车到达调度优化能有效降低闸口外进港拖车的等待时间与等待数量，对改善内河集装箱码头运行效率具有实际应用意义.

致谢:本文工作得到佛山市港口引用RFID 技术试点项目(FSHL2012192G)的资助.

［1］ 金淳，于越，赵璐. 基于仿真优化的集装箱港口大门作业调度研究［J］. 系统仿真学报，2008，20(8):1998-2001.JIN Chun，YU Yue，ZHAO Lu. Research on optimal scheduling on gate operation on container terminal based on simulation optimization method［J］. Journal of System Simulation，2008，20(8):1998-2001.

［2］ 金淳，沈剑峰. 基于仿真的港口大门服务系统性能测试［J］. 系统仿真学报，2008，20(9):2429-2432.JIN Chun， SHEN Jianfeng. Simulation-based performance test for service information system of gate operation on container port［J］. Journal of System Simulation，2008，20(9):2429-2432.

［3］ 王军，徐晓雷. 集装箱码头集卡作业的路径选择［J］.大连海事大学学报，2011，37(2):25-27.WANG Jun，XU Xiaolei. Route selection of container trucks in container terminal［J］. Journal of Dalian Maritime University，2011，37(2):25-27.

［4］ TAO Jinghui，CAI Han，ZHANG Xiaoping. A mixed scheduling method for vehicle dispatching in container terminals［J］. Operations Research Transactions，2009，13(3):10-22.

［5］ 曾庆成，张笑菊，陈文浩，等. 基于BCMP 排队网络的码头集卡预约优化模型［J］. 系统工程学报，2013，28(5):592-599.ZENG Qingcheng，ZHANG Xiaoju，CHEN Wenhao，et al. Optimization model for truck appointment based on BCMP queuing network［J］. Journal of Systems Engineering，2013，28(5):592-599.

［6］ ZHAO Wenjuan，GOODCHILD A V. The impact of truck arrival information on container terminal rehandling［J］. Transport Research Part E:Logistics and Transportation Review，2010，46(3):327-343.

［7］ ERHAN C. Introduction to stochastic processes［M］.［S. l.］:Prentice-Hall，Inc.，1975:94-101.

［8］ 许巧莉，孙丽君，胡祥培，等. 非平稳到达的码头集卡预约优化模型［J］. 大连理工大学学报，2014，54(5):589-596.XU Qiaoli， SUN Lijun， HU Xiangpei， et al.Optimization model for appointment of container trucks with non-stationary arrivals［J］. Journal of Dalian University of Technology，2014，54(5):589-596.

［9］ 李望，倪少权. 基于TPr/T-S 的客专车站通用模型及仿真［J］. 西南交通大学学报，2013，48(5):934-941.LI Wang，NI Shaoquan. General model and simulation research on passenger-dedicated line station based on TPr/T-S［J］. Journal of Southwest Jiaotong University，2013，48(5):934-941.

［10］ 张耀鸿，樊建才，廖晓林. 基于Petri 网的指挥控制流程仿真方法［J］. 系统仿真学报，2012，24(7):1418-1421.ZHANG Yaohong， FAN Jiancai， LIAO Xiaolin.Simulation method of command and control process based on Petri net［J］. Journal of System Simulation，2012，24(7):1418-1421.

［11］ 鲁工圆，闫海峰，徐进. 基于TCPN 的铁路客运站作业组合仿真模型［J］. 西南交通大学学报，2013，48(4):694-701.LU Gongyuan， YAN Haifeng， XU Jin. Railway passenger station operation combined simulation model based on TCPN［J］. Journal of Southwest Jiaotong University，2013，48(4):694-701.

［12］ 郑文艳. 分层有色Petri 网在物流配送系统仿真建模中的应用［J］. 计算机系统应用，2014，22(4):164-168.ZHEN Wenyan. Modeling and simulation in logistics systems based on hierarchy coloured petri net［J］.Computer Systems and Applications，2014，22(4):164-168.

［13］ 吴哲辉. Petri 网导论［M］. 北京:机械工业出版社，2006:251-263.

［14］ JENSEN K. Coloured Petri nets-basic concepts，analysis methods and practical use，Vol. 1［M］. 2nd ed. Heidelberg:Springer，1996:1-234.

［15］ RAMCHANDANI C. Analysis of asynchronous concurrent system by timed Petri nets［D］.Cambridge:MIT，1974.