广义Kelvin 蠕变损伤模型及其参数的智能辨识

徐国文， 何 川， 代 聪， 王士民

(西南交通大学交通隧道工程教育部重点实验室，四川 成都610031)

岩石的流变特性是岩石内在的时间特性，为了更准确地描述岩石的三阶段流变变形特性，许多学者考虑岩石流变过程中的损伤，建立流变本构模型时引入了损伤力学理论.

高赛红等在流变模型中考虑了硬化-损伤效应［1］;陈卫忠等考虑了黏滞系数损伤对岩石结构长期特性的影响［2］;朱昌新等研究了岩石蠕变的时效损伤［3］;K S Chan 等将损伤理论引入盐岩流变的研究中［4］;杨圣奇等将岩石蠕变损伤演化特性分为2 个阶段，考虑了损伤对岩石流变特性的影响［5］.

由于实际工程的需要，一些学者借助商业软件开发平台进行模型的二次开发.以FLAC3D 软件为例，杨文东等将Burgers 损伤模型用于边坡长期安全的研究［6］;黄明等对隧道围岩在含水条件下的劣化进行了分析［7］.

本文在五参数广义Kelvin 模型的基础上，基于Lemaitre 应变等效原理，提出了考虑岩石蠕变过程中材料劣化效应的广义Kelvin 蠕变损伤模型，并对该模型进行了二次开发;结合FLAC3D 数值计算程序及Matlab 平台，采用粒子群算法、模拟退火算法与FLAC3D 相结合的方法对已有试验数据进行反演.

1 广义Kelvin 蠕变损伤模型

广义Kelvin 模型(图1(a))由1 个弹性体和2 个Kelvin 体构成，不能反映岩石的塑性特性和加速蠕变过程.因此，将流变参数的损伤特性和M-C(摩尔-库伦)元件［8］引入该模型，建立广义Kelvin蠕变损伤模型(图1(b)).

图1 2 种流变本构模型Fig.1 Rheological constitutive models

(1)σ≤σf时

本构方程为:

式中:ε 为总应变;σ 和σf分别为总应力和屈服应力;Ei和ηi(i =1，2)分别为2 个Kelvin 损伤体的弹性模量和黏滞系数;Eh为弹性损伤体的弹性模量;Dt=1 - e-at为损伤变量［6］，其中a 为损伤参数，t 为时间.

由式(1)得到一维蠕变方程:

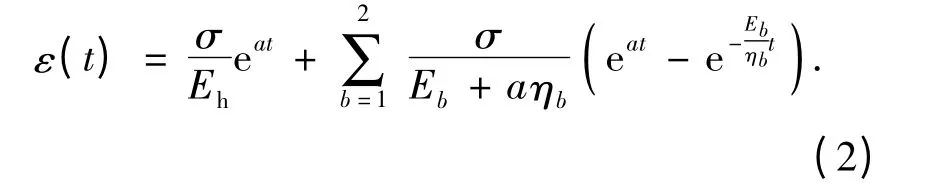
三维轴向蠕变方程为:

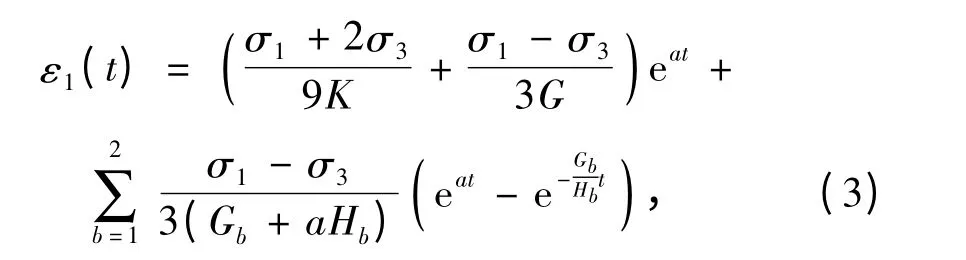
式中:ε1为轴向蠕变;K 为体积模量;G 为剪切模量;σ1和σ3分别为最大与最小主应力;Gb和Hb(b=1，2)分别为2 个Kelvin 损伤体的三维剪切模量和三维黏滞系数.

(2)σ ＞σf时

模型总应变为:

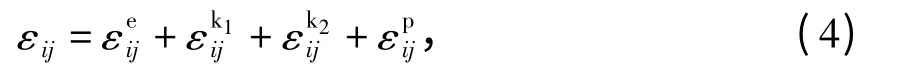
式中:εij为总应变;为弹性损伤体的应变;和分别为2 个Kelvin 损伤体的应变;为塑性体的应变.

偏量行为由式(5)描述:

式中:Sij为偏应力.

式中:δij为克罗内克函数(当i =j 时，δij=1;当i≠j时，δij=0);λ 为塑性指示因子;为塑性体应变.

式中，g 为与屈服准则对应的势函数.

塑性体采用带拉伸截止限的摩尔-库伦屈服准则，屈服函数

采用非关联流动准则，有势函数

体应力速率

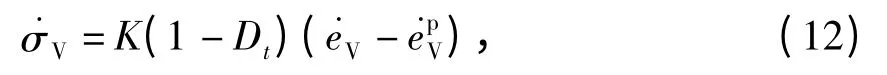
式中:σV为体应力;eV为总的体应变.

模型三维本构方程的差分形式为:

式中:Δt 为时间步;Ab=1 +GbΔt/(2Hb);Bb=1 -GbΔt/(2Hb);和分别为Δt 内新、旧应力偏量;和分别为Kelvin 体的新、旧应变偏量.

式中:

Δeij为Δt 内的总应变增量为Δt 内的塑性应变增量.

体应力的差分表达式为:

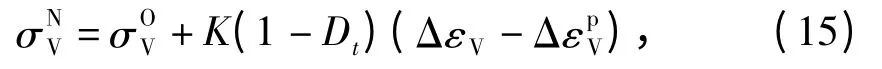
同理，Kelvin 体新的体应变

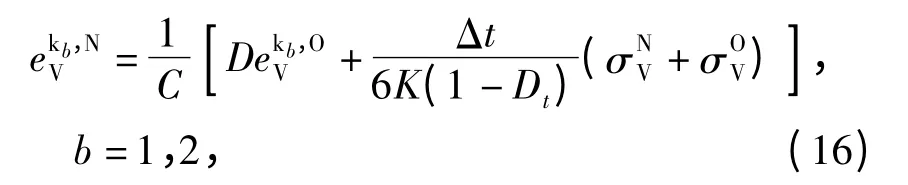
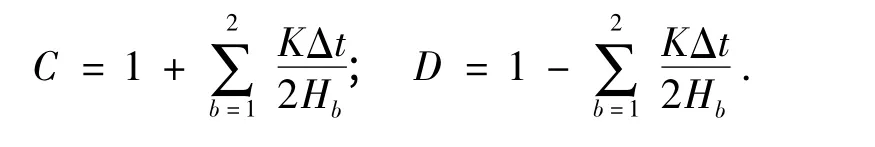
2 模型的程序实现与验证

基于FLAC3D，用C + +语言对模型进行了二次开发.广义Kelvin 蠕变损伤模型考虑了岩石的塑性和损伤特性，现用算例验证模型的正确性.

(1)塑性力学特性

对模型的塑性特性进行分析. 在广义Kelvin蠕变损伤模型(图1(b))的基础上去掉1 个Kelvin损伤体，且不考虑模型其余元件力学参数的损伤，此时广义Kelvin 蠕变损伤模型退化为考虑塑性的Kelvin 模型(图2). 模型参数:K =30 GPa，Gh=40 GPa(Gh为三维剪切模量)，G1= 60 GPa，H1=80 GPa·d，c = 12 MPa，φ= 30°，ψ = 10°，σte=1 MPa.计算模型取边长为1 m 的正方体，顶面施加20 MPa 均布荷载，其余各边施加相应的位移约束.图3 为蠕变30 d 后的塑性区.可见，2 种模型的塑性区范围一致，且主要集中在隧道洞周.

图2 考虑塑性的Kelvin 模型Fig.2 Kelvin model considering plasticity

图3 塑性区分布Fig.3 Distribution of plastic zone

(2)损伤力学特性

采用图4 所示模型进行损伤特性验证.该模型尺寸(水平×竖向)为5 cm×10 cm，底部固定竖直方向位移，顶部施加30 MPa 均布压力，记录点A 的竖向位移.

三参数广义Kelvin 模型(图2)的黏弹性参数和广义Kelvin 蠕变损伤模型的黏弹塑性参数取值同上. 新增元件参数取值:a = 0. 05 d-1，G2=60 GPa，H2=80 GPa·d. 图5 给出了2 种模型点A竖向位移随时间的变化曲线.

图4 数值模型Fig.4 A numerical model

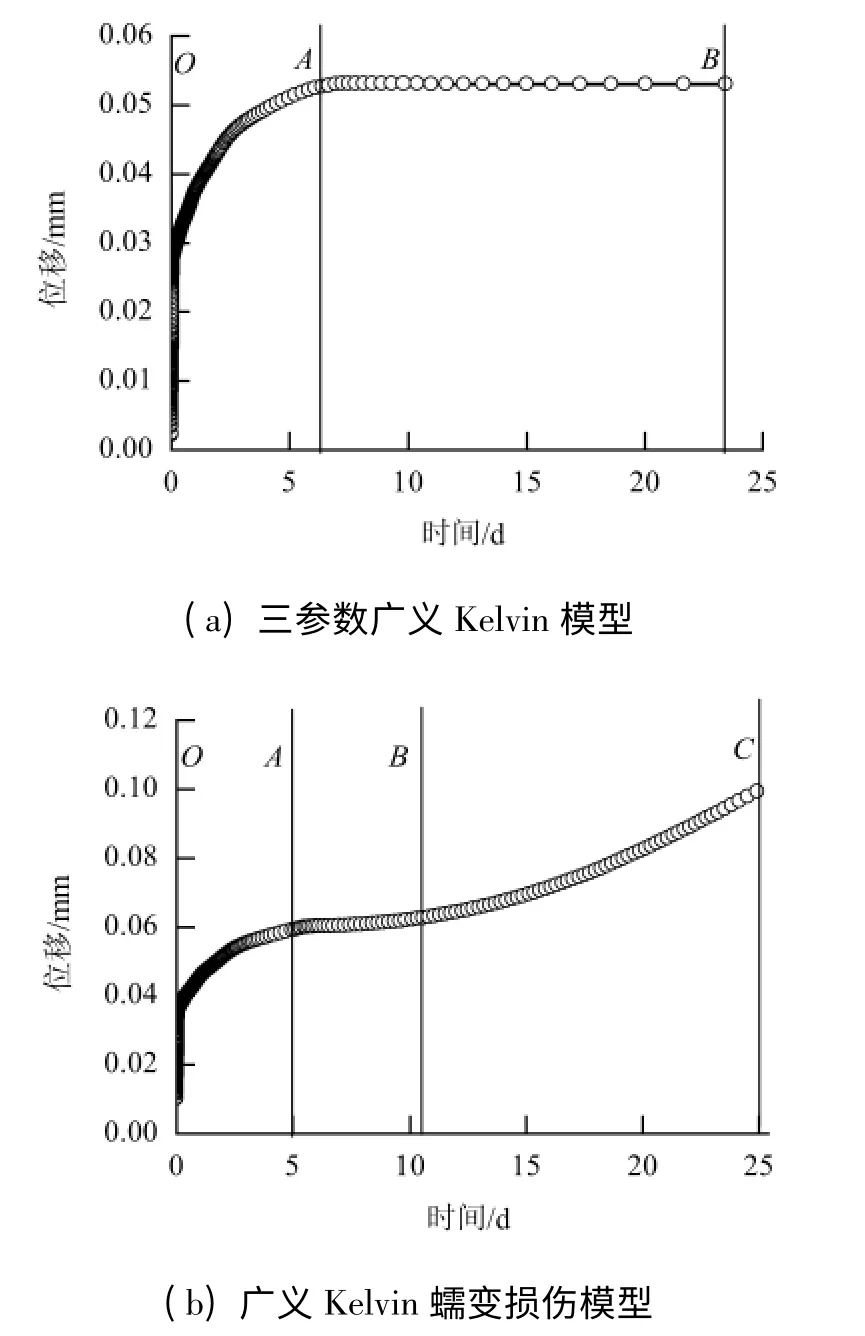
图5 点A 的竖向位移Fig.5 Vertical displacement of point A

可见，三参数广义Kelvin模型仅能反映衰减蠕变阶段(图5(a)中OA)及稳态蠕变阶段(图5(a)中AB);而广义Kelvin 蠕变损伤模型由于考虑了塑性与损伤，可反映岩石的非线性蠕变阶段(图5(b)中AB)和加速蠕变阶段(图5(b)中BC)，更符合岩石的特性.

3 模型参数智能辨识

3.1 参数辨识方法

将模拟退火算法［10］引入粒子群优化算法［11］，称为PSO(particle swarm optimization )-SA(simulated annealing)算法.具体步骤:

步骤1 建立目标函数

(1)获得试验数据{(t1，ε1)，(t2，ε2)，…，(tn，εn)}，确定设计变量R=(K，Gh，G1，G2，H1，H2，a);

(2)用FLAC3D 软件建立数值模型，采用广义Kelvin 蠕变损伤模型，将设计变量值代入计算，得到与(1)中试验数据对应的计算数据{(t1，～ε1)，(t2，)，…，(tn，)};

(3)建立目标函数F(R)，

步骤2 参数辨识

(1)在Matlab 环境下，采用PSO-SA 优化算法对参数进行初始化. 调用FLAC3D，将初始参数作为模型输入，求对应的变形量，通过式(17)求得每个粒子的适应值，然后返回Matlab 程序，取优更新个体与群体极值.

(2)计算粒子更新前、后的适应值，更新前后适应值之差为适应值变化量J. 若J ＜0，则粒子位置得到更新;若exp(-J/θ)＜γ(其中θ 为温度，γ 为取值［0，1］的随机数)，粒子位置同样得到更新，否则不更新.若接受新值，降温θ 变成kθ(k 为退火参数，k∈(0，1))，否则不降温，并返回步骤2，直至满足精度要求.

3.2 参数辨识结果

用粉砂岩轴向蠕变数据［12］和砂板岩蠕变数据［13］进行参数辨识.

M-C 体的材料参数由常规试验确定，具体可参考文献［12，14］.以K、Gh、G1、G2、H1、H2和a 为待求参量. 粒子群搜索空间:K = Gh= G1= G2∈(0，500 GPa)，H1=H2∈(0，500 GPa·d )，a∈(0，1);群体规模为100，最大搜索次数为100.模拟退火算法参数:初始温度θmax=5 000 ℃，温度最低取值θmin=0.01 ℃，温度退火参数k =0.9. 反演得到的参数见表1.

图6 为粉砂岩、砂板岩反演曲线与室内试验结果的比较，图7 为误差函数曲线.从图6 可见，反演曲线与试验结果吻合，说明模型能正确反映该岩石的各蠕变阶段. 从图7 可见，对于粉砂岩，PSO-SA优化算法在18 个迭代步内即达到了较高的收敛精度;对于砂板岩，由于其流变曲线较复杂，PSO-SA优化算法在40 步左右才达到全局最优. 误差曲线具有平台段，原因在于，为了解决PSO 算法易进入局部最优的缺陷，PSO-SA 优化算法有一定接受适应值较大粒子个体的概率，从而使得其本身也有可能进入局部最优［15］.但从结果看，只要达到一定迭代步，算法可以获得较好结果.

表1 流变参数反演结果Tab.1 Inversion results of rheological parameters

图6 反演结果与试验结果比较Fig.6 Comparison of inversion and test results

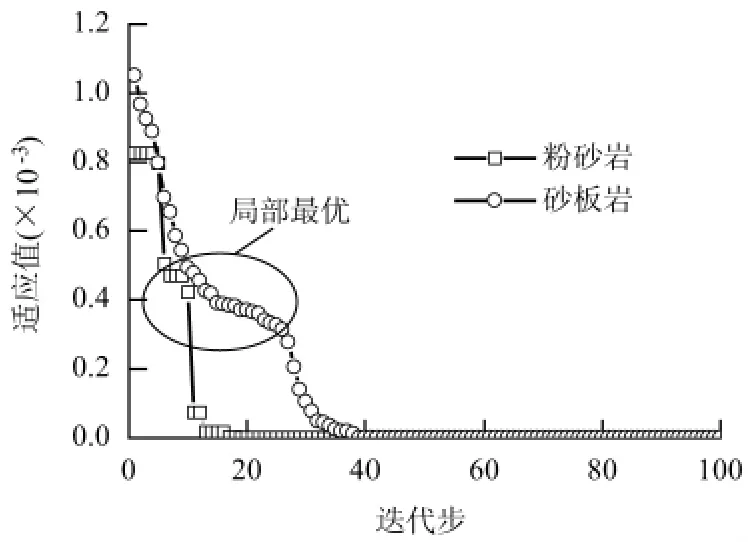
图7 误差曲线Fig.7 Error curves

反演算法的参数选择参考了已有研究成果，是基于经验进行的选择，因此产生了一定误差. 在智能算法中，如何优化算法自身参数以及算法理论的完善，还需要进行深入研究.

4 结 论

本文在五参数广义Kelvin 模型基础上，基于Lemaitre 应变等效原理，提出了广义Kelvin 蠕变损伤模型，并基于FLAC3D 软件提供的接口对模型进行了二次开发，获得以下结论:

(1)广义Kelvin 蠕变损伤模型考虑了材料塑性和损伤特性，可以表征岩石的非线性和加速蠕变阶段.

(2)采用粒子群算法、模拟退火算法与FLAC3D 相结合的智能方法，对已有试验数据进行反演，该模型能较好模拟低应力下岩石的两阶段蠕变和高应力下岩石的三阶段蠕变效应.

(3)流变曲线越复杂，反演算法收敛速度越慢.但只要选定合适的参数值，反演算法在40 代左右就可以收敛到全局最优解.

［1］ 高赛红，曹平，汪胜莲，等. 改进的岩石非线性黏弹塑性蠕变模型及其硬化黏滞系数的修正［J］. 煤炭学报，2012，37(6):936-943.GAO Saihong，CAO Ping，WANG Shenglian，et al.Improved nonlinear viscoelasto-plastic rheological model of rock and its correction of hardening coefficient of viscosity［J］. Journal of China Coal Society，2012，37(6):936-943.

［2］ 陈卫忠，王者超，伍国军，等. 盐岩非线性蠕变损伤本构模型及其工程应用［J］. 岩石力学与工程学报，2007，26(3):467-472.CHEN Weizhong，WANG Zhechao，WU Guojun，et al.Nonlinear creep damage constitutive model of rock salt and its application to engineering［J］. Chinese Journal of Rock Mechanics and Engineering，2007，26(3):467-472.

［3］ 朱昌星，阮怀宁，朱珍德，等. 岩石非线性蠕变损伤模型的研究［J］. 岩土工程学报，2008，30(10):1510-1513.ZHU Changxing，RUAN Huaining，ZHU Zhende，et al.Non-linear rheological damage model of rock［J］.Chinese Journal of Geotechnical Engineering，2008，30(10):1510-1513.

［4］ CHAN K S，BRODSKY N S，FOSSUM A F，et al.Damage-induced non-associated inelastic flow in rock salt［J］. International Journal of Plasticity，1994，10(6):623-642.

［5］ 杨圣奇，徐鹏. 一种新的岩石非线性流变损伤模型研究［J］. 岩土工程学报，2014，36(10):1846-1854.YANG Shenqi，XU Peng. A new nonlinear rheological damage model for rock［J］. Chinese Journal of Geotechnical Engineering，2014，36(10):1846-1854.

［6］ 杨文东. 坝基软弱岩体的非线性蠕变损伤本构模型及其工程应用［D］. 济南:山东大学岩土与结构工程研究中心，2008.

［7］ 黄明，刘新荣，邓涛. 基于含水劣化特性的隧道围岩时效变形数值计算［J］. 岩土力学，2012，33(6):1876-1882.HUANG Ming，LIU Xinrong，DENG Tao. Numerical calculation of time effect deformations of tunnel surrounding rock in terms of water degradation［J］.Rock and Soil Mechanics，2012，33(6):1876-1882.

［8］ 袁海平，曹平，许万忠，等. 岩体黏弹塑性本构关系及改进Burgers 蠕变模型［J］. 岩土工程学报，2006，28(6):796-799.YUAN Haiping，CAO Ping，XU Wanzhong，et al.Visco-elastic-plastic constitutive relationship of rock and modified Burgers creep model［J］. Chinese Journal of Geotechnical Engineering，2006，28(6):796-799.

［9］ Itasca Consulting Group，Inc. Fast Lagrangian analysis of continua in three dimensions (version 3.0):user's manual［R］. Minnesota: Itasca Consulting Group，Inc.，2003.

［10］ 史峰，王辉，胡斐，等. Matlab 智能算法30 个案例分析［M］. 北京:北京航空航天大学出版社，2011:101-134.

［11］ 李丽，牛奔. 粒子群优化算法［M］. 北京:冶金工业出版社，2009:62-83.

［12］ 黄明. 含水泥质粉砂岩蠕变特性及其在软岩隧道稳定性分析中的应用研究［D］. 重庆:重庆大学土木工程学院，2010.

［13］ 蒋昱州，张明鸣，李良权. 岩石非线性黏弹塑性蠕变模型研究及其参数识别［J］. 岩石力学与工程学报，2008，27(4):832-839.JIANG Yuzhou，ZHANG Mingming，LI Liangquan.Study on nonlinear viscoelasto-plastic creep model of rock and its parameter identification［J］. Chinese Journal of Rock Mechanics and Engineering，2008，27(4):832-839.

［14］ 陈裕民. 锦屏一级水电站建基岩体力学参数选取研究［D］. 成都:成都理工大学环境与土木工程学院，2010.

［15］ 刘衍民，牛奔. 新型粒子群算法理论与实践［M］.北京:科学出版社，2013:45-68.