两阶段耗能屈曲约束支撑体系减震效果分析

潘 毅， 耿鹏飞， 郭阳照，3， 易路行

(1. 西南交通大学土木工程学院，四川 成都610031;2. 西南交通大学交通隧道工程教育部重点实验室，四川成都610031;3. 四川省建筑科学研究院，四川 成都610081)

屈曲约束支撑(buckling restrained brace，BRB)作为一种新型的消能支撑，克服了普通钢支撑受压屈曲的弊病，具有稳定的滞回性能和卓越的耗能能力［1-3］，是目前建筑减震控制中应用最广泛的减震装置之一.屈曲约束支撑分为普通耗能型屈曲约束支撑和早耗能型屈曲约束支撑(下文分别简称为HN-BRB 和ZN-BRB).HN-BRB 的芯材为普通钢，其屈服承载力和屈服位移较大，控制在中震或大震下屈服耗能，而在小震下保持弹性;ZN-BRB 的芯材为低屈服点钢，其屈服承载力和屈服位移小，在小震下即可发生屈服耗能，且其延性良好，可保证小震和中震下具有良好的耗能性能［4］，其变形能力可满足大震下结构的变形需求［5-6］.

目前，建筑工程中采用屈曲约束支撑进行减震控制的常规做法是将HN-BRB 安装在主体结构上形成减震体系(下文简称常规BRB 减震体系).HN-BRB 在小震下保持弹性，增大结构刚度来控制结构变形，而在中震或大震下屈服耗能，耗散结构的地震输入能量，减小结构的地震反应. 但在高烈度区，这样的设计结构刚度较大，受力较大会增加材料用量，且需使用较大吨位的支撑，对支撑连接节点的要求也较为苛刻，不利于结构的抗震性能.因此，本文提出两阶段耗能屈曲约束支撑减震体系(下文简称两阶段BRB 减震体系)，即将ZN-BRB和HN-BRB 都安装在主体结构上，二者在地震中先后屈服，分两阶段启动耗能，并结合工程算例，按照小震设防阶段侧向变形水平相同的原则，设计常规屈曲约束支撑减震体系与两阶段耗能屈曲约束支撑减震体系.在此基础上选取层间位移、基底剪力、柱设计轴压比和构件塑性铰状态等作为性能指标，对比两阶段BRB 减震体系的减震效果.

1 两阶段BRB 减震体系的工作原理

在两阶段BRB 减震体系中，ZN-BRB 在小震时屈服耗能，衰减结构的地震反应，利于控制结构变形，节约材料用量.HN-BRB 在中震或大震时屈服，和前者共同耗能，保护主体结构.

动力方程为

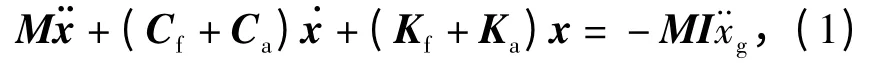
式中:M 为结构质量矩阵;

I 为单位列向量;

Cf为主体结构阻尼矩阵;

Ca为附加阻尼矩阵;

Kf为主体结构刚度矩阵;

Ka为附加刚度矩阵.

小震时，Ca、Ka均不等于0，但Ca仅包含ZN-BRB的附加阻尼，Ka包含ZN-BRB 的附加刚度和HN-BRB 的弹性刚度;中震或大震时，Ca和Ka均不等于0，且Ca包含2 种BRB 的附加阻尼，Ka包含两种BRB 的附加刚度.

2 设计模型

算例采用6 层RC 框架结构，其各层平面布置如图1 所示，常见于商场、图书馆等建筑.首层层高5.1 m，其他层层高均为3.3 m，总高度21.6 m.设防烈度为8 度(0.3g，g 为重力加速度)，地震分组为第二组，Ⅱ类场地，抗震等级为二级. 竖向荷载(不含结构自重):楼面均布恒载为3.7 kN/m2，楼面均布活载为2 kN/m2，屋面均布恒载为4.5 kN/m2，屋面均布活载为0.5 kN/m2，楼面中间框架梁均布恒载为9.5 kN/m，楼面边框架梁均布恒载为6.5 kN/m，屋面框架边梁恒载为3.3 kN/m.

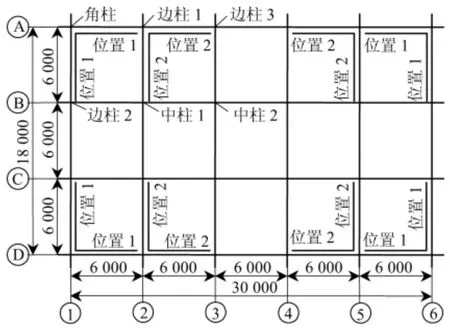
图1 结构平面及屈曲约束支撑布置Fig.1 Layout of structure and BRB

2.1 纯框架结构设计

按《建筑抗震设计规范》(GB50011—2010)［7］(下文简称《抗规》)中“小震不坏，中震可修，大震不倒”的设防水准进行抗震设计.减震体系设计采用目前普遍的方法［8］，即首先仅考虑竖向荷载和风荷载设计纯框架结构，然后附加屈曲约束支撑进行减震体系设计.本算例所设计的纯框架结构中框架梁、柱的截面尺寸和混凝土强度等级如表1 所示.

2.2 常规BRB 减震体系设计

将HN-BRB 安装在上述的纯框架结构上，形成常规BRB 减震体系，根据文献［9-10］确定HN-BRB的附加刚度时，各层名义抗侧刚度比k=KBRB/Kf控制为1 ～2，各层HN-BRB 的吨位和数量等参数见表2. 采用单斜撑型布置形式，遵循文献［1，11］中的原则，BRB 的布置应尽量均匀、对称和分散，可将其布置在结构外围用以改善结构扭转，且结构沿竖向无刚度突变，平面布置如图1 所示.第1 ～4 层，大吨位的布置在“位置1”，小吨位的布置在“位置2”，第5、6 层布置在“位置1”，布置BRB 的立面如图2 所示. 小震下变形验算满足后，进行结构设计.

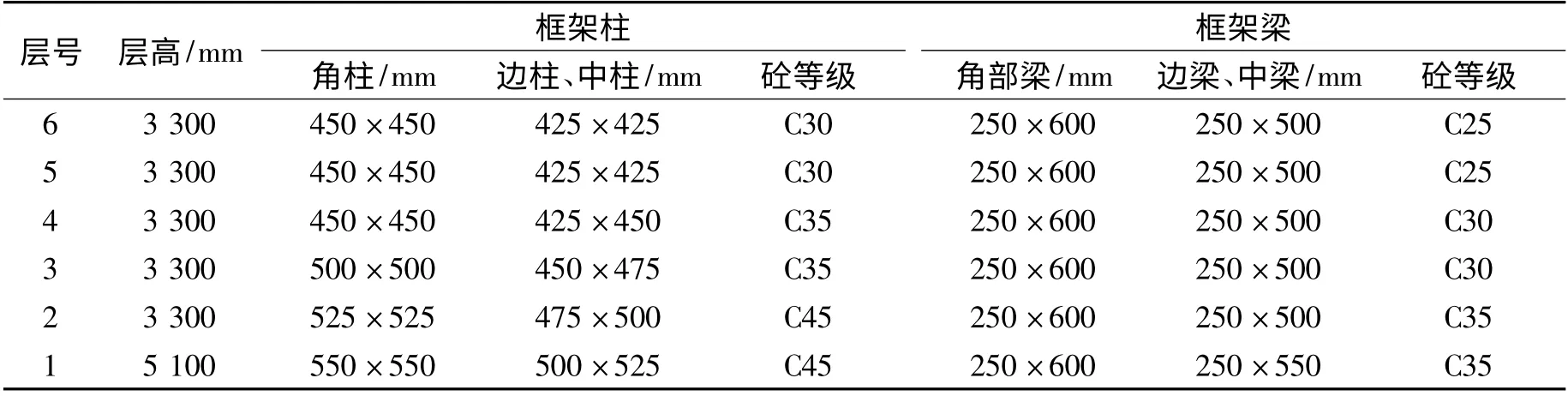
表1 梁、柱截面尺寸及混凝土强度等级Tab.1 Cross-section sizes of beams and columns and the strenth grade of concrete

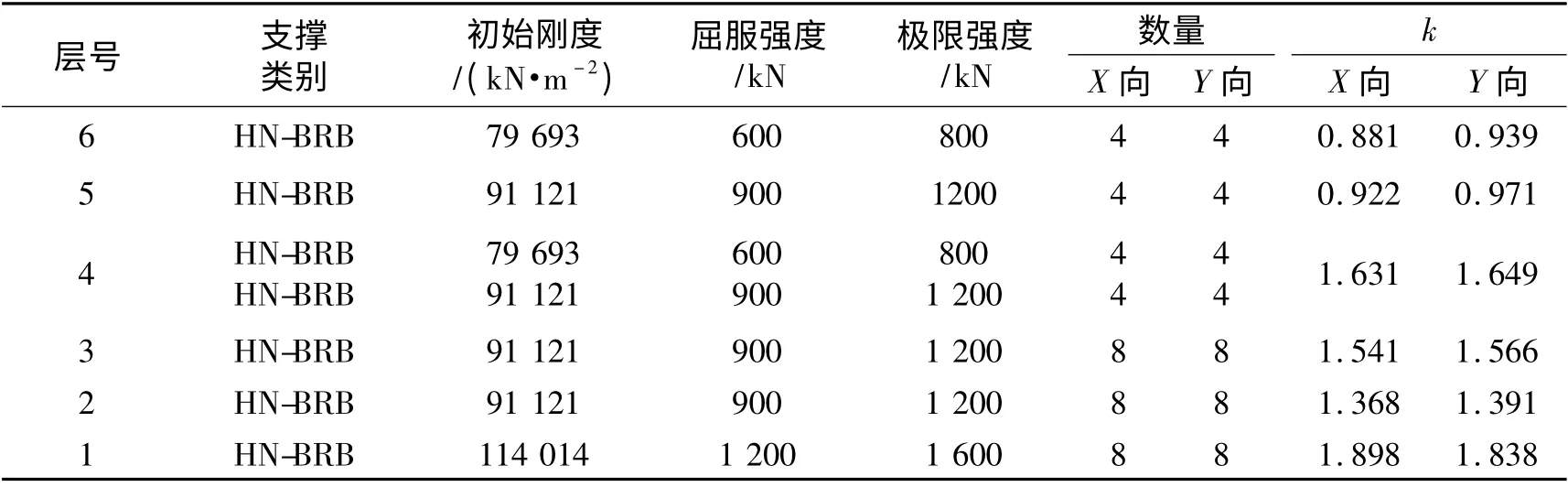
表2 常规BRB 减震体系屈曲约束支撑参数Tab.2 RBB's parameters of general BRB damping system

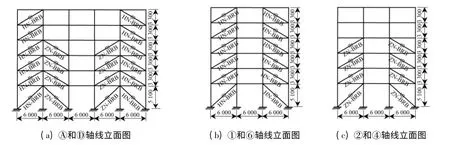
图2 屈曲约束支撑立面布置图Fig.2 Vertical view of layout of BRB

2.3 两阶段BRB 减震体系设计

将ZN-BRB 和HN-BRB 都安装在上述纯框架结构上形成两阶段BRB 减震体系，每层屈曲约束支撑的名义抗侧刚度比、数量及吨位等参数见表3.仍采用单斜撑型布置，如图 1 所示.第1 ～4 层，HN-BRB 布置在“位置1”，ZN-BRB 布置在“位置2”，第5、6 层ZN-BRB 布置在“位置1”，布置立面同图2. 采用双线性恢复力模型［12］，通过反应谱分析，使用等效线性化方法迭代计算来确定ZN-BRB 在小震下的附加阻尼比和附加等效刚度［11，13］.小震作用下变形验算满足后，进行结构设计.需说明的是，小震设防阶段两种减震体系的侧向变形设计为相同，梁柱截面尺寸是迭代调整 的结果，所以柱子截面尺寸种类略多.

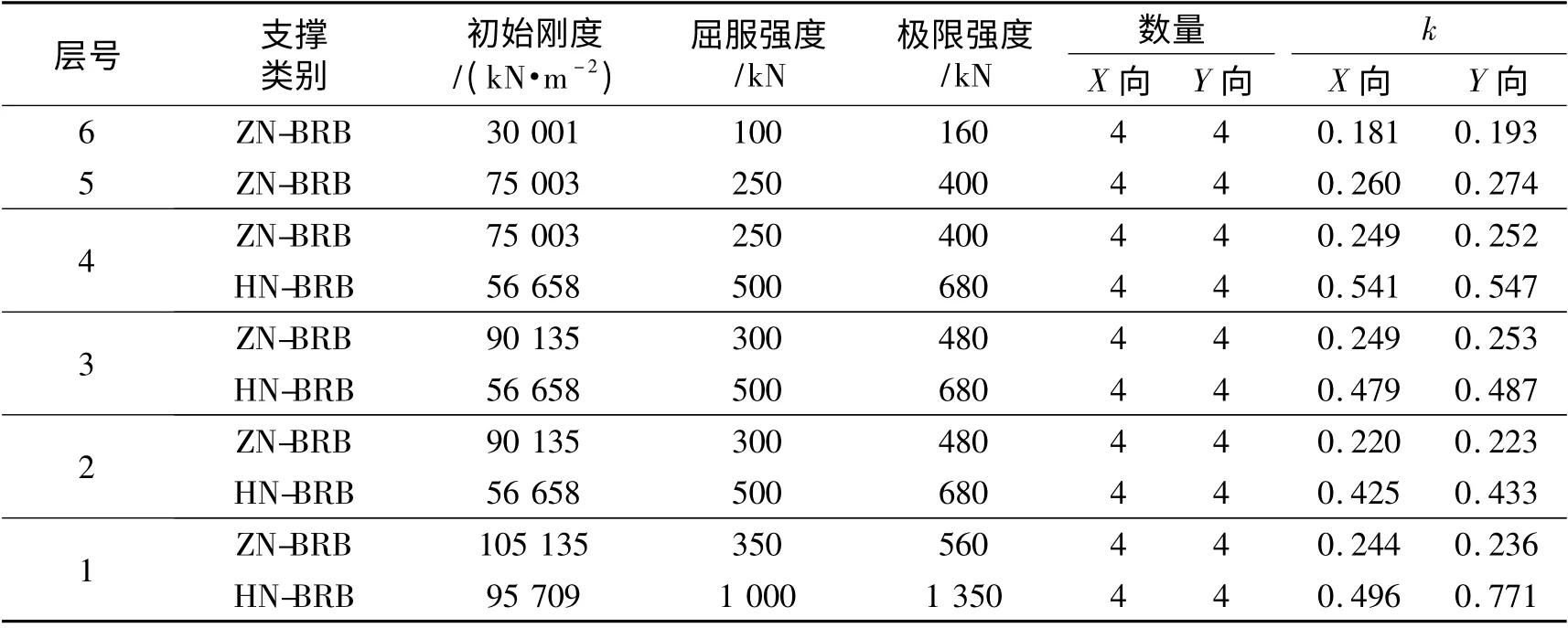
表3 两阶段BRB 减震体系中屈曲约束支撑参数Tab.3 RBB's parameters of two-stage BRB damping system

3 数值分析模型

采用SAP2000 分别建立上述纯框架结构、常规BRB 减震体系和两阶段BRB 减震体系的数值模型.

3.1 主体框架的模拟

材料的弹塑性本构模型是弹塑性时程分析的核心，它综合反映混凝土构件的刚度、强度、延性和耗能能力等力学特性［14］. 上述3 种模型均为杆单元模型，混凝土采用Takeda 模型模拟其弹塑性滞回行为.结构构件屈服前后的行为用离散的塑性铰来模拟，本文采用FEMA356［15］中的梁端弯矩塑性铰和柱端轴力弯矩相关铰，并将这两种铰指定给SAP2000 模型中的梁、柱单元.

结构阻尼采用质量和刚度比例阻尼(即Rayleigh 阻尼)，它假设阻尼矩阵与质量矩阵、刚度矩阵成正比，即

3.2 屈曲约束支撑的模拟

屈曲约束支撑用非线性连接单元模拟，其恢复力采用Bouc-Wen 滞回模型［16］，可对各种光滑的滞回曲线近似描述，表达如下:

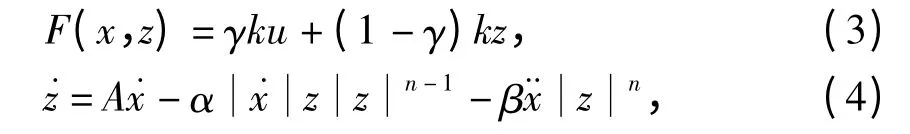
u 为外界激励;

z 为Bouc-Wen 滞回非线性恢复力，其特性取决于材料特性、响应幅值和结构特性;

A、n、α、β 均为滞回常数.

线弹性工况中ZN-BRB 有效刚度设置为附加等效刚度，附加阻尼比设置为5%. 非线性工况中分别按表2 和表3 逐个输入ZN-BRB 和HN-BRB的初始刚度、屈服承载力，屈服后刚度比和屈服指数分别取0.03 和2.00.

3.3 地震波的选取

按《抗规》对地震波频谱特性的要求，选用Ⅱ类场地上4 条实际记录的地震波，即Elcentro 波、Taft 波、唐山波1(北京饭店东西向)、唐山波2(北京饭店南北向)和一条按场地条件生成的人工波，分别按X、Y 向单方向输入. 地震动有效持续时间均在结构基本周期的5 ～10 倍以上.

4 两阶段BRB 减震体系与常规BRB减震体系的减震效果对比

4.1 模态周期

3 种模型的前3 阶模态周期如表4 所示.其中FRAME 代表纯框架结构，N-BRBF 代表常规BRB减震体系，T-BRBF 代表两阶段BRB 减震体系.

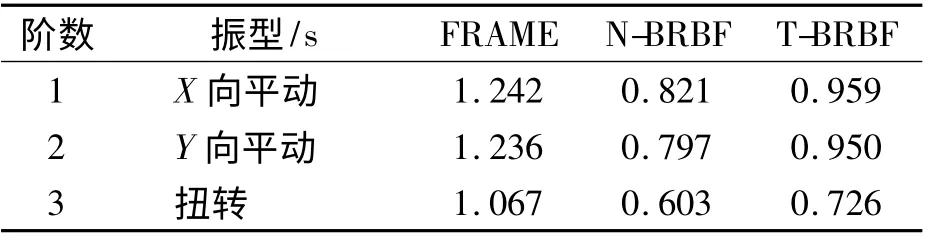
表4 3 种模型的前3 阶模态周期Tab.4 First three model periods of the three kinds of models

由表4 可见，T-BRBF 的周期明显大于N-BRBF，主体虽相同，但采用的屈曲约束支撑不同，使得T-BRBF 的刚度相对于N-BRBF 明显降低，前3 阶周期分别增加了16.80%、19.20%、20.39%，表明T-BBRF 刚度减小，则地震作用降低.FRAME、N-BRBF、T-BRBF 的周期比(即结构第一扭转周期与结构第一平动周期之比)分别为0.859、0.734、0.757，这表明安装屈曲约束支撑有助于改善结构扭转性能.

4.2 小震下分析结果对比

(1)层间变形

小震下反应谱分析可得3 个结构的层间变形，如图3 所示.纯框架结构的层间位移角在1/340 左右，远大于允许值1/550. 而N-BRBF 和T-BRBF的层间位移角显著减小，且2 者层间位移角最大相差3.4%.N-BRBF 的X、Y 向最大层间位移角分别为1/572、1/561，T-BRBF 的X、Y 向最大层间位移角分别为1/571、1/554，且均发生在第2 层，N-BRBF和T-BRBF均满足《抗规》中侧向变形的要求.

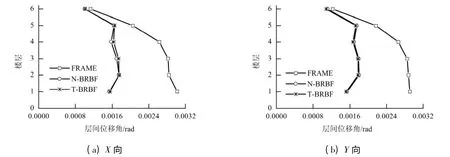
图3 多遇地震作用下反应谱分析的层间位移角Fig.3 Story drift angle of response spectrum analysis under the frequent earthquakes

(2)基底剪力

小震下反应谱分析和线弹性时程分析的基底剪力峰值如表5 所示.相对于N-BRBF，T-BRBF 的基底剪力大幅度降低，其中反应谱分析的基底剪力降低近30%.线弹性时程分析中，Taft 波降幅最大，达到50%，Elcentro 波降幅最小，但X、Y 向的降幅也均超过20%.

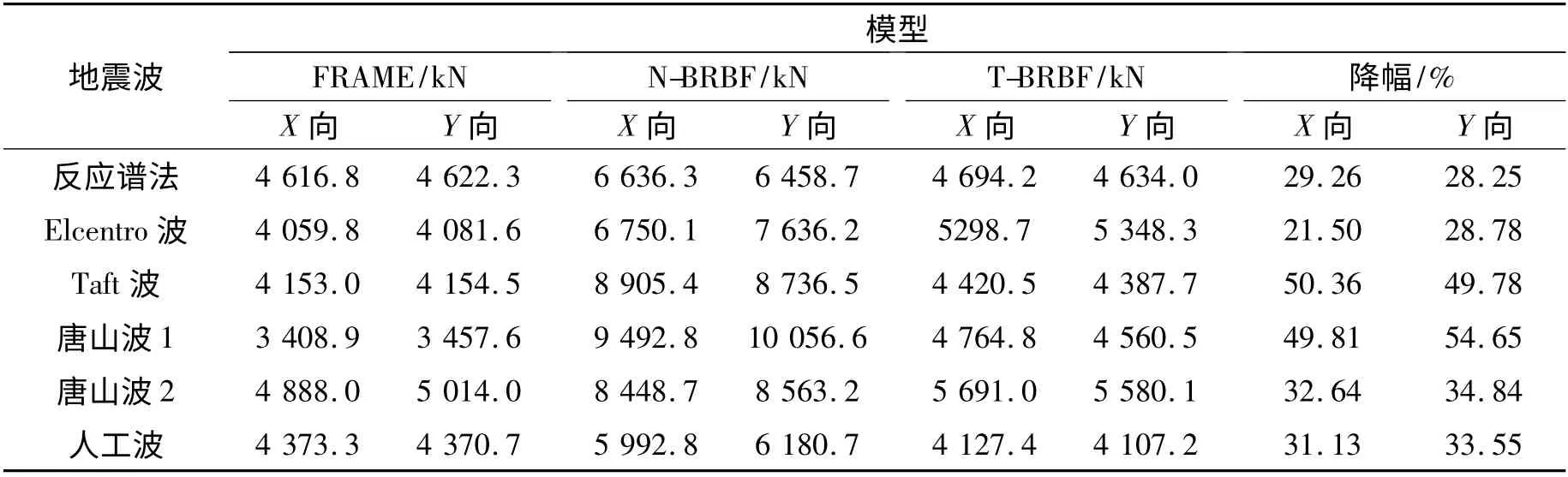
表5 多遇烈度地震作用下基底剪力峰值Tab.5 Peak values of foundation shear force under frequent earthquakes

因此，多遇地震时T-BRBF 的受力比N-BRBF低，与4.1 节的分析吻合，这有利于控制结构变形和节约配筋.

(3)设计轴压比

首层角柱、边柱和中柱的设计轴压比如表6 所示.N-BRBF 和T-BRBF 均满足柱轴压比限值，但是T-BRBF 柱的设计轴压比更低，结构延性更好，提高了结构的抗震性能. 因此，在轴压比相同的前提下，T-BRBF 可以用相对较小的截面，更节约材料.

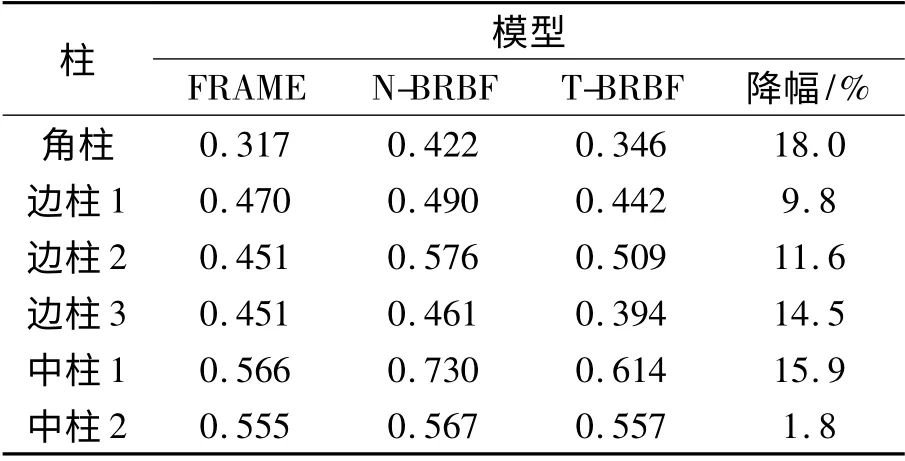
表6 柱的设计轴压比Tab.6 Designed axial compression ratio of columns

4.3 大震下的分析结果对比

采用直接积分法求解结构动力微分方程，以此分析大震下的弹塑性时程，积分方法采用HHT 法.

(1)基底剪力

基底剪力时程峰值如表7 所示.相比N-BRBF，T-BRBF 的基底剪力降低，其中降幅最大是唐山波1，达到28%，降幅最小是Taft 波，超过了22%.故T-BRBF 在大震下的受力显著减小，结构的安全性提高.

(2)层间变形

在唐山波2 作用下，结构的层间位移角如图4所示.3 个模型的薄弱层均在第2 层，纯框架结构的最大层间位移角在1/60 左右，逼近弹塑性位移角限值1/50，结构濒临倒塌.而N-BRBF 和T-BRBF的侧向变形大大减小，二者最大层间位移角介于1/120-1/130，且后者略小于前者.

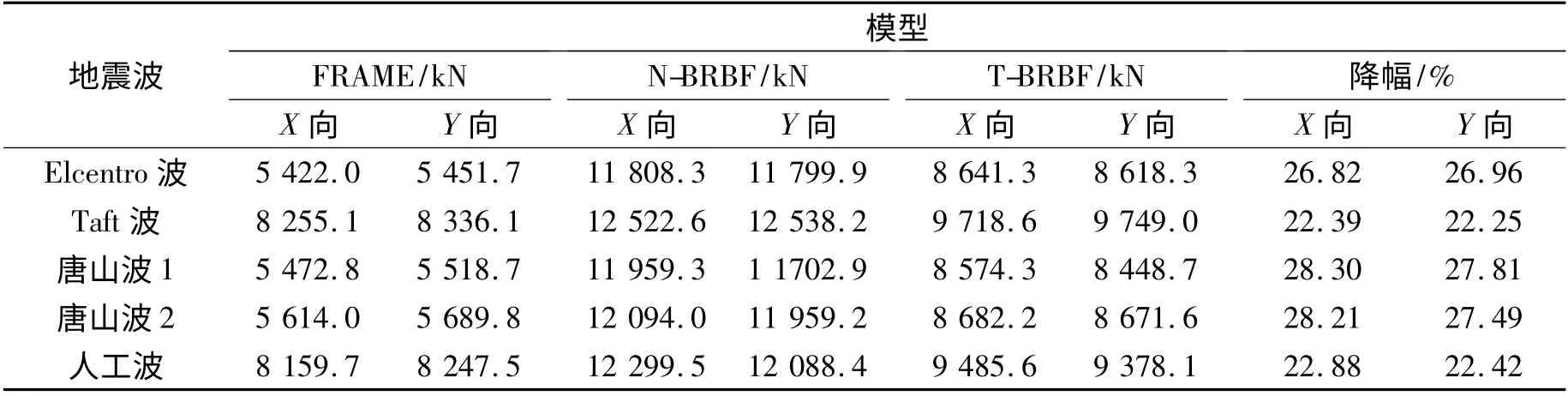
表7 罕遇地震作用下弹塑性分析的基底剪力峰值Tab.7 Peak values of foundation shear force under rare earthquakes

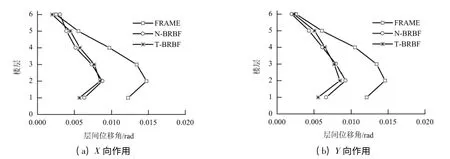
图4 唐山波2 作用下的弹塑性层间位移角Fig.4 Elastic-plastic story drift angle under the 2 nd Tangshan wave

(3)梁和柱塑性铰的状态

在唐山波2 工况下，3 种模型的梁和柱塑性铰的状态和数量如表8 所示.纯框架结构塑性发展程度较高，且柱端出铰较快，而N-BRBF 和T-BRBF主体构件塑性铰的发展大大推迟，主体构件的破坏程度显著减轻，且柱的塑性铰发展明显滞后于梁，属“梁铰模式”.同时，T-BRBF主体构件塑性铰的发展比N-BRBF 进一步推迟，其抗震性能相对提高.

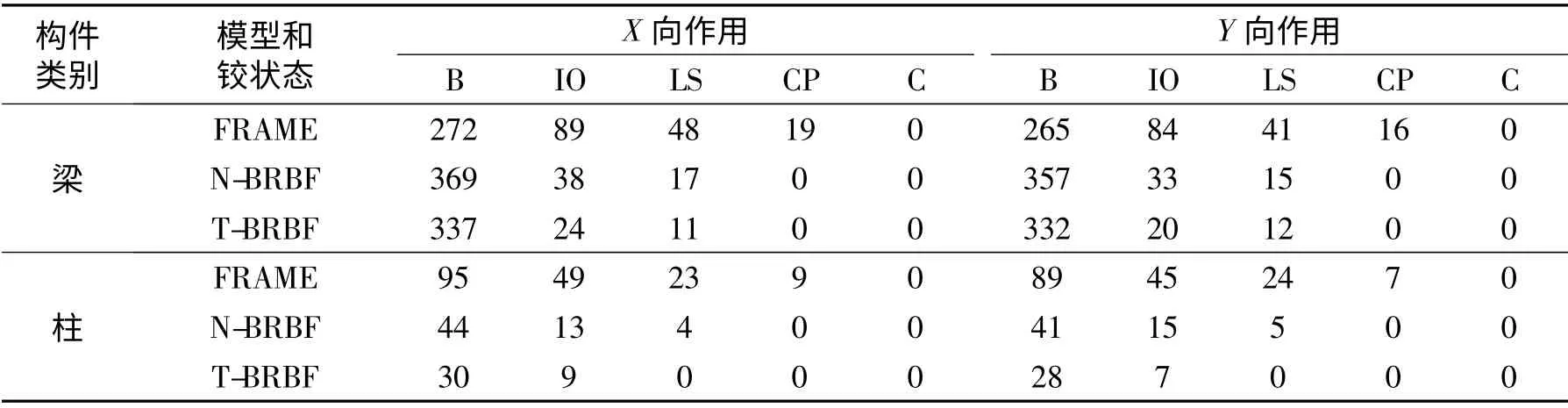
表8 唐山波2 作用下结构铰的状态Tab.8 State of hinges under the 2nd Tangshan wave

(4)屈曲约束支撑的滞回状况

在平面图首层右下方X、Y 向的“位置1”和“位置2”处，屈曲约束支撑在Taft 波作用下的滞回曲线如图5 所示.由图5 可知，相对于N-BRBF，TBRBF 中屈曲约束支撑出力减小超过20%，其一减小了连接节点受力，降低了对节点的要求;其二，降低了框架柱的附加轴力，提高了框架柱的延性，改善了结构的抗震性能. 同时，T-BRBF 的屈曲约束支撑的滞回曲线较N-BRBF 的更加圆润饱满，所以T-BRBF中屈曲约束支撑耗能能力发挥得更充分，且ZN-BRB 伸长率最大约为0.66%，远小于软钢的伸长率，满足大震下的变形需求.

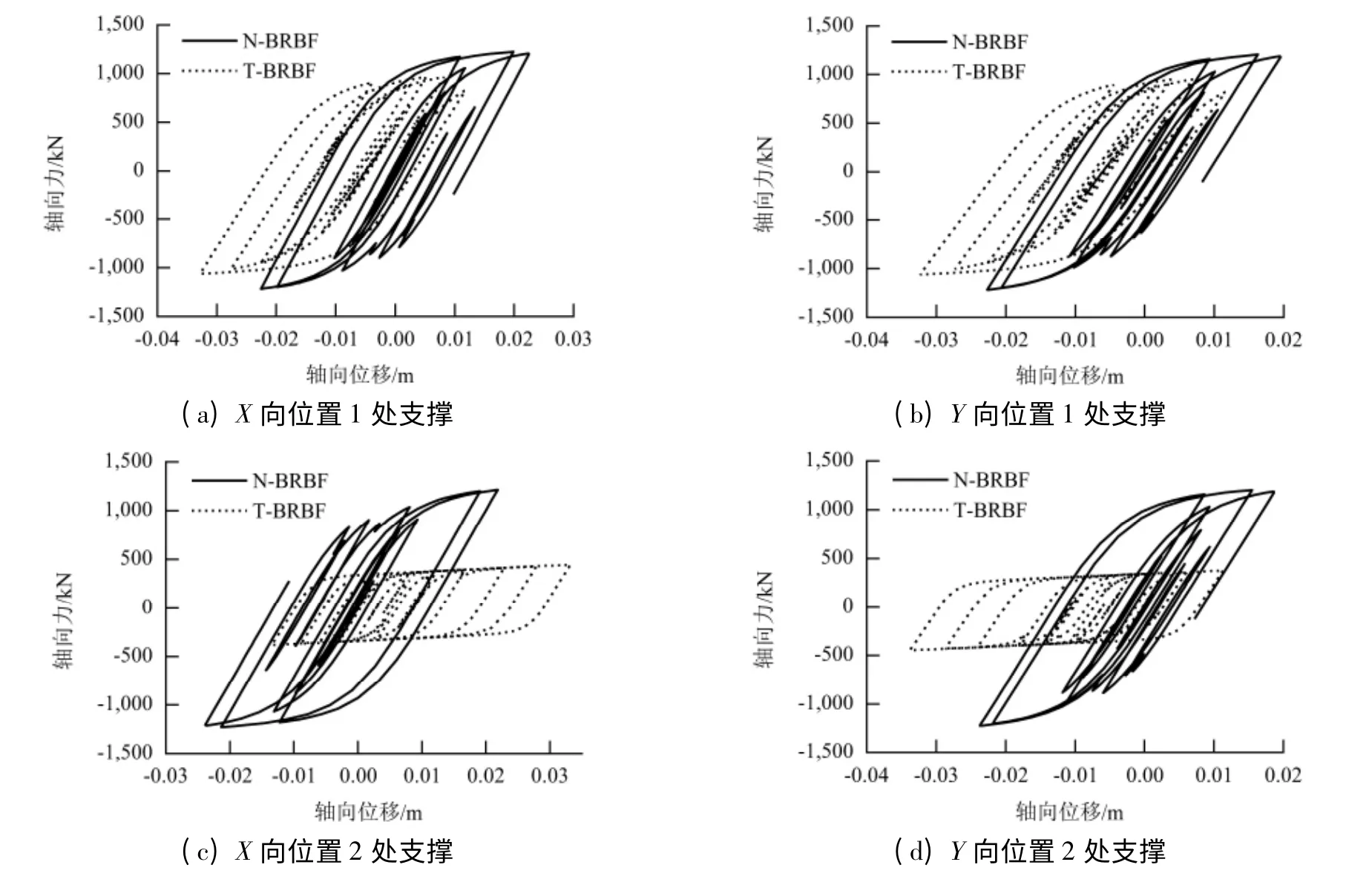
图5 Taft 波作用下屈曲约束支撑的滞回曲线Fig.5 Hysteretic curves of bucking restrained braces under Taft ground motion

4.4 屈服机制

各地震波作用下，N-BRBF 和T-BRBF 两种减震体系中的屈曲约束支撑在地震中均是先于主体结构发生屈服.图6 给出了Taft 波大震下T-BRBF在图1 中Ⓐ榀框架的塑性发展过程. 地震中ZN-BRB 最早屈服(图6(a))，HN-BRB继而屈服(图6(b))，主体构件最后屈服出铰(图6(c))，图6(d)给出了时程结束时该榀框架的塑性状态.因此，实现了ZN-BRB 和HN-BRB 在地震中分两阶段屈服耗能，从而保护主体结构.

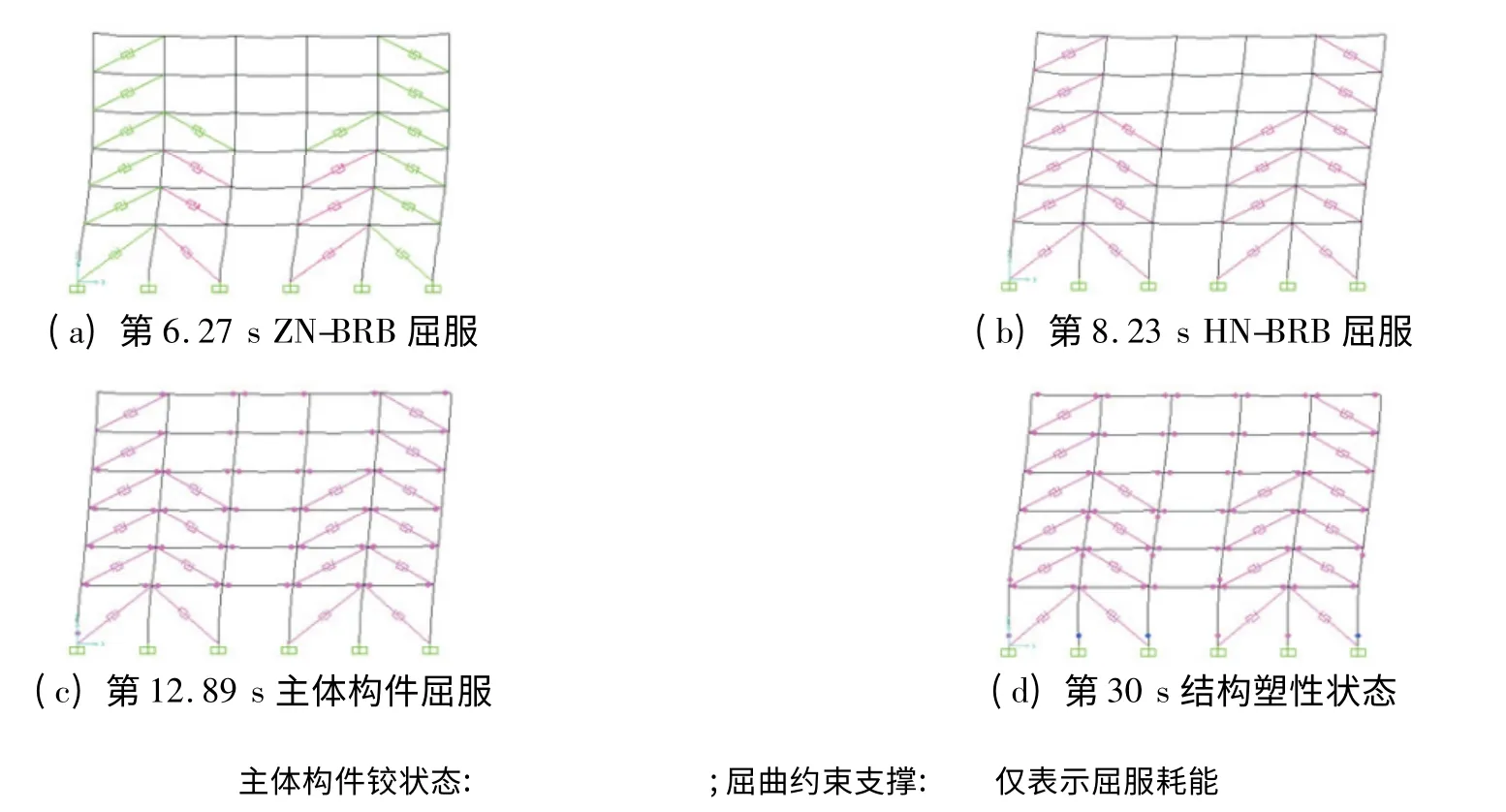
图6 T-BRBF 在X 向Taft 波大震下的塑性发展过程Fig.6 Plasticity development process of T-BRBF under the X direction rare earthquakes of Taft ground motion

5 结 论

结合高烈度区工程算例，分析了常规屈曲约束支撑减震体系和两阶段耗能屈曲约束支撑减震体系的减震效果.主要结论有:

(1)与常规屈曲约束支撑减震体系相比，两阶段耗能减震体系的刚度降低，地震作用明显减小，小震和大震下结构地震作用降低均超过20%，而且塑性铰的发展得到推迟，抗震性能有效提高.

(2)两阶段耗能屈曲约束支撑的吨位明显降低、出力减小，所以连接节点的受力降低，提高了其可靠性，且柱附加轴力的降低亦改善了结构的延性.

(3)早耗能型和普通耗能型屈曲约束支撑联合使用，二者在地震中先后屈服，实现了分两阶段启动耗能，亦符合“多道防线”的抗震设防思想.

［1］ 周云. 防屈曲耗能支撑结构设计及应用［M］. 北京:中国建筑工业出版社，2007:6-11.

［2］ XIE Q. State of the art of buckling restrained braces in asia［J］. Journal of Construction Steel Research，2005，61(6):27-32.

［3］ 汪家铭，中岛正爱，陆烨(译). 屈曲约束支撑体系的应用于研究进展(Ⅰ)［J］. 建筑钢结构进展，2005，7(1):1-12.WANG Chiaming，NAKASHIMA Masayoshi，LU Ye.The practice and research development of bucklingrestrained braced frames(Ⅰ)［J］. Progress in Building Structures，2005，7(1):1-12.

［4］ 周云. 耗能减震加固技术与设计方法［M］. 北京:科学出版社，2006:40-51.

［5］ 王佼佼，石永久，严红，等. 低屈服点全钢防屈曲支撑抗震性能试验研究［J］. 土木工程学报，2013，46(10):9-16.WANG Jiaojiao，SHI Yongjiu，YAN Hong，et al.Experimental study on the seismic behavior of all-steel buckling-restrained brace with low yield point［J］.China Civil Engineering Journal，2013，46(10):9-16.

［6］ 李国强，胡宝林，孙飞飞，等. 国产TJI 型屈曲约束支撑的研制与试验［J］. 同济大学学报:自然科学版，2011，39(5):631-636.LI Guoqiang， HU Baolin， SUN Feifei， et al.Development and experiment study on domestic TJI buckling-restrained brace［J］. Journal of Tongji University:Natural Science，2011，39(5):631-636.

［7］ 中华人民共和国住房和城乡建设部. GB50011—2010 建筑抗震设计规范［S］. 北京:中国建筑工业出版社，2010:1-3.

［8］ 高向宇，郑腾龙，黄海涛，等. 用防屈曲支撑改进钢框架-支撑结构抗震性能的设计方法［J］. 北京工业大学学报，2010，36(9):1206-1214.GAO Xiangyu，ZHANG Tenglong，HUANG Haitao，et al. The design method for improving the aseismatic performance of concentrically braced steel frames with buckling-restrained brace［J］. Journal of Beijing University of Technology，2010，36(9):1206-1214.

［9］ 朱江，李帼昌，马传正. 屈曲约束支撑-钢筋混凝土框架结构的设计与分析［J］. 建筑结构，2012，42(12):54-58.ZHU Jiang，LI Jinchang，MA Chuanzheng. Analysis and design on buckling restrained braces-reinforced concrete frame structures［J］. Building Structure，2012，42(12):54-58.

［10］ 赵瑛，郭彦林. 防屈曲支撑框架设计方法研究［J］.建筑结构，2010，40(1):38-43.ZHAO Ying，GUO Yanlin. Research on design method of buckling restrained braced frames［J］. Building Structure，2010，40(1):38-43.

［11］ 潘鹏，叶列平，钱佳茹，等. 建筑结构消能减震设计与案例［M］. 北京:清华大学出版社，2014:74-75.

［12］ 周云. 金属耗能减震结构设计［M］. 武汉:武汉理工大学出版社，2006:59-60.

［13］ 王奇，干刚. 基于线性化等效方法的消能减震结构有效附加阻尼比计算［J］. 建筑结构学报，2012，4(1):46-52.WANG Qi， GAN Gang. Calculation of effective additional damping ratio of energy dissipation structure based on linear equivalent method［J］. Journal of Building Structures，2012，4(1):46-52.

［14］ 李爱群，丁幼亮. 工程结构抗震分析［M］. 北京:高等教育出版社，2010:124.

［15］ Federal Emergency Management Agency. Prestandard and commentary for the seismic rehabilitation of buildings［S］. Washington:FEMA356，2000:21-22.

［16］ 李鸿光，何旭，孟光. Bouc-Wen 滞回系统动力学特性的仿真研究［J］. 系统仿真学报，2004，16(9):2009-2011.LI Hongguang，HE Xu，MENG Guang. Numerical simulation for dynamic characteristics of Bouc-Wen hysteretic system［J］. Journal of System Simulation，2004，16(9):2009-2011.