大跨度钢斜拉桥制造误差的传播及其效应特性

张清华， 黄 灿， 卜一之， 李 乔

(1. 西南交通大学土木工程学院，四川成都610031;2. 中交第二航务工程局有限公司技术中心，湖北 武汉430040)

实施有效的施工控制是大跨度斜拉桥高质量 修建的前提［1-9］.施工控制的首要任务是控制施工误差，使最终的实际成桥状态逼近理想的目标状态.而对于误差及其效应特性的深刻认识是实现高质量施工控制的基础和关键.近年来千米级超大跨度斜拉桥迅速发展，该类桥梁通常采用钢箱梁，结构纤柔、构件数量多、施工期长、施工工序复杂、误差调控困难、施工期结构的安全性问题突出，给施工控制提出了质量保障和风险抑制的双重挑战［8-9］.

国内外学者对斜拉桥的施工控制方法进行了深入研究，结果表明［8-15］:相对于传统的部分过程控制方法而言，全过程自适应控制是超大跨度斜拉桥较为适用的控制方法. 从全过程控制的角度出发，斜拉桥成桥状态误差的形成过程，本质上属于多种误差因素导致的误差效应在其整个施工过程中耦合影响并不断传播的过程，阐明误差传播及其效应特性是实现最优控制的前提.尽管全过程控制方法在多座大跨度斜拉桥施工控制中得到了成功应用，但目前关于全过程控制条件下误差的传播机理仍缺乏系统、深入的研究［9-11］.

本文旨在研究构件制造误差在超大跨度钢箱梁斜拉桥施工全过程中的形成和传播过程，建立误差效应传播方程，并以典型超大跨度斜拉桥为研究对象，探究重要构件制造误差对于线形和索力状态误差的效应特性.

1 全过程控制的误差来源

对大跨度钢斜拉桥而言，施工误差、测量误差和环境误差是导致其主梁线形、斜拉索索力和索塔塔偏等状态误差的主要因素.根据全过程控制的实施过程、实现方式和误差间的相互关系，可将全过程控制条件下的误差分为“原始误差”和“衍生误差”两大类，前者主要包括物理参数误差和由构件制造和拼装误差组成的构件几何形态误差.原始误差是导致施工全过程中状态误差的主要原因.衍生误差则是指由原始误差导致的结构状态误差，实质上是原始误差的具体体现和实际效应，主要包括主梁线形误差、斜拉索索力误差和索塔塔偏误差等.

构件制造、安装误差及其效应控制是全过程控制最重要的控制内容.本文中以主梁节段和斜拉索为例，说明制造误差的组成要素. 对于主梁节段而言，制造误差主要包括三部分:(1)梁段自身的无应力长度误差;(2)梁段间的无应力角度误差;(3)主梁节段索锚点位置误差.

斜拉索制造误差主要指其长度的制造误差.主梁和索塔索锚点位置的制造误差导致斜拉索的安装误差，其误差效应的分析方法和斜拉索制造误差的分析方法相同;主梁节段间拼装误差效应的分析方法则与主梁节段间无应力角度制造误差效应的分析方法相同.

全过程控制通过控制构件的无应力状态实现控制目标，而关键施工阶段的主梁线形和斜拉索索力状态误差则是评判控制质量的重要依据. 因此，建立结构状态误差与构件制造误差之间的关系至关重要.同时，阐明制造误差效应在施工全过程中的传播机理，是进行科学、有效的误差调控，进而实现施工控制目标的基本前提.下面就典型构件的制造误差效应在施工全过程中的传播机理进行研究，建立制造误差效应的传播方程;在此基础上以典型的超大跨度钢箱梁斜拉桥——苏通大桥为研究对象，采用建立的误差传播方程探讨制造误差导致的结构状态误差的形成及其传播过程，以及关键构件制造误差的效应特性.

2 误差效应传播方程的建立

2.1 全过程控制条件下的几何非线性平衡方程

构件无应力形态的确定方法可参见文献［9］，限于篇幅，此处不再赘述.为不失一般性，以杆系单元安装时刻的几何形态作为计算起点，设单元的无应力长度为l0，其i 端和j 端的无应力曲率分别为ki0和kj0.该阶段单元的初始长度为l(单元初始安装阶段则为l0)，所受轴力为N，荷载作用下结点位移分别为{¯ui，¯vi，¯θi}和{¯uj，¯vj，¯θj}. 其中，¯u 为局部坐标系x'轴方向的结点位移，¯v 为y'轴方向的结点位移，¯θ 为结点角位移，见图1.

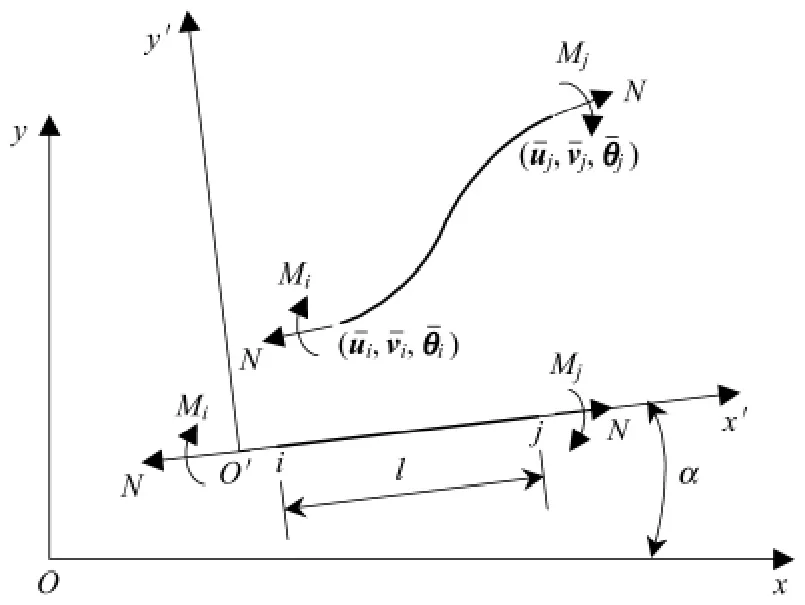
图1 杆系单元变形Fig.1 Deformation of trussing element

单元几何刚度矩阵(即初始应力刚度矩阵，与单元的初始应力水平有关)

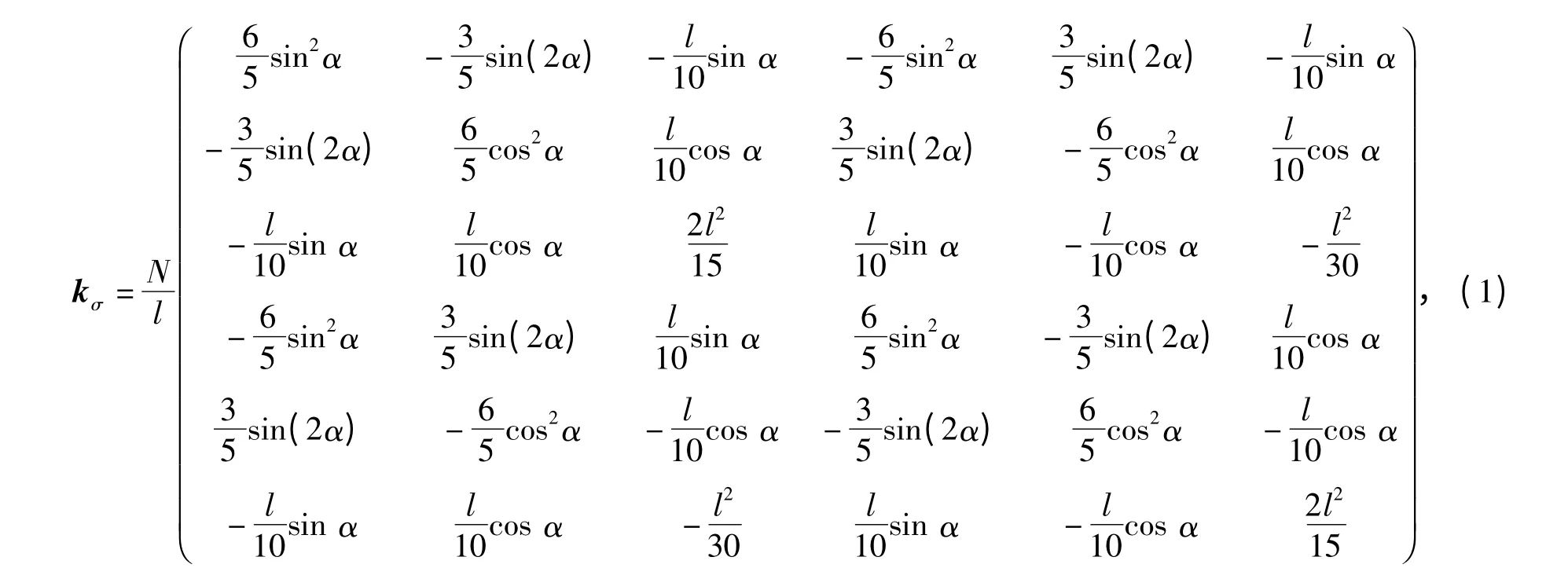
式中:α 为整体坐标系的Ox 轴与局部坐标系的O'x'轴的夹角，逆时针为正.

由能量法原理可以证明［10］，这一过程中单元几何形态改变引起的单元等效结点荷载向量

其中，

式中:A 为截面面积;I 为截面惯性矩;E 为单元材料的弹性模量;Feε 为单元中由几何变形引起的等效结点荷载向量;Feσ为单元中由应力引起的等效结点荷载向量.

式(3)和式(4)为一般形式，对斜拉索而言，将无应力曲率效应置0 即可. 此时，全过程控制条件下结构的几何非线性平衡方程为［10］:

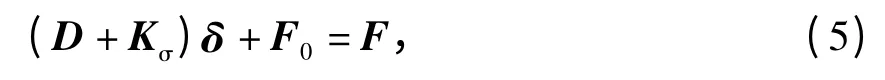
式中:D 为结构的弹性刚度矩阵(参见文献［10］，限于篇幅，不再赘述);Kσ为结构的几何刚度矩阵;δ 为杆系结构的结点位移向量;F0为结构的等效结点荷载向量;F 为结构所受的外荷载向量.

不考虑无应力长度和无应力曲率等几何状态效应时，式(5)退化为传统的几何非线性平衡方程.式(5)表明，可将单元几何形态改变引起的效应等效为结点荷载的形式，建立最终状态与结构形成过程各状态之间的数值关系，从而实现从构件制造到结构最终完成整个过程中各施工阶段的分析计算，为全过程控制的实施奠定理论和分析方法基础.

2.2 误差效应传播方程

在已知构件理论无应力几何形态的条件下，可由式(5)确定施工全过程各关键施工阶段的结构状态.下面根据式(5)推导误差效应的传播方程.由于主梁、索塔节段和斜拉索的制造误差一般均较小，可以忽略制造误差引起的外荷载向量F 的变化.为不失一般性，假定单元无应力长度的制造误差和两端无应力曲率的制造误差分别为Δl0、Δki0和Δkj0，则单元实际制造形态的几何要素为:

将l'取代式(1)中的l，可得此时的单元几何刚度矩阵kσ'(加“'”表示计入误差后的参数)，进而得Kσ'，同理可得D';将l'、ki0'和kj0'分别取代式(3)～(4)中的l0、ki0和kj0，可以确定单元实际制造形态引起的等效结点荷载向量'，据此可得此时的等效结点荷载向量F0'. 此时，结构的几何非线性平衡方程变为

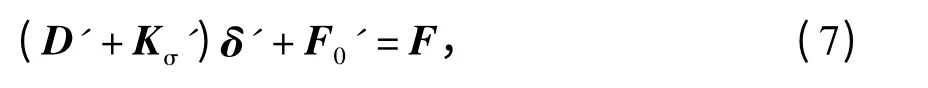
式中，δ'为计入制造误差后的结构结点位移.

由式(5)和式(7)可得:

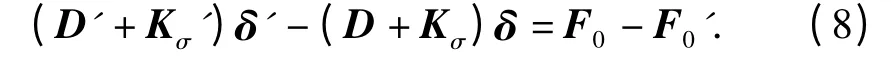
正常情况下，单元制造误差较小，可忽略制造误差对D 和Kσ的影响，则式(8)进一步简化为

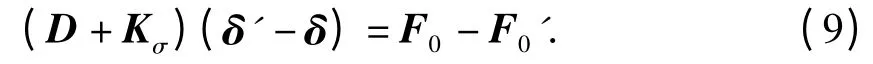
式(8)和式(9)即为误差效应传播方程. 可基于该方程实现构件制造误差效应特性的分析和求解，并进一步确定后续关键施工阶段制造误差效应的传播特性.因关键构件安装误差的效应特性与制造误差类似，故可将构件安装误差视为广义的构件制造误差，上述误差传播方程同样适用于构件安装误差效应的理论分析.所建立的误差效应传播方程应用和求解方便，适用于全过程控制条件下大跨度钢箱梁斜拉桥误差效应的理论研究和计算分析.

3 构件制造误差的效应特性

3.1 研究对象

苏通大桥主桥主跨1 088 m，是首座跨度超过1 000 m 的超大跨度钢箱梁斜拉桥.其主梁采用梁高4.0 m 的正交异性板流线型扁平钢箱梁，节段标准长度16 m，边跨尾索区标准长度12 m，全桥钢箱梁共分为141 个梁段.斜拉索采用空间双索面扇形布置，每个索面布置34 对，全桥共272 根. 索塔采用倒Y 形结构，索塔高300.4 m.

在苏通大桥施工控制过程中，各梁段和斜拉索的编号规则(该桥有南通侧和苏州侧2 座塔，对各塔的梁段和斜拉索分别编号，因梁段和斜拉索对称布置，编号方式相同，故对此未加区分):岸侧和江侧分别用A 和J 表示，数字随梁段距索塔中心距离的增大而增大，如江侧最靠近跨中的斜拉索编号为J34#，中跨最大悬臂主梁节段编号为J34#，其余类似.为便于后续各图表示，将主跨跨中作为顺桥向纵坐标的坐标原点，苏州侧方向为正.

苏通大桥主梁节段和斜拉索施工过程主要包括3 个阶段:(1)梁段匹配拼装工况，该工况为控制工况，主要控制对象为待安装梁段和已安装梁段之间的无应力角度;(2)对应梁段的斜拉索一张工况，该工况为非控制工况;(3)对应斜拉索的二张工况，该工况为控制工况，主要控制对象为待安装斜拉索的无应力长度.以J21#梁段和斜拉索拼装施工为例，其控制工况的典型施工过程见图2(T0-20中，T0为初始张拉索力，20 表示编号为20#的斜拉索;其余类似).

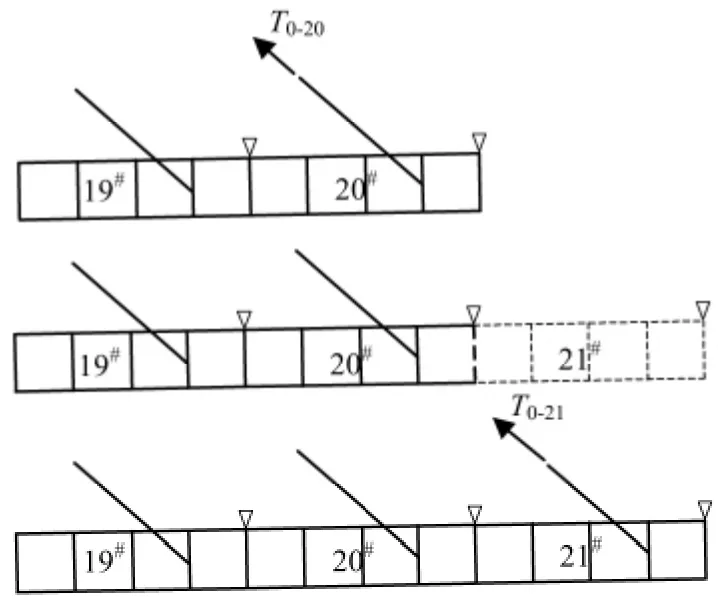
图2 典型施工过程示意Fig.2 Typical construction procedure of girders and cables

3.2 误差效应的形成和传播过程

误差效应传播方程表明:全过程控制条件下，构件制造误差引起的与其无应力长度和无应力曲率相关的等效荷载向量改变，是导致结构状态误差的根本原因.由全过程控制的实现方式和施工过程可知:成桥理想目标状态的主梁线形、内力和斜拉索索力等控制目标是通过确保关键构件几何形态的相互关系实现的.构件制造误差的存在直接导致上述各关键构件间几何形态的关系偏离理想值，具体表现为关键施工阶段的结构状态误差. 因此，在结构出现状态误差的情况下，可以通过修正后续安装关键构件间的几何形态关系实现误差调控.这就是全过程控制条件下结构状态误差控制的理论依据.

现以苏通大桥典型施工工况——J20#梁段拼装为例，扼要阐述状态误差的形成及传播过程. 为便于说明，假定:(1)J20#梁段的制造长度比其理想制造长度长10.0 mm，即该梁段的无应力长度误差Δl= +10.0 mm;(2)该梁段及后续梁段均按照梁段间的理论几何形态关系进行制造和拼装控制;(3)各斜拉索均按照其理论无应力索长进行安装控制.J20#梁段制造长度误差导致的典型施工阶段的状态误差和成桥阶段的状态误差分别见图3 和图4.

结果表明:(1)J20#梁段无应力制造长度误差直接导致该梁段及其相邻梁段出现线形和索力状态误差，J20#梁段线形及其对应斜拉索的索力误差显著高于其他梁段;(2)各梁段前端点的线形误差随其与J20#梁段距离的增大而逐步减小并趋于稳定值，一直持续到成桥阶段;(3)J20#梁段无应力长度误差导致的成桥阶段线形和索力误差的最大值均出现在该梁段及其对应斜拉索;(4)在不采取有效的误差效应调控措施的条件下，将无法有效控制梁段无应力长度误差导致的线形和斜拉索索力误差.上述状态误差的形成和传播过程见图5.

图3 典型施工过程的状态误差Fig.3 Typical errors in typical construction procedures

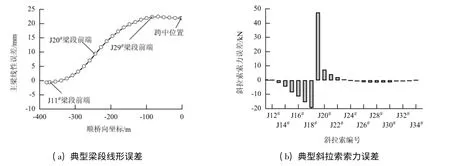
图4 成桥阶段状态误差Fig.4 Typical errors after completion

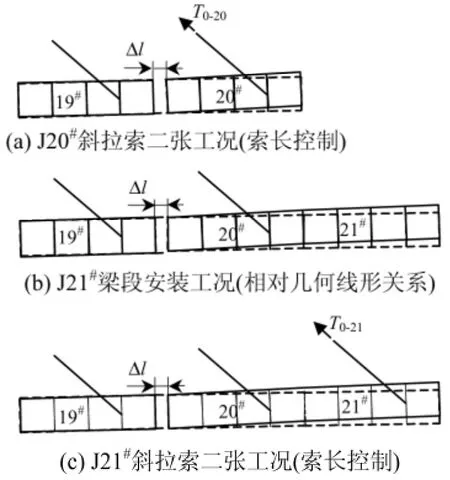
图5 施工过程状态误差的形成和传播过程Fig.5 Generation and propagation of construction errors

全过程控制条件下，根据斜拉索上下索锚点(分别位于索塔和主梁)的坐标及其安装阶段斜拉索的索力确定无应力长度，并据此进行斜拉索的安装控制.斜拉索二张工况为苏通大桥斜拉索的张拉控制工况. 在J20#梁段无应力制造长度误差为+10.0 mm 的情况下，J20#斜拉索下索锚点的纵坐标出现相应的误差，按理论无应力索长对该斜拉索进行张拉控制时，其索力大于理论值，并进而直接导致两类状态误差.

(1)斜拉索索力误差.梁段长度制造误差导致的各梁段质量的误差极小，即J20#斜拉索及其附近区域斜拉索的竖向分力总和保持不变，J20#斜拉索的索力误差使得该区域斜拉索的索力重分配，导致此前已安装的多根斜拉索索力小于理论值，出现负误差，而其后安装的多根斜拉索索力则出现正误差.索力误差的影响范围主要限于J20#斜拉索附近区域，主梁越纤柔，该影响区域越小. (2)线形误差.J20#斜拉索的索力误差导致J19#和J20#梁段主梁的线形高于理论线形，发生正误差. 根据J21#和J20#梁段间的夹角进行J21#和后续梁段拼装控制时，各梁段的线形相应地发生正误差，斜拉索下锚点的纵坐标和竖向坐标均发生改变，进而导致各斜拉索的无应力长度误差——斜拉索索力误差产生的主要原因.

上述误差效应的产生和传播过程表明:(1)关键构件的无应力几何形态误差是导致全过程控制条件下关键施工阶段结构状态误差的根本原因;(2)构件无应力几何形态误差导致的状态误差具有自身的形成和传播特性，主梁线形和斜拉索索力两类典型的状态误差具有耦合性，二者同时发生，且相互影响，共同组成斜拉桥的主要状态误差.

3.3 制造误差的效应特性

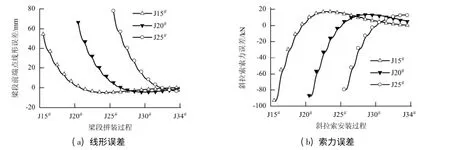
图6 主梁节段无应力角度误差效应的传播特性Fig.6 Condition error propagation induced by fabrication angle errors of girder segments

全过程控制条件下，大跨度钢箱梁斜拉桥主梁和索塔索锚点位置的制造误差导致斜拉索的安装误差，其误差效应与斜拉索制造误差的效应一致.以主梁无应力长度误差、梁段间的无应力角度误差和斜拉索长度制造误差3 类典型制造误差为研究对象，对制造误差的效应特性进行了系统、深入研究，限于篇幅，仅给出典型结果.为便于说明，主要考虑发生系统制造误差的情况，不涉及随机误差和多种制造误差的耦合效应问题.以施工控制中最重要的2 类状态误差指标——主梁线形误差和斜拉索索力误差为例探讨制造误差的效应特性.

根据梁段间无应力角度制造和控制的实现方式，通过主梁节段顶底板的制造误差间接定义角度误差，即在梁段底板或顶板制造长度保持不变的情况下，其顶板或底板制造长度误差等效于主梁节段间的无应力角度误差.各主梁节段底板的制造误差均为+1 mm 时引起的主梁线形和斜拉索索力误差效应见图6.

主梁节段和斜拉索无应力制造长度误差均分别为+2 和-2 mm 导致的主梁线形和斜拉索索力误差效应分别见图7 和图8.

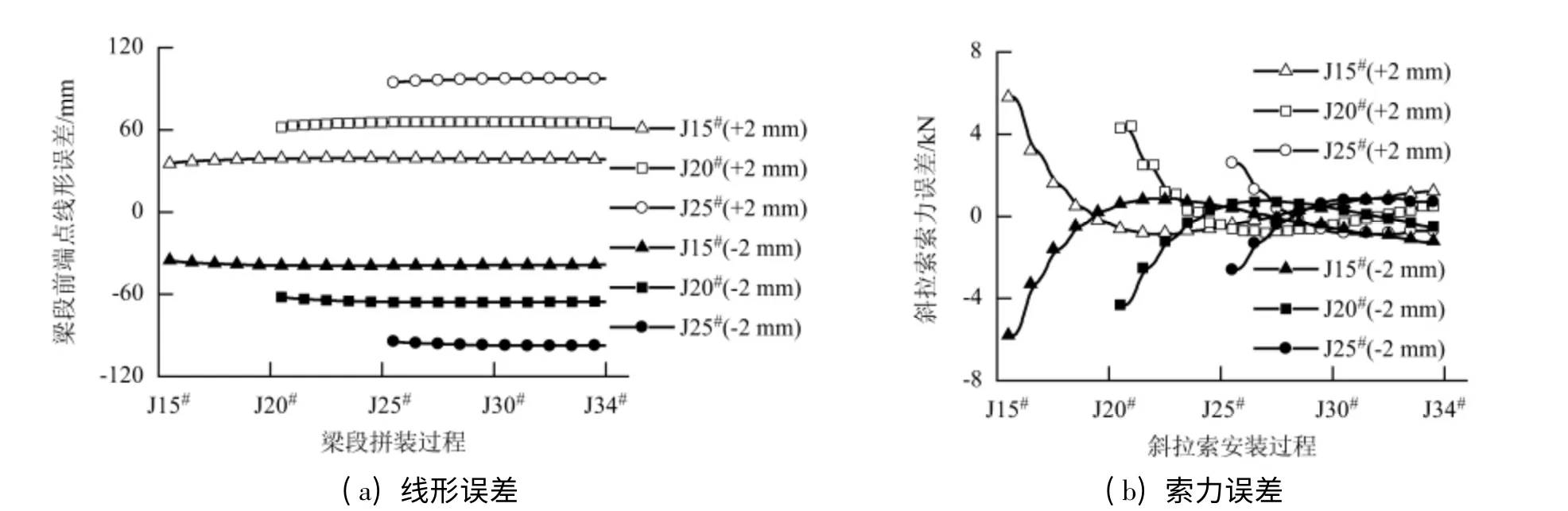
图7 主梁节段长度制造误差效应的传播特性Fig.7 Condition error propagation induced by fabrication length errors of girder segments

研究表明，不同类型构件制造误差的效应及传播特性具有显著差异:(1)主梁节段的无应力角度误差导致的主梁线形和斜拉索索力误差均具有典型的自收敛性，即其误差效应随悬臂长度增大逐步减小，这一过程实质上是无应力角度的误差效应随结构刚度减小逐步减弱的过程.(2)主梁节段长度制造误差效应在主梁线形和斜拉索索力两类状态误差上表现出截然不同的特性，各典型梁段的线形误差效应基本不随悬臂长度增大而增大，梁段距跨中越近，其线形误差效应越显著，且误差效应量值较大，不容忽视;大悬臂条件下各斜拉索索力误差较小，且随悬臂长度增大而迅速降低. (3)斜拉索制造长度的误差效应主要表现为主梁线形误差.

因主梁自重不变，超大跨度斜拉桥主梁相对纤柔，且各斜拉索自身制造长度误差的影响不像主梁梁段一样具有延续性，因此，较小的斜拉索制造长度误差导致的斜拉索索力误差也较小.

图8 斜拉索长度制造误差效应的传播特性Fig.8 Condition error propagation induced by fabrication length error of cables

各主梁节段无应力角度误差和长度制造误差导致的主梁线形误差效应包络图见图9.因误差效应相对于主跨跨中具有对称性，仅给出其中一侧主跨线形误差的计算结果.

图9 主梁线形误差效应包络图Fig.9 Envelope diagram of girder shape error induced by fabrication errors

研究表明:(1)主梁底板制造误差均为-1 mm时，随悬臂长度增大，主梁线形状态误差为负值，即实际线形低于理论线形，新增梁段安装工况线形误差的绝对值保持不断增大的趋势.主梁底板制造误差均为+1 mm 时，在误差量值与上面的情况相反，但误差效应随悬臂长度增大的变化趋势一致.(2)对主梁节段间无应力角度制造误差效应取绝对值，其最大值的曲线斜率随悬臂长度增大不断减小，即实际误差状态效应表现出一定程度的自收敛性.(3)主梁节段长度制造误差的效应特性与主梁节段间无应力角度制造误差的效应特性存在显著差别:该误差导致的主梁线形误差和曲线斜率随悬臂长度增大而不断增大，主梁线形误差效应表现出典型的发散特性;误差包络图上下限值基本相同，同一类型的主梁节段制造长度误差导致的误差效应量值基本保持不变，波动性较小. (4)两类误差的实际效应均不容忽视，只有通过适当的误差调控措施才能抑制其不良效应.(5)相对于主梁节段间无应力角度制造误差而言，主梁节段长度制造误差的效应更显著，主要表现为误差效应量值绝对值较大且不具备自收敛性.

4 结 论

由几何非线性平衡条件推导并建立了全过程控制条件下的误差效应传播方程，探讨了苏通大桥关键构件制造误差效应的形成机理及其在施工全过程中的传播特性，得到以下结论:

(1)所建立的全过程控制条件下的误差效应传播方程适用于大跨度钢箱梁斜拉桥全过程施工控制误差效应研究和计算分析，研究结果可为误差调控决策提供科学依据.

(2)由构件制造误差引起的与其无应力长度和无应力曲率相关的等效荷载向量改变，是导致结构状态误差的根本原因.

(3)不同类型制造误差的误差效应和传播特性存在显著差异:随悬臂长度增大，主梁节段间制造角度的误差效应表现出典型的自收敛特性;主梁节段制造长度误差导致的主梁线形误差在悬臂施工过程中基本保持不变，不具备自收敛特性;斜拉索制造长度误差则主要导致主梁线形误差.

必须指出，施工控制实施时，应根据不同制造误差的效应特性进行科学、合理地误差调控决策.原始误差、测量误差和环境误差综合影响下的大跨度斜拉桥误差特性及其调控是下一阶段研究的重点.

［1］ VIRLOGEUX M. Recent evolution of cable-stayed bridges［J］. Engineering Structure，1999，21:737-755.

［2］ 郝超. 大跨度钢斜拉桥的施工监控及其目标精度［J］. 中国公路学报，2003，16(1):54-57.HAO Chao. Construction control and control precision goal of long-span steel cable-stayed bridge［J］. China Journal of Highway and Transport，2003，16(1):54-57.

［3］ 葛耀君. 分阶段施工桥梁分析与控制［M］. 北京:人民交通出版社，2003:134-155.

［4］ MANABE Y，HIRAHARA N，MUKASA N，et al.Accuracy control on the construction of the Tatara bridge［C］∥IABSE Conference. Malmö，Sweden:［s.n.］，1999:322-331.

［5］ 李乔，唐亮. 悬臂拼装桥梁制造与安装线形的确定［C］∥第十六届全国桥梁学术会议论文集:上册.北京:人民交通出版社，2004:297-302.

［6］ 卜一之，赵雷，李乔. 苏通长江大桥结构非线性稳定性研究［J］. 土木工程学报，2013，46(1):84-91.BU Yizhi，ZHAO Lei，LI Qiao. Structural nonlinear stability analysis of Sutong Yangtze River bridge［J］.China Civil Engineering Journal，2013，46(1):84-91.

［7］ 秦顺全. 桥梁施工控制:无应力状态法理论与实践［M］. 北京:人民交通出版社，2007:96-108.

［8］ 李乔，卜一之，张清华. 基于几何控制的全过程自适应施工控制系统研究［J］. 土木工程学报，2009，42(7):69-77.LI Qiao，BU Yizhi，ZHANG Qianhua. Whole-procedure adaptive construction control system based on geometry control method［J］. China Civil Engineering Journal，2009，42(7):69-77.

［9］ 李乔，卜一之，张清华. 大跨度斜拉桥施工全过程几何控制概论与应用［M］. 成都:西南交通大学出版社，2009:140-173.

［10］ 黄灿. 基于几何控制法的大跨度斜拉桥自适应施工控制体系研究［D］. 成都:西南交通大学土木工程学院，2011.

［11］ LI Qiao，BU Yizhi，ZHANG Qinghua. Adaptive geometrical construction control method of super longspan cable-stayed bridges［C］∥18th IABSE Congress.Seoul:［s.n.］，2012:101-109.

［12］ 黄灿，赵雷，张清华. 特大跨度斜拉桥制造阶段参数敏感性分析及工程应用［J］. 四川建筑科学研究，2011，37(3):297-300.HUANG Can， ZHAO Lei， ZHANG Qinghua.Sensitivity analysis of parameters of the manufacturing stage for super-span cable-stayed bridge and its application［J］. Sichuan Building Science，2011，37(3):297-300.

［13］ 颜东煌，陈常松，董道福，等. 大跨度钢主梁斜拉桥的自适应无应力构形控制［J］. 中国公路学报，2012，25(1):55-58.YAN Donghuang，CHEN Changsong，DONG Daofu，et al. Control of self-adaptive zero-stress configuration for long-span cable-stayed bridge with steel main girder［J］. China Journal of Highway and Transport，2012，25(1):55-58.

［14］ 张清华，卜一之，李乔. 大跨度斜拉桥施工控制的研究进展［C］∥第二十届全国桥梁学术会议论文集:上册. 北京:人民交通出版社，2012:521-529.

［15］ 贾少敏，赵雷，卜一之. 分幅不对称索面钢箱梁斜拉桥主梁安装控制［J］. 桥梁建设，2014，44(3):114-119.JIA Shaomin，ZHAO Lei，BU Yizhi. Erection control of main girder of steel box girder cable-stayed bridge with separated decks and asymmetric cable planes［J］.Bridge Construction，2014，44(3):114-119.