循环流化床提升管压力瞬时波动研究

刘宝勇，魏绪玲，张 斌

（1.兰州交通大学化学与生物工程学院，甘肃 兰州 730070；2.中国石油石油化工研究院兰州化工研究中心，甘肃 兰州730060）

化学工程

循环流化床提升管压力瞬时波动研究

刘宝勇1，魏绪玲2，张 斌1

（1.兰州交通大学化学与生物工程学院，甘肃 兰州 730070；2.中国石油石油化工研究院兰州化工研究中心，甘肃 兰州730060）

在φ0.4m×9.1m 循环流化床提升管中采集了分布板以上不同轴向高度的气体压力瞬时波动信号，并利用统计方法和功率谱进行分析。结果表明，在相同操作气速条件下，固体颗粒循环速率越大，在同一轴向位置，压力平均值越大；在相同操作条件下，压力标准偏差随轴向高度的增加而减小；功率谱谱图中存在一个明显主频。

循环流化床；压力；瞬时波动；统计分析

循环流化床（Circulating Fluidized bed，简称CFB）在炼油、化工、能源、冶金、材料和环保等领域有着广泛应用，例如炼油工业中的FCC、化学工业中的丙烯氨氧化合成丙烯腈、能源工业中的CFBB和煤化工中的Fischer-Tropsch合成[1]等。

提升管压力瞬时波动信号及其规律是研究固体颗粒-流化气体两相流动特性的一种有效手段[2]。压力瞬时波动中包含着提升管内气-固两相流动特性的大量信息，综合反映了其整体流化特性，是流化颗粒特性、流化床结构特性及所产生气泡特性的耦合反映[3-4]，且具有混沌特性[5-6]。研究压力瞬时波动规律有助于深入掌握提升管内流动状况、流型转变[7]、故障检测和动力学性质[8]等。

1 实验装置与方法

1.1 物料特性

流化固体颗粒采用石英砂（无内孔，属Geldart B类），采用液体置换法测定的颗粒真实密度为2690kg·m-3。由Rise 2002型激光粒度分析仪测得平均粒径为108 μm，粒径分布如图1所示。

1.2 实验装置

实验装置如图2所示。该装置主要由提升管和2个鼓泡流化床构成。提升管内径0.4m，高度9.1m。鼓泡流化床2种固体颗粒处于鼓泡流化状态，其主要作用是为提升管3稳定供料。固体颗粒在提升管3内实现快速流化，气体夹带固体颗粒进入旋风分离器4，在此分离得到的固体颗粒经鼓泡流化床5返回鼓泡流化床2，实现循环流化。罗茨风机提供常温空气作为过程流化气体，提升管内气体流量由角接取压标准孔板流量计（LCBH-01型）测量，2个鼓泡流化床内气体流量由转子流量计（LHB型）测量。提升管固体颗粒进料量由连接提升管3和鼓泡流化床2的管线上的蝶阀开度调节。固体颗粒循环速率通过切换法得到，具体做法为:在单位时间内取循环物料，称重，并经换算得到，取料位置位于旋风分离器4底部。

图1 流化颗粒的粒径分布

1.3 实验方法[9]

提升管压力瞬时信号由差压变送器（型号FD80CCIIERC3Lm）测量。实验过程中由数据采集板（型号SF-630，采集频率为100Hz）将差压变送器获得的电流信号转化为电压信号，再利用微型计算机转化为压力瞬时波动信号，显示并记录保存。

图2 实验装置示意图

在不同操作条件下，采集提升管分布板以上各轴向高度的一定时间段内的压力瞬时波动数据，本实验过程中采样时间设定为60 s。所测压力瞬时波动数据经校正后得到最终实验数据。

2 实验结果与讨论

2.1 压力瞬时波动

不同操作条件下，提升管分布板以上轴向高度H=0.11 m处，具体压力瞬时波动信号如图3所示。

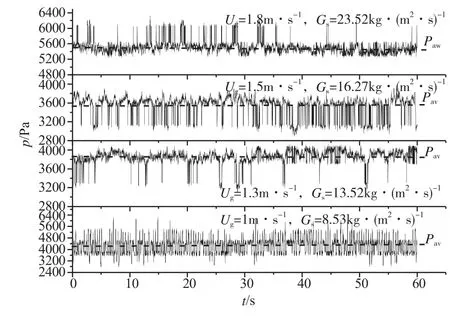
图3 不同操作条件下压力瞬时波动（H=0.11 m）

在同一轴向位置，不同操作条件下的压力瞬时波动的表观特征不同，在不同时间点，压力可能偏离平均值，或上或下，幅度和趋势亦不同。H=0.11m处，Ug=1m·s-1，Gs=8.53kg·(m2·s)-1时，压力上下波动相对均匀，但偏离程度较大；平均值Pav=4236 Pa，伴随标准偏差σ=552.8 Pa。Ug=1.3 m·s-1，Gs=13.52 kg·(m2·s)-1时，若压力高于平均值，波动较小，最大值Pmax= 4086 Pa；若压力低于平均值，波动较大，最小值Pmin=3096 Pa；总体上Pav=3854 Pa，伴随σ=148.9 Pa。Ug=1.5 m·s-1，Gs=16.27 kg·(m2·s)-1条件下，若压力高于平均值，波动较小，Pmax= 3911 Pa；若压力低于平均值，波动较大，Pmin=2891 Pa；总体上Pav=3541 Pa，伴随σ=219 Pa。Ug=1.8 m·s-1，Gs=23.52 kg·(m2·s)-1条件下，若压力高于平均值，波动较大，Pmax= 6325Pa；若压力低于平均值，波动较小，Pmin=5267 Pa；总体上Pav=5509 Pa，伴随σ=165 Pa。不同操作条件下，压力瞬时波动规律不同，这也说明提升管底部区域具有不同的气-固两相流动状态。

造成压力瞬时波动的原因主要包括3个方面:一是流化过程会产生气泡，气泡行为导致波动，二是提升管床体振动，三是床层表面、底部分布板及布气室等位置压力波动的传播[2]。其中气泡行为(包括气泡形成、发展、聚并及破碎)是影响提升管内压力瞬时波动的主要因素[9]。提升管内是复杂多相体系，包括气-固相互作用、气泡行为、固体颗粒聚集体行为、装置床体振动和外来波动传播等多个方面，它们发生相互作用和耦合作用，导致压力瞬时波动情况非常复杂。为了从现有数据中得到尽可能多的有用信息，需要利用各种已有数学工具进行深入分析。常用方法包括统计分析和功率谱分析等。

2.2 压力瞬时波动的统计分析

通过统计分析方法可以获得压力瞬时波动的一些性质，如压力平均值、标准偏差及概率密度函数等，且简单快速。其中平均值为:

标准偏差为:

通过标准偏差可以衡量压力瞬时数据偏离平均值的程度，标准偏差数值越大，说明偏离程度越大。

不同操作条件下的压力瞬时波动平均值和标准偏差均随分布板以上轴向高度增加而变化，如图4所示。

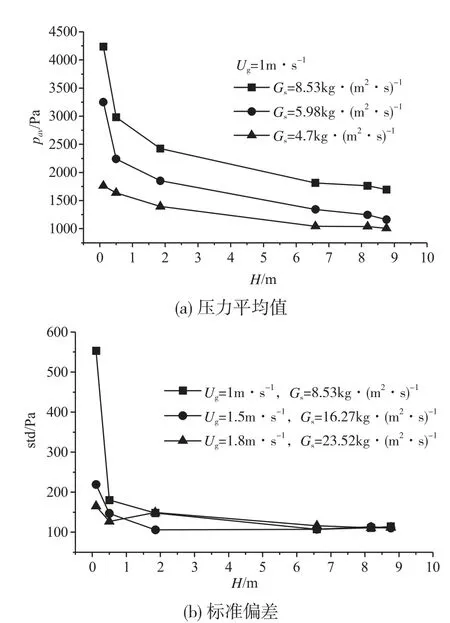
图4 压力平均值与标准偏差在轴向的分布

在相同操作气速下，固体颗粒循环速率越大，在同一轴向位置，压力平均值越大。原因是固体颗粒循环速率越大，提升管内固体颗粒数量越多，动力系统需要为颗粒加速及输送提供更多能量。压力平均值的轴向分布与固体颗粒平均浓度分布[11-12]是一致的。底部密相区固体颗粒浓度大，颗粒加速及输送需要消耗更多能量[13]，因此单位高度压力差值大。上部稀相区的固体颗粒浓度小，颗粒输送比底部密相区能耗少，单位高度压力差值小。Ug=1m·s-1，Gs=8.53 kg·(m2·s)-1时，H=0.11 m处，压力瞬时波动的标准偏差最大，σ=553 Pa；H=0.50 m处σ=180 Pa，减小很多，继续增加轴向高度，标准偏差继续减小，且随高度变化不大，在110 Pa左右，标准偏差减小说明了压力瞬时波动对平均值偏离程度减小。提升管中压力瞬时波动主要是气泡行为引起的，气泡在分布板风帽处产生，上升并发生聚并，由小变大，在密相区上表面破裂，会产生较大压力瞬时波动；压力瞬时波动在向提升管上部传播过程中会逐渐衰减，因此波动程度变小。Ug=1.5 m·s-1，Gs=16.27 kg·(m2·s)-1条件下，标准偏差分布趋势亦是如此。而Ug=1.8 m·s-1，Gs=23.52 kg·(m2·s)-1条件下，标准偏差数值普遍较小，总体上随轴向高度增加而减小，说明此时气-固两相流化状态为密相气力输送。

由图4(b)可知，上部稀相区在不同操作条件下的标准偏差差别不大，约为110 Pa，这说明分布板影响仅局限于底部密相区，在上部稀相区，固体颗粒浓度小，气-固两相接触充分，流动形态受操作条件影响不大，因此，压力瞬时波动情况变化不大，主要受稀相区气-固两相流动特性控制。

2.3 压力瞬时波动的功率谱分析

功率谱分析是化学工程试验数据的常用分析手段之一。通常，通过自相关函数来描述某一时刻数据与另一时刻数据之间的相互依赖关系，计算式为:

将自相关函数进行傅立叶变换就得到功率谱密度函数，即:

功率谱密度函数是一种频域函数，蕴含着数据频率域方面的信息。通过功率谱分析可以获得能量在频率域的分布，在谱图中振幅大小随频率先增后减，存在着一个明显的振幅最大点，这一点的能量最大，习惯上称该点对应频率为主频[10]。可以通过多种方法来估计功率谱，具体可分为参数化方法和非参数方法两种。通过比较，本文采用的方法是Multitaper方法，属于非参数方法。相互独立的谱估计主要运用正交窗口来获取，之后再组合成最终谱估计[11]。

压力瞬时波动信号功率谱分析表明，谱图中存在着一个明显的主峰，即振幅最大点，对应频率即为主频fp。随频率增高，超过主频fp后，振幅A数值逐渐衰减。压力瞬时波动的功率谱如图5所示。在H=0.11 m处， Ug= 1m·s-1，Gs=8.53 kg·(m2·s)-1条件下，压力瞬时波动信号的功率谱为图5(a)，振幅峰值54.3 dB，对应fp=2.45 Hz。Ug=1.5 m·s-1，Gs=4.75kg·(m2·s)-1条件下压力瞬时波动信号的功率谱为图5(b)，振幅峰值30.95 dB，对应fp=3.7 Hz。从图5各图中均能发现，压力瞬时波动的低频部分振幅大，意味着能量高；高频部分振幅小，意味着能量低，可见低频部分是引起压力瞬时波动的主要原因。

3 结论

由于压力瞬时波动信号的复杂性，本文采用了多种分析手段对其进行了分析:

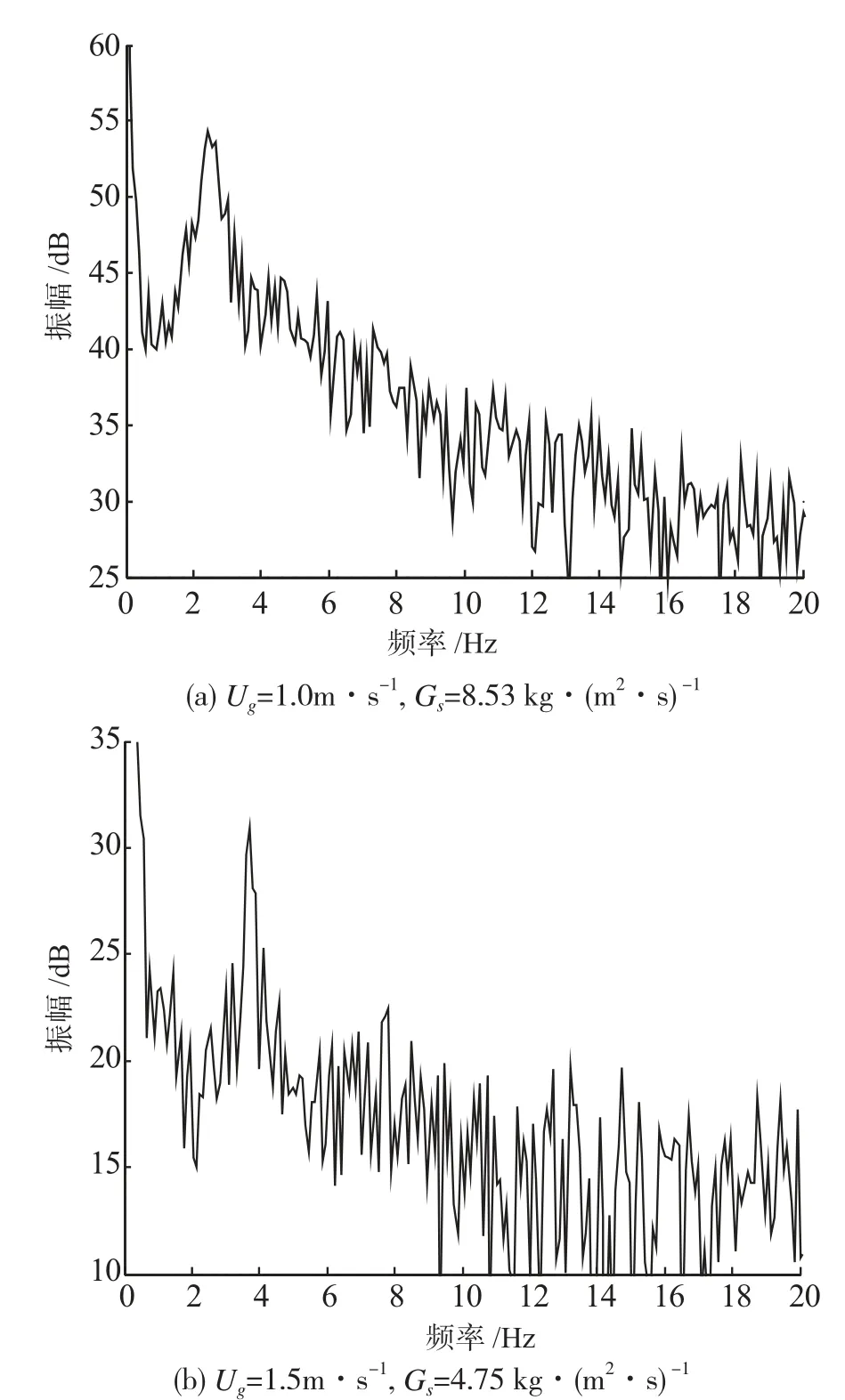
图5 压力瞬时波动的功率谱（H=0.11 m）

1) 平均值和标准偏差分析表明，在相同操作气速下，固体颗粒循环速率越大，在分布板以上同一轴向位置，压力平均值越大；相同操作条件下，标准偏差随轴向高度的增加而减小。

2) 通过分析压力瞬时信号的功率谱发现，不同谱图中均存在一个明显的主频。

[1] 刘宝勇，魏绪玲，郭庆杰，等.大型循环流化床底部区域颗粒浓度波动研究[J]. 兰州交通大学学报， 2009，28(3):174-179.

[2] Bi H T. A critical review of the complex pressure fluctuation phenomenon in gas-solids fluidized beds[J]. Chemical Engineering Science, 2007, 62(13): 3473-3493.

[3] 马丽萍，石炎福，黄卫星，等.循环流化床颗粒浓度波动信号多重分形测度分析[J]. 高校化学工程学报，2002，5(12):496-502.

[4] 黄海，黄轶伦，张卫东.气-固流化床压力脉动信号的相关结构模型与分析[J]. 化工学报，1999，50(6):812-817.

[5] 赵贵兵，陈纪忠，阳永荣.流化床压力波动混沌性质探讨[J].化工学报，2002，53(6):654-658.

[6] Marzocchella A, Zijerveld R C, Schouten J C, et al. Chaotic Behavior of Gas-Solid Flow in the Riser of a Laboratoryscale Circulating Fluidized Bed [J]. AIChE Journal, 1997, 43(6): 1458-1468.

[7] 周章玉，石炎福，余华瑞.由压力波动判断气-固流化床中的流化类型[J].化学反应工程与工艺，1999，15(3):262-267.

[8] 王其成，张锴，任金天，等. Geldart B类颗粒气-固流化床内的压力波动特性[J]. 燃料化学学报，2009，37 (6): 763-768.

[9] 刘宝勇.大型循环流化床底部区域气固两相流动特性研究[D].东营:中国石油大学（华东），2008.

[10] 黄海，黄轶伦，张卫东.气-固流化床压力脉动信号的Hilbert-Huang谱分析[J].化工学报，2004，55(9): 1441-1447.

[11] 金涌，祝京旭，汪展文，等.流态化工程原理[M].北京:清华大学出版社，2001:126-145.

[12] Yang W C. Handbook of fluidization and fluid-particle systems[M].New York: Marcel Dekker, 2003: 485-491.

[13] 黄卫星，石炎福，祝京旭.上行气-固两相流充分发展段的颗粒浓度[J].化工学报，2001，52(1):963-968.

[14] 郭庆杰，王启民，徐猛，等.高温鼓泡流化床的压力波动[J].燃烧科学与技术，2002，8(6):487-492.

[15] 陈亚勇. MATLAB信号处理详解[M].北京:人民邮电出版社，2001.

Research on Pressure Instantaneous Fluctuations in Riser of Circulating Fluidized Bed

LIU Bao-yong1, WEI Xu-ling2, ZHANG Bin1
(1. School of Chemical and Biological Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China；2. Lanzhou Petrochemical Research Center, Petrochemical Research Institute, PetroChina, Lanzhou 730060, China)

The experiments were carried out in a circulating fluidized bed of 0.4m in diameter and 9.1m in height to determine pressure instantaneous fluctuations at riser wall of different axial levels up the distribution plate. And the data measured were systematically analyzed using statistical methods and power spectrum. It was found that at the same operating gas velocity and axial location, average pressure increased with increasing solid circulation rate. And at the same operation condition, standard deviations in the axial direction decreased with increasing height in the axial direction. Furthermore, it was found that there was an obvious principal frequency in power spectrum.

circulating f uidized bed; pressure; instantaneous f uctuation; statistics analysis

TQ 021.1

A

1670-9905(2015)05-0058-04

甘肃省自然科学基金项目（1310RJZA066）；兰州交通大学青年科学基金项目（2013011）

刘宝勇（1981-），男，博士在读，讲师，主要从事化学工程和材料学的教学与研究工作，电话13893138207，E-mail: liuby@mail.lzjtu.cn

2015-03-04