拓扑优化技术在桥梁截面优化设计中的应用研究
2015-01-11常诚
常 诚
(山西省交通科学研究院,山西 太原 030006)
0 引言
近年来,我国的公路建设高速发展,兴建了大量的桥梁工程,在设计过程中,桥梁各构件的截面(如主梁截面、桥墩截面、斜拉桥的塔柱截面等)优化设计尤为重要,基于此,本文提出了拓扑优化技术在截面优化中的应用。
根据研究对象的不同,拓扑优化可以分为离散拓扑优化与连续体拓扑优化。1964年,Dron等人提出了基结构法,将数值方法引入结构设计领域,该方法将实际结构离散为杆件连接而成的基结构,通过优化算法将多余的杆件从结构中剔除,从而获取最优构形。Rozvany等人建立了桁架结构拓扑优化的最优准则,根据这一准则,可以在完备的设计域中确定最优解。
谢忆民和Steven于1992年提出了渐进结构优化算法(ESO),此方法可以解决静态、动态结构的尺寸、形状和拓扑优化问题。该方法基本概念简单,而且具有较好的通用性,可借助当前通用的有限元分析软件作为分析平台。荣见华等人[1-2]提出了基于灵敏度的渐进结构优化算法和基于人工材料的拓扑优化设计方法。刘毅[5]提出了基于固定网格的双向渐进结构优化方法,将双向固定网格渐进结构优化方法应用于符合材料板壳开孔形状优化。
渐进结构优化算法的另一特点是双向进化[3]。传统的渐进结构优化算法主要依靠删除单元来获取优化构形。但是由于在某些迭代过程中,一些单元会被过度删除,之后无法恢复,因此其准确性受到影响,从而限制了此方法的应用。基于应力准则的双向优化算法,其原理是在高应力单元周围增加单元,在低应力区删除低应力单元,使得单元杀死和单元生成同时进行,提高了算法的适应性。
1 拓扑优化算法
本文实现的拓扑优化技术基于渐进结构优化算法(ESO)。其基本原理为:不断地从连续体中剔除传力效率不高的单元,最后生成结构的主要荷载传递构架。优化的目标是:以最少的材料、最合理的拓扑形状,来实现结构总体刚度的最大化,即结构应变能密度的最小化[4]。优化的目标函数为:

式中:Ci为结构中第i个单元的应变能;Wi为第i个单元的重量。
定义结构的性能指标[5]为:

C0、W0、Ci、Wi分别表示初始状态下及经过第 i次优化后结构的总应变能和总重量。
对平面应力状态下的各向同性材料,可采用Mises应力准则[6]:

式中:σVM是单元的 Mises应力;σ1、σ2、σ3分别代表第一主应力、第二主应力与第三主应力。
首先求出每点的应力值,假设第j个单元的单元应力为σj,结构中某此迭代的最大单元应力为,则如果
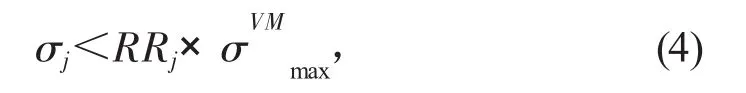
则认为该单元应力偏小,利用单元杀死技术将该单元刚度设置为一个极小值,其中RRj为单元删除率。
通过迭代求解,当式(4)无法满足时,即已达到稳定状态。为使有效迭代继续进行,引入一个进化参数ER,进化公式为:
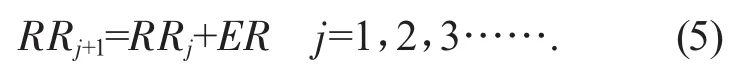
2 算例
2.1 算例1
某混凝土简支梁,长70 cm,高30 cm,底部承受如图1所示的集中力,F=50 kN。材料弹性模量E=3.25×1010Pa,密度 ρ=2 300 kg/m3,泊松比 λ=0.3。有限单元类型为Plane42,单元尺寸esize=0.5 cm,共划分5 600个四边形单元。
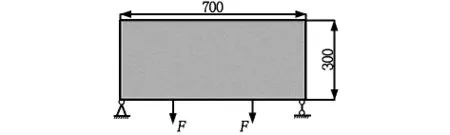
图1 简支梁示意图(单位:mm)

图2 第22次迭代

图3 第45次迭代

图4 第109次迭代
图2~图4分别为结构在第22、45、109次的迭代求解结果,其中图4为最优拓扑构形。从图中可以看出,迭代初期,单元的删除从远离荷载一侧的两个端角点开始,并在结构中部两集中荷载之间形成矩形孔洞。迭代进行到第45步时,两集中力上方分别优化出3根“杆”,矩形孔洞进一步增大;在第109次迭代时,3根杆件进化为2根,拱结构进一步细化,结构优化指标PI达到最大值。
2.2 算例2
某混凝土悬臂梁,长50 cm,高20 cm,端部承受如图5所示的集中力,F=30 kN。材料弹性模量E=3.25×1010Pa,密度 ρ=2 300 kg/m3,泊松比 λ=0.3。有限单元类型为Plane42,单元尺寸esize=0.5 cm,共划分4 000个四边形单元。
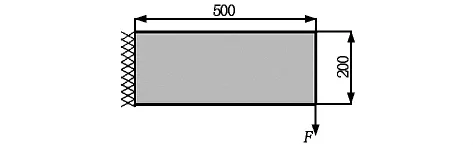
图5 悬臂梁示意图(单位:mm)

图6 第80次迭代

图7 第128次迭代

图8 第168次迭代
图6~图8分别为结构在第80、128、168次的迭代求解结果,其中图8为最优拓扑构形。从图中可以看出最优构形为“半拱形”结构。其中“拱腹杆”位置与拉、压应力迹线的走向类似。

图9 结构优化指标PI
根据式(2)可知,指标PI越大,说明拓扑构形越合理,材料利用率越高。简支梁与悬臂梁算例的PI的变化趋势如图9所示。从图中可以看出两者的指标分别在第109次迭代与第168次迭代中达到最大,这与两算例分别在第109次迭代与第168次迭代中获取最优构形是相符的。
3 结论
基于渐进结构优化算法的思想,本文实现了连续体结构的拓扑优化技术。该技术主要依靠低效率单元的删除策略来获取最优拓扑构形。该技术依托通用有限元软件ANSYS,通过编制APDL程序来实现。数值算例表明,该算法具有较好的计算稳定性。本文算法同样适用于三维问题以及同时考虑应力和位移约束的问题,对桥梁各构件的截面优化设计具有实际工程意义。
