由一个概率问题引发的思考

由一个概率问题引发的思考

廖明芳

(咸宁市教育科学研究院，湖北 咸宁 437100)

概率问题在日常生活中有很多的应用，但在解决问题的过程中，往往存在一些争议，例如对题目中某些文字的理解是否正确？和日常生活的惯性思维是否存在反差？以及对事件的准确区分导致错误的概率公式选择,都会影响到题目最后正确的解答。中学数学教学参考2009年第4期(上旬)P19 《是P(AB)还是P(B|A)》，就谈及了此类条件概率的问题。初中九年级教材中也有一个概率题，联想到湖北高考的一道概率题我有如下思考：

试题1：(9年级数学教科书下册 人教版P163)动物学家通过大量的调查估计出，某种动物活到20岁的概率为0.8，活到25岁的概率为0.5，活到30岁的概率是0.3，现年20岁的这种动物活到25岁的概率为多少？现年25岁的这种动物活到30岁的概率是多少[1]？

教参答案：(题目的含义为：从出生活到20岁的概率为0.8；从出生活到25岁的概率为0.5；从出生活到30岁的概率为0.3。此题需要学生对用频率估计概率有更深层次的理解)

试题2：(2005年湖北高考21题)某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同，假定每盏灯能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p1。寿命为2年以上的概率为p2。从使用之日起每满1年进行一次灯泡更换工作，只更换已坏的灯泡，平时不换。

(Ⅰ)在第一次灯泡更换工作中，求不需要更换灯泡的概率和更换两只灯泡的概率；

(Ⅲ)当p1=0.8，p2=0.3时，求在第二次灯泡更换工作中，至少需要更换4只灯泡的概率(结果保留两位有效数字)。

(Ⅱ)对该盏灯来说，在第1、2次都更换了灯泡的概率为(1-p1)2；在第一次未更换灯泡而在第二次需要更换灯泡的概率为p1(1-p2)，故所求的概率为p=(1-p1)2+p1(1-p2)。

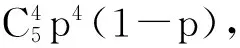
第二种答案是：

解：因为该型号的灯泡寿命为1年以上的概率为p1，寿命为2年以上的概率为p2。

所以寿命为1～2年的概率应为p1-p2。其分布列为：

第一种浪形划分是针对2449点上升的正常回调。2703点运行的是ABC三浪下跌调整结构，C3已经结束于2489点或者是已经结束于2462点了，目前处于C4小微浪的反弹过程当中；最关键的问题是这里的C5小微浪并不能确认最后会运行到哪里。因为C5小微浪可以是失败的不创新低的，甚至C3-5小浪和C5小浪有时候都很难进行有效的区分清楚。

寿命0～11～22～p1-p1p1-p2p2

(Ⅱ)在第二次灯泡更换工作中，对其中的某一盏灯来说，该盏灯需要更换灯泡是两个独立的事件：

(1)在第1、2次都更换了灯泡的概率为(1-p1)2;

(2)在第一次未更换灯泡而在第二次需要更换灯泡的概率为p1-p2,故所求的概率为p=(1-p1)2+(p1-p2)。

(Ⅲ)由(Ⅱ)当p1=0.8，p2=0.3时，在第二次灯泡更换工作中，对其中的某一盏灯来说，该盏灯需要更换灯泡的概率p3=(1-p1)2+(p1-p2)=0.54。

在第二次灯泡更换工作，至少换4只灯泡包括换5只和换4只两种情况:

故至少换4只灯泡的概率为：p4=0.046+

0.196=0.242。

即满两年至少需要换4只灯泡的概率为

0.242。

试题2两种解法的不同集中体现在第(2)问中的第二种情况，即第一次未更换而第二次更换灯泡的这个事件概率上。之所以出现这种差异，主要是对题意中的文字理解有误，灯泡使用寿命1年以上，就是以1年为界限，一年内概率(1-p1)，1年后概率p1，同样灯泡使用寿命2年以上，就是以2年为界限，两年内概率(1-p2)，2年后概率p2，所有事件均以新灯泡起计算，以某一个时间为界，不存在解法二中的1年到2年之间的这样一个事件，所以p1-p2的解答我认为是有误的。这个问题在此不多做赘述。

对于以上两道概率题，出现在不同学段的概率问题上，可谓解答方法完全不同，考察的知识点也大相径庭，对学生知识层面的要求更是不同,但对于此两个问题，我认真研读了多遍，试图寻找二者之间的牵连与异同。

2005年湖北高考的这道题当时引发了很多的争议，由于对文字理解的不同，导致出现两种答案，而九年级的教材上此问题的再现，让我再次惊叹，这两道题的背景是何其的相似，解法却完全不同(不管是高考题中的哪种解法)，为何会出现如此大的差别，让我们一起来追踪两道题的来龙去脉：

记A={灯泡寿命1年以上}，B={灯泡寿命2年以上}；C={动物活到20岁}，D={动物活到25岁}，E={动物活到30岁}。动物活到20岁即已经到了20岁,也就是活到20岁以上。从题目隐含的意义上来讲,这两道题中给出事件所创设的情境是相同的,都指寿命年限的,那么每个事件所指的年限就应该是从出生到这个时间截止,活到了这个时间期限，事件A和事件B所代表的含义不妨用下面的图示观察:

试题1图示:

试题2图示:

从图示上我们可以清晰的发现,B⊂A，E⊂D⊂C，

故而P(AB)=P(B)，P(CD)=P(D)，P(DE)=P(E)

我们用分析概率题的一般思想来看问题,首先我们应该看到事情的本质属性，这里的事件A、B属于概率中的相容事件。所以高中教材中涉及的相互独立事件、互斥事件都不适合此题。

对以上两道题的分析可以看出，概率的考察无处不在，初中考察频率估计概率，从数字分数的角度看问题，而高中从几类基本事件的分析，概率的公式上做计算，到了大学，学习了全概率公式，贝叶斯公式，学生就会拉一条纵线，看到浑然一体的概率体系。

由此我们也可以发现,虽然解法不同,但所反映的概率知识是一致的,均符合大学概率论与数理统计中的理论,出现在不同学段,教法解法不同是可以理解的。使得学生在学习知识的过程中有较强的连续性,即看待问题的角度不同而已。为此我们提倡大学的有关概率知识的下放,到高中,更要到初中,这样层层深入的学习,有利于学生形成一个逐步加深的稳固知识体系,从知识上生长出新知识的学习方式更牢固，能够从不同层面的看问题,能够更清楚的了解知识的所以然,能够形成自己的分析问题的思维方式，大有裨益。

[1]人民教育出版社，课程教材研究所.数学(九年级下册)[M].北京：人民教育出版社，2008.163.

2095-4654(2015)10-0198-02

2015-08-12