纳米层状结构非局域等离激元传播长度研究

李军，肖玉婷，徐国定，潘涛

（苏州科技学院数理学院，江苏苏州215009）

纳米层状结构非局域等离激元传播长度研究

李军，肖玉婷，徐国定，潘涛*

（苏州科技学院数理学院，江苏苏州215009）

研究了非局域效应情况下，表面等离子体激元在以各向异性材料为衬底的纳米层状结构中的传播特性。详细推导了表面等离子体激元在各向异性纳米层状结构中的色散关系式，并通过数值计算，研究了对称与反对称两种不同模式下传播长度随结构和材料等参数的变化关系。

各向异性;非局域;传播长度

随着纳米制造技术的发展，微型化、高密度化、高速化将会成为集成光学的发展趋势。衍射极限的限制成为集成光学发展过程中存在的根本性困难。近年来，人们发现金属与电介质界面上存在的一种被称为“表面等离子体”的电磁模式，其横向的尺寸小于波长，可以实现对电磁场亚波长的束缚，从根本上突破了衍射极限的限制[1-2]。表面等离子体的特性使其被广泛的运用到了各个领域，例如，全光存储[3]、纳米光学成像[4]、生物光学[5]。研究表面等离子体激元在复合结构中的传播特性，并且通过改变材料结构和材料参数来获得更好的传播特性成为国内外学者研究的热点。

当器件结构的尺寸不断地减小到几百纳米甚至几纳米时，非局域效应会在电磁波传播过程中起到至关重要的作用。非局域效应也成为国内外学者研究纳米结构波导时不得不考虑的一个因素[6-12]。R.Ruppin详细介绍了非局域效应对表面等离子体激元在层状结构中传播的影响[6]。黄杨等研究了在考虑非局域情况下表面等离子体激元对于金属纳米线结构的传播特性[7]。

为了获得更好的传播特性，许多新材料被引入到纳米波导结构中。各向异性材料由于能够有效地影响电磁场传播的边界条件，被学者广泛地应用到各种波导结构中。Jacob，et al把各向异性材料引入到IMI和MIM两种不同的结构中，并研究了表面等离子体激元在两种不同结构中的传播特性[13]。近年来，表面等离子体激元的传播长度问题已引起众多学者的关注。陈建军等研究了四层结构中表面等离子体激元的传播长度[14]，Nagaraj，et al利用各向异性材料改变了表面等离子激元在层状结构中的传播长度[15]，Krokhin，et al以一种强各向异性的材料为衬底，从而获得长程表面等离子体激元[16]。

1 基础理论

1.1 理论推导

笔者研究的纳米结构模型是一个典型的三明治结构，在以下的分析中采用了笛卡尔坐标系。中间层（0＜z＜d）为极薄的金属层（金层）；衬底（z＜d）为半无限大的单轴三方各向异性材料，其介电常量为[εr]=diag(εx，εy，εz)，其中εx=εy；z＞d的部分为空气。其具体结构如图1所示。

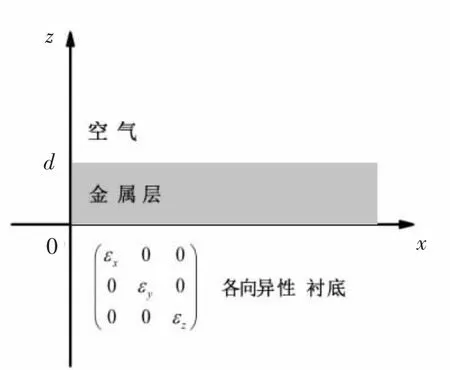
图1 各向异性材料为衬底的纳米层状结构

表面等离子体激元沿着x轴传播，其磁场平行于y轴。在各向异性衬底层中，利用麦克斯韦方程组，其电场和磁场可以表示成如下形式

1.2 非局域效应

当金属层的厚度小到几十纳米甚至几纳米时，非局域效应将会变得至关重要且不能忽略，基于经典的自由电子气体理论Drude模型已不再适用，一个更加详细、精确的流体动力学模型被提出。

其中，β为非局域参数。由于电位移矢量D满足▽·D=0，因此，自由电子极化矢量Pf可以表示成

摘 要：教师在数学教学活动的开展过程中，有效地利用数字化的学习资源，能够促使学生发现数学学科的魅力，开展有效的教学活动，同时能够促使学生在接受知识的过程中，培养自身的分析、思考、发现问题的能力，丰富自身的数学知识系统，进行数学知识的吸收理解。教师利用数字化的学习资源能够打破传统教学理念的束缚，真正地进行素质教育，从而达到预期的教学效果。

其中，χb是束缚电子的磁化系数。

考虑非局域效应情况下，麦克斯韦方程组表示如下[10]

方程组（5）和（6）的解有两种情况：第一种解满足▽·E=0，即普通形式的麦克斯韦方程组，相对应的波称为横波，其电场的表达式为

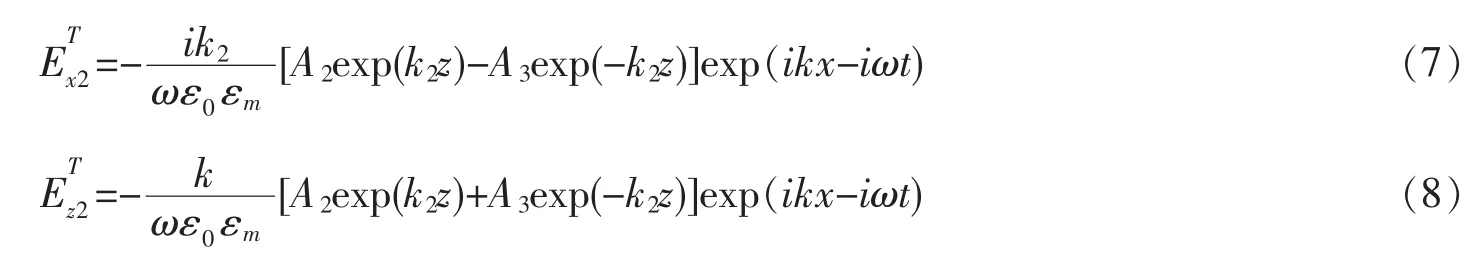
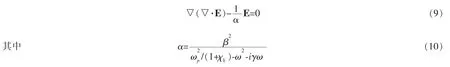
由（9）式可以得到纵波的电场表达式

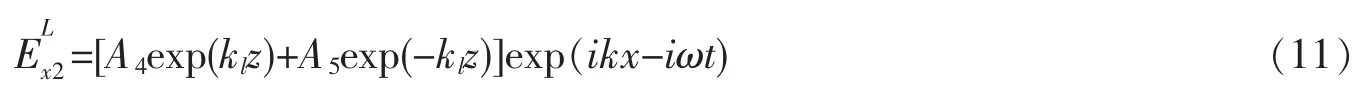
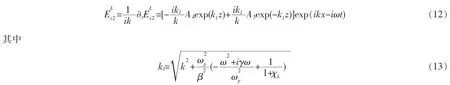
由于纵波没有相对应的磁场，因此，金属层中磁场的表达式为

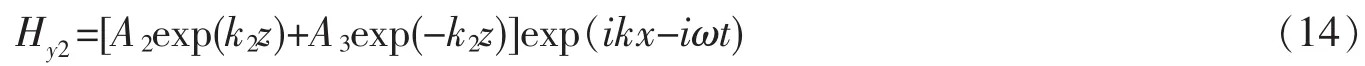
金属层中总电场为横波和纵波的电场之和，其表达式如下

1.3 边界条件

非局域效应导致一种新的纵波的产生，原有的边界条件已经无法来确定唯一的场方程。因此，一个额外的边界条件被提出：由于自由电子无法逃离金属层，在金属和介质层的界面处，其电荷密度应为零。这个合理的额外的边界条件表示如下[8，10]

再根据原有的边界条件，在z=0和z=d处，Hy，Ex是连续的。可以得到一个色散关系的矩阵表达式

2 数值计算

接下来，通过数值计算方法，进一步研究等离子体激元在层状纳米结构中的传播长度，以及受相关物理量的影响。相关参数如下：对于金属层（金层）的非局域参数，其中费米速度νF=1.36×106m·s-1，阻尼参数γ=0.075 2 eV，相位频率ωp=8.812 eV[11]；对于各向异性材料，首先取εx=7.5，εz=2；由于在非局域效应中起主要作用的是自由电子，因此,令束缚电子的磁化系数χb=0。

首先由式（18），获得在考虑非局域效应情况下，表面等离子体激元在层状纳米结构中的色散关系曲线，如图2所示。从图2可以看出表面等离子体激元在层状纳米结构中的色散关系有上下两支曲线，通过与局域色散关系的比较[6，12-13]，得上支表示对称模式，下支表示反对称模式。

笔者重点研究的是等离子体激元在层状纳米结构中的传播长度，其表达式如下

其中，k″=Im（k）。笔者分别讨论了两种不同模式下传播长度随着金属层厚度的变化特征，如图3所示。从图3可看出，在对称模式下，表面等离子体激元的传播长度随着金属层厚度的增加而减小，并很快趋于饱和；相反，在反对称模式下，表面等离子体激元的传播长度随着金属层厚度的增加而增加，这意味着随着金属层厚度的增加，电磁场进入金属层的深度不断增加。

图2 表面等离子体激元在各向异性纳米层状结构中的色散关系曲线

图3 表面等离子体激元在纳米层状结构中传播长度随金属层厚度的变化关系曲线

各向异性材料的性质对传播长度也有着明显的影响。图4表示了两种不同模式下传播长度随着各向异性参数εx/εz的变化关系曲线。由图4可看出，与各向同性（εx/εz=1）相比，当εx＜εz，两种模式的表面等离子体激元的传播长度随εx/εz减小（各向异性程度增大）而增大，并且对称模式下的传播长度总是大于相同条件下反对称模式的传播长度；而当εx＞εz时，两种模式的表面等离子体激元的传播长度随εx/εz增大（各向异性程度增大）而减小，并且当εx/εz大约大于1.82时，反对称模式的传播长度大于对称模式。

图4 表面等离子体激元在纳米层状结构中传播长度随各向异性材料参数的变化关系曲线

3 结语

利用流体动力学模型，推导了非局域情况下，表面等离子体激元在各向异性材料为衬底的纳米层状结构中的色散关系，并利用数值计算得到了色散关系曲线。通过色散关系，发现表面等离子体激元在非局域的纳米层状结构中有两种不同的传播模式，即对称模式和反对称模式。针对两种不同的模式，研究了传播长度和金属层厚度的关系，在反对称模式下，厚度对传播长度的影响比较大；而在对称模式下，厚度对传播长度的影响范围较小，并且无论金属层厚度是多少，反对称模式的传播长度总是大于对称模式。此外，衬底材料的各向异性对非局域情况下的表面等离子体激元影响更为敏感，无论是对称模式还是反对称模式都有较大的调制范围，这也提供了一种有效的控制表面等离子体激元的传播长度的手段。

[1]Zia R，Schuller J A，Chandran A，et al.Plasmonics：the next chip-scale technology[J].Material Today，2006，9（7-8）：20-27.

[2]Berini P.Long-range surface plasmon polaritons[J].Adv Opt Phot，2009，1（3）：484-588.

[3]Ditlbacher H，Lamprecht B，Leitner A.Spectrally coded optical data storage by metal nanoparticles[J].Opt Lett，2000，25（8）：563－565.

[4]Wang G P，Sugiura T，Kawata S.Holography with surface-plasmon-coupled waveguide modes[J].Appl Opt，2001，40（22）：3649－3653.

[5]Kabashin A V，Evans P，Pastkovsky S，et al.Plasmonic nanorod metamaterials for biosensing[J].Nat Mater，2009，8（11）：867－871.

[6]Ruppin R.Non-local optics of the near field lens[J].J Phys，2005，17（12）：1803－1810.

[7]Huang Y，Gao.Equivalent permittivity and permeability and multiple Fano resonances for nonlocal metallic nanowires[J].J Phys Chem C，2013，117（37）：19203－19211.

[8]Ciracì C，Pendry B，Smith R.Hydrodynamic model for plasmonics：a macroscopic approach to a microscopic problem[J].Chem Phys Chem，2013，14（6）：1109－1116.

[9]Scalora M，Vincenti M A，D de Ceglia，et al.Second-and third-harmonic generation in metal-based structures[J].Phys Rev A，2010，82（4）：043828－043841.

[10]Moreau A，Ciracì C，Smith D R.Impact of nonlocal response on metallodielectric multilayers and optical patch antennas[J].Phys Rev B，2013，87（4）：045401－045412.

[11]Raza S，Toscano G，Jauho A P，et al.Unusual resonances in nanoplasmonic structures due to nonlocal response[J].Phys Rev B，2011，84（12）：121412－121417.

[12]Raza S，Christensen T，Wubs M，et al.Nonlocal response in thin-film waveguides：loss versus nonlocality and breaking of complementarity[J]. Phys Rev B，2013，88（11）：115401－115411.

[13]Jacob J，Babu A，Mathew G，et al.Propagation of surface plasmon polaritons in anisotropic MIM and IMI structures[J].Superlattices Microstruct，2008，44（3）：282－290.

[14]Chen J J，Li Z，Gong Q H.Long-rang surface plasmon polaritons with subwavelength mode expansion in an asymmetrical system[J].Chin Phys B，2009，18（8）：3535－3541.

[15]Nagaraj，Krokhin A A.Long-range surface plasmons in dielectric-metal-dielectric structure with highly anisotropic substrates[J].Phys Rev B，2010，81（8）：085426－085435.

[16]Krokhin A A，Neogi A，McNeil D.Long-rang propagation of surface plasmons in thin metallic film deposited on an anisotropic photonic crystal[J]. Phys Rev B，2007，75（23）：235420－235425.

Propagation length of surface plasmon polartions with nonlocal response in nanostructure

LI Jun，XIAO Yuting，XU Guoding，PAN Tao*
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

Taking into consideration the nonlocal effect，we investigated the propagation properties of surface plasmon polartions in anisotropic nanostructure.We derived the dispersion relation of surface plasmon polartions in anisotropic nanostructure.Based on the numerical calculation,the dependence of propagation length on the structure and material parameters in symmetric and antisymmetric modes was discussed in detail.

anisotropic；nonlocal effect；propagation length

O441.4

A

1672－0687（2015）01－0031－05

责任编辑：李文杰

2014－10－10

江苏省产学研前瞻性联合研究项目（BY2011133）

李军（1988-），女，江苏苏州人，硕士研究生，研究方向：复杂结构电磁波传播。

*通讯联系人：潘涛（1960-），男，教授，硕士生导师，E-mail:wlxpt@163.com。