2n-周期二元序列的5-错线性复杂度

周建钦，王洪翠

（1.杭州电子科技大学通信工程学院，浙江杭州310018；2.安徽工业大学计算机科学与技术学院，安徽马鞍山243032）

2n-周期二元序列的5-错线性复杂度

周建钦1，2，王洪翠1

（1.杭州电子科技大学通信工程学院，浙江杭州310018；2.安徽工业大学计算机科学与技术学院，安徽马鞍山243032）

密钥流序列的随机性检测和稳定性度量的两项重要指标：线性复杂度与k-错线性复杂度，对密钥流序列密码强度的研究具有极其重要的意义。分析讨论汉明重量最小的错误序列是计算给定k-错线性复杂度条件下所对应的原序列个数的一个有效方法。使用该方法，分别给出了5-错线性复杂度等于2n-3+x，2n-2-2n-m以及2n-1-2n-3时，周期和线性复杂度均等于2n的原序列s（n）的计数公式，并通过计算机编程进行了验证。

密钥流序列；线性复杂度；k-错线性复杂度；k-错线性复杂度分布

线性复杂度与k-错线性复杂度分别用来度量密钥流序列的随机性和稳定性。为了避免攻击者通过B-M算法[1]得到整个序列，密钥流序列的线性复杂度应该尽量大。1983年，国外学者Games和Chan提出了2n-周期二元序列线性复杂度的快速算法[2]。然而，现实的通信过程中是存在干扰的，当密钥流序列被改变少量比特时，其线性复杂度可能急剧下降。例如，24-周期二元序列s（4）=｛1000 0000 0000 0000｝，其线性复杂度为16，改变s（4）的一个比特，得到全零序列后，其线性复杂度降为0。我国学者丁存生，肖国镇和单炜娟[3]最早关注这个问题，随后国外学者Stamp与Martin[4]引入k-错线性复杂度的概念作为度量序列稳定性的一个指标。国内学者苏明通过对F2上2n-周期序列线性复杂度与1-错线性复杂度的研究，发现在一定条件下，不同序列具有固定的1-错线性复杂度[5]。随后，Meidl给出了线性复杂度为2n的2n-周期二元序列的k-错线性复杂度分布[6]，k=1，2。

为了计算给定k-错线性复杂度条件下原序列的个数，先求线性复杂度等于给定的k-错线性复杂度的二元序列p（n）的个数和汉明重量不大于k的可能成为错误序列的u（n）的个数。之后，基于组合数学的筛选法，排除不满足条件的序列u（n），从而给出5-错线性复杂度等于2n-3+x，2n-2-2n-m和2n-1-2n-3时，周期和线性复杂度均等于2n的原序列s（n）的计数公式。

1 预备知识

定义1[7]设在GF（q）上，N-周期序列s=（s0，s1，…，sN-1）N，其k-错线性复杂度LCk（s）定义为

其中，e=（e0，e1，…，eN-1）N，WH（e）表示序列e在一个周期内的汉明重量。

引理1[8]设周期为2n的二元序列，如果，则有；如果，则有。

引理2[9]设周期为2n的二元序列s（n），若s（n）的一个周期内的汉明重量为奇数，则LC（s（n））=2n；若s（n）的一个周期内的汉明重量为偶数，则LC（s（n））＜2n。

引理3[10]设Ei表示周期为2n的二元序列，且序列一个周期内只有第i位上的元素是1，其他元素全为0，0≤i＜2n。如果j-i=2r（1+2a），a≥0，0≤i＜j＜2n，r≥0则LC（Ei+Ej）=2n-2r。

引理4[11]设s（n）为2n-周期二元序列，其线性复杂度为L，N（L）表示满足以上条件的序列s（n）的个数，则

引理5i）设2n-周期二元序列p（n），LC（p（n））=c，1≤c＜2n-1-3，且c≠2n-1-2d1，2≤d1≤n-2，c≠2n-1-2d1-2d2，0≤d2＜d1≤n-2。若u（n）也是2n-周期序列，WH（u（n））=1，3或5，则LC5（p（n）+u（n））=c。

ii）设2n-周期二元序列p（n），LC（p（n））=c，c=2n-1-2d1，0≤d1≤n-2，或c=2n-1-2d1-2d2，0≤d2＜d1≤n-2。则存在序列u（n），WH（u（n））=1，3或5，使得LC5（p（n）+u（n））＜c。

证明求p（n）+u（n）的5-错线性复杂度，就是在p（n）+u（n）上叠加汉明重量为1，3或5的序列，然后求其最小线性复杂度。

i）设不同于u（n）的序列v（n），WH（v（n））=1，3或5。

若LC（u（n）+v（n））≥2n-1，则LC（p（n）+u（n）+v（n））≥2n-1。由LC（p（n）+u（n）+v（n））=c，1≤c＜2n-1-3，故LC5（p（n）+u（n））=c。

若LC（u（n）+v（n））＜2n-1，则有Left（u（n）+v（n））=Right（u（n）+v（n）），此时WH（Left（u（n）+v（n）））=2或4，LC（u（n）+v（n））=LC（Left（u（n）+v（n）））=2n-1-2d1，0≤d1≤n-2或2n-1-2d1-2d2，0≤d2＜d1≤n-2，因此，LC（p（n）+u（n）+v（n））= max［LC（p（n）），LC（u（n）+v（n））］。

综上，LC（p（n）+u（n）+v（n））≥LC（p（n）），故LC5（p（n）+u（n））=min［LC（p（n）+u（n）+v（n））］=c。

ii）设序列p（n），LC（p（n））=c，c=2n-1-2d1，0≤d1≤n-2，或c=2n-1-2d1-2d2，0≤d2＜d1≤n-2，则存在序列u（n），WH（u（n））=1，3或5和序列v（n），WH（v（n））=1，3或5，使得LC（u（n）+v（n））=c，即LC5（p（n）+u（n））＜c。

证毕。

2 5-错线性复杂度的原序列计数公式

引理6设s（n）为2n-周期二元序列，N5（2n-3+x）表示线性复杂度等于2n，5-错线性复杂度等于2n-3+x的序列s（n）的个数，n≥5，1≤x＜2n-4，则

证明设序列s（n）=p（n）+u（n），其中LC（p（n））=2n-3+x，1≤x＜2n-4，WH（u（n））=1，3或5，则u（n）有个。

下面分两种情况加以讨论，一种是LC5（p（n）+u（n））＜2n-3+x，另外一种是存在不同于p（n）的序列q（n），使得p（n）+u（n）=q（n）+v（n），此时有s（n）=p（n）+u（n）=q（n）+v（n），也就是说s（n）多加了一倍。

现假设w（n）=u（n）+v（n），WH（u（n））=1，3或5，WH（v（n））=1，3或5，并且LC（w（n））≤2n-3+x，1≤x＜2n-4。这样LC（w（n））≤2n-3+x＜2n-2，因此，WH（w（n））=8并且呈4等分分布，即有LC（w（n））=2n-2-2n-m，3≤m≤n。

当m=3时，有LC（w（n））=2n-3＜2n-3+x；当m＞3时，有LC（w（n））=2n-2-2n-m≥2n-2-2n-4=2n-3+2n-4＞2n-3+x。因此，m只能为3。

故LC（u（n）+v（n））只能取2n-3，这样LC5（p（n）+u（n））＜2n-3+x的情况就不存在，只需讨论p（n）+u（n）=q（n）+v（n）的情况即可，具体情况如下：

（1）当WH（u（n））=3时，有唯一的序列v（n），WH（v（n））=5，使得LC（u（n）+v（n））=2n-3，这样的u（n）有个。（2）当WH（u（n））=5，且5个非零比特均属于w（n）时，有唯一的序列v（n），WH（v（n））=3，使得LC（u（n）+v（n））=2n-3，这样的u（n）有个。（3）当WH（u（n））=5，且只有4个非零比特属于w（n）时，也只有唯一的序列v（n），WH（v（n））=5，使得LC（u（n）+v（n））=2n-3，这样的u（n）有个。

根据引理4，满足LC（p（n）=2n-3+x的序列p（n）的个数为：。

综上，满足LC5（s（n））=2n-3+x的非平衡二元序列s（n）的个数为

证毕。

例如：当n=5，x=1，LC5（s（n））=5时，N5（5）=3 244 544，与计算机编程验证结果一致。

引理7设s（n）为2n-周期二元序列，N5（2n-2-2n-m）表示线性复杂度等于2n，5-错线性复杂度等于2n-2-2n-m的序列s（n）的个数，n≥4，4≤m≤n，则

其中，B1，B2，B3，B4，B5，B6，B7定义见证明过程。

证明设序列s（n）=p（n）+u（n），其中LC（p（n））=2n-2-2n-m，n≥4，4≤m≤n，WH（u（n））=1，3或5，则u（n）的个数为：个。

（1）根据引理5可知，存在不同于u（n）的序列v（n），WH（v（n））=3或5，使得LC（u（n）+v（n））=2n-2-2n-m，即LC5（s（n））=LC5（p（n）+u（n））=min[LC（p（n）+u（n）+v（n））]＜2n-2-2n-m。

设序列w（n）=u（n）+v（n），满足LC（w（n））=2n-2-2n-m，WH（w（n））=8，则w（n）的每个周期可以等分成长度为2n-2的四部分，且每部分恰有2个非零比特，其距离为2n-m的奇数倍。这样的w（n）有个。其中每个w（n）均与另外的个w（n）有4个非零比特的交集。这样的4个非零比特组合构成了集合P1={ai，ai+2n-2，ai+2n-1，ai+3·2n-2|0≤i＜2n-2}，易知集合P1的元素个数为2n-2。

①当WH（u（n））=3，WH（v（n））=5时，u（n）中的3个非零比特均属于w（n）中的8个非零比特。若这3个非零比特从属于P1中的组合，则这样的u（n）的个数为。若这3个非零比特不从属于P1中的组合，则这样的u（n）的个数为。因此，满足条件的u（n）总共有个。

②当WH（u（n））=5，WH（v（n））=3时，u（n）中的5个非零比特均属于w（n）中的8个非零比特，这样的u（n）有个。

③当WH（u（n））=5，WH（v（n））=5时，u（n）中的4个非零比特属于w（n）的8个非零比特。

（a）若这4个非零比特a1，a2，a3，a4属于集合P1，那么u（n）中的第5个非零比特a5与a1，a2，a3，a4的距离不能为2n-m的奇数倍，否则就与②中的情况重复，即u（n）中的5个非零比特均属于w（n）的8个非零比特。距a1，a2，a3，a4为2n-m奇数倍的位置有个，再减去a1，a2，a3，a4本身的4个位置，即a5只能位于剩下的2n-2m-1-4个位置。这样的u（n）有个。

（b）若这4个非零比特a1，a2，a3，a4不属于集合P1，这样的u（n）有个。然而，当4个非零比特中的a1，a2，a3从属于P1中的组合，a4，a5与a1，a2，a3间的距离为2n-m的奇数倍且a4，a5不从属于P1中的组合时，可从两个不同的w（n）中分离得到相同的u（n），即得到的u（n）是双倍的。a4，a5的位置有种选择，即这样的u（n）的个数为。

例如：由计算机编程可得，当w（n）为{1100 0000 1100 0000 1100 0000 1100 0000}时，u（n）可以为{1101 0000 1000 0000 1000 0000 0000 0000}；当w（n）为{1001 0000 10010000 10010000 1001 0000}时，u（n）同样可以为{1101 0000 1000 0000 1000 0000 0000 0000}。

因此，当WH（u（n））=5，WH（v（n））=5时，满足条件的u（n）有个。

（2）假设LC（w（n））=LC（u（n）+v（n））=2n-2-2n-k＜2n-2-2n-m，3≤k≤m-1，此时存在序列q（n）=p（n）+u（n）+v（n），使得LC（q（n））=LC（p（n）+u（n）+v（n））=2n-2-2n-m，即存在s（n）=q（n）+v（n）=p（n）+u（n），这样的w（n）总共有2n+k-6个。所有这样的序列w（n）构成集合P2，则集合P2的元素个数为2n+k-6。

④当WH（u（n））=3，WH（v（n））=5，并且u（n）中的3个非零比特均属于P2中的w（n）而不从属于P1中的组合时，这样的u（n）有个。此时，存在一个不同于u（n）的v（n），使得LC（u（n）+v（n））＜2n-2-2n-m。

⑤当WH（u（n））=5，WH（v（n））=3时，u（n）中的5个非零比特均属于P2中的w（n），并且当4个非零比特a1，a2，a3，a4属于集合P1，a5与a1，a2，a3，a4相距2n-k的奇数倍，即为2n-m的偶数倍时，u（n）与（a）的情况是重复的。这里u（n）对应的v（n）即为情况④,所以u（n）的个数为B5=B4，此时存在一个不同于u（n）的v（n），使得LC（u（n）+v（n））＜2n-2-2n-m。

⑥当WH（u（n））=5，WH（v（n））=5时，u（n））中的4个非零比特属于P2中的w（n）且不属于集合P1，否则会与②、（a）中的情况重复，这样的u（n）有个。

（c）假设u（n）中的3个非零比特a1，a2，a3从属于P1中的组合。

i）当a4与a1，a2，a3相距2n-k的奇数倍，a5与a1，a2，a3相距2n-m的奇数倍时，这里的u（n）与（b）中的u（n）是重复的，这样的u（n）有个。

ii）当a4与a1，a2，a3相距2n-k的奇数倍，a5与a1，a2，a3相距2n-j（k＜j＜m）的奇数倍时，有两个不同的v（n），使得LC（u（n）+v（n））＜2n-2-2n-m；同样，当a4，a5与a1，a2，a3相距均为2n-k（4≤k＜m）的奇数倍且a4，a5不从属于P1中的组合时，也有两个不同的v（n），使得LC（u（n）+v（n））＜2n-2-2n-m，这些情况要特殊考虑，这样的u（n）有个。而此时可从两个不同的w（n）中分离得到相同的u（n），即要减去双倍的u（n）的个数。

因此，满足以上条件的u（n）总共有个。此时，存在一个不同于u（n）的v（n），使得LC（u（n）+v（n））＜2n-2-2n-m。

（d）现在，来考虑（c）中的特殊情况ii）。当a4，a5与a1，a2，a3相距均为2n-k（4≤k＜m）的奇数倍且a4，a5不从属于P1中的组合时，存在不同于u（n）的序列v1（n），v2（n），v1（n）≠v2（n）且wH（v1（n））=wH（v2（n））=5，使得LC（u（n）+v1（n））=LC（u（n）+v2（n））=2n-2-2n-k＜2n-2-2n-m。当a4与a1，a2，a3相距2n-k的奇数倍，a5与a1，a2，a3相距2n-j（k＜j＜m）的奇数倍时，也存在不同于u（n）的序列v1（n），v2（n），v1（n）≠v2（n）且wH（v1（n））=wH（v2（n））=5，使得LC（u（n）+v1（n））=2n-2-2n-k＜2n-2-2n-m，LC（u（n）+v2（n））=2n-2-2n-j＜2n-2-2n-m。此时有q1（n）=p（n）+u（n）+v1（n），q2（n）=p（n）+u（n）+v2（n），LC（q1（n））=LC（q2（n））=2n-2-2n-m，即存在s（n）=p（n）+u（n）=q1（n）+v1（n）=q2（n）+v2（n）。此时的s（n）多加了两倍，因此，要减去u（n），v1（n），v2（n）总数的2/3。

下面考虑一种特殊情况。设n=6，m=6，则k可取3，4，5，将从属于P1中组合的3个非零比特a1，a2，a3视为基准点。设a4，a5与基准点相距均为2n-5=2的奇数倍且a4，a5不从属于P1中组合的u（n）构成集合Q1；a4与基准点相距2n-5=2的奇数倍，a5与基准点相距2n-3=8的u（n）构成集合Q2；a4与基准点相距2n-5=2的奇数倍，a5与基准点相距2n-4=4的奇数倍的u（n）构成集合Q3。

i）对于Q1中的u（n），当a4距基准点的距离为d1，a5距基准点的距离为d2时，存在不同于u（n）的序列v1′（n），v2′（n），使得s（n）=p（n）+u（n）=q1′（n）+v1′（n）=q2′（n）+v2′（n）。若d1，d2差值为4的奇数倍，则在v1′（n），v2′（n）中，a4′距新的基准点的距离均为4的奇数倍，a5′距新的基准点的距离均为2的奇数倍，即v1′（n）∈Q3，v2′（n）∈Q3。

若d1，d2差值为8，则在v1′（n），v2′（n）中，a4′距新的基准点的距离均为8，a5′距新的基准点的距离均为2的奇数倍，即v1′（n）∈Q2，v2′（n）∈Q2。

ii）对于Q2中的u（n），存在不同于u（n）的序列v1″（n），v2″（n），使得s（n）=p（n）+u（n）=q1″（n）+v1″（n）=q2″（n）+v2″（n）。在v1″（n）中，a4″，a5″距新的基准点的距离均为2的奇数倍；在v2″（n）中，a4″距新的基准点的距离为2的奇数倍，a5″距新的基准点的距离为8，此时v1″（n）∈Q1，v2″（n）∈Q2。

iii）对于Q3中的u（n），存在不同于u（n）的序列v1‴（n），v2‴（n），使得s（n）=p（n）+u（n）=q1‴（n）+v1‴（n）=q2‴（n）+v2‴（n）。在v1‴（n）中，a4‴，a5‴距新的基准点的距离均为2的奇数倍；在v2‴（n）中，a4‴距新的基准点的距离为2的奇数倍，a5‴距新的基准点的距离为4的奇数倍，此时v1‴（n）∈Q1，v2‴（n）∈Q3。

综上可得，v1′（n），v2′（n），v1″（n），v2″（n），v1‴（n），v2‴（n）均包含在集合Q1，Q2，Q3中。一般性的情况均可类似证明。

满足（c）中的特殊情况ii）的u（n）个数为。

根据引理4，满足LC（p（n））=2n-2-2n-m的序列p（n）总共有个。

综上所述，满足LC5（s（n））=2n-2-2n-m的非平衡周期二元序列s（n）的个数为

证毕。

例如：当n=5，m=5，LC5（s（n））=7时，N5（7）=11 184 128，与计算机编程检验结果一致。

引理8设s（n）为2n-周期二元序列，N5（2n-1-2n-3）表示线性复杂度等于2n，5-错线性复杂度等于2n-1-2n-3的序列s（n）的个数，n≥5，则

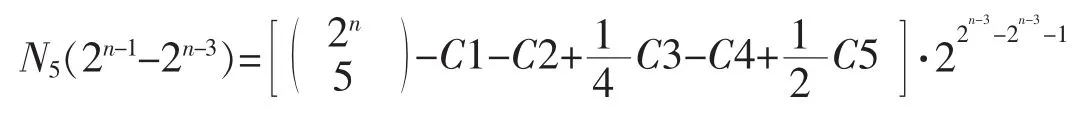
其中，C1，C2，C3，C4，C5定义见证明。

证明设s（n）=p（n）+u（n）序列，其中LC（p（n））=2n-1-2n-3，WH（u（n））=1，3或5，则u（n）有个。

（1）当WH（u（n））=1或3时，总存在序列v（n），WH（v（n））=3或5，使得LC（u（n）+v（n））=2n-1-2n-3，此时有LC5（s（n））= min[LC（p（n）+u（n）+v（n））]＜2n-1-2n-3。

（2）当WH（u（n））=5时，将u（n）分成2n-3个子序列，每个子序列中各个比特位置如下

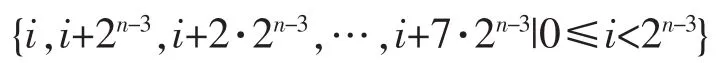
①当u（n）中至少有3个非零比特属于同一子序列时，肯定存在序列v（n），WH（v（n））=1，3或5，使LC（u（n）+v（n））=2n-1-2n-3，即LC5（s（n））=min[LC（p（n）+u（n）+v（n））]＜2n-1-2n-3。

当u（n）中的5个非零比特位于同一序列时，这样的u（n）有个；当4个非零比特位于同一子序列时，这样的u（n）有个；当3个非零比特a1，a2，a3位于同一子序列，另外两个非零比特a4，a5位于另外的一个子序列时，这样的u（n）有个；当a1，a2，a3位于同一子序列，而a4，a5另属于两个不同的子序列时，这样的u（n）有个。因此，有个u（n），使得LC5（s（n））=min[LC（p（n）+u（n）+v（n））]＜2n-1-2n-3。

②当u（n）中非零比特a1，a2位于同一子序列，a3，a4也位于同一子序列时，u（n）的个数为

当a1，a2与a3，a4这两对非零比特间的距离为2n-3的偶数倍时，这样的u（n）有个。其中，至少有一对非零比特的距离为2n-1的u（n）个数为，因此，

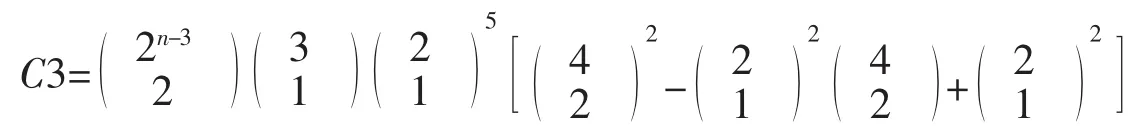
这时，存在3个不同于u（n）的v（n），WH（v（n））=5，使得LC（u（n）+v（n））＜2n-1-2n-3，即存在序列q（n）=p（n）+u（n）+v（n），LC（q（n））=2n-1-2n-3，也就是s（n）=q（n）+v（n）=p（n）+u（n）。

对于其余的C2-C3个u（n），均存在v（n），使得LC5（s（n））=min[LC（p（n）+u（n）+v（n））]＜2n-1-2n-3。

③当a1，a2位于同一子序列，a3，a4而位于另外两个不同的子序列时，这样的u（n）个数为

然而，当a1，a2相距为2n-3的偶数倍时，这样的u（n）有个，其中a1，a2相距为2n-1的情况有个。a1，a2相距为2n-3的偶数倍且不为2n-1的u（n）个数,这时，存在1个不同于u（n）的v（n），WH（v（n））=5，使得LC（u（n）+v（n））＜2n-1-2n-3。

对于其余的C4-C5个u（n），均存在v（n），使得LC5（s（n））=min[LC（p（n）+u（n）+v（n））]＜2n-1-2n-3。

根据引理4，使得LC（p（n））=2n-1-2n-3的序列p（n）有22n-1-2n-3-1个。

综上所述，满足LC5（s（n））=2n-1-2n-3的非平衡周期二元序列s（n）的个数为

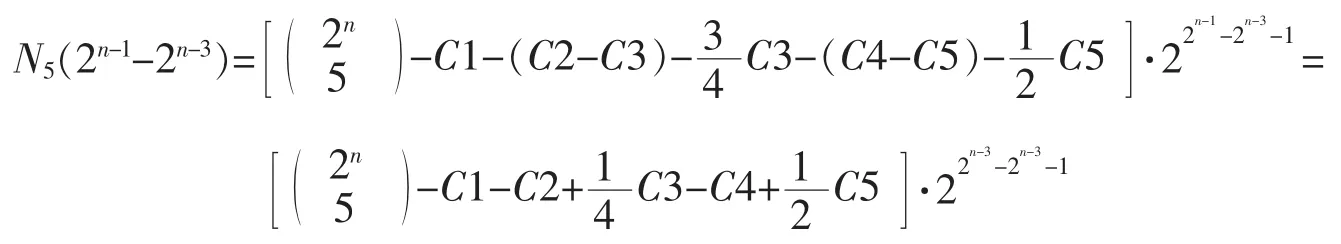
证毕。

例如：当n=5，LC5（s（n））=12时，N5（12）=19 922 944，与计算机编程检验结果一致。

基于Games-Chan算法，通过分析5-错线性复杂度已给定的序列的错误序列，利用组合排列的相关方法进行筛选，给出了5-错线性复杂度等于2n-3+x，2n-2-2n-m以及2n-1-2n-3时,周期和线性复杂度均等于2n的原序列s（n）的计数公式，并通过计算机编程给予验证。

[1]Berlekamp S R.Algebraic Coding Theory[M].New York：Mcgraw-Hill，1968.

[2]Games R A，Chan A H.A fast algorithm for determining the complexity of a binary sequence with period 2n[J].IEEE Transactions on Information Theory，1983，29（1）：144-146.

[3]Ding C，Xiao G，Shan W.The Stability Theory of Stream Ciphers[M].Berlin：Springer-Verlag，1991：85-88.

[4]Stamp M，Martin C F.An algorithm for thek-error linear complexity of binary sequences with period 2n[J].IEEE Transactions on Information Theory，1993，39（4）：1398-1401.

[5]苏明.周期序列复杂度的分布[D]．天津：南开大学，2004．

[6]Meidl W.On the stability of 2n-periodic binary sequences[J].IEEE Transactions on Information Theory，2005，51（3）：1151-1155．

[7]李鹤龄，戚文峰.Fp上Pn-周期序列的k-错误序列[J].通信学报，2010，31（6）：19-24.

[8]周建钦，刘军.2n-周期二元序列的3-错误序列分布[J].电子与信息学报，2012，34（8）：1923-1927.

[9]唐淼.2n-周期序列的k-错线性复杂度期望的界[J].巢湖学院学报，2011，13（3）：1-4.

[10]周建钦.具有2n线性复杂度的2n周期二元序列的3错线性复杂度[J].应用数学学报，2013，36（3）：399-413.

[11]周建钦,陈加如.2n-周期平衡二元序列的6-错线性复杂度[J].杭州电子科技大学学报，2011，31（6）：17-19.

The 5-error linear complexity of 2n-periodic unbalanced binary sequences

ZHOU Jianqin1，2，WANG Hongcui1
（1.Telecommunication School，Hangzhou Dianzi University，Hangzhou 310018，China；2.School of Computer Science&Technology，Anhui University of Technology，Ma'anshan 243032，China）

The linear complexity andk-error linear complexity have been used to measure randomness and stability of keystream sequences.They are extremely important for studying keystream strength.Studying error sequences with minimal Hamming weight is an effective method for calculating the number of sequences with the givenk-error linear complexity.Based on this method,counting functions ofs（n）with both period and linear complexity equal to 2nand 5-error linear complexity equal to 2n-3+x，2n-2-2n-mand 2n-1-2n-3are derived respectively. They are also verified by computer program.

keystream sequences；linear complexity；k-error linear complexity；k-error linear complexity distribution

TN918.1

A

1672-0687（2015）01-0001-07

责任编辑：艾淑艳

2013-09-25

国家自然科学基金资助项目（61272045）；安徽省自然科学基金资助项目（1208085MF106）

周建钦（1963-），男，山东巨野人，教授，硕士，研究方向：通信，密码学与理论计算机科学。