非完整系统基于El-Nabulsi分数阶模型的Noether对称性与摄动

陈菊，张毅

（1.苏州科技学院数理学院，江苏苏州215009；2.苏州科技学院土木工程学院，江苏苏州215011）

非完整系统基于El-Nabulsi分数阶模型的Noether对称性与摄动

陈菊1，张毅2*

（1.苏州科技学院数理学院，江苏苏州215009；2.苏州科技学院土木工程学院，江苏苏州215011）

El-Nabulsi针对非保守系统的建模提出了一类新的分数阶模型，即El-Nabulsi分数阶模型或类分数阶变分方法。文章研究该模型下线性非完整系统Noether对称性的摄动与绝热不变量问题，给出了该模型下线性非完整系统绝热不变量存在的条件及其形式。

非完整力学系统；El-Nabulsi分数阶模型；Noether对称性的摄动；绝热不变量

为研究非保守系统的动力学建模，El-Nabulsi[1-2]于2005年在分数阶微积分的框架下基于Riemann-Liouville分数阶积分定义提出了一种新的非保守动力学模型，即El-Nabulsi分数阶模型或类分数阶变分方法。在El-Nabulsi分数阶模型中，分数阶时间积分仅依赖于一个实参数α，所得到的Euler-Lagrange方程出现相应于耗散力的广义分数阶外力且不出现分数阶导数[3-6]。基于El-Nabulsi动力学模型的对称性与守恒量以及对称性的摄动与绝热不变量的研究已经取得了一些重要成果[7-12]。笔者将进一步研究线性非完整系统Noether对称性的摄动与绝热不变量问题。

1 El-Nabulsi变分问题与非完整系统的运动微分方程

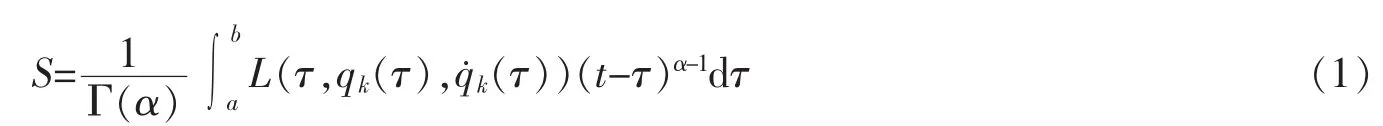
在固定边界条件

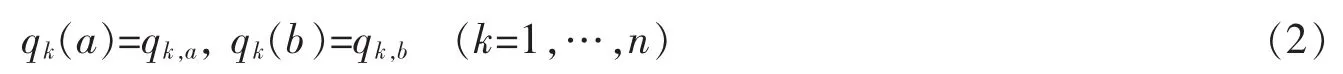
称上述变分问题为El-Nabulsi变分问题，泛函（1）为El-Nabulsi-Hamilton作用量。

假设系统的运动受有r个线性非完整约束

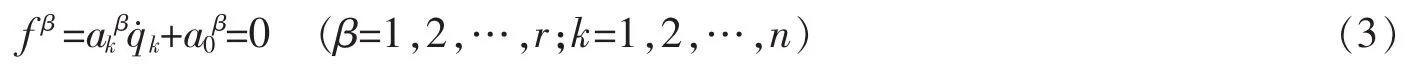
其中akβ和a0β是广义坐标qs，广义速度q˙s和时间t的函数。约束（3）对虚位移的限制条件为

假设力学系统的位形由n个广义坐标qk（k=1，…，n）来确定，El-Nabulsi提出的基于Riemann-Liouville分数阶积分的变分问题定义如下[7]：

求积分泛函

由El-Nabulsi-d’Alembert-Lagrange原理和条件（4），并利用Lagrange乘子法，可以得到[12]

其中λβ为约束乘子，（5）式为El-Nabulsi分数阶模型下线性非完整系统带乘子形式的运动微分方程。

2 Noether对称性与精确不变量

引进时间和广义坐标的无限小变换

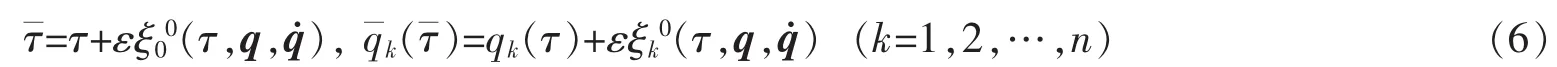
El-Nabulsi-Noether等式给出[11]

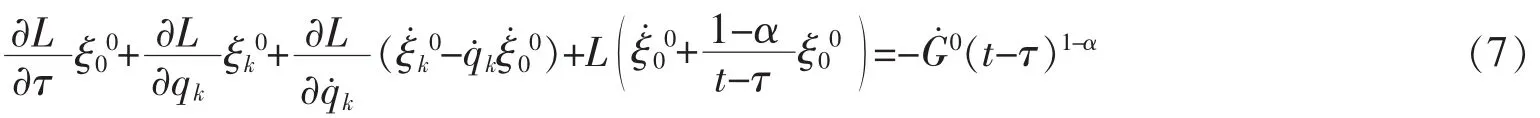
非完整约束对虚位移的限制条件（4）给出

定理1对于El-Nabulsi分数阶模型下未受扰的线性非完整系统（3）、（5），如果无限小变换的生成元ξ00，ξk0满足El-Nabulsi-Noether等式（7）和限制条件（8），则系统的Noether对称性直接导致精确不变量

3 Noether对称性的摄动与绝热不变量

如果El-Nabulsi分数阶模型下线性非完整系统（3）、（5）受到小扰动νQk的作用，那么系统原有的对称性与不变量将会在小扰动作用下相应地发生改变。系统的运动正轨满足的运动微分方程变为

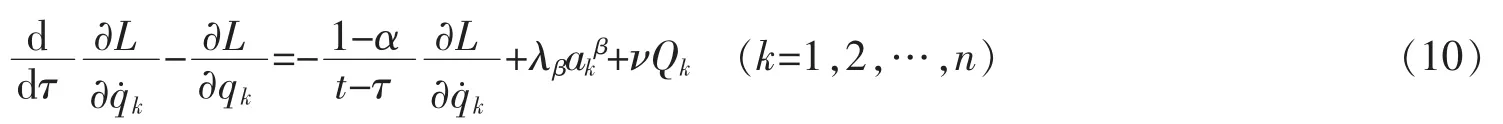
假设系统受到扰动后的无限小变换生成元ξ0，ξk是在系统未受扰动时的生成元基础上发生的小摄动，且规范函数G也相应地发生了小摄动，即有

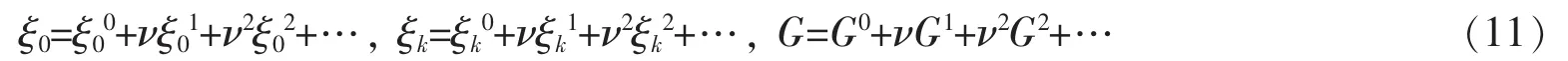
定理2El-Nabulsi分数阶模型下线性非完整系统（3）、（5）在受到小扰动νQk的作用下，如果存在规范函数，使无限小变换的生成元，满足

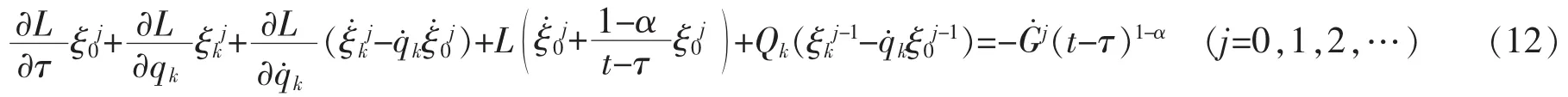
且满足限制条件

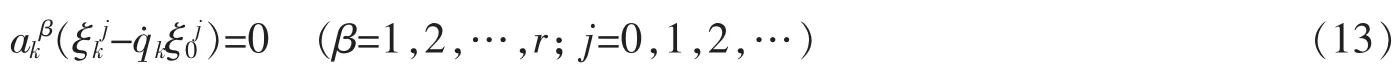
其中j=0时，约定ξ0-1=ξk-1=0，则

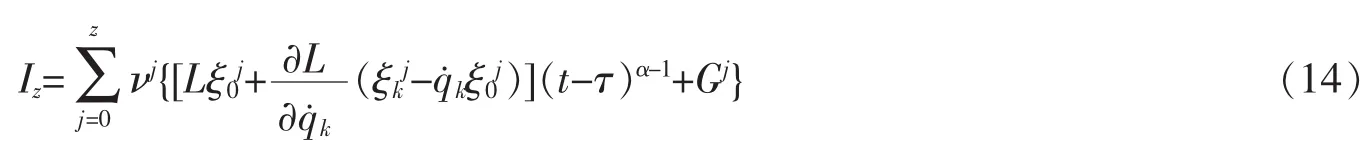
是该系统的一个z阶绝热不变量。

证明将Iz对时间τ求导数，利用方程（10），以及条件（12）和（13），得

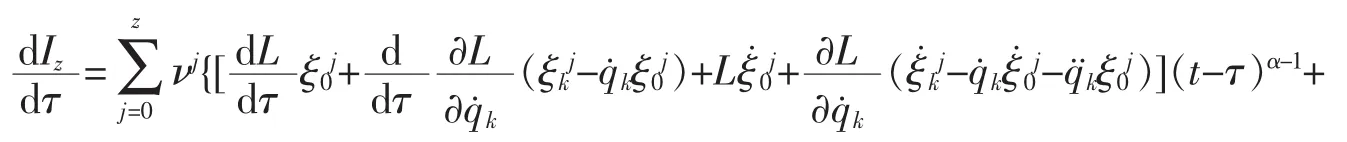
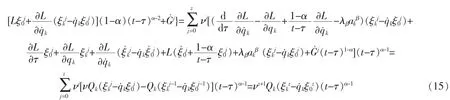
由绝热不变量定义[11]，可知Iz是El-Nabulsi分数阶模型下线性非完整系统的z阶绝热不变量。

4 算例

例系统Lagrange函数和所受的线性非完整约束分别为

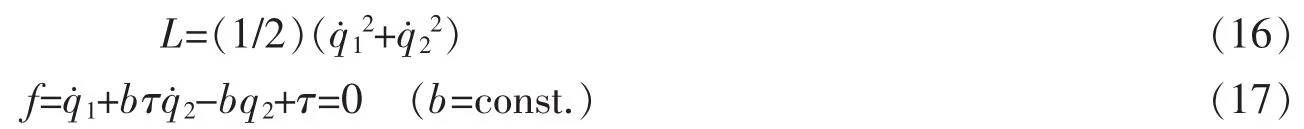
El-Nabulsi-Noether等式（7）和限制条件（8）式分别给出

联立方程（18）和（19）式，有如下解

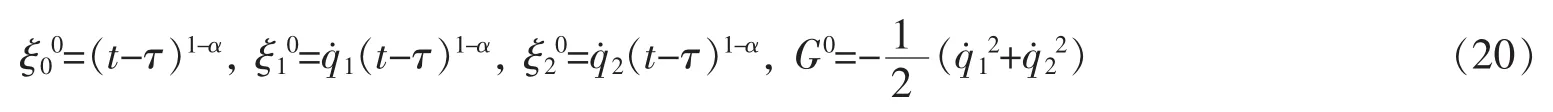
生成元（20）相应于El-Nabulsi分数阶模型下所论非完整系统的Noether对称性。由定理1，系统存在如下精确不变量

因此，相应于生成元（20）式的不变量是平庸的。假设系统受到的小扰动为

条件（12）式和限制条件（13）分别给出

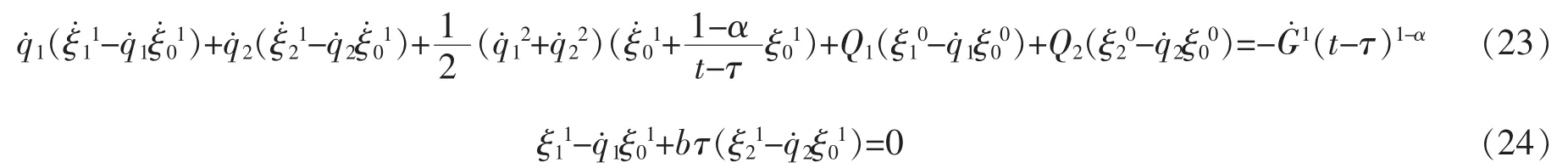
联立方程（23）和（24）式有如下解

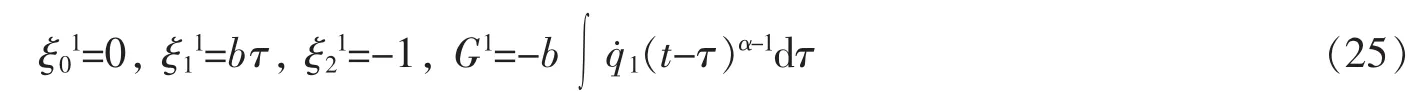
从式（20）和（25），由定理2得知系统存在如下一阶绝热不变量

进一步可求得系统的更高阶绝热不变量。

[1]El-Nabulsi A R.A fractional approach to nonconservative Lagrangian dynamical systems[J].Fizika A，2005，14（4）：289-298.

[2]El-Nabulsi A R.A fractional action-like variational approach of some classical，quantum and geometrical dynamics[J].Int J Appl Math，2005，17（3）：299-317.

[3]El-Nabulsi A R.Necessary optimality conditions for fractional action-like integrals of variational calculus with Riemann-Liouville derivatives of order（a，b）[J].Math Methods Appl Sci，2007，30：1931-1939.

[4]El-Nabulsi A R.Fractional action-like variational problems in holonomic，non-holonomic and semi-holonomic constrained and dissipative dynam-ical systems[J].Chaos，Solitons and Fractals，2009，42：52-61.

[5]El-Nabulsi A R.Fractional variational problems from extended exponentially fractional integral[J].Applied Mathematics and Computation，2011，217：9492-9496.

[6]El-Nabulsi A R.Universal fractional Euler-Lagrange equation from a generalized fractional derivate operator[J].Central European Journal of Physics，2011，9（1）：250-256.

[7]张毅.相空间中类分数阶Noether对称性与守恒量[J].中山大学学报：自然科学版，2013，52（4）：20-25.

[8]Long Z X，Zhang Y.Noether’s theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space[J].Acta Mech，2014，225（1）：77-90.

[9]Chen J，Zhang Y.Perturbation to Noether symmetries and adiabatic invariants for disturbed Hamiltonian systems based on El-Nabulsi nonconservative dynamics model[J].Nonlinear Dynamics，2014，77：353-360.

[10]陈菊，张毅.El-Nabulsi模型下Birkhoff系统Noether对称性的摄动与绝热不变量[J].物理学报，2014，63（10）：104501.

[11]张毅.非保守动力学系统Noether对称性的摄动与绝热不变量[J].物理学报，2013，62（16）：164501.

[12]Zhang Y，Zhou Y.Symmetries and conserved quantities for fractional action-like Pfaffian variational problems[J].Nonlinear Dynamics，2013，73（1-2）：783-793.

Noether symmetries and perturbation for nonholonomic systems based on El-Nabulsi fractional order models

CHEN Ju1，ZHANG Yi2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

El-Nabulsi put forward a new method of modelling nonconservative dynamic systems in 2005,which was called El-Nabulsi fractional order model or fractional action-like variational approach.This paper studies the perturbation of Noether symmetries and adiabatic invariants for a linear nonholonomic system based on this model.The conditions for the adiabatic invariants were given and their formulation was presented.

nonholonomic mechanical system；El-Nabulsi fractional order model；perturbation of Noether symmetry；adiabatic invariants

O316MR（2000）Subject Classification：00A69

A

1672-0687（2015）01-0008-04

责任编辑：谢金春

2014-09-23

国家自然科学基金资助项目（10972151；11272227）；江苏省普通高校研究生科研创新计划立项项目（CXLX13_855）；苏州科技学院研究生科研创新计划资助项目（SKCX13S_050）

陈菊（1987-），女，安徽宿州人，硕士研究生，研究方向：力学中的数学方法。*