分数阶Chen 系统的分析、同步及其保密通信实现
2015-01-08贾红艳陈增强
贾红艳,陶 倩,陈增强,薛 薇
(1.天津科技大学电子信息与自动化学院,天津 300222;2.南开大学自动化系,天津 300071)
近几十年来,随着很多系统表现出分数阶动力学行为,关于分数阶微积分在物理以及工程上的应用研究正逐渐成为新的研究热点[1].这不仅丰富了有着300 多年历史的分数阶微积分理论的研究内容,而且也为分数阶混沌理论及应用的研究提供了新的动力和技术手段,进而促进了分数阶混沌理论及应用的发展,使得在更低维的系统中发现混沌动态成为可能.一些分数阶系统的混沌特性相继被发现[2-4],这些研究工作往往通过吸引子相轨迹、系统稳定性分析、Lyapunov 指数和拓扑马蹄分析等方法,分别从理论和数值分析角度对分数阶系统的混沌动态进行分析或验证.同时,为了丰富和发展分数阶混沌研究,也基于混沌应用的需要,关于分数阶混沌系统的电路实现[5-7]、同步及控制研究[8-10]、图像及信息加密研究等[11-12]方面也逐渐吸引了人们越来越多的关注.尤其在图像及信息加密方面,由于混沌系统具有对初始条件的敏感性、长期不可预测性、隐蔽性以及高度的复杂性,非常适合于保密通信等研究领域.近年来,整数阶混沌同步在保密通信、扩频通信中的应用被广泛关注[13-14],但多数研究都停留在仿真阶段,未能进行硬件电路的实现及实际的应用研究.另外,分数阶混沌系统在保密通信中比整数阶具有更加复杂的动力学行为,所以其在保密通信领域是一个很有潜力的发展方向,但目前针对分数阶混沌系统的保密通信研究则涉及更少,即使涉及也多停留在仿真阶段.基于目前的研究现状,本文首先采用频域近似方法研究了分数阶Chen 系统的混沌特性,与上述对其混沌特性的研究相比,进一步给出了随着参数变化的Lyapunov 指数谱图,解释了其分形,发现了更为丰富的动态特性.然后基于一类整数阶混沌观测器的设计方法[15-16],设计了基于观测器的分数阶Chen 系统的混沌同步控制策略;另外,也基于一种分数阶近似电路的实现方法[17],用模拟电路实现了该同步控制.最后将其运用到混沌掩盖的保密通信中,证明该同步控制及其保密通信方法的可行性.
1 分数阶Chen系统的混沌分析及同步控制
1.1 分数阶Chen系统的混沌分析
2004 年,Li 和Chen 利用频域近似方法,分析了分数阶Chen 系统的混沌动态[3],该系统可描述为

式中:a、b、c 是系统参数;α、β、γ 为阶次.
2006 年,Lu 等[18]采用同样的近似方法进一步分析了该系统的混沌特性,给出了不随系统参数变化的部分Lyapunov 指数值.在上述研究工作的基础上,本文将继续研究α=β=γ=0.9时,分数阶Chen 系统的混沌特性.当选取系统变量b=3 和c=28,系统阶次α=β=γ=0.9时,基于 Lyapunov 指数的Jacobian 计算方法,本文得到了系统随a 变化的Lyapunov 指数谱图和分岔图,如图1 所示.
图1 中Lyapunov 指数谱图和分岔图是一致的,通过对图1 中的Lyapunov 指数谱图分析可以发现,当大致选取 a∈(32.9,46.0)时,系统的最大Lyapunov指数大于零,系统会呈现混沌状态;当a∈(30.0,30.8)和a∈(31.1,31.9)时,系统的最大Lyapunov 指数等于零,系统会出现周期的动态特性.现从系统展现混沌特性的参数区间和展现周期特性的参数区间分别选取a=35 和a=30,b=3,c=28,β=γ=0.9时,可以发现分数阶Chen 系统的混沌吸引子和周期吸引子,其中x-y 平面的相轨迹如图2 所示.

图1 分数阶Chen系统的 Lyapunov指数谱图和分岔图Fig.1 Lyapunov exponents diagram and bifurcation diagram of the fractional-order Chen system
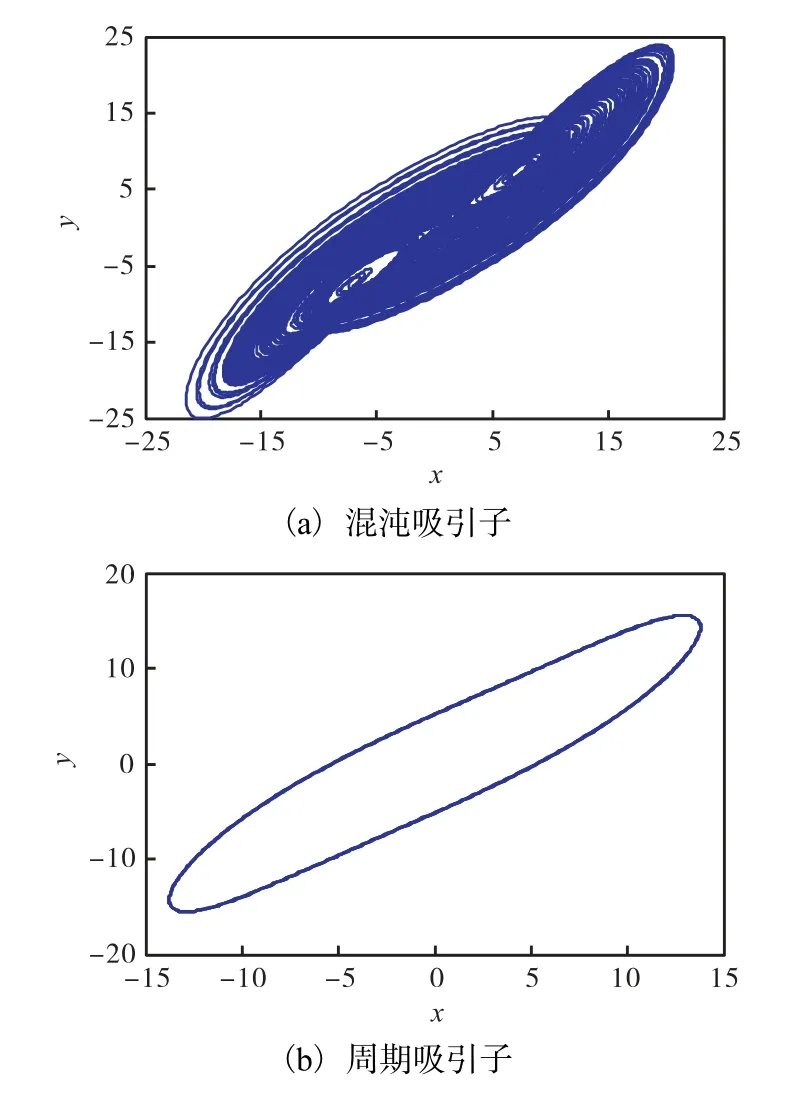
图2 分数阶Chen系统的相轨迹Fig.2 Attractors of the fractional-order Chen system
上述的数值仿真分析进一步验证了通过对Lyapunov 指数和分岔图分析所得到的结论.考虑到信息加密的需要,本文将主要研究该系统在混沌区间的电路实现和同步控制问题.
1.2 分数阶Chen系统的同步控制
根据文献[15-16]中给出的基于观测器反馈的一类整数阶混沌系统的同步原理,本文设计了分数阶Chen 系统在混沌状态的同步控制,首先在系统处于混沌状态区间选取参数,即a=35,b=3,c=28,α=β=γ=0.9 时,且以 x1、x2、x3作为驱动系统的状态变量,得到如式(2)所示的驱动系统.

将式(2)按文献[15]和[16]中定理所述写为

其中

根据文献[15]和[16]给出的定理,如果能找到A-D的特征值均具有负实部,则=Ay +B F(y)+C+u(x)-u(y)为驱动系统的一个同步观测器,根据所得到当 d1=d2=0,d3=50时,A-D 的特征值为λ1=-3,λ2=λ3=-28.5±j12.239,满足同步条件,所以相应的同步响应系统为
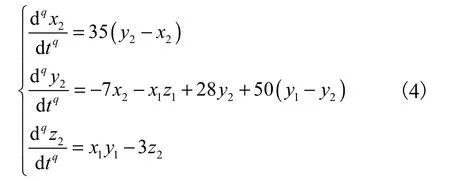
在选取驱动式(2)系统的状态变量初始值为(3,-6,7),式(4)响应系统的状态变量初始值为(3,0,0)时,可观察到系统的同步结果如图3 所示.通过分析图3 可以得到结论:本文所设计的基于观测器的分数阶Chen 系统的同步控制,可以使该系统及其响应系统在零时刻达到同步,响应快速性较好.
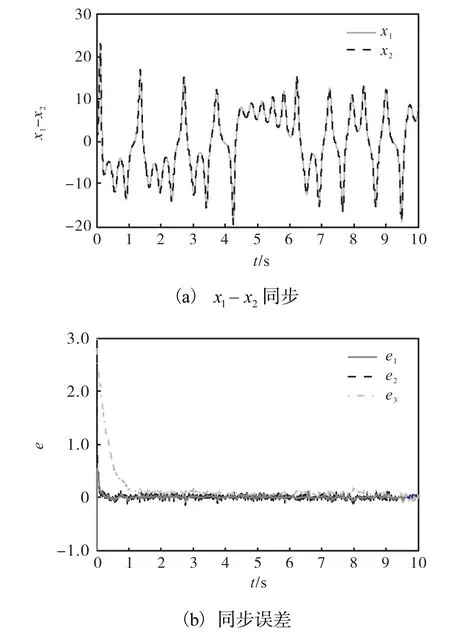
图3 分数阶Chen系统的同步结果Fig.3 Synchronization results of the fractional-order Chen system
2 分数阶Chen系统同步的电路实现
基于改进型电路模块化设计方法和频域近似方法设计了基于观测器的分数阶Chen系统的同步模拟电路,见图4.在同步模拟电路中采用的器件分别为线性电阻、线性电容、运算放大器LF347N以及模拟乘法器AD633.其中,R1=R2=R10=R11=286,Ω,R3=R13=1.43,kΩ,R4=R7=R15=R18=100,Ω,R5=R14=357,Ω,R6=R17=3.3,kΩ,R12=R16=200,Ω,R8=R9=R19=R20=10,kΩ,R21=R24=R27= R30= R33= R36=1.55,MΩ,R22= R25= R28=R31= R34= R37=62,MΩ,R23=R26=R29= R32=R35= R38=2.5,kΩ,C1= C4= C7= C10= C13= C16=0.73 μF,C2= C5= C8= C11= C14= C17=0.52 μF,C3= C6= C9= C12= C15= C18=1.1 μF;0.73 μF 的电容用2 个0.15 μF、1 个0.1 μF、1 个0.33 μF 的电容并联代替,0.52 μF 的电容用2 个0.15 μF 与1 个0.22 μF 的电容并联代替,1.1 μF 的电容用1 μF 与0.1 μF的电容并联代替.

图4 分数阶Chen系统的同步电路实现Fig.4 Implementation of fractional-order Chen system in synchronization circuit
在搭建好模拟电路后,首先用模拟示波器观察驱动和响应系统的吸引子相轨迹,发现这两个系统都呈现混沌状态,满足进行混沌同步控制的条件,这里只给出驱动系统的在x1-y1平面的混沌吸引子相轨迹(图5),响应系统的混沌吸引子相轨迹与其是一样的,不再赘述.然后,在驱动和响应系统均呈现混沌特性的状态下,用模拟示波器观察到了驱动和响应系统之间的同步.图6 为驱动系统的状态变量x1与响应系统的状态变量 x2之间的同步图.基于观测器方法的分数阶Chen 系统能够达到很好的同步结果,为其在混沌保密通信中的应用奠定了基础.
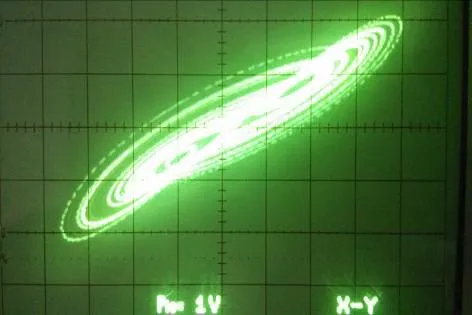
图5 示波器观测到的驱动分数阶Chen 系统的x1-y1混沌吸引子Fig.5 Chaotic attractors observed by oscilloscope in x1-y1plane of drive fractional-order Chen system

图6 分数阶Chen系统基于观测器反馈的x1-x2同步结果Fig.6 x1-x2synchronization results of fractional-order Chen system based on state observers’ feedback
3 分数阶Chen系统的保密通信实现
在上述已实现的同步电路基础上,分别将驱动系统的3 个状态变量x1、y1、z1作为驱动载波信号,原始的模拟信号作为待加密的信号,加载到驱动载波信号中生成合成信号,进行模拟信号传输.然后,在信号的输出端利用响应系统的3 个对应的状态变量x2、y2、z2与传输过来的合成信号进行解密,得到还原信号.首先选择待加密的原始信号为正弦信号,然后以同步模拟电路的状态变量x1为驱动载波信号,以同步模拟电路的响应信号 x2为解密信号,进行加密研究,电路如图7 所示.其中运算放大器选用LF347N,电阻R39=R40=R41=R42=R43=R44=10,kΩ,最后通过模拟示波器观察到了较好的信息加密效果,即得到了与原始信号一致的还原信号,如图8 所示.通过模拟电路实验表明,本文所设计及实现的分数阶Chen 系统的同步是可行的,可以利用其进行信息加密工作.

图7 分数阶Chen系统保密通信研究的模拟电路实现Fig.7 Implementation of the study of fraction-order Chen system in the analog circuit of confidential communications

图8 保密通信实验结果Fig.8 Experimental results of confidential communication
4 结语
本文基于观测器反馈控制原理设计了分数阶Chen 系统的同步控制.在通过数值仿真验证了其同步效果后,又用模拟电路实现了该同步控制,电路实验的结果和数值仿真的结果一致.最后,基于混沌掩盖技术,利用分数阶Chen 系统的同步电路进行了信息加密研究,解密后的信号与原始待加密的信号是一致的,表明本文所设计及实现的分数阶Chen 系统的同步是可行的,可以利用其进行信息加密工作.本文的工作丰富了混沌信息加密的研究工作,为混沌加密提供了新的模型和技术手段.
[1]Charef A,Sun Y Y,Tsao Y Y,et al.Fractal system as represented by singularity function[J].IEEE Transaction on Automatic Control,1992,37(9):1465-1470.
[2]Ge Zhengming,Qu Chanyi.Chaos in a fractional order modified Duffing system[J].Chaos Solitons &Fractals,2007,34(2):262-291.
[3]Li Chunguang,Chen Guanrong.Chaos and hyperchaos in the fractional-order Rössler equations[J].Physica A:Statistical Mechanics and its Applications,2004,341∶55-61.
[4]Grigorenko I,Grigorenko E.Chaotic dynamics of the fractional Lorenz system[J].Physical Review Letters,2003,91(3):034101-1-034101-4.
[5]贾红艳,陈增强,薛薇.分数阶Lorenz 系统的分析及电路实现[J].物理学报,2013,62(14):140503-1-140503-7.
[6]Han Qiang,Liu Chongxin,Sun Lei,et al.A fractional order hyperchaotic system derived from Liu system and its circuit realization[J].Chinese Physics B,2013,22(2):020502-1-020502-6.
[7]Jia Hongyan,Chen Zengqiang,Qi Guoyuan.Topological horseshoe analysis and circuit realization for a fractionalorder Lü system[J].Nonlinear Dynamics,2013,74(1/2):203-212.
[8]Wang Sha,Yu Yongguang,Wang Hu,et al.Function projective lag synchronization of fractional-order chaotic systems[J].Chinese Physics B,2014,23(4):040502-1-040502-7.
[9]Wang Junwei,Ma Qinghua,Zeng Li.Observer-based synchronization in fractional-order leader :Follower complex networks[J].Nonlinear Dynamics,2013,73(1/2):921-929.
[10]Xue Wei,Xu Jinkang,Cang Shijian,et al.Synchronization of the fractional-order generalized augmented Lü system and its circuit implementation[J].Chinese Physics B,2014,23(6):060501-1-060501-8.
[11]Deng Lei,Cheng Mengfan,Wang Xiaolong,et al.Secure OFDM-PON system based on chaos and fractional Fourier transform techniques[J].Journal of Lightwave Technology,2014,32(15):2629-2635.
[12]Xu Yong,Wang Hua,Li Yongge,et al.Image encryption based on synchronization of fractional chaotic systems[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(10):3735-3744.
[13]Long Min,Qiu Shuisheng.Application of periodic orbit theory in chaos-based security analysis[J].Chinese Physics,2007,16(8):2254-2258.
[14]闵富红,王恩荣.超混沌Qi 系统的错位投影同步及其在保密通信中的应用[J].物理学报,2010,59(11):7657-7662.
[15]周平.一类3 维连续混沌系统观测器[J].物理学报,2003,52(5):1108-1111.
[16]蒲兴成.混沌同步控制及应用研究[D].重庆:重庆大学,2006.
[17]刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报,2007,56(12):6865-6873.
[18]Lu Junguo,Chen Guangrong.A note on the fractionalorder Chen system[J].Chaos,Solitons &Fractals,2006,27(3):685-688.
