基于AHP-FCE的浓缩装置优选

江 科，姚中亮

（1.长沙矿山研究院有限责任公司，湖南 长沙 410012；2.国家金属采矿工程技术研究中心，湖南 长沙 410012；3.金属矿山安全技术国家重点实验室，湖南 长沙 410012）

基于AHP-FCE的浓缩装置优选

江 科1，2，3，姚中亮1，2，3

（1.长沙矿山研究院有限责任公司，湖南 长沙 410012；2.国家金属采矿工程技术研究中心，湖南 长沙 410012；3.金属矿山安全技术国家重点实验室，湖南 长沙 410012）

放砂浓度的稳定性是充填系统正常运行的核心指标，制约着充填体的质量，对充填站尾砂浓缩储存装置进行优选就显得格外重要。但优选过程涉及大量只能定性无法定量的因素，使得采用常规手段无法准确得出结论。利用模糊数学的相关理论可以很好地完成此类决策，通过层次分析法（AHP）确定各因素所占权重，再由模糊综合评价法（FCE）评定各方案的综合优越度。通过对江西某钨矿进行研究，根据现场条件制定方案Ⅰ、Ⅱ和Ⅲ，计算出各方案的最终优越度分别为70.5%、72.2%和74.8%，从而确定方案Ⅲ更优。结果表明，AHP-FCE可以很好地解决金属矿山尾砂浓缩存储装置的选择工作，为钨矿山充填系统的设计提供了一种可行的思路。

砂仓类型；层次分析法；模糊综合评价法；权重向量

0 引言

随着国家对环保问题的重视，矿山企业希望最大程度地提高资源回收利用率，充填采矿法逐步成为矿山企业首选。充填系统各环节的良好衔接是保证充填采矿法安全与高效不可或缺的条件。放砂浓度与其稳定性是评价一座地上充填站最关键的指标。若流动性良好，放砂浓度与单位充填体中消耗的胶结剂量成反比，浓度越高，成本越低；放砂浓度波动小，能提高系统运行效率，最大限度地支持井下采矿安全进行。尾砂储存与浓缩装置选择得恰当与否，直接关系到放砂浓度与稳定性，间接影响充填采矿法的高效运行，对尾砂储存与浓缩装置的研究就显得极其重要。如江西某钨矿由于多年来使用空场法，导致遗留大量高品位矿柱无法回采，并且空区面积达200多万m3，若继续沿用以前的开采方法将不能保证矿山安全与资源的高效回收利用[1]。该矿山急需建设一套地面充填系统来实行充填采矿法并同时充填地下采空区，以保证采矿安全与高品位矿柱的回采。但由于该白钨矿选矿工艺复杂，尾砂浆性质也极其复杂[2]，不但不能很好地沉降，还在运动过程当中产生大量的夹杂着细颗粒尾砂的泡沫。该矿的尾砂沉降与浓缩是充填系统建设过程中的一大难点，能否解决直接决定充填系统的能力与效率。若能成功解决，将对钨矿山的充填站建设提供很好的指导作用。

影响充填站尾砂浓缩装置类型选择的因素众多，如造价、工艺复杂程度、场地、检修清洗难易程度、尾砂性质、运营成本等。其决定着矿山充填能力、效率、采矿工艺安全性等，因此浓缩储存装置选择的合理性将直接决定矿山充填采矿前景，与矿山生产的有序进行产生直接联系[3]。因浓缩储存装置类型的选择涉及众多因素、指标，在决策的过程中，不能断然由某一条件进行选择，需考虑众多制约条件的综合影响。由于不能定量衡量每个指标的权重，需要定性描述各影响因素，同时兼顾不可预见的因素，可知选择的过程是模糊决策[4]。

对实际情况的判断通常会受到经验的影响，目前在某些矿业工程中运用模糊综合评价法（FCE）对采矿方案进行决策，为复杂难采矿体的采矿设计提供了理论依据，为本文浓缩装置的选择提供指导。为克服FCE选取权重仅通过专家主观评审的弊端，并全面考虑影响浓缩装置选择的各种因素，使方案更符合实际，评价结果更可靠，本文将层次分析法（AHP）和模糊综合评价法（FCE）[5]结合应用到决策中，建立浓缩储存装置综合指标体系，再利用AHP全面确定各因素的权重，最后根据FCE确定最优的装置类型[6-7]。

1 AHP-FCE原理

层次分析法（AHP）是将定性分析和定量分析相结合，把人们的思维过程层次化和数量化的多准则思维的方法，在目标结构复杂且缺乏必要数据的情况下尤为实用。模糊综合评价法（FCE）是根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它是综合评价方法，具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。

1．1 构建评价指标体系

构建评价体系直接决定评估的准确性，是进行方案决策的基础。评价应选取最为突出和关键的指标，构造出一个层次性的结构模型，为决策服务[8]。利用AHP基本原理，可建立尾砂浓缩储存装置选择方案综合指标体系O-P-X。

1．2 权重分配

由于各影响因素侧重点不同，对决策过程的重要性有差别，所以需要分配各因素的权重，AHP能较完善地解决这个问题。

（1）根据模糊数学构造比较标度[9]，如表1。

表1 1～9标度的意义Tab．1 Meanings of the 1～9 scale

（2）构造判断矩阵A。

根据表1得到不同因子的数字标度，如Xi和Xj（i，j=1，2，3，…，n），求得其比值aij，定义A=（aij）m×m，A即为所求判断矩阵[10]，如式（1）。

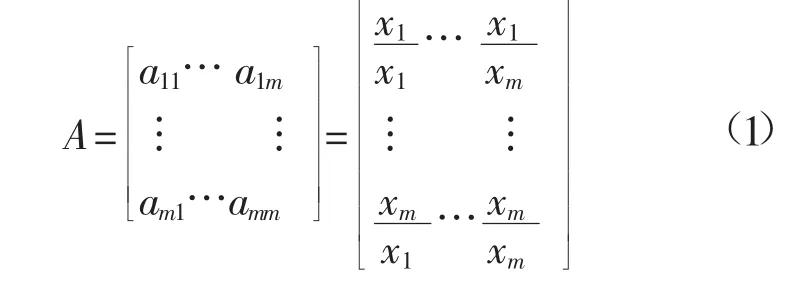
求解判断矩阵A特征根可得到各因素的相对权重，即求解AW=λmaxW，具有唯一的λmax和W，将W正规化后可得权重。可以证明，对于判断矩阵A，其最大特征值λmax存在且唯一，W由正分量组成，除相差常数倍数外，W是唯一的。本质上求W是计算权向量，对判断矩阵A很难求出精确的特征根和特征向量，只能求它们的近似值。本文采用和法计算权向量。

和法的原理：对于一致性判断矩阵，每一列归一化后就是相应的权重；对于非一致性判断矩阵，每一列归一化后近似其相应的权重。计算方法如公式（2）。

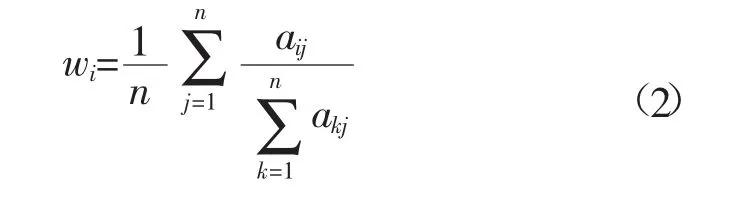
（3）一致性检验。

由于每个人主观经验有差别，客观实际较理想情况更为复杂，认识上受许多不稳定因素的干扰，所以致使判断矩阵存在一定误差。因此在决策过程中要对判断矩阵进行一致性检验。若判断矩阵无法通过一致性检验，则此判断矩阵不具有合理性，无法继续根据此结果对方案进行分析[11]。

判断矩阵的一致性检验公式为：CR=CI/RI。其中：CI为一致性检验指标，CI=（λmax-n）/（n-1）；n为判断矩阵的阶数；RI值可查询平均随机一致性指标表[8]。

若计算得到CR＜0.1，则A具有良好的一致性，否则矩阵A就不具有合理性，需重新反馈到决策者进行调整。

（4）计算权重向量。

完成上述步骤后，则可由AHP求得权重值。

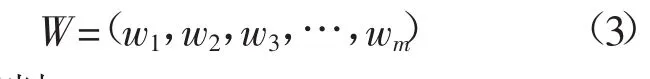
1．3 模糊综合评判

将定性条件转变为定量指标将会使决策的过程更加方便可靠。FCE根据隶属度理论能很好地实现这一目标，利用模糊数学转换指标，使得结果清晰，能较好地解决含有众多不确定因素的问题[12]。

由因素集到评价集的模糊映射f可诱导出模糊关系R，如式（4）。

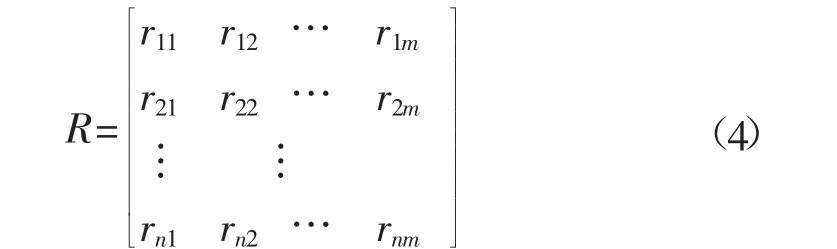
R即为隶属度矩阵。为使各指标具有可比性，需对指标两种进行无量纲化处理，其中定量指标由实际数据得来，定性指标由定量语气标度来确定，可以通过查询语气算子与定量标度相对隶属度关系表2来得到[13-15]。在充填系统尾砂浓缩储存装置的选择指标中，造价为定量指标，运营成本、场地要求、尾砂物理化学性质、放砂浓度、自动化程度、有效容积利用率、检修清洗难易程度、工作效率为非定量指标。

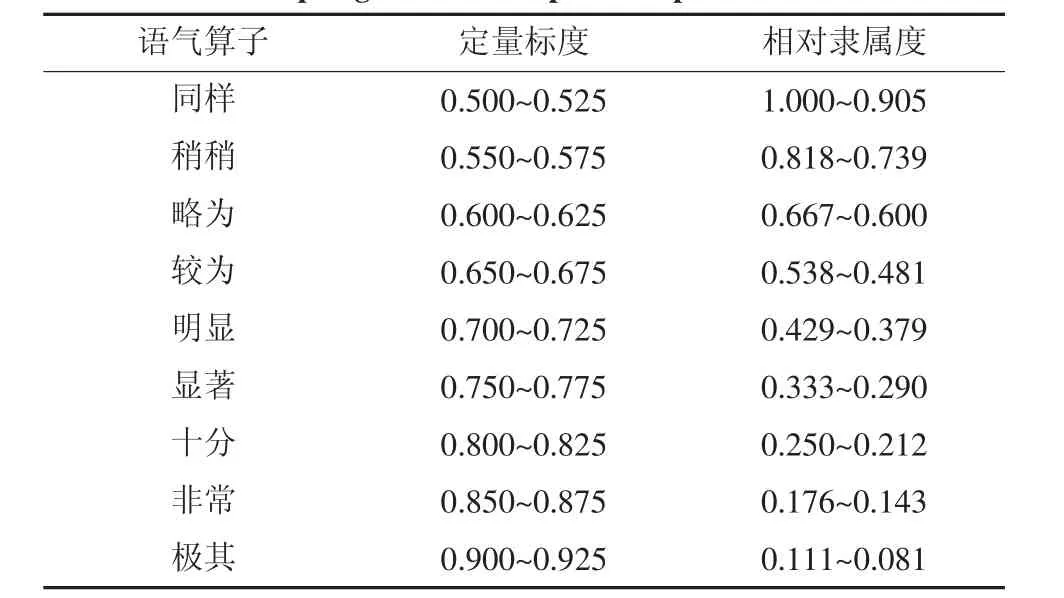
表2 语气算子与定量标度相对隶属度关系表Tab.2 Membership degrees between particle operator and ration mark

方案集的综合评价由隶属度矩阵R和因素权重W得到，见式（5）。

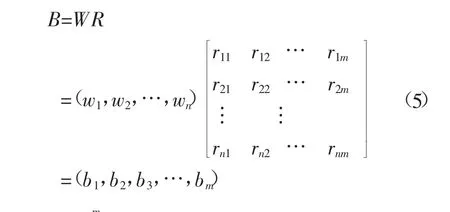
2 模型构建

用层次分析法基本原理，可建立砂仓类型选择方案综合（O）指标体系：

一是经济指标（P1），可以从造价（X1）、运营成本（X2）等分析；

二是现场条件指标（P2），可以从场地要求（X3）、尾砂物理化学性质（X4）等分析；

三是技术指标（P3），可以从放砂浓度（X5）、有效容积利用率（X6）、检修清洗难易程度（X7）、工作效率（X8）等分析。

须指出的是，在具体评价过程中，应根据实际要求对这些指标有所删减。

筹备建设充填站的矿山需根据现场考察及专家商议，确定适用的尾砂浓缩储存装置，目前国内矿山采用较多的为立式砂仓、卧式沙池、带式过滤机和深锥浓密机等，其中带式过滤机由于跟充填系统配合度较差、能耗过大等原因首先排除。对剩下的三个方案运用AHP和FCE进行优选。设定方案Ⅰ：卧式砂池；方案Ⅱ：立式砂仓；方案Ⅲ：深锥浓密机。构造一个层次结构模型，然后应用AHP对方案进行决策，该矿浓缩装置类型选择结构模型如图1。

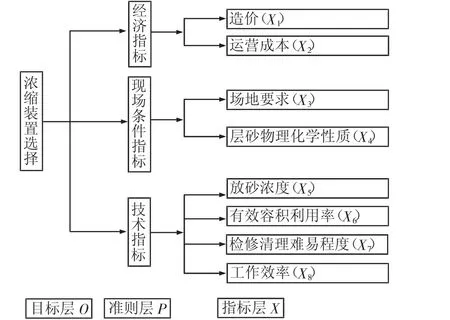
图1 浓缩装置选择结构模型Fig.1 Selection structure model of concentration device

根据矿山实际运营状况，分别构造O-P和P-X的判断矩阵，对判断矩阵进行一致性检验，最终计算出各因素的权向量。由权向量与隶属度矩阵可计算出三个方案的优越度，即可进行决策。

3 应用实例分析

以江西某钨矿尾砂浓缩储存装置类型选择方案为例，制定了综合评价指标，见表3。

表3 各方案综合评价指标体系Tab.3 Comprehensive evaluation system for each program

3.1 确定各因素权重分配

运用APH构造O-P的判断矩阵如表4，其中P1与P2重要程度相当，P3比P1、P2稍显重要。

根据得到的权重值，可得O-P判断矩阵特征值λmax0=3.000，查表2可得RI0=0.58，则得CI0=0，CR0= 0＜0.1。因此，O-P判断矩阵满足一致性检验要求。权重矩阵O=[0.250，0.250，0.500]可接受。

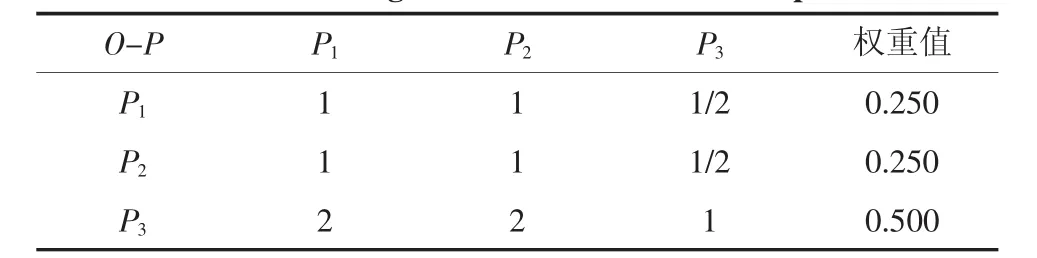
表4 O-P判断矩阵Tab.4 Judge matrix of O-P membership

同理，可按上述方法计算下述权重值：

P1-X：P1=[0. 7，0.3 ]，λmax1=2，CI1=0，RI1=0，CR1= 0＜0.1；

P2-X：P2=[0. 1，0.9 ]，λmax2=2，CI2=0，RI2=0，CR2= 0＜0.1；

P3-X：P3=[0.58，0.12，0.05，0.25 ]，λmax3=4.000，CI3=0，RI3=0.89，CR3=0＜0.1；

根据上述O-P判断矩阵得到P1、P2、P3的权重值。再由P-X矩阵得到X1、X2关于P1的权重值；X3、X4关于P2的权重值；X5、X6、X7、X8关于P3的权重值。相应的权重值相乘即得到如表5的层次总排序。

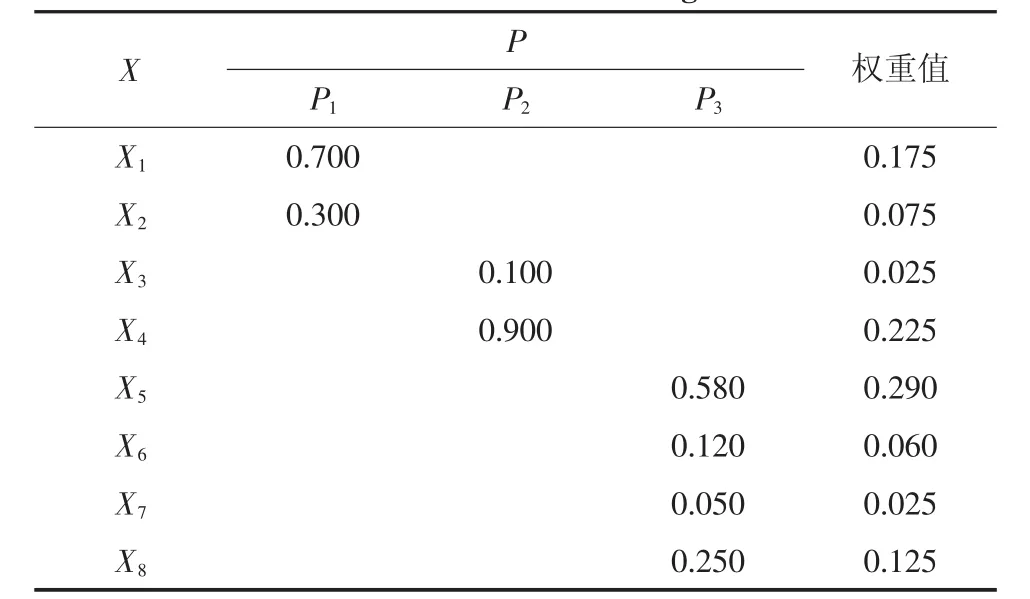
表5 层次总排序Tab.5 Total level sorting

得出总排序后，仍然需要对一致性进行检验：CI=0，RI=0.445，CR=0＜0.1；

故判断矩阵满足一致性检验要求，可得权重向量：W=（0.175，0.075，0.025，0.225，0.290，0.060，0.025，0.125）。

3.2 隶属矩阵确定

通过查询语气算子与定量标度相对隶属度关系表（表2），对综合评价指标表（表3）中的定量以及非定量指标进行隶属度确定，可得综合隶属度矩阵：

3.3 综合评价及结果

由上述权重向量与隶属度矩阵可得方案集的综合评价向量：

B=WR=（0.705，0.722，0.748）

由此可知b3＞b2＞b1，方案的优劣顺序为：方案Ⅲ＞方案Ⅱ＞方案Ⅰ，即深锥浓密机比立式砂仓和卧室沙池更加适合此矿山充填系统。

4 结论

（1）AHP和FCE能全面考虑影响充填站尾砂浓密储存装置选择的各种不确定因素，能够使决策者作出更为科学、准确、有理论依据的判断。

（2）运用AHP和FCE对江西某钨矿进行实例分析，构建综合评价模型，得出方案集的综合评价向量为（0.705，0.722，0.748），进而根据优越度选取方案Ⅲ。

（3）结果表明，AHP-FCE可以很好地解决金属矿山尾砂浓缩存储装置的选择工作，为钨矿山充填系统的设计提供了一种可行的新思路。

（4）AHP-FCE能够很好地解决由于因素过多而导致的权重难以分配的难题，很好地避免了因为人的主观性以及片面性而导致的决策失误。该方法可以在充填站建设方案的决策上起到很重要的作用。参考文献：

[1] 胡静云，林 峰，彭府华，等.香炉山钨矿残采区地压灾害微震监测技术应用分析 [J].中国地质灾害与防治学报，2010，（4）：109-115.

HU Jing-yun，LIN Feng，PENG Fu-hua，et al.Research on application of Microseismic monitoring technology on ground pressure hazard of residual are in Xianglushan tungstenmine[J]. The Chinese Journal of Geological Hazard and Control，2010，（4）：109-115.

[2] 刘清高，韩兆元，管则皋.白钨矿浮选研究进展[J].中国钨业，2009，24（4）：23-27.

LIU Qing-gao，HAN Zhao-yuan，GUAN Ze-gao.Research progress on scheelite flotation technology[J].China Tungsten Industry，2009，24（4）：23-27.

[3] 饶运章.降低胶结充填成本的途径及应用[J].中国矿业，1997，（33）：35-38.

RAO Yun-zhang.Ways and their applications for reducation cementing fill cost[J].China Mining Magazine，1997，（33）：35-38.

[4] 李俊芳，吴小萍.基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报：交通科学与工程版，2007，（2）：205-208.

LI Jun-fang，WU Xiao-ping.Synthetic evaluation for urban rail transit line network planning scheme based on AHP-FUZZY method [J].Journal of Wuhan University of Technology：Transportation Science and Engineering，2007，（2）：205-208.

[5] 赵伏军，谢世勇，杨 磊，等.基于层次分析法—模糊综合评价（AHP-FCE）模型优化矿井通风系统的研究[J].中国安全科学学报，2006，（4）：91-96.

ZHAOFu-jun，XIEShi-yong，YANGLei，etal.Study on optimization of mine ventilation system based on AHP-FCE model[J].China Safety Science Journal，2006，（4）：91-96.

[6] 杨纶标，高英仪，等.模糊数学原理及应用[M].华南理工大学出版社，2011.

[7] 郭嗣琮.工程应用软计算[M].中国矿业大学出版社，2009.

[8] 王新民，郭红丹，张德明，等.基于AHP-FUZZY的充填站位置选择[J].化工矿物与加工，2010，（10）：24-27.

WANG Xin-min，GUO Hong-dan，ZHANG De-ming，et al.The choice of filling station's location based on AHP-FUZZY[J]. Industrial Minerals&Processing，2010，（10）：24-27.

[9] 黄贯虹，方 刚.系统工程方法与应用[M].暨南大学出版社，2005.

[10]许树柏.层次分析法原理[M].天津大学出版社，1988.

[11]韩 利，梅 强，陆玉梅，等.AHP-模糊综合评价方法的分析与研究[J].中国安全科学学报，2004，（7）：86-89.

HAN Li，MEI Qiang，LU Yu-mei，et al.Analysis and study on AHP-Fuzzy comprehensive evaluation[J].China Safety Science Journal，2004，（7）：86-89.

[12]龚声武，蔡明悦，李夕兵.AHP-FCE法在采矿方法优选中的应用[J].采矿与安全工程学报，2009，（1）：41-44.

GONG Sheng-wu，CAI Ming-yue，LI Xi-bing.Application of AHP-FCE in optimizing mining method[J].Journal of Mining& Safety Engineering，2009，（1）：41-44.

[13] LIU W J，LI Y M.Optimal adaptive fuzzy control for a class of nonlinear systems[C]//2003 International Conference on Machine Learning and Cybernetics.Xi'an：Machine Learning and Cybermetics，2003，（1）：628-632.

[14] LEE H，TOMIZUKA M.Robust adaptive control using a universal approximation for SISO nonlinear systems[J].IEEE Transaction on Fuzzy Systems，2000，8（1）：95-107.

[15]姚 香．采矿方法研究与数学优选[J]．黄金，1997，（2）：15-20．

YAO Xiang．Study of mining method and mathematic optimization [J]．Gold，1997，（2）：15-20．

Optimization of Concentration Device Based on AHP-FCE

JIANG Ke1,2,3,YAO Zhong-liang1,2,3
(1.Changsha Institute of Mining ResearchCo.,Ltd.,Changsha 410012,Hunan,China；2.National Engineering Research Center for Mental,Changsha 410012, Hunan,China；3.State Key Laboratory of safety Technology of Metal Mines Mining，Changsha 410012,Hunan,China)

The stability of discharged sand pulp concentration,as the core index of filling system's normal operation, restricts the quality of filling body.Therefore,it is particularly important to select a device for tailings' concentration and storage.However,the close association with various qualitative elements of the optimization process fails to draw accurate conclusions with the conventional method.The theory of fuzzy mathematics can be applied to address this problem.The weight of the influence factors matrix was obtained according to the AHP method.The synthetic superior degree of each alternative was then worked out through FCE method.A tungsten mine in Jiangxi was used as the subject,the synthetic superior degrees of programs I,II and III were 70.5%,72.2%and 74.8%respectively according to the site conditions.The result shows that AHP-FCE method can effectively solve the tailings' concentration storage device of metal mine.

sand tank type;analytic hierarchy process;fuzzy comprehensive evaluation;weight vector

TD853.34

A

10.3969/j.issn.1009－0622.2015.06.002

2015-09-22

“十二五”科技支撑计划：金属矿床高效地下开采关键技术研究及示范项目（2013BAB02B04）

江 科（1992-），男，湖北天门人，硕士研究生，主要从事矿山充填工艺研究。

姚中亮（1960-），男，湖南望城人，教授级高级工程师，主要从事金属矿山充填工艺研究。