考虑瞬态温度场的水平井水力冲砂临界排量
2015-01-07刘清友汪兴明
刘清友, 汪兴明, 徐 涛
考虑瞬态温度场的水平井水力冲砂临界排量
刘清友1, 汪兴明2, 徐 涛2
(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;2.西南石油大学研究生院,四川成都610500)
针对目前油气田水平井水力冲砂施工难度大、难以辨识合理的冲砂排量的问题.基于水平井地层-井筒瞬时温度场模型,提出水平井环空临界流速计算模型,考虑瞬时温度场对冲砂液黏度的影响.通过有限体积法求解瞬时温度场,结合冲砂液温度-黏度方程,求取了水平井全井段全过程环空临界流速,在此基础上建立了临界排量计算新方法.通过对4种常用冲砂液进行实例分析表明:与不考虑温度情况相比,考虑温度时全过程最大环空临界流速分别增大了9.20%、17.26%、9.85%和7.64%,临界排量分别增大了8.33%、18.18%、10.00%和11.11%,说明了水平井水力冲砂排量计算考虑温度影响的必要性.
水平井;颗粒运移;临界流速;力学模型;井筒温度;瞬态热传导模型
排量是水平井水力冲砂安全高效施工的重要参数,黏度是冲砂液能否高效携带砂粒的重要性质.冲砂液和其他井下工作液在不同温度条件下,物性参数会发生变化[1].一般情况,升温后的冲砂液黏度会下降,携带砂粒的能力也会随之降低[2].
目前,进行水平井水力冲砂计算时,没有考虑温度场对冲砂排量的影响,导致计算得到的临界排量往往不能满足实际施工的需要.同时,井筒传热研究主要集中在直井或者钻井作业过程中,针对冲砂洗井作业和水平井的研究较少.但冲砂作业和钻井施工有着本质的区别,钻井过程中井下工作液的循时间较长,温度分布一般趋于稳定.而冲砂过程施工时间往往较短,井筒温度分布没有完全趋于稳定,所以考虑井筒瞬态温度场有着十分重要的意义.
现有文献对井筒传热研究主要分成两大类:半瞬态法和全瞬态法[3].半瞬态法认为井筒内的传热为稳态过程,地层内的传热为瞬态过程,该方法以Ramey模型作为理论基础[4].全瞬态温度场模型将井筒内和地层内的传热都视为瞬态过程[5].
水平井水力冲砂力学模型中,冲砂液黏度直接影响直井段砂粒的沉降速度.在斜井段和水平井段,砂粒运移机理不同于直井段,其主要形式为推移质、悬移质等[6-9].由于液固两相流的复杂性和随机性,计算该井段砂粒的临界环空速度存在较大的困难.无论砂粒以何种方式进行运移,其运动的主要动力都来源于冲砂液对砂粒的拖拽作用.拖拽力的大小与流体的黏性有直接的关系.文献[10]在水平井段借鉴水利学中泥沙瞬时起动速度来确定砂粒的沉降速度,但其中很多参数难以确定.文献[11]在大斜度井筒中建立砂粒的沉没度与砂粒起动临界流速的定量关系,考虑了砂粒运移和分布的随机性.
综上所述,无论在直径段、斜井段还是水平井段,冲砂液黏度对砂粒运移都有重要作用.若采用冲砂液地面的黏度进行临界排量计算,不能保证冲砂液高效安全的冲砂作业.本文在冲砂作业临界排量计算过程中,预先假设临界排量,采用数值计算方法得到井筒环空的瞬态温度场分布,再通过冲砂液物性方程求取冲砂液黏度,运用砂粒运移水力模型获取临界流速,然后,确定预先假定的临界排量是否满足冲砂要求,若不满足,增加排量,重复以上过程直至求出临界排量.采用此方法保证在冲砂作业中任意时刻、任意井深都满足砂粒运移的需求.
1 水平井水力冲砂水力耦合模型
目前,井眼清洁的研究主要集中在钻井过程[10-11,13-14],对冲砂作业过程中的井眼清洁相对较少.但二者有相同之处,可以借鉴钻井过程中的井眼清洁技术进行冲砂作业的研究.
1.1 模型建立
为研究方便,对模型进行如下假设:管柱的偏心和井筒中的砂粒不会对温度场产生影响.管柱和环空内的冲砂液为一维瞬态流动传热,地层内为二维瞬态传热.考虑了冲砂液流动的摩擦生热[5]和不可压缩流体[4]的性质,入口冲砂液的温度为地表温度.由于在斜井段,井眼的曲率较大,可忽略井眼倾斜对有限体积法中各个单元体积变化的影响.
1.2 水平井冲砂井筒传热模型
将冲砂作业地层-井筒传热过程简化为二维模型[12],如图1所示.
假设:
T1、T2、T3、T4分别为油管内、油管壁、环空内、套管壁的温度,K;
ρ1、ρ2、ρ3、ρ4分别为油管内流体、油管壁、环空内流体、套管壁介质的密度,kg/m3;
v1、v3分别为管柱内、环空内冲砂液的速度,m/s;
cp1、cp2、cp3、cp4分别为冲砂液、油管壁、冲砂液、生产套管壁和近井壁传热介质的比热容,J/(kg·K);
hc1、hc2、hc3分别为油管内壁、油管外壁和生产套管内壁的对流换热系数,W/(m2·K);
˙q1、˙q3分别为冲砂液油管内表面摩擦热、冲砂液与井壁和油管外表面摩擦热,W;
r1、r2、r3分别为油管内半径、外半径、生产套管内半径,m;
rx为半径,4≤x≤18,x=4时为生产套管,x=5时为水泥环,x=6时为地层或中间套管,x=7时为地层或水泥环,x=8时为地层或表层套管,x=9时为地层或水泥环,x≥10为地层;
λ2、λx分别为油管壁和近井壁介质的导热系数,W/(m·K).
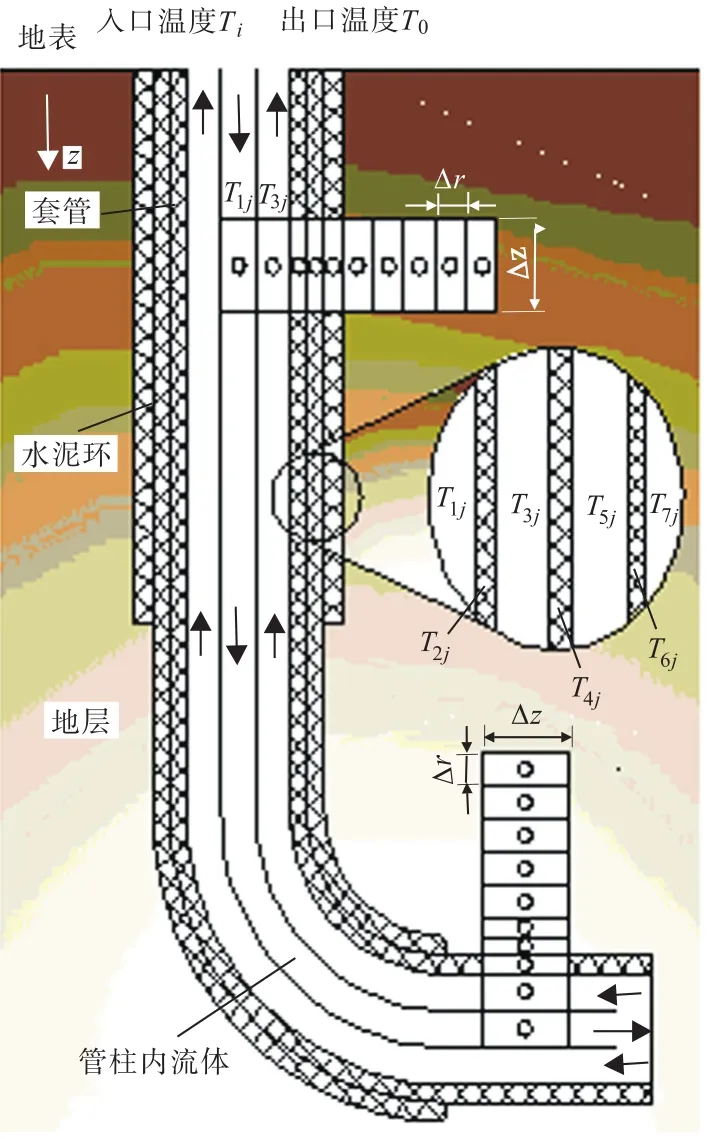
图1 水平井冲砂示意图及传热模型单元划分Fig.1 Schematic diagram of horizontal well sand washing and meshing of the heat transfer model
运用能量守恒定律,得到冲砂管柱内流体传热模型控制方程:

根据能量守恒定律,得到冲砂管柱壁传热模型控制方程:
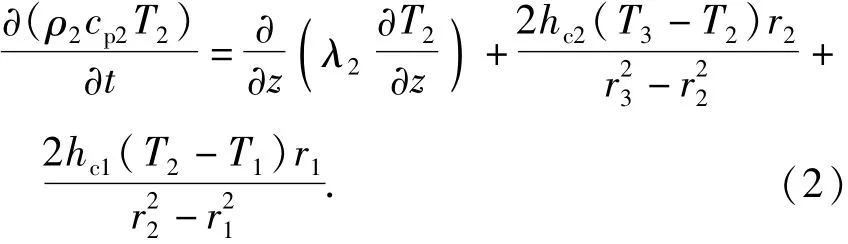
根据能量守恒方程,环空内流体传热模型控制方程:?
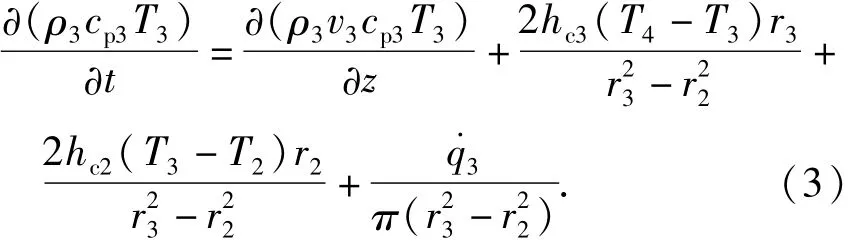
根据能量守恒原理,生产套管传热模型控制方程:
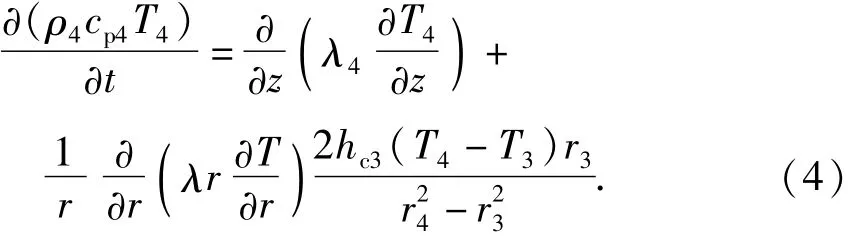
根据能量守恒定律,近井壁面传热模型控制方程:
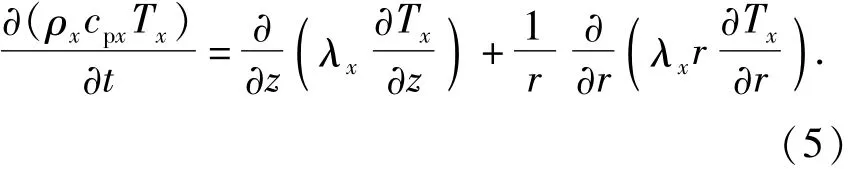
1.3 水平井冲砂水力模型
假设冲砂液为一维不可压缩流体,由连续方程可知,在环空和管柱中,冲砂液速度的数值分别保持恒定.在直井段,采用Stokes定律计算直井段砂粒的沉降速度[2].
在斜井段和水平井段,利用达西-威斯巴哈方程计算出井筒壁面的剪切应力和摩擦速度,通过文献[15]获得井筒壁面的流速分布,采用无因次沉没度[11]表示砂粒的沉没度并视其分布为随机变量,结合岩屑运移临界环空流速力学模型和砂粒翻滚以及举升临界流速计算公式[16],最终求出临界排量.
1.4 模型初始条件及边界条件
冲砂作业开始循环时,井下流体与地层之间的传热基本稳定,假设井筒初始温度与地层原始温度相同.地层相对于井眼在尺度上可以认为无穷大,假设距离井眼中心10倍井径的地层保持地层原始温度恒定不变.
2 模型求解及验证
用本文模型求解水平井水力冲砂临界排量的计算方法流程图见图2.
图2中:
Q0为预先设定临界排量,L/s;
t0为预计冲砂作业时间,一般小于24 h,s;
Q为计算排量,L/s;
ΔT为温度场控制单元两次迭代的温度差值,K;
ε为温度收敛精度,K;
Δt为时间步长,s;
ΔQ为临界排量试算增量,L/s.
采用有限体积法离散地层-井筒传热控制方程.为了提高计算精度,对传热方程中的流动项,采用二阶迎风格式进行离散.为了提高计算效率和稳定性,应用欠松弛迭代方法,传热控制方程隐式离散格式如下:
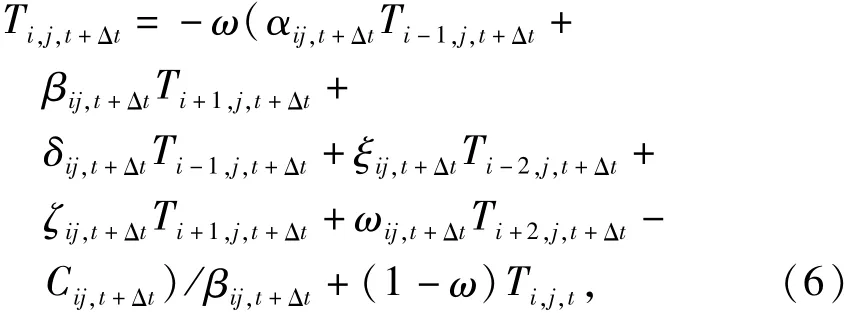
式中:
Ti,j,t+Δt为第i行第j列传热控制单元在时刻t+Δt的温度;
ω为欠松弛迭代因子,本文取ω=0.7;
α、β、δ、ξ、C均为传热控制方程隐式、二阶迎风格式离散后系数.
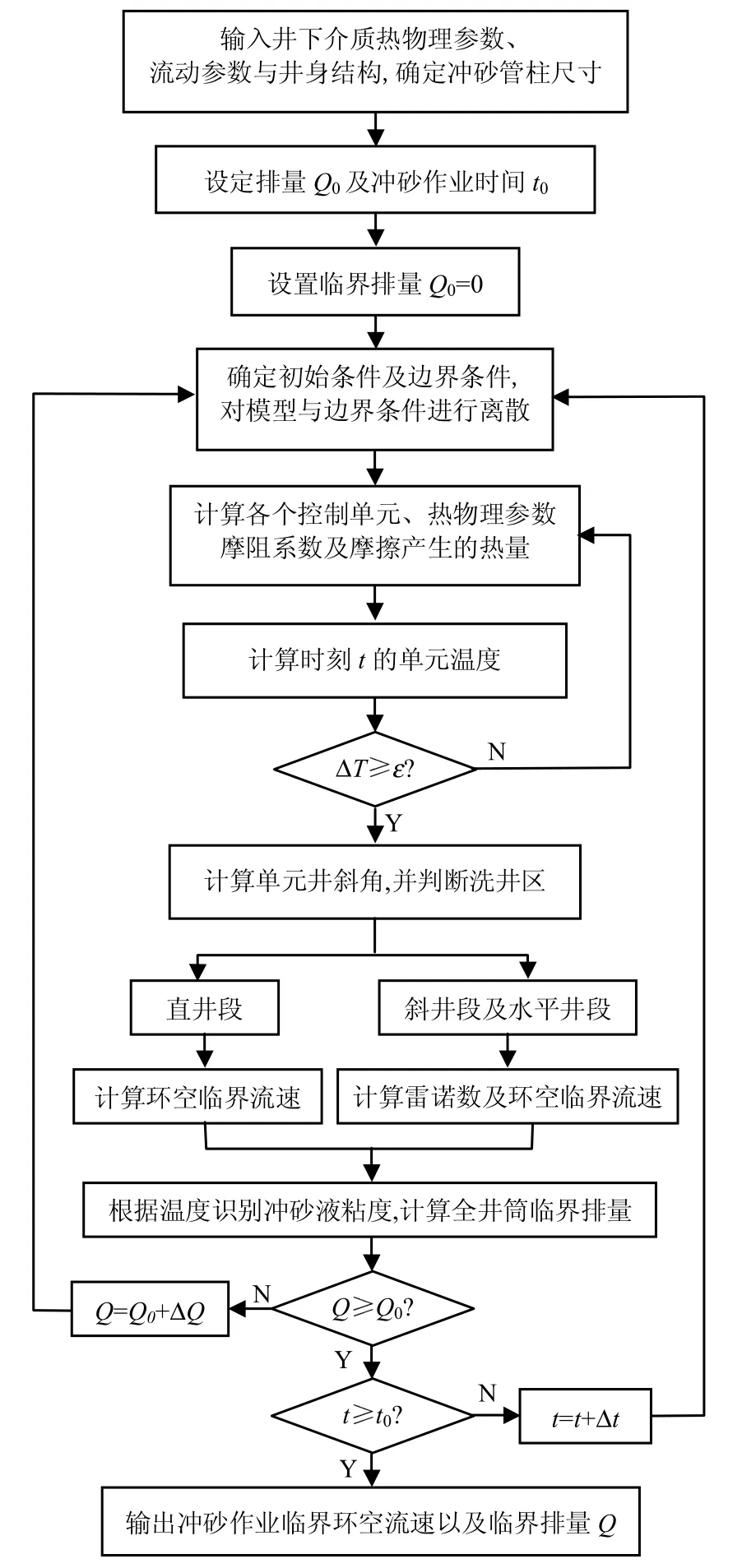
图2 模型求解步骤Fig.2 Model solution steps
表1为模拟井底温度预测结果对比.
本文模型与经典模型得到的井底温度预测结果基本一致,验证了本文瞬态温度模型的有效性.
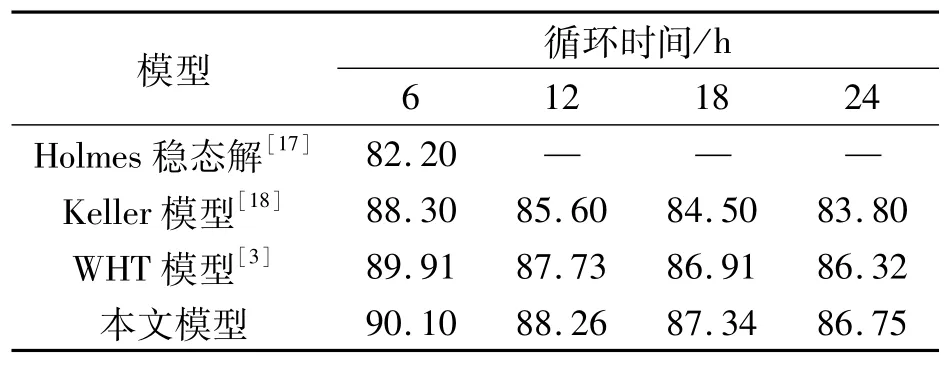
表1 模拟井底温度预测结果对比Tab.1 Comparison of simulated downhole temperature by different models℃
3 结果及讨论
3.1 算例基本参数
水平井表层套管外径为244.5 mm,下入深度为1 500 m,技术套管外径为177.8 mm,下入深度为3 000 m,生产套管外径为139.7 mm,下入深度为4 500 m.将井身结构简化为直井段-圆弧-水平段,造斜点井深为3 000 m,井斜角为0°,曲率半径为636.62 m,4 000 m井深处造斜结束,井斜角90°.一开使用直径311.15 mm的钻头,二开使用215.9 mm的钻头,三开使用165.1 mm的钻头.冲砂作业过程中,使用63.5 mm的油管.地温梯度为0.03℃/m.其他参数如下:
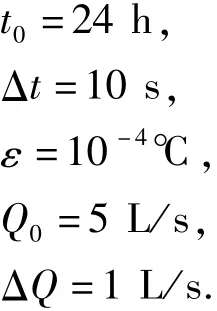
无论是油井、气井和水井,冲砂作业最普遍采用的冲砂液为清水,本文采用文献[19]的清水物性参数.在模型分析过程中,其他冲砂液的热物性参数采用文献[3]的数据,以及文献[20]给出的常用井下工作液黏度-温度的数学模型.
3.2 计算结果分析
应用本文编制程序,在考虑瞬态温度变化和未考虑瞬态温度变化两种情况下,得到4种类型冲砂液水平井水力冲砂环空临界排量.考虑温度场影响的临界排量分别为13、13、11和10 L/s,不考虑温度影响的临界排量分别为12、11、10和9 L/s,偏差分别为8.33%、18.18%、10.00%和11.11%.
表2为在井深3 000 m处考虑温度影响与未考虑温度影响的临界环空流速的相对偏差.由表2可知,温度变化对环空临界流速的影响也很显著.
表3为斜井段和水平井段,考虑温度影响与未考虑温度影响的最大临界环空流速相对偏差.
由表3可知,在斜井段及水平井段,温度变化对冲砂排量的影响也是明显的.

表2 井深3 000 m临界流速偏差对比Tab.2 Comparison of the critical flow rate deviation at 3 000 m depth in the horizontal well
图3为考虑温度影响时,在环空临界排量的情况下的黏度变化曲线,以及不同循环时间(0、1、3、6、12和24 h)的环空流体温度变化曲线.
由图3可知,在循环期间,4种冲砂液的环空温度和黏度不断变化,开始循环时温度变化较大,随后逐渐稳定.环空中冲砂液开始温度较高,黏度较小,随后随着温度的降低,黏度增大.
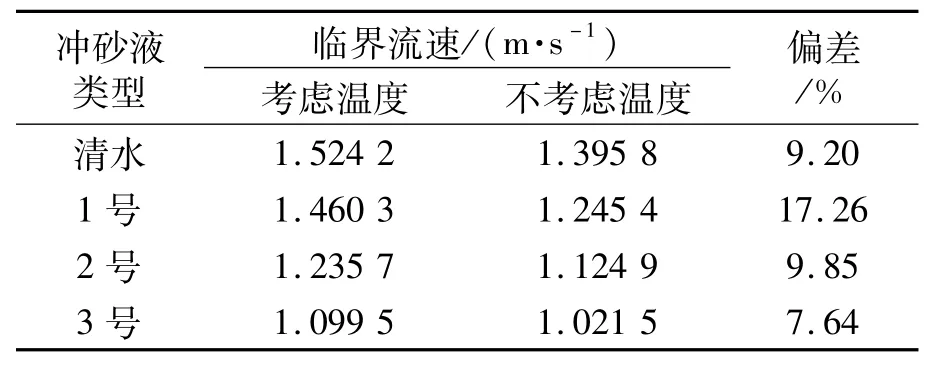
表3 斜井段及水平井段临界流速偏差对比Tab.3 Comparison of the critical velocity deviation in the inclined and the horizontal sections
图4为冲砂作业期间直井段环空临界流速的变化范围,以及4种冲砂液不考虑温度影响的临界环空流速.图5为斜井段及水平井段临界流速变化.
在斜井段和水平井段,砂粒的运移机理不同于直井段,影响砂粒运移的因素不仅与黏度有关,还与砂粒沉没度、砂粒直径等因素有关[11],所以,临界环空流速的变化幅度较小.斜井段是砂粒最难运移的区域,其最终决定水力冲砂临界排量的大小.

图3 不同冲砂液环空温度及黏度变化Fig.3 Variation of the annulus fluid temperature and viscosity for different SCFs
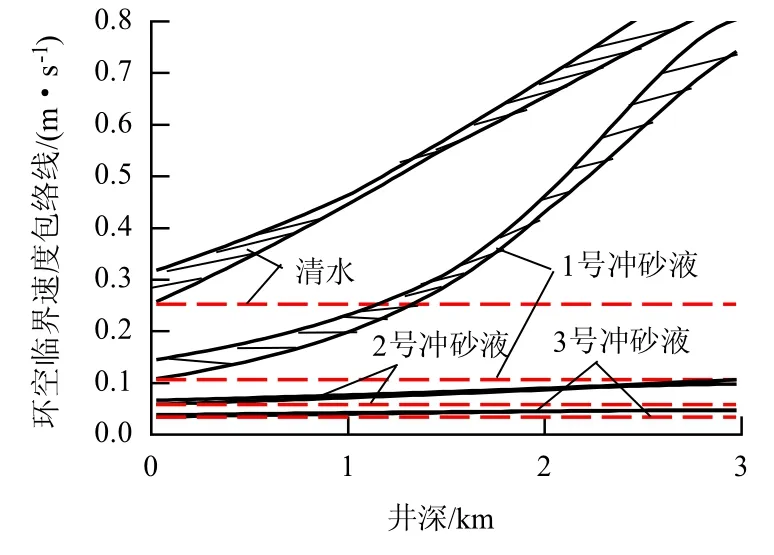
图4 直井段临界流速变化Fig.4 Variation of the critical velocity in the vertical section
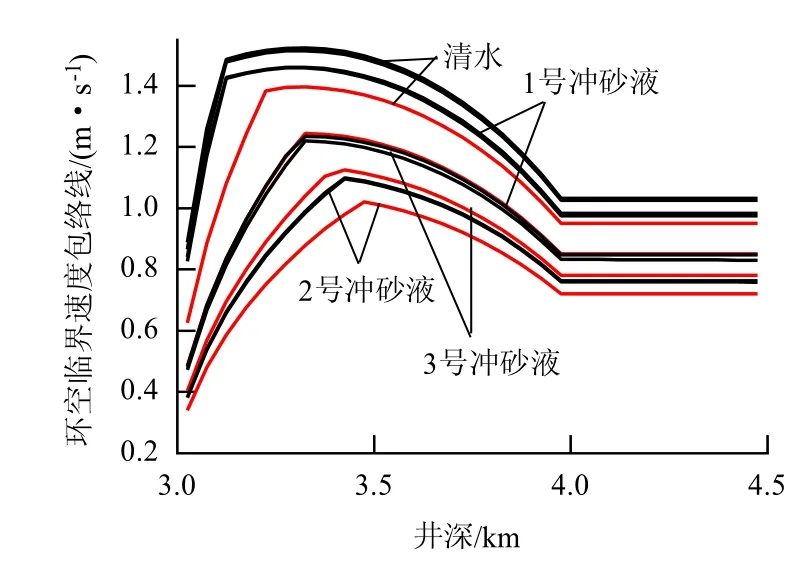
图5 斜井段及水平井段临界流速变化Fig.5 Variation of the critical velocity in the inclined and the horizontal sections
4 结束语
本文建立了水平井全井段水力冲砂临界排量计算与水平井水力冲砂瞬态温度场的耦合模型,在此基础上,采用有限体积法求解水平井水力冲砂瞬态温度场模型,结合现场常用的冲砂液物性方程,分析了瞬时温度场度对水平井水力冲砂排量的影响.
经分析得知,直井段砂粒运移的临界环空流速主要取决于冲砂液的黏滞阻力,所以,冲砂液黏度变化对砂粒运移有重要影响.冲砂液黏度随温度变化较大,保障砂粒运移的临界环空流速也会发生显著变化.所以,在直井段考虑瞬时温度场的影响是十分必要的.
在斜井段,砂粒运移最为困难,影响砂粒运移的因素不仅包括冲砂液对砂粒的拖拽作用,还与砂粒直径、砂粒沉没度等因素有关.所以,冲砂液黏度变化对砂粒的运移影响相对于直井段较弱.本文计算分析可知,若不考虑温度影响,斜井段以及水平井段的环空临界流速与实际工况要求存在较大偏差.综合以上分析,结合本文提出的计算方法及分析结果,为了保证水平井水力冲砂,以及钻井作业高效、快速、安全地施工,考虑瞬时温度场度对井下工作液携岩作用的影响有十分重要的意义.
[1] 管志川,李千登,宁立伟,等.钻井液热物性参数测量及其对井筒温度场的影响[J].钻井液与完井液,2011,28(3):1-4.GUAN Zhichuan,LI Qiandeng,NING Liwei,et al.Study on drilling fluid thermal properties measurement and influence on wellbore temperature field[J].Drilling Fluid and Completion Fluid,2011,28(3):1-4.
[2] 刘希胜.钻井工艺原理:中钻进技术[M].北京:石油工业出版社,1988:31.
[3] 宋洵成,管志川.深水钻井井筒全瞬态传热特征[J].石油学报,2011,32(4):704-708.SONG Xuncheng,GUAN Zhichuan.Full transient analysis of heat transfer during drilling fluid circulation in deep-water wells[J].Acta Petrolei Sinica,2011,32(4):704-708.
[4] RAMEY H J.Wellbore heat transmission[J].Journal of Petroleum Technology,1962,14(4):427-435.
[5] RAYMONDLR.Temperaturedistributionina circulating drillingfluid[J].JournalofPetroleum Technology,1969,21(3):333-341.
[6] 李洪乾,杲传良,任耀秀,等.水平井钻井第二洗井区环空止动返速的计算[J].石钻探技术,1995(增刊):27-29,85.LI Hongqian,GAO Chuanliang,REN Yaoxiu,et al.Calculation of annular slip velocity in the 2nd cleaning duringhorizontaldrilling[J].PetroleumDrilling Techniques,1995(Sup.):27-29,85.
[7] 沈燕来,陈建武.冲砂洗井水力计算方法综述[J].水动力研究与进展,1998,13(3):347-353.SHEN Yanlai,CHEN Jianwu.Brief review on hydraulic calculation methods of sand flushing[J].Journal of Hydrodynamics,1998,13(3):347-353.
[8] 李洪乾,刘希圣.水平井岩屑床止动模型的建立[J].石油大学学报:自然科学版,1994,18(2):33-38.LI Hongqian,LIU Xisheng.Establishment of unslided cuttings bed model in horizontal well drilling[J].Journal of the University of Petroleum:Natural Science,1994,18(2):33-38.
[9] 汪志明,张政.大位移水平井两层不稳定岩屑传输模型研究[J].水动力研究与进展,2004,19(5):676-681.WANG Zhiming,ZHANG Zheng.A two-layer timedependent model for cuttings transport in extended-reach horizontal wells[J].Journal of Hydrodynamics,2004,19(5):676-681.
[10] 曲洪娜,黄中伟,李根生,等.水平井旋转射流冲砂洗井水力参数设计方法[J].石油钻探技术,2011,39(6):39-43.QU Hongna,HUANG Zhongwei,LI Gensheng,et al.Hydraulic parameters of sand-flushing with rotating jets in horizontal wells[J].Petroleum Drilling Techniques,2011,39(6):39-43.
[11] 董长银,邓珊,李爱萍,等.大斜度井筒条件下沉积砂床表面颗粒起动临界条件研究[J].石油钻探技术,2010,38(3):22-28.DONG Changyin,DENG Shan,LI Aiping,et al.Research of critical condition for grains at bed surface inhighlydeviatedwells[J].PetroleumDrilling Techniques,38(3):22-28.
[12] 杨谋,孟英峰,李皋,等.钻井全过程井筒-地层瞬态传热模型[J].石油学报,2013,34(2):366-371.YANG Mou,MENG Yingfeng,LI Gao,et al.A Transient heat transfer model of wellbore and formation during the whole drilling process[J].Acta Petrolei Sinica,2013,34(2):366-371.
[13] 汪海阁,刘希圣,丁岗,等.水平井段岩屑床厚度模式的建立[J].石油大学学报,自然科学版,1993,17(3):25-32.WANG Haige,LIU Xisheng,DING Gang,et al.The model of cuttings bed thickness in horizontal well section[J].Journal of the University of Petroleum, China,1993,17(3):25-32.
[14] 周风山,蒲春生.水平井偏心环空中岩屑床厚度预测研究[J].石油钻探技术,1998,26(4):17-19,60.ZHOUFengshan,PUChunsheng.Studyon predication of cuttings bed thickness in eccentric annular inhorizontalwell[J].PetroleumDrilling Techniques,1998,26(4):17-19,60.
[15] 张兆顺.流体力学[M].北京:清华大学出版社,2006:338-340.
[16] CLARK R K,BICKNAM K L.A mechanistic model for cuttings transport[C]∥SPE Annual Technical Conference and Exhibition.New Orleans:Society of Petroleum Engineers,1994:139-153.
[17] CHARLES S,SAMMUEL H,SWIFT C.Calculations ofcirculatingmudtemperatures[J].Journalof Petroleum Technology,1970,22(6):670-674.
[18] KELLER HH,COUCHEJ,BERRYPM.Temperaturedistributionincirculatingmud columns[J].SPE Journal,1973,13(1):23-30.
[19] POPIEL C O,WOJTKOWIAK J.Simple formulas for thermophysical properties of liquid water for heat transfer calculation(from 0℃to 150℃)[J].Heat Transfer Engineering,1998:19(3),87-101.
[20] SANTOYA E,SANTOYA-GUTIERREZ S,GARCIA A,et al.Rheological property measurement of drilling fluids used in geothermal wells[J].Applied Thermal Engineering,2001,21:283-302.
(中文编辑:秦萍玲 英文编辑:兰俊思)
Critical Discharge Flow of Sand Cleaning Fluid Considering Transient Temperature Effect of Horizontal Well
LIU Qingyou1, WANG Xingming2, XU Tao2
(1.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China;2.Graduate School of Southwest Petroleum University,Chengdu 610500,China)
Hydraulic sand cleaning operation of horizontal well in oil and gas fields is difficult because it is hard to obtain a reasonable discharge volumetric flow of the sand cleaning fluid(SCF)in practice.To solve this problem,an annular critical velocity model that is based on the transient thermal model of formation and wellbore during sand cleaning operation was proposed to recognize the SCF critical velocity in horizontal well.Taking into account the influence of transient temperature field on the SCF viscosity,the finite volume method(FVM)was used to obtain the transient thermal distribution,and the transient annulus critical velocity of the whole wellbore was calculated by solving the temperature-viscosity equation of the SCF.On this basis,a new method for calculating the critical discharge flow of SCF was then developed.As a case study,the critical velocities of four typical SCFs were calculated using the proposed method.The results show that the critical velocities of the four SCFs when considering the effect of temperature are 9.20%,17.26%,9.85%,and 7.64% respectively lager than that without considering the thermal effect;and the critical discharge flow are 8.33%,18.18%,10.00%,and 11.11%larger respectively.Therefore,temperature should be considered to optimize the critical velocity and discharge flow of SCFs in horizontal well.
horizontal well;particles transportation;critical velocity;mechanics model;wellbore temperature;transient heat transfer model
TE252
A
0258-2724(2014)06-1123-07
10.3969/j.issn.0258-2724.2014.06.028
2014-03-10
国家自然科学基金重点资助项目(51134004)
刘清友(1965-),男,教授,博士生导师,长江学者特聘教授,研究方向为石油机械、油气井管柱力学、岩石破碎与钻头及计算机仿真等,E-mail:liuqy66@aliyun.com
刘清友,汪兴明,徐涛.考虑瞬态温度场的水平井水力冲砂临界排量[J].西南交通大学学报,2014,49(6):1123-1129.
