基于α-邻近的改进蚁群算法
2015-01-06吕金秋游晓明
吕金秋,游晓明,刘 升
(上海工程技术大学a.电子电气工程学院;b.管理学院,上海201620)
基于α-邻近的改进蚁群算法
吕金秋a,游晓明a,刘 升b
(上海工程技术大学a.电子电气工程学院;b.管理学院,上海201620)
为克服传统蚁群系统(ACS)在较大规模问题计算中易陷入局部最优,以及求解精度较低等不足,提出一种新的改进蚁群算法。该算法引入最小1-树中的α-邻近概念,能更好地反映给定边属于最优回路的概率,通过转换邻接矩阵,计算出最优回路的下界,以此提高α值的精度,并给出适应性探索策略,加入3-opt领域搜索算子,有效提高优化解的精度。实验结果表明,该算法具有更好的全局寻优能力,与ACS等算法相比能获得更加优化的解。
蚁群系统;α-邻近;最小1-树;下界;适应性策略;旅行商问题
1 概述
旅行商问题(Traveling Salesman Problem, TSP)[1]是组合优化问题领域中研究和关注次数最多的问题之一,其可以描述成在一张带权完全无向图中,寻找一条具有最小权值的汉密尔顿回路。蚁群优化(Ant Colony Optimization,ACO)算法[2]作为一种新型的智能群体协作算法,可以直接应用到TSP中。尽管第一个ACO算法(蚂蚁系统(Ant System,AS))得到的优化结果逊于其他TSP经典算法,但它为一系列扩展算法的出现提供了灵感。这些扩展的算法具有分布式计算、自学习、鲁棒性强和易与其他算法相结合的优点[3],已广泛应用于调度问题、分配问题、图像处理等诸多领域。
此外,大量学者针对蚁群算法及其应用展开了研究。比如,文献[4]提出了多种群的概念,利用不同群落搜索解空间,从而极大程度上避免了算法陷入局部最优解;文献[5]提出了基于超顶点交流策略的并行蚁群算法,通过减少各种群的之间的通信量提高了算法效率;文献[6]采用双重最邻近插入法(dual nearest insertion)初始化信息素,利用最优解的下界强化学习,并结合了L-K邻域搜索算法;文献[7]提出量子蚁群算法,即采用量子比特的概率幅表示蚂蚁的当前位置,采用量子旋转门更新蚂蚁的位置,从而使搜索空间加倍,算法的精确度和鲁棒性得以增强;文献[8]定义一种新的方向信息素来刻画寻优过程中的全局信息,从而可以较好地克服算法停滞现象,并在最优路径的基础上提高了解的全局性。
本文将α-邻近的思想引入到启发函数ηij的计算中,得出一种新的启发函数计算公式,该启发函数值更能反映出一条边属于最优回路的概率。随后,通过转换邻接矩阵,计算最优回路的下界,从而提高α的精度。此外,还提出了一种新的选择策略——适应性探索策略,即在进化前期通过刺激蚂蚁选择信息素较弱的路径,扩大蚁群种群多样性,在进化后期加速种群的收敛。
2 算法描述
2.1 算法框架
本文算法(α-AACS)的框架以伪代码的形式给出,如下:
输入TSP测试数据
输出遍历路径

2.2 基于最小1-树的启发函数
在原始的蚁群系统(Ant Colony System,ACS)中,位于城市i的蚂蚁个体k根据伪随机比例规则选择下一个访问的城市j。具体如下[2]:
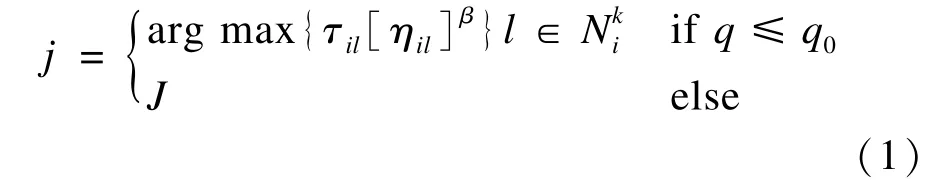
其中,q是均匀分布在区间[0,1]中的一个随机变量,q0(0≤q0≤1)是一个参数;J是根据下式给出的概率分布产生出来的一个随机变量(α=1):

其中,ηij=1/dij为启发函数;α为信息启发式因子;β为期望启发式因子;代表了位于城市i的蚂蚁个体k可以继续访问的城市的集合,即所有未被蚂蚁k访问的城市集合。
此转移规则在一定程度上阻碍算法搜索到最优路径。假设一条边不属于其2个顶点的最近的邻近边集,而却属于最优回路的边集,这种情况下算法就很难寻得最优解。因此,本文引入了α-nearest[9]的概念,它可以更好反映一条边属于最优回路的概率。
定义1设图G=(N,E),则其1-树是指在图G′=(N{1},E)(1为图G的第一个顶点)的生成树中加入2条与点1相连的边所生成的图形。那么,图G的最小1-树就是边长总和最小的1-树。
定义2设最小1-树T的长度为L(T),T+(i,j)为包含边(i,j)的最小1-树的长度,则边(i,j)的α值由下式求得:
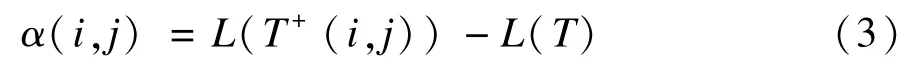
设β(i,j)为在最小1-树中加入边(i,j)时去除的边的长度,则α(i,j)=c(i,j)-β(i,j),其中,c(i,j)表示边(i,j)的欧式距离。如图1所示,若(j1,j2)是最小1-树的一条边,i是最小1-树中的一点(i≠j1,j2)。增加边(i,j2)后会产生一个闭合回路,点j1位于此回路上,那么β(i,j2)即为β(i,j1)和c(j1,j2)中的最大值。

图1 β(i,j2)计算结构
设b和mark为2个一位数组,其中,b[j]=β(i,j),数组mark用来表示b[j]已针对点i计算并被赋值。数组b[j]的计算分为2步:首先计算从节点i到最小1-树的根节点的路径上的所有点的b值,这些点的mark[j]=i;然后再向前计算剩下所有点的b值。随后,α值的计算将在内循环中进行。本文计算α值的伪代码如下:

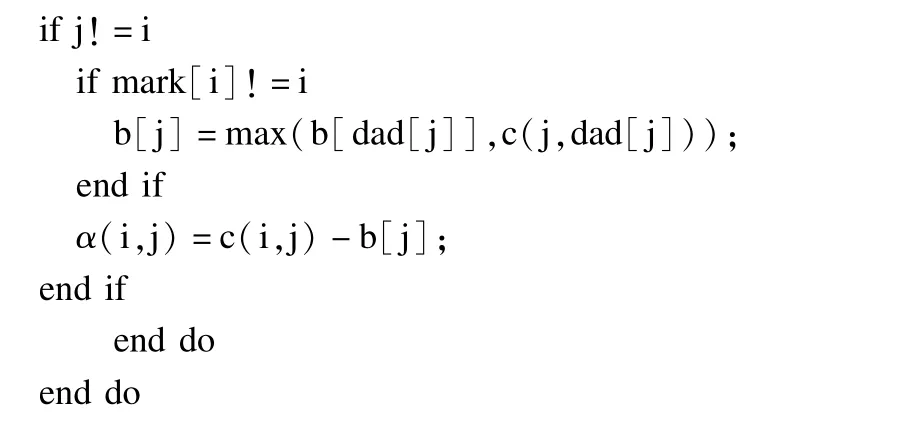
下面给出了新的基于α-邻近的启发函数的计算步骤。这里,φ为一正常量参数。
步骤1用Prim算法[10]计算图G′=(N{1},E)的最小生成树;
步骤2在最小生成树中加入2条与点1相连的最短边,即得图G的最小1-树;
步骤3计算每条边的α(i,j)值;
步骤4ηij=1/[α(i,j)+φ]。
2.3 下界计算
在2.2节中,α值较理想的估算了一条边属于最优回路的概率。实验结果表明一条边的α值比其长度更能代表其属于最优回路的可能性。然而,α值的精度可以通过对原始的邻接矩阵做一个简单的转换而大大提高。转换公式如下:

其中,向量π=(π1,π2,…,πn)。当邻接矩阵C= (cij)转换到新的矩阵D=(dij)的时,D的最优回路同时也是C的最优回路,只是长度增加了2∑πi。设Tπ为D的最小1-树,那么其长度L(Tπ)即是D的最优回路长度的下界,同时,w(π)=L(Tπ-2∑πi也就是C的最优回路长度的下界,即要找到一个向量π=(π1,π2,…,πn)使得下界w(π)最大。当w(π)>w(0)时,从D求得的α值比从C求得的α值能更好地反映一条边属于最优回路的可能性。
本文使用次梯度优化(subgradient optimization)迭代法[11]来求w(π)最大值。迭代公式为πk+1=πk+tk(0.7vk+0.3vk-1),其中,vk为次梯度向量(v-1=v0);tk为步长(正数)。次梯度向量计算式为vk=dk-2,其中,向量dk中的元素为当前最小1-树中每个节点的度。此迭代法使得最小1-树中节点的度逐渐变为2,即形成一回路。下面给出了次梯度优化的步骤:
步骤1设k=0,π0=0,W=-∞。
步骤2求最小一树Tkπ。

步骤4则W=max(W,w(πk))。
步骤5计算vk=dk-2,其中,向量dk的元素是中节点的度。
步骤6 如果vk=0(即为最优回路),或者满足终止条件,则算法结束;否则,进入下一步。
步骤7 更新步长tk+1=2tk,直到W不在增长, (t0=1)。
步骤8计算:
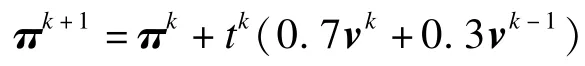
其中,v-1=v0。
步骤9k=k+1返回到步骤2。
文献[12]已经证明,当tk→0(k→0),∑tk=∞时,W总会收敛到w(π)的最大值。
2.4 适应性探索策略
在式(1)中,参数q0决定着蚁群是选择当前可能的最优移动方式还是探索其他路径。换言之,通过调整q0可以调节算法对新路径的探索度,从而决定蚁群是应该集中搜索至今最优路径附近的区域,还是应该探索其他区域。因此,本文的适应性探索策略是指在进化前期设定较小的q0值来增加种群多样性,在进化后期设定较大的q0值以加速算法收敛。
2.5 3-opt邻域搜索
3-opt邻域搜索是指在原回路的基础上改变最多3条边得到的长度更短的新的回路。本文使用α值设定候选集,即α值越小,则这条边在候选集的排名越靠前,并且候选集长度设为5。表1给出了532个城市分别用距离成本c值、α值和改进过后的α值作为候选集设定标准时,最优回路中的边在各自候选集中的排名比例[9]。3种情况的平均排名分别为2.4%,2.1%,1.7%。显然,采用改进后的α值,平均排名比例明显提高。
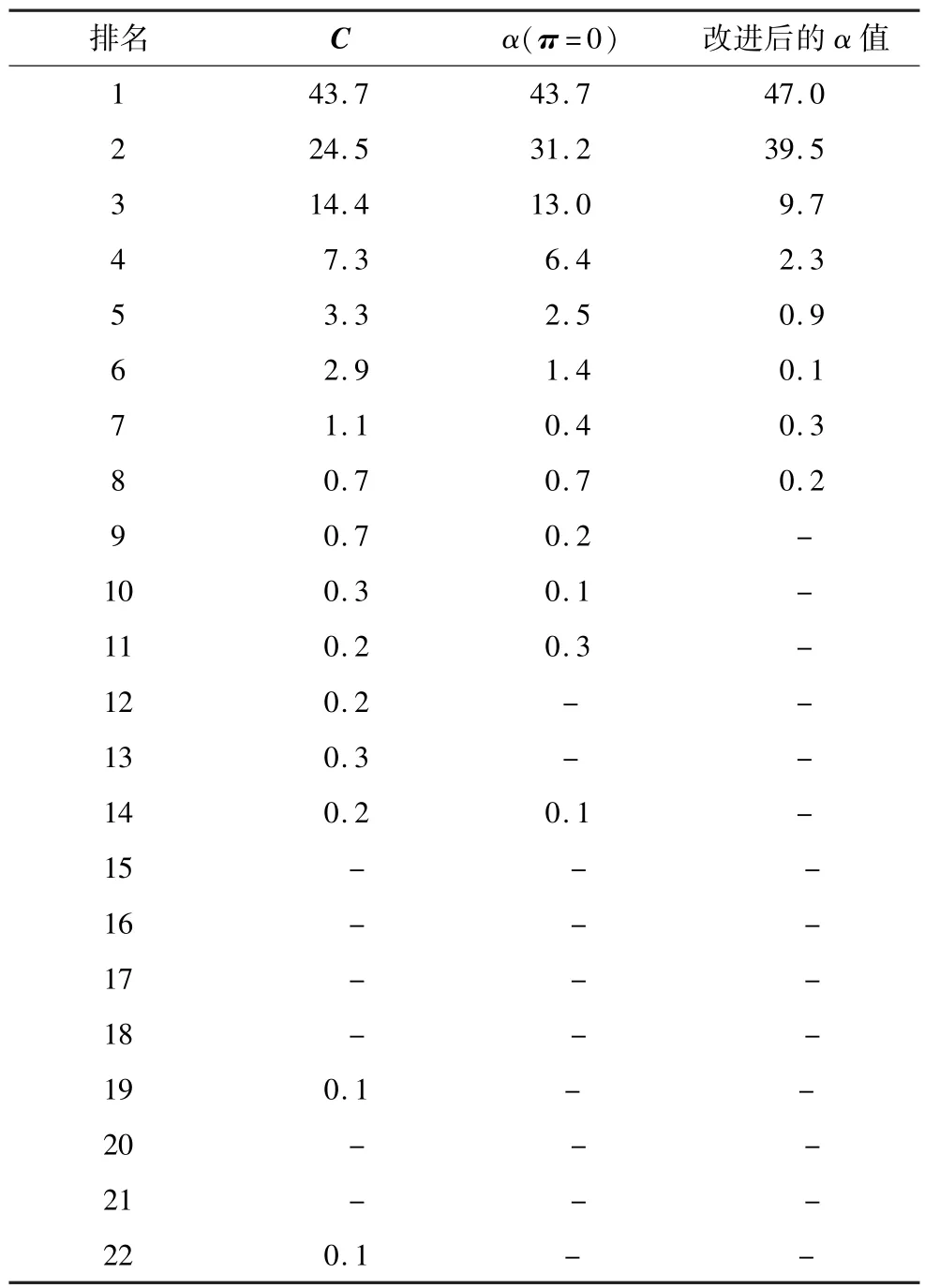
表1 TSP各最优边在候选集中的排名比例%
在原回路上去掉3条边得到3个子路径,有4种方式可以将这3个子路径重新组合成回路,如图2所示。

图2 4种3-opt交换方式
2.6 算法复杂度分析
由文献[13]可知,原ACS算法的时间复杂度为T(n)=O(Nc·n2·m),其中,n为TSP的规模;m为蚂蚁数目;Nc为最大迭代次数。本文算法中计算α值算法的时间复杂度为O(n2),3-opt邻域搜索的时间复杂度为O(n3),故本文算法的时间复杂度为T(n)=O(Nc·n2·m)+O(Nc·n3)。由此可见,在TSP的规模n和蚂蚁数目m相等的情况下,本文算法时间复杂度没有增加。
3 实验结果与分析
为证明本文算法的有效性,本节利用标准测试集TSPLIB[14]中的实例进行了大量的实验,并与其他算法的实验结果进行了比较。对每一个测试实例和每一种算法进行10次实验。
表2针对6种不同的测试实例,比较了本文算法(α-AACS)、ACS+3opt和ACS的实验结果。由表2可知,在Eil51和Kroa150问题中,本文算均能获得最优解;在Kroa100、Kroa200和Pr264问题中,本文算法均能获得与已知最优解极其相近的解,误差可近似为0;在大规模问题Lin318中,本文算法所求解的误差为0.37%,比ACS算法缩小了约7%。由此可见,α-AACS的性能胜于其他2种算法,并且能获得最优解或接近最优解。

表2 3种算法实验结果对比
图3给出针对Kroa150测试实例[14]3种算法的收敛曲线,其中,路径长度为虚值无单位。

图3 3种算法关于Kroa150测试实例的收敛曲线
表3比较了在本文算法中采用不同q0值,并应用到不同的测试实例中得到的回路的平均长度(虚值)。可以看出,本文算法采用第3组q0时在3个测试问题中所获解的平均长度均优于前2组解的平均长度。
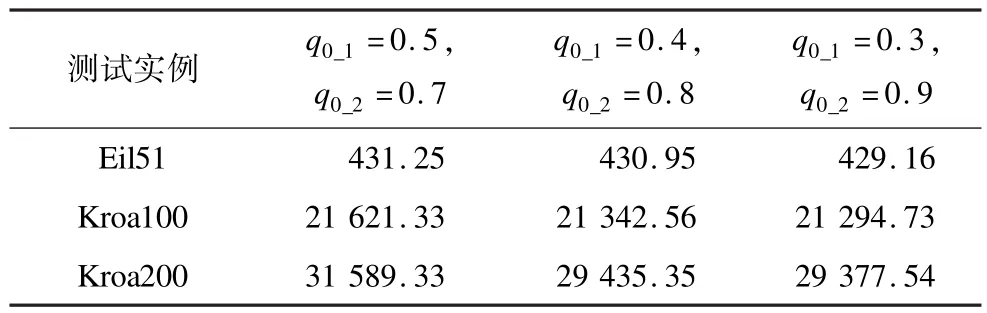
表3 本文算法不同条件下回路的平均长度对比
由此可见,当q0_1=0.3,q0_2=0.9,算法能够获得更好的结果,并且在寻优过程中具有较好的稳定性。图4是针对Kora200测试实例采用3组参数得到的收敛曲线。由此得,本文算法中参数q0的值设定为q0_1=0.3,q0_2=0.9时所获解最佳。

图4 本文算法Kroa150测试实例下的收敛曲线
4 结束语
本文提出一种新的蚁群优化算法(α-AACS)。引入最小1-树的α-nearest用来计算启发信息值,给出通过计算最优回路的下界提高α值精度的方法。此外,适应性探索选择策略的提出和3-opt邻域搜索的加入提高了优化解的精度。实验结果表明,该算法能获得较大规模TSP问题的全局最优值或接近最优值。今后将研究一般性k-opt子交换邻域搜索,并将其应用到蚁群优化算法中。
[1] Stutzle T,Hoos H.MAX-MIN Ant System and Local Search for the Traveling Problem[C]//Proceedings of IEEEInternationalConferenceonEvolutionary Computation.Indianapolis,USA:IEEE Press,1997: 309-315.
[2] Dorigo M,Stutzle T.Ant Colony Optimization[M]. Cambridge,USA:MIT Press,2004.
[3] 金 弟,杨 博,刘 杰,等.复杂网络簇结构探测——基于随机游走的蚁群算法[J].软件学报, 2012,23(3):451-464.
[4] Chen Fa.A New Hybrid Heuristic Approach for Solving Large Traveling Salesman Problem[J].Information Sciences,2004,166(4):67-81.
[5] 章春芳.基于超顶点交流策略的并行蚁群算法[J].江南大学学报:自然科学版,2007,6(6):895-899.
[6] Zhang Ying,Li Lijie.MST Ant Colony Optimization with Lin-Kerninghan Local Search for the Traveling Salesman Problem[C]//Proceedings of International Symposium on Computational Intelligence and Design. Wuhan,China:[s.n.],2008:344-347.
[7] 李 煜,马 良.用量子蚁群算法求解大规模旅行商问题[J].上海理工大学学报,2012,34(4):355-358.
[8] 孟祥萍,片兆宇,沈中玉,等.基于方向信息素协调的蚁群算法[J].控制与决策,2013,28(5):782-786.
[9] Helsgaun K.An Effective Implementation of the Lin-Kernighan Traveling Salesman Heuristic[J].European JournalofOperationalResearch,2000,126(1): 106-130.
[10] Prim R C.Shortest Connection Networks and Some Generalizations[J].Bell System Technical Journal, 1957,36(1):1389-1401.
[11] Held M,Karp R M.The Traveling-salesman Problem and Minimum Spanning Trees:Part II[J].Mathematical Programming,1971,1(1):16-25.
[12] Poljak B T.A General Method of Solving Extremum Problems[J].Soviet Mathematics:Doklady,1967, 8(1):593-597.
[13] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.
[14] University of Heidelberg.TSPLIB Website[EB/OL]. (2013-11-21).http://www.iwr.Uni-heidelberg.de/ groups/comopt/software/TSPLIB95/tsp.
编辑 刘 冰
Improved Ant Colony Algorithm Based on α-nearest
LV Jinqiua,YOU Xiaominga,LIU Shengb
(a.College of Electronic and Electrical Engineering;b.School of Management, Shanghai University of Engineering Science,Shanghai 201620,China)
In order to overcome the disadvantages that traditional Ant Colony System(ACS)is easy to fall into local optimum and low-precision for large-scale problems,this paper presents an improved ant colony optimization algorithm. The algorithm introduces α-nearest in the minimum1-tree,which better reflects the chances of a given link being a member of an optimal tour.It improves α-nearest precision by transforming the adjacency matrix and computes a lower bound.Besides,it proposes the adaptive exploration strategy and 3-opt local search.Experimental results show that this algorithm has a better global searching ability in finding the best solutions and can obtain better solutions than ACS,etc.
Ant Colony System(ACS);α-nearest;minimum1-tree;lower bound;adaptation strategy;Travelling Salesman Problem(TSP)
吕金秋,游晓明,刘 升.基于α-邻近的改进蚁群算法[J].计算机工程,2015,41(2):184-188.
英文引用格式:Lv Jinqiu,You Xiaoming,Liu Sheng.Improved Ant Colony Algorithm Based on α-nearest[J].Computer Engineering,2015,41(2):184-188.
1000-3428(2015)02-0184-05
:A
:TP18
10.3969/j.issn.1000-3428.2015.02.035
国家自然科学基金资助项目(61075115);上海市教委科研创新基金资助重点项目(12ZZ185)。
吕金秋(1991-),男,硕士,主研方向:智能信息处理,嵌入式系统;游晓明、刘 升,教授、博士。
2014-03-12
:2014-04-10E-mail:yxm6301@163.com
