0-1规划的一种连续化和罚函数解法

祝丽华

(福建工程学院数理系，福建福州 350118)

0-1规划的一种连续化和罚函数解法

祝丽华

(福建工程学院数理系，福建福州 350118)

针对0-1规划问题变量的离散特点，提出一种连续化和罚函数解法。先通过一个非线性等式约束表示为［0，1］区间上等价的连续变量非线性规划等式，再利用罚函数法将约束问题转化为无约束问题求解。对多个算例进行计算，数值结果表明该方法是可行和有效的。

0-1规划;连续化;约束非线性规划;罚函数

0-1规划问题是变量只取0或1的整数规划问题的特殊情形，是运筹学中典型的组合优化难题。在机械、化工、计算机、经济、生物、军事、社会等各领域的许多优化问题可以归结为0-1规划问题，如最常见的背包问题、分配问题和生产与存储计划问题等。因此构造0-1规划问题的求解方法是一个具有理论意义和实用价值的研究课题。

目前求解这类问题的经典方法有分支定界法、割平面法和隐枚举法等，除此之外人们已研究出一些启发式算法，如贪婪算法，全局优化方法如遗传算法［1］、模拟退火算法［2］和蚁群算法［3］等。考虑到该类问题中变量只能取0或1这两个离散点，一般的连续算法不适用该类问题，许多学者应用不同的连续化方法先将问题转化为连续变量的规划问题然后求解，最易想到的方法是直接将变量松弛为［0，1］区间上的连续变量，然后对连续解“舍入取整”。高峰等［4］提出针对一种整系数多项式0-1整数规划问题，应用罚函数将含等式和不等式的0-1多项式规划连续化为无约束多项式规划问题。Kiwie等［5］提出通过应用求解凸规划的Bregman临近点算法来求解大规模0-1规划问题。李艳艳等［6］利用拉格朗日松弛对偶将问题转化为无约束问题，再应用凝聚函数连续化对偶问题求解。隋允康［7］等人通过一个非线性等式约束，将0-1离散规划表示为［0，1］区间上等价的连续变量非线性规划，再使用乘子法、离散约束变换法处理非线性的等式约束后，利用遗传算法GENOCOP进行求解，这些方法都是对0-1规划问题求解的有益尝试，但一般只适用于某一类0-1规划问题，在应用上有一定的局限性。

本文根据0-1规划变量的离散特点，利用一个整数变量的非线性等式约束替换原变量的整数约束，从而将原离散的0-1规划问题转化为一个变量约束在［0，1］区间上的等价连续规划问题，由于连续化后的问题是约束非线性问题，求解比较困难，本文利用罚函数［8］将约束吸收到目标函数，再应用牛顿法求解。算例的数值结果表明该方法是有效的、可行的。

1 0-1规划的连续化

考虑如下0-1规划问题

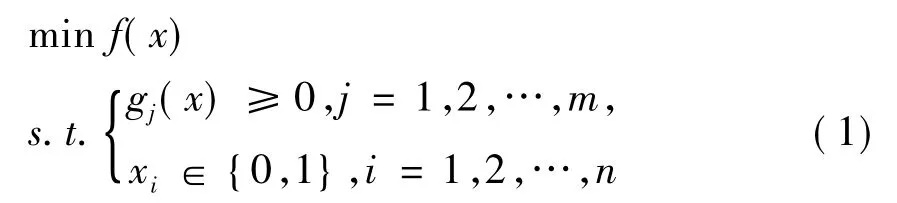
其中x=(x1，x2，…，xn)，n决策变量个数，f(x)，gj(x)(j=1，2，…，m)目标分别为目标函数和约束函数，m为不等式约束数目。取文献［7］中的参数αi=1(i=1，2，…，n)，上述问题可等价地表示为如下连续变量优化问题

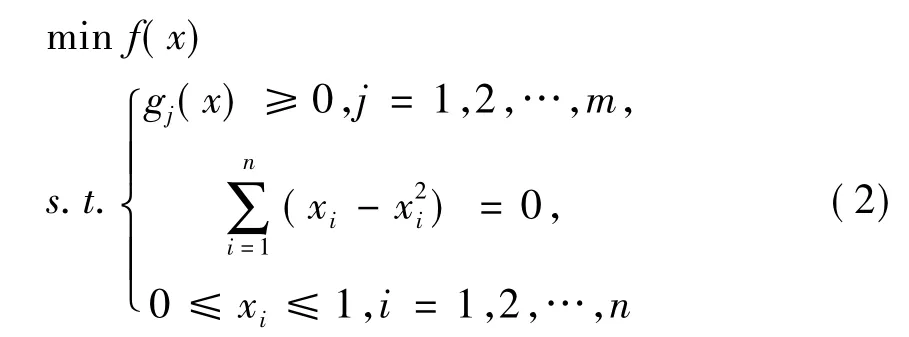
问题(1)和(2)的等价证明参见文献［7］。

由于上述连续变量问题为约束优化问题，没有统一的较好的解法，而无约束问题中有很多经典的并且收敛较好易于上机实现的算法，本文下面考虑应用罚函数的特点将约束条件吸收到目标函数中，使约束问题变为无约束问题，再应用牛顿法搜索最优解。

为了方便应用罚函数将问题(2)转化为序列无约束问题，本文将问题(2)改写成如下形式

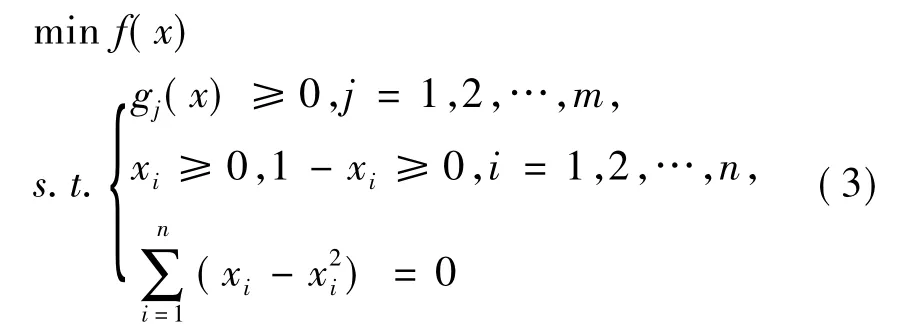
2 连续化后0-1规划的罚函数解法

2.1 罚函数法

罚函数法包括外点罚函数法、内点罚函数法和混合罚函数法。罚函数法的基本思想是根据约束特点构造某种罚函数，然后把它加到目标函数中，使得对约束最优化问题的求解转化为对一系列无约束问题，其极小点或者无限地向可行域靠近，或者一直保持在可行域内移动，直到收敛于原来约束最优化问题的极小点。外点罚函数法是通过一系列惩罚因子，求无约束增广目标函数的极小点来逼近原约束问题的最优点。随着惩罚因子的不断增大，迫使惩罚项的值不断减小，从而使增广目标函数的极小点沿着某一运动轨迹从原约束问题的可行域外逐渐逼近可行域内的最优点，当惩罚因子趋于无穷大时，无约束问题的极小点就是原约束问题的最优点。内点罚函数法通过构造一个障碍函数转化为无约束问题，由于障碍函数的作用使得当从原约束问题的可行域中某点出发，每次迭代过程均在可行域中进行，随着障碍因子的不断减小，使得无约束问题的极小点序列不断逼近原约束问题的最优解。由于外点罚函数法的初始点可以任选，适用于求解等式约束问题;而内点罚函数法要求初始点在可行域内，适用于求解不等式约束优化问题。综合考虑两者的优点，将两种算法结合起来，形成了混合罚函数法。

上述连续化方法将0-1规划问题转化为一个在［0，1］区间上的非线性约束规划问题。考虑到约束非线性问题求解的困难，本文利用罚函数将约束问题转化为较好求解的无约束问题。又问题(3)带有等式和不等式约束，本文采用混合罚函数法将两种类型的约束吸收到目标函数中再应用牛顿法求解序列的无约束问题。对于一般的约束优化问题

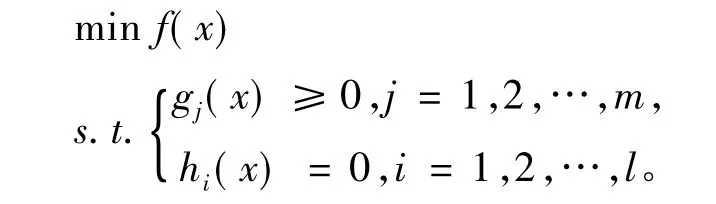
本文采用如下内点形式的混合罚函数

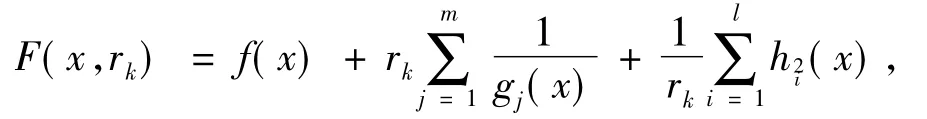
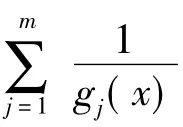
因此问题(3)转化为如下无约束问题

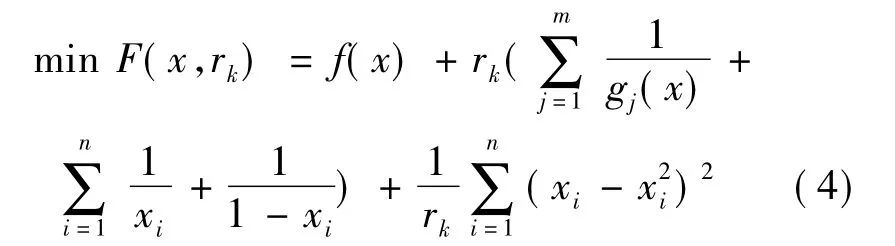
2.2 混合罚函数算法

混合罚函数算法如下:

(1)选定初始点x0，要求满足不等式约束，初始障碍因子r1，惩罚因子缩小系数c＜1，终止限ε=10－6，置k=1。

(2)假设已获迭代点xk－1，以xk－1为初始点，求解minF(x，rk)，设其最优解为x(rk)。

(3)若xk－xk－1≤ε，则x(rk)是问题(1)的最优解，打印x(rk)，f(x(rk))，否则转(4)。

(4)rk+1=crk，k=k+1，转(2)。

3 数值算例

算例1

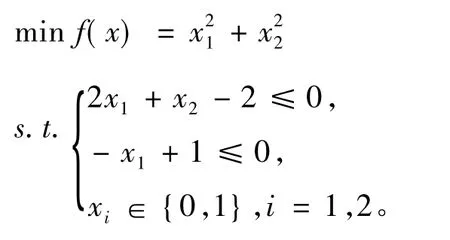
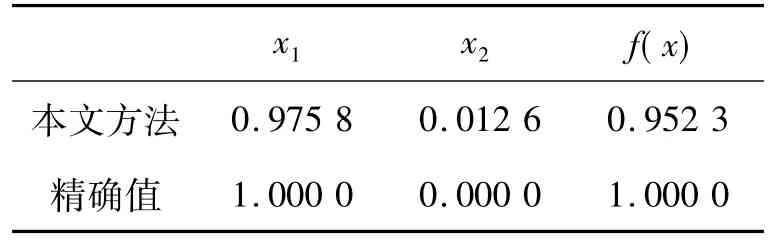
表1 算例1的计算结果及精确解

算例2

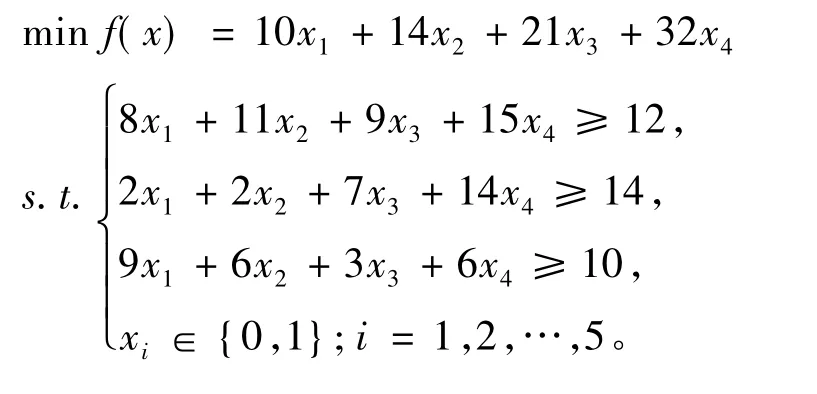
表2 算例2的计算结果及精确解

分析表1和表2可知，无论目标函数是线性还是非线性函数，应用本文提出的方法都搜索到了较好的近似解，说明该方法是可行和有效的，为求解0-1规划问题提供了一个新途径。

4 罚函数法在指派问题上的应用

实际中会遇到这样的问题，有n项不同的任务，需要n个人分别完成其中的1项，每个人完成的时间不一样，因此应指派哪个人去完成哪项任务，使完成n项任务花费总时间最小的问题称作指派问题。

现假设指派4个人完成4项工作，每人完成每项工作所需时间如表3

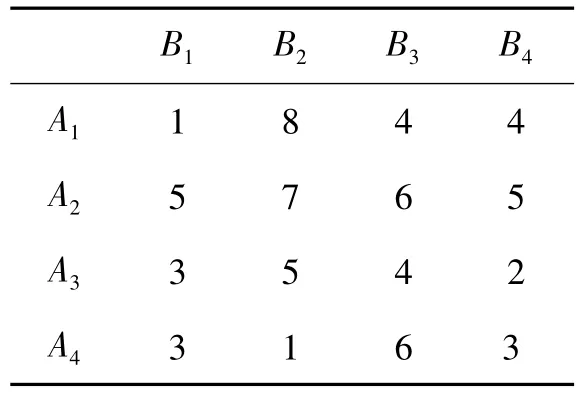
表3 工作所需时间表

其中Ai(i=1，2，…，4)表示工人，Bj(j=1，2，…，4)表示工作。

该指派问题可设变量

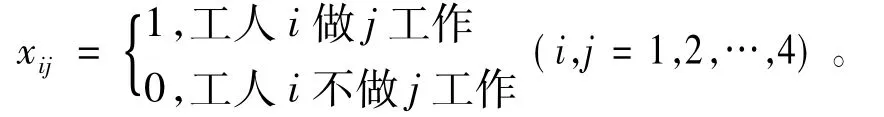
因此可建立如下0-1规划模型，计算结果见表4。

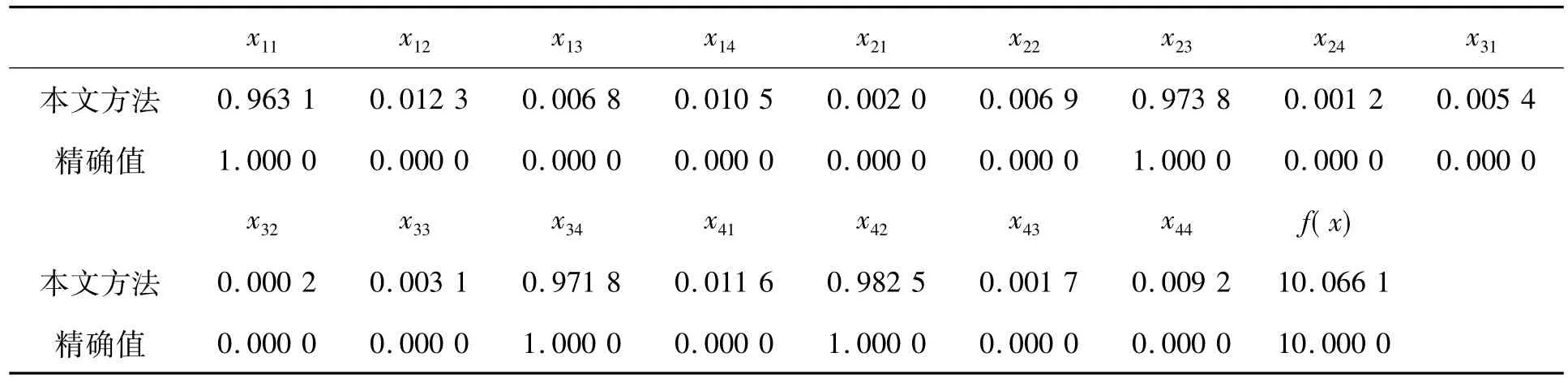
表4 指派问题计算结果及精确解

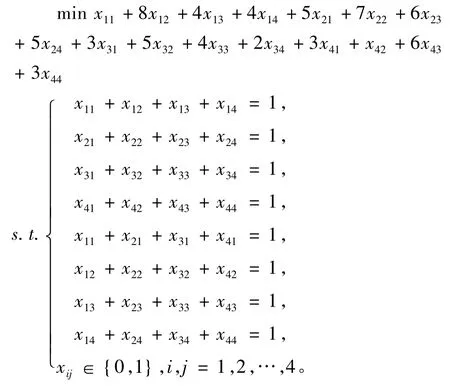
分析表4可知当A1完成B1工作，A2完成B3工作，A3完成B4工作及A4完成B2工作时花费总时间最小为10.066 1，与精确值的误差仅为0.06，说明了本文方法的有效性。

5 结论

本文应用一个非线性等式约束将0-1规划问题等价表示为［0，1］区间上的连续变量优化问题，再利用混合罚函数法将带有非线性约束的连续问题转化为求解一序列无约束问题，应用无约束方法中经典的牛顿法求解原问题的近似最优解。数值结果表明本文提出的方法对目标函数为线性或非线性的情况下都是有效可行的。由于牛顿法对初始点的选取要求比较苛刻以及当障碍因子越来越来小导致Hesse矩阵的病态，从而不能构造Newton方向使迭代无法进行，这两个问题将影响到最后解的质量。因此如何提高此类方法解的精确性是今后继续研究的一个方向。

［1］李晓萌，戴光明，石红玉.解决多维0/1背包问题的遗传算法综述［J］.电脑开发与应用，2006，19(1):4-5，8.

［2］梁国宏，张 生，黄 辉，等.一种改进的模拟退火算法求解0-1背包问题［J］.广西民族大学学报(自然科学版)，2007，13(3):91-93.

［3］田烽楠，王 于.求解0-1背包问题算法综述［J］.软件导刊，2009，8(1):59-61.

［4］高 峰，张连生.多项式0-1整规划的两个连续化途径［J］.上海大学学报(自然科学版)，1999，5(2):95-98.

［5］Kiwiel K C，Lindberg P O，Nou A.Bregman proximal relaxation of large-scale 0-1 problems［J］.Computational Optimization and Applications，2000，15(1):33-44.

［6］李艳艳，李兴斯.求解线性0-1规划的一种连续化方法［J］.大连理工大学学报，2009，49(2):299-302.

［7］隋允康，贾志超.0-1线性规划的连续化及其遗传算法解法［J］.数学的实践与认识，2010，40(6):119-127.

［8］郭 科，陈 聆，魏友华.最优化方法及其应用［M］.北京:高等教育出版社，2007:120-130.

A continuous approach to 0-1 program and its solution with penalty function algorithm

ZHU Li-hua
(Mathematics and Physics Department，Fujian University of Technology，Fuzhou350118，China)

To optimize the 0-1 programming，a method of penalty function is proposed，according to the feature of discrete variables.In this paper，a 0-1 discrete programming problem is converted to an equivalent continuous nonlinear programming formulation on the domain of［0，1］by a nonlinear equality constraint，then the constraint nonlinear problem is transformed into unconstraint nonlinear problem by means of penalty function.Two examples are presented and the numerical results show that the approach is affective and accurate.

0-1 programming;continuous;constraint nonlinear programming;penalty function

O221.4

：A

：1004-4329(2015)01-020-04

2014-09-22

福建工程学院青年基金(GY-Z13009)资助。

祝丽华(1979－)，女，讲师。主要研究方向：最优化、数学规划。