NA随机变量加权部分和的大偏差估计

李瑞军

(山西工程技术学院基础部，阳泉 045000)

NA随机变量加权部分和的大偏差估计

李瑞军

(山西工程技术学院基础部，阳泉 045000)

首先，本文研究了NA随机变量加权部分和的极大值型不等式。在此基础上我们研究了NA随机变量加权部分和的极大值型大偏差估计。当权函数满足ai≡1时，我们可立即得到NA随机变量部分和的极大值型大偏差估计。

NA随机变量;加权部分和;大偏差估计

概率论是从数量方面研究随机现象的规律的数学分支学科。它不仅与物理、生物、计算机、经济等许多学科有交叉结合，而且在自然科学、社会科学和管理科学等方面都有着广泛的应用，因此从上世纪三十年代以来，发展较为迅速，还不断涌现新的分支学科。概率极限理论就是其主要的分支之一，也是概率论与数理统计学科中较为重要的理论基础。研究独立随机变量的概率极限理论又是概率极限理论中最为经典的理论之一。独立随机变量的极限理论研究已相当成熟，而在现实生活中所发生的事情大多并非是互不相关，而是彼此之间存在某种关系的。因此，研究相依随机变量序列的性质及其应用，越来越受到学者的重视。有关相依随机变量如鞅差、φ-混合、ρ-混合、α-混合等，它们的定义及其性质，我们可参见著作Stout［1］、陆传荣和林正炎［2］、林正炎和白志东［3］、吴群英［4］，等等。

NA(negatively associated)随机变量是一类较弱的相依随机变量，它在可靠性理论、渗透理论及多元统计分析理论等均有广泛的应用。故对NA随机变量性质的研究是有意义的。NA随机变量的定义可参加文献Joag-Dev和Proschan［5］:

定义1称随机变量X1，X2，…，Xn，n≥2是NA的，如果对 {1，2，…，n}的任意两个非空不交子集A，B均有

Cov(f(Xi，i∈A)，g(Xj， j∈B))≤0，其中函数f和g关于每个变量非降且使协方差存在。进一步，称随机变量序列{Xn，n≥1}为NA序列，如果对任意的n≥2，X1，X2，…，Xn是NA的。

近年来，很多学者对NA随机变量序列进行了深入的研究，如Matula［6］给出NA随机变量序列的收敛定理如三级数定理;Su等［7］研究了NA随机变量序列的矩不等式和弱收敛性;Shao［8］给出NA随机变量的极大值型不等式;Yang［9］给出非参数回归模型未知参数加权估计的 Berry-Esseen界;吴群英［4］总结了NA随机变量序列的大数定律、收敛性、中心极限定理等等;周兴才和胡舒合［10］研究了NA样本下部分线性模型估计的强相合性;Wang等［11］给出了NA随机变量序列加权和的强极限定理;在NA样本下，Ling［12］给出样本下样本分位数的Bahadur表示，Yang等［13］给出了样本分位数的Berry-Esseen界，等等。

另一方面，有关随机变量的大偏差估计研究由来已久。例如在Lp空间上，Lesigne和Volny［14］给出了p≥2时鞅差部分和的大偏差估计，Li［15］将Lesigne和Volny［14］的结论推广到1＜p≤2的情型。Hu和Wang［16］讨论了φ-混合随机变量、NA随机变量和线性过程的大偏差估计，杨文志等［17］研究了Lp(p＞1)混合鞅的大偏差估计，李旭等［18］给出了NOD随机变量的大偏差估计，等等。

本文继续研究NA随机变量的性质，给出其加权部分和的极大值不等式。作为应用，给出NA随机变量加权部分和的大偏差估计。下面我们引出NA随机变量的极大值不等式及其推论。

引理1［8］令p＞1。设X1，X2，…，Xn是均值为零的NA随机变量，且满足，1≤i≤n，n≥1。则有

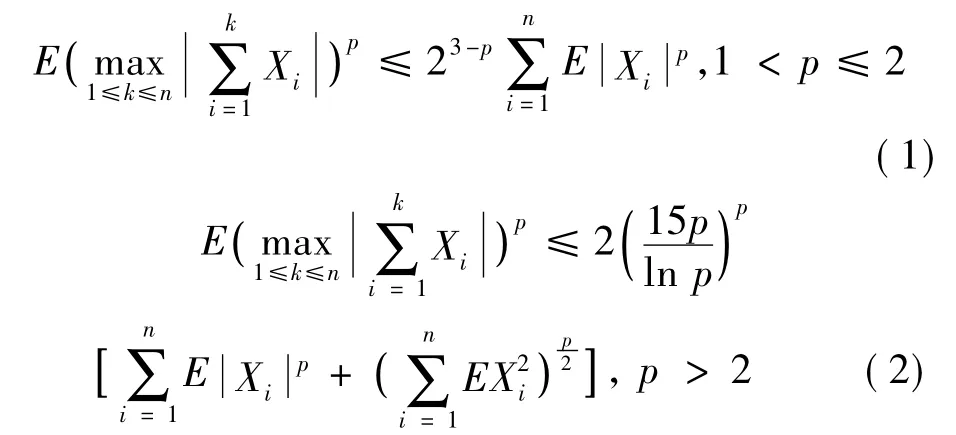
推论1令p＞1。设X1，X2，…，Xn是均值为零的NA随机变量，且满足，1≤i≤n，n≥1。对n≥1，令{ai，1≤i≤n}为一实数序列。则有

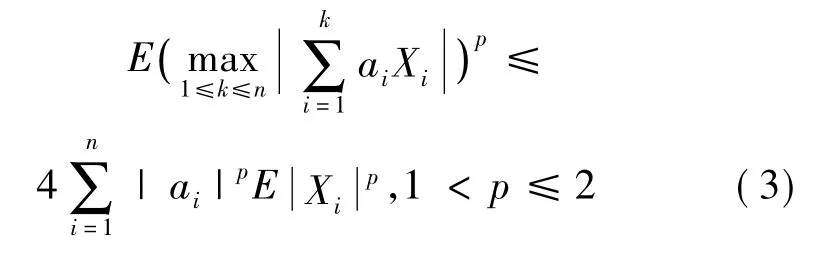
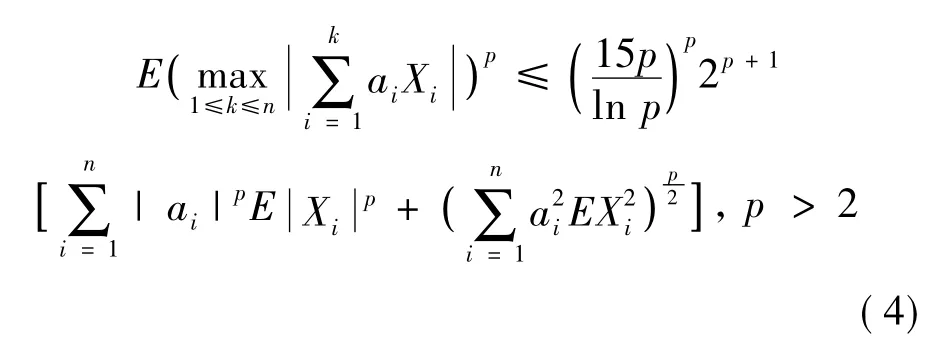
证明因为对1≤i≤n，有，其中记x+=max(x，0)，x－=max(－x，0)。易知和仍为均值为零的NA随机变量。显然对p＞1，由CP不等式知:

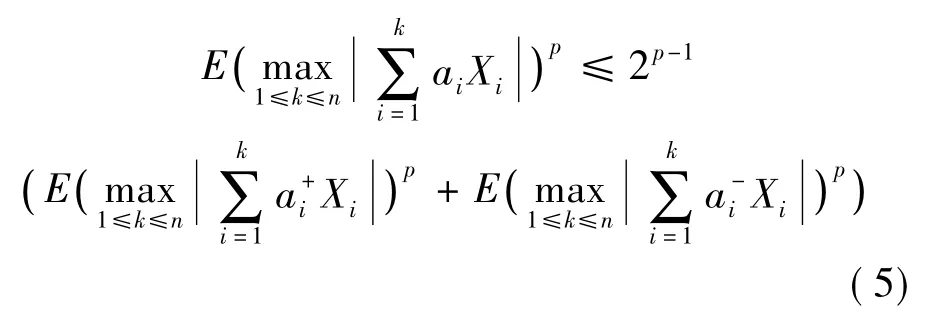
一方面，当1＜p≤2，由引理1的(1)知

类似地当1＜p≤2，有

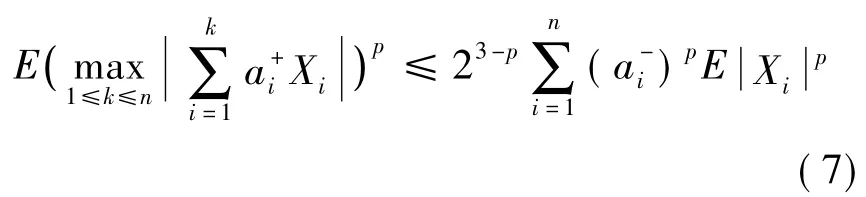
所以，由(5)式、(6)式和(7)式，可得(3)式。另一方面，当p＞2，由引理1的(2)式知

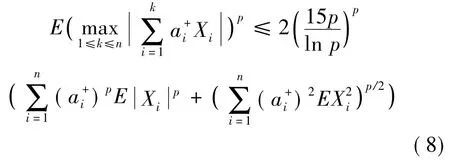
类似地当p＞2，

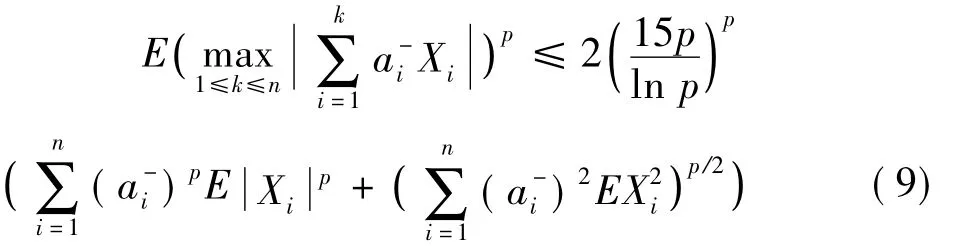
由于p≥2，函数f(x)=xp/2对x≥0为增函数，故结合(5)式、(8)式和(9)式，当p＞2，我们有

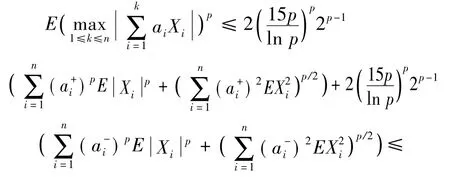
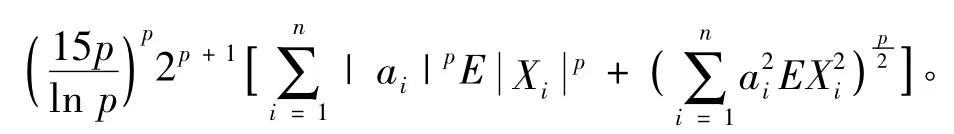
所以(4)式证毕。

2 NA随机变量加权部分和的极大值型大偏差估计

定理1令p≥1。设X1，X2，…，Xn是均值为零的NA随机变量，且存在一正常数M满足对所有的n≥1有。对n≥1，令{ai，1≤i≤n}为一实数序列。则对所有n≥1和x＞0，有

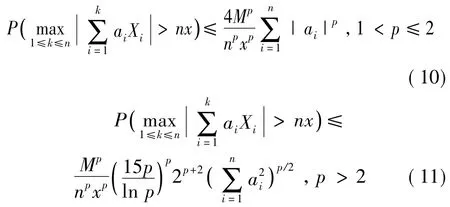
证明由Markov不等式知，对所有n≥1和x＞0有

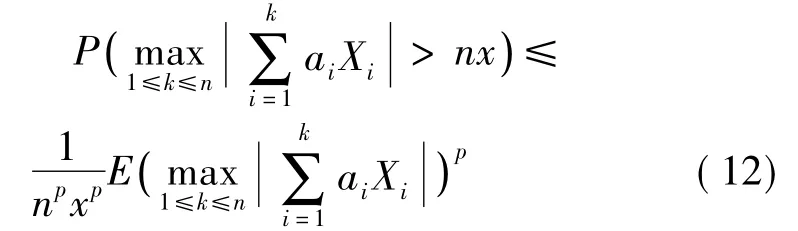
一方面，当1＜p≤2时，由，n=1，2，…，(12)式及(3)式，有

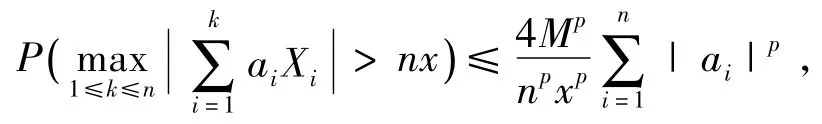
即(10)式成立。

另一方面，当p＞2，由(12)式和(4)式知

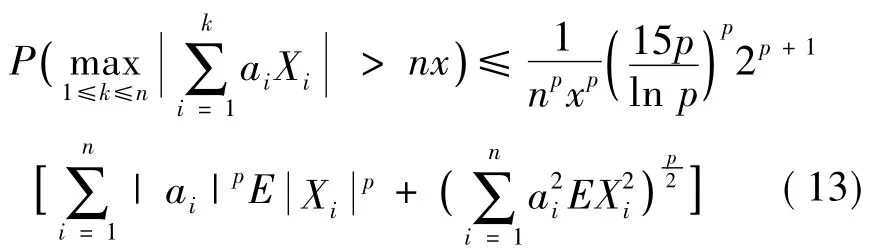
当p＞2知0＜2/p＜1。所以利用Cr不等式有

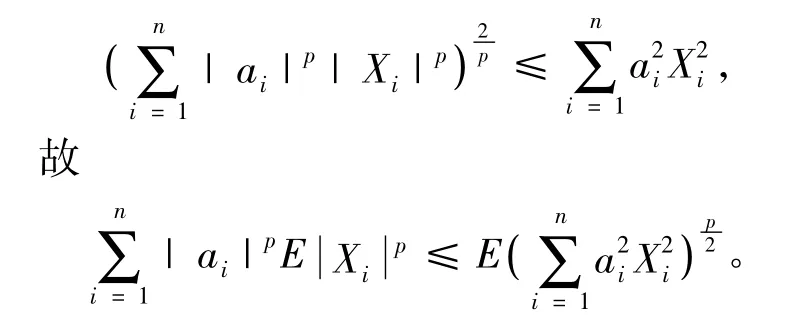
由Jensen不等式，当p＞2和x≥0时，f(x)=为凸函数，从而有

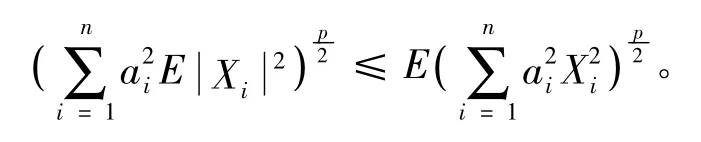
由Minkowski不等式知

所以(11)式证毕。

在定理1中，令ai≡1，1≤i≤n，n≥1，我们有如下推论:

推论2令p≥1。设X1，X2，…，Xn是均值为零的NA随机变量，且存在一正常数M满足对所有的n≥1有。则对所有n≥1和x＞0，有

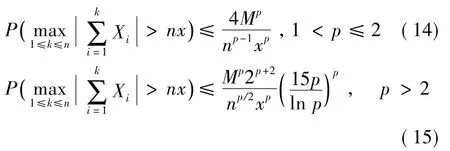
注释 我们指出，推论2不是新的。在推论2条件下，对所有n≥1和x＞0，Hu和Wang［16］的定理2.3获得了如下NA随机变量部分和的极大值型大偏差估计

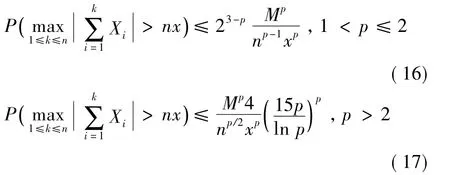
我们推论2中(14)式和(15)式的系数分别和(16)式和(17)式的系数相比，系数稍微放大了一些。主要原因是本文立足于研究NA随机变量加权部分和的极大值型大偏差估计，在估计过程中，我们将NA随机变量加权部分和分解成正部和和负部和，最终导致大偏差估计系数有所放大，但结论的主要界和Hu和 Wang［16］是一致的。另一方面，杨文志等［17］根据Lp(p＞1)混合鞅的矩不等式，在其定理1中给出了Lp(p＞1)混合鞅部分和不含极大值型的大偏差估计。李旭等［18］在其定理2.1中给出了NOD随机变量非加权部分和的大偏差估计。虽然NOD随机变量比NA随机变量要弱，但其极大值型大偏差估计含有系数含有logpn项。所以一定程度上，本文推广了Hu和Wang［16］、杨文志等［17］及李旭等［18］有关相依随机变量非加权部分和的大偏差估计到NA随机变量加权部分和的极大值型大偏差估计。

［1］Stout W F.Almost Sure Convergence［M］.New York，Academic Press，1974:30-90.

［2］陆传荣，林正炎.混合相依随机变量的极限理论［M］.北京:科学出版社，1987:2-360.

［3］林正炎，白志东.概率不等式［M］.北京:科学出版社，2006:120-145.

［4］吴群英.混合序列的概率极限理论［M］.北京:科学出版社，2006:132-255.

［5］Joag-Dev K，Proschan F.Negative association of random variables with applications［J］.Annals of Statistics，1983，11(1):286-295.

［6］Matul'a P.A note on the almost sure convergence of sums of negatively dependent random variables［J］.Statistics＆Probability Letters，1992，15(3):209-213.

［7］Su C，Zhao L C，Wang Y B.Moment inequalities and weak convergence for negatively associated sequences［J］.Science in China.Series a，Mathematics，Physics，Astronomy，1997，40(2):172-182.

［8］Shao M Q.A comparison theorem on moment inequalities between negatively associated and Independent random variables［J］.Journal of Theoretical Probability，2000，13(2):343-356.

［9］Yang C S.Uniformly asymptotic normality of the regression weighted estimator for negatively associated samples［J］.Statistics and Probability Letters，2003，62(2): 101-110.

［10］周兴才，胡舒合.NA样本部分线性模型估计的强相合性［J］.系统科学与数学，2010，30(1):60-71.

［11］Wang J X，Li X Q，Hu S H，et al.strong limit theorems for weighted sums of negatively associated random variables［J］.Stochastic Analysis and Applications，2011，29(1):1-14.

［12］Ling N X.The bahadur representation for sample quantiles under negatively associated sequence［J］.Statistics＆Probability Letters，2008，78(16):2660-2663.

［13］Yang W Z，Hu S H，Wang X J，et al.Berry-Esseen bound of sample quantiles for negatively associated sequence［J］.Journal of Inequalities and Applications，2011:83.

［14］Lesigne E，Volny D.Large deviations for martingales［J］，Stochastic Processes and Their Applications，2001，96:143-159.

［15］Li Y L.A martingale inequality and large deviations［J］.Statistics and Probability Letters，2003，62: 317-321.

［16］Hu S H，Wang X J.Large deviations for Some dependent sequences［J］.Acta Mathematica Scientia，2008，28(2):295-300.

［17］杨文志，魏永利，胡舒合，等.混合鞅一矩不等式及其应用［J］.合肥工业大学学报(自然科学版)，2010，33(5):783-785.

［18］李 旭，王学军，刘小涛，等.ND序列部分和的大偏差和强收敛性［J］.纯粹数学与应用数学，2011，27 (6):808-813.

On the large deviations estimate of partial weigted sums of NA random variables

LI Rui-jun
(Department of Basis，Shanxi Institute of Technology，Yangquan Shanxi045000，China)

First，the maximal type inequalities of partial weighted sums of NA random variables was investigated in this paper.Based on these inequalities，the large deviations of the maximal type partial weighted sums of NA random variables was studied.When the weight functions satisfyai≡1，the maximal type large deviations of the partial sums of NA random variables are obtained immediately.

NA random variables;partial weigted sums;large deviation estimate

O211.4

：A

：1004-4329(2015)01-001-04

2014-12-11

山西省自然科学基金(20120110015-5)资助。

李瑞军(1970－)，男，讲师。研究方向：概率论与混沌控制。