平衡分布与最概然分布
2015-01-05刘国杰黑恩成
刘国杰 黑恩成
(华东理工大学化学系 上海 200237)
平衡分布与最概然分布
刘国杰 黑恩成
(华东理工大学化学系 上海 200237)
以二项分布为例,阐述了平衡分布与最概然分布间的关系。通过子数很多时,二项分布可以变为正态分布以及它的相对涨落与子数的平方根成反比的统计力学原理,阐明了热力学系统的平衡分布可用其最概然分布来代表。
平衡分布 最概然分布 热力学系统的相对涨落
在统计力学中,有一条基本定律,叫做玻尔兹曼能量分布定律。这条定律指出:热力学系统的平衡分布应是玻尔兹曼分布[1]。这条定律是平衡态统计力学的基础。

即为系统拥有的总微观状态数。而玻尔兹曼分布只不过是其中拥有微观状态数最多的一种分布。由于统计力学假定所有这些微观状态出现的概率相等,故玻尔兹曼分布也是平衡系统中出现概率最多的分布,称为最概然分布。本文试图从理论上表明,为什么最概然分布能够代表热力学系统的平衡分布。
1 平衡分布和最概然分布示例
为了便于说明,以最简单的二项分布作为示例。设有N个定域子,分布在同一能级的两个简并量子态A和B上,如图1所示。

MN-MAB
图1 定域子在同一能阶的两个简并量子态上的分布示意图
不同的M值代表了不同的分布,因此,M是一个指明系统分布的特征参数。又因A和B是同一能级的两个简并量子态,因此,所有微观状态有相同的能量,他们都服从等概率原理。
对于这样的定域子系统,其总微观状态数应为:
(1)
式中N!为N个定域子的总排列数。由于N个定域子中有M个分配在A态,(N-M)个分配在B态,而A态上M个子的排列以及B态上(N-M)个子的排列都不算新的微观状态,所以N!必须除以M!和(N-M)!。
式(1)是可以利用牛顿二项式求解的,它实际上相当于牛顿二项式
中的系数之和。于是,只要令x=y=1,即可得到:
(2)

(3)
这个分布就是上述系统的最概然分布,它在系统中出现的概率为:
(4)
式(4)表明,在这个平衡系统中,最概然分布出现的概率与子数N的平方根成反比。这就是说,随着N增大,最概然分布出现的概率反而减小。当N≈1024时,Pmax≈10-12,这是一个很小的概率。那么,为什么还说最概然分布可以代表热力学系统的平衡分布呢?图2 是不同N时的平衡分布及最概然分布图[2]。为清楚地显示大数,图2中的纵坐标和横坐标都用相对值表示,前者为ω(M)/ωmax,后者为M/N,其中M/N= 0.5的虚线所示即为最概然分布。
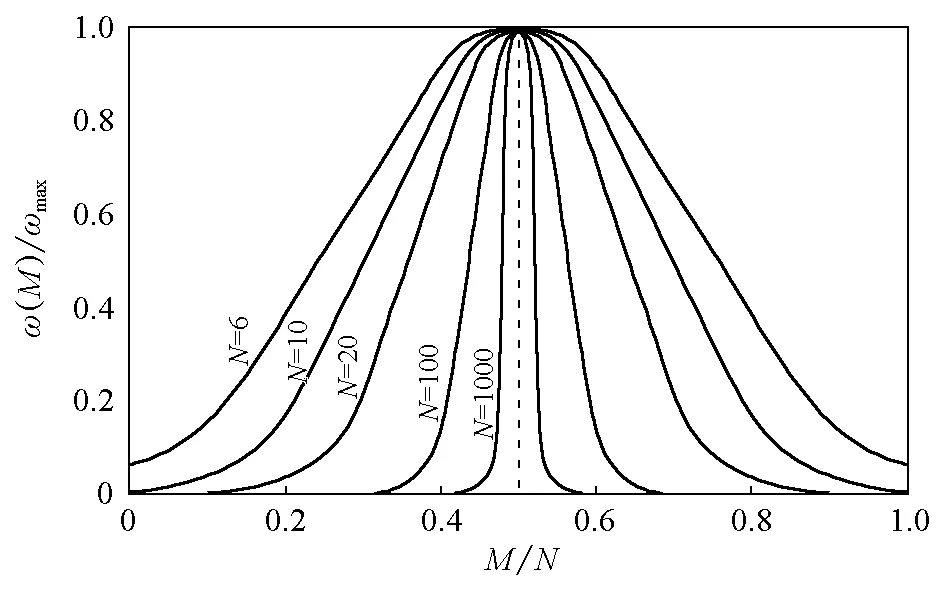
图2 不同N时各种分布的相对微观状态数
由图2可见,随着N增大,分布曲线变得越来越窄,换句话说,平衡分布越来越接近最概然分布。
2 二项分布与正态分布[3]
所谓二项分布是这样一种分布,它必须满足如下两个条件:
① 每一次试验只有两种可能,非此即彼;
② 在n(n为正整数)次独立的试验中,每一次出现两种可能的概率分别为p和q。于是,在n次试验中,出现某种可能为h次的概率当为:
(5)
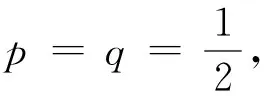
(6)
若假定n,h和k都是大数,将式(5)取对数,则:
lnP(h) = lnn! - lnh! - lnk! +hlnp+klnq≈nlnn-hlnh-klnk+hlnp+klnq
(7)
式(7)中应用了Stirling近似公式lnh! =hlnh-h和lnk! =klnk-k。如果注意到n是一个常数,dk= - dh,则:
dlnP(h) = - lnhdh- lnkdk+ lnpdh+ lnqdk= (- lnh+ lnk+ lnp- lnq)dh
(8)
(9)
当P(h)为极大值时,式(9)等于0,即:
(10)
式中h0和k0是极大值处h和k的值。由于p+q= 1,h0+k0=n,可得:
h0= np, k0= nq
(11)
若将注意力集中在极大值的附近,令:
h = h0+ x, k = k0- x
(12)
则因dh= dx, dk= - dx,式(9)可写成:
(13)
将式(13)积分,则得:
(14)

P(h) =Ae-ax2
(15)
式中常数A可由归一化条件确定:
故:
(16)
将式(16)代入式(15),得:
(17)
这是一个常见的正态分布函数,式中h0为平均值,σ为根方差,是决定正态分布曲线形状的两个参数。图3示意地画出了参数h0和σ的值与正态分布曲线形状间的关系。由图3可以看出,正态分布曲线都是左右对称的,对称轴为h=h0的垂线。h0愈大,曲线的最高点位置愈向右;σ愈小,则曲线的最高点愈高,且曲线形状愈窄。
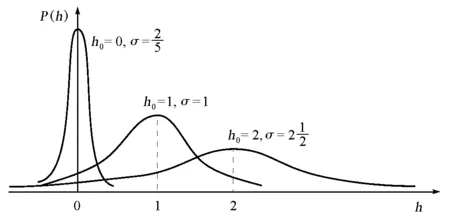
图3 h0 和σ的值与正态分布曲线形状的关系
上述推导表明,二项分布和正态分布虽是两种不同的分布,但在n、h和k都为大数的情况下,可将二项分布视为正态分布。这个结论对于本文所要论证的问题是至关重要的。
3 最概然分布及其涨落
现在回到第1节所述,当图1 中的N、M和N-M都是大数时,二项分布可视为正态分布,式(6)可表示成式(17)形式,故有:
(18)
式中m=M-M0,M0=N/2为平均值。当m= 0或M=N/2时为最概然分布,此时,由式(18)和式(4)可得:
(19)
所以,a= 2/N,故式(18)也可表示为:
(20)
式(20)可进一步表示为:
(21)
由于N是个约为1024的大数,式(21)在一般情况下近似等于0。仅当M十分趋近N/2时,P(M)/Pmax(即ω(M)/ωmax)才趋近于1。倘若将P(M)/Pmax( 即ω(M)/ωmax)对M/N作图,则结果如图4所示。

图4 N为大数时,P(M)/Pmax对M/N作图


(22)
然而,

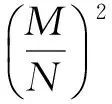
(23)
(24)
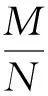
(25)
统计力学能够证明[4],平衡系统各种性质的相对涨落决定于系统所含的粒子数,它的大小与子数N的平方根倒数同数量级。对于本文涉及的平衡分布,当N=1024时,有:
(26)
这是一个非常小的值,以致可以忽略不计。式(25)中的平均号〈 〉去掉亦无妨,即Δ= 0,故:

(27)
换句话说,将图4所示的正态分布视为M/N为0.5的垂线亦无妨。正是由于这个道理,热力学系统的平衡分布可用其最概然分布来代表。
[1] 唐有祺.统计力学及其在物理化学中的应用.北京:科学出版社,1979
[2] Fast J D.Entropy.2nd ed.Netherlands:Philips Technical Library,1962
[3] 铎木启三.化学中的数学.梁慧姝,郝雷译.上海:上海教育出版社,1986
[4] 胡英,刘国杰,徐英年,等.应用统计力学-流体物性的研究基础.北京:化学工业出版社,1990
Equilibrium Distribution and the Most Probable Distribution*
Liu Guojie Hei Encheng**
(SchoolofChemistry,EastChinaUniversityofScienceandTechnology,Shanghai, 200237,China)
Taking binomial distribution as an illustration, we elaborated the relationship between equilibrium distribution and the most probable distribution. According to the statistical mechanics, the binomial distribution approximates to the normal distribution when the number is large enough, and the relative fluctuation is inversely proportional to the square root of the number, we illustrated that the equilibrium distribution of a thermodynamic system could be described by the most probable distribution.
Equilibrium distribution; Most probable distribution; Relative fluctuation of thermodynamic system
10.3866/pku.DXHX20150683
*通讯联系人,E-mail:heiec@ecust.edu.cn
教育部教育质量工程建设项目(No.YJ0136104);国家精品资源共享课建设项目(No.YJ0125206)
O6; G64
