一种基于RBF神经网络的打印机光谱预测模型
2015-01-05于海琦田全慧
于海琦,刘 真*,田全慧
(1.上海理工大学 出版印刷与艺术设计学院,上海200093;2.上海出版印刷高等专科学校,上海200093)
传统的色彩复制是基于色度的复制,只能满足特定观察条件下色彩匹配,即存在同色异谱,而基于光谱的色彩复制能够有效避免同色异谱问题[1]。
现有的光谱预测模型分为两大类:一类是物理模型,目前对物理模型的研究主要集中在光谱Neugebauer模型以及在此基础上进行的修正模型[2,3]。另一类是数学模型,如多项式回归模型、神经网络模型、查找表模型等。
由于打印设备的非线性较高且印刷复制条件复杂、稳定性较差,采用物理模型需对模型进行较多修正,需要大量的训练样本,导致模型复杂。而神经网络模型不需要考虑呈色的复杂内部机制,只需要通过优化网络参数、样本选择等,得到满足应用要求的网络。目前印刷中应用较多的主要是BP和RBF两大类神经网络模型。文献[3]提出使用BP神经网络和RBF神经网络解决颜色复制中的非线性映射问题,文献[4]借助BP神经网络对打印机进行特性化。BP神经网络容易陷入局部极值,相同网络结构和参数的BP 网络会得到不同的预测结果,导致预测结果不稳定,故BP神经网络并不适用于需要定量表示颜色的预测模型,而RBF神经网络建模速度快、预测结果稳定。故本文最终采用RBF神经网络进行打印机颜色预测建模。现有的神经网络预测模型多是通过优化神经网络的参数进而提高模型精度,而本文从输入变量的角度进行研究,将通道驱动值的扩展项作为神经网络的输入变量,进行网络训练优化RBF神经网络模型,并确定最优化的扩展项用于打印机的颜色预测,实验结果表明本文方法具有较高的预测精度。
1 RBF神经网络及输入变量扩展
RBF神经网络的基本思想是以径向基函数作为隐单元的“基”,构成隐含层空间,隐含层将低维输入向量变换到高维空间,解决低维线性不可分的问题。RBF神经网络是一种局部逼近网络,只需对少量的权值和阀值进行修正,不存在BP神经网络的局部极值问题。RBF神经网络的基本特征是:神经元的输出值的大小与输入值到中心点的距离有关,距离中心点越近,神经元的输出值越大;神经元的激活区域呈现径向对称。
隐含层神经元径向基函数通常采用高斯函数,基于上述特征,神经元响应模型可表示为:

其中,x为输入样本;ci为中心点;φi(x)为网格输出;σ为宽度,决定了径向基函数围绕中心点的宽度[1]。
在RBF神经网络训练前,需要首先确定分布密度Spread的值,Spread值越大,网络的逼近误差会比较大,容易造成大量的运算。Spread值越小,网络逼近误差比较小,但网络的收敛速度较慢,泛化能力较差。目前,主流的确定最佳Spread值的方法是试凑法[5],本文以通道驱动值作为神经网络的输入变量,光谱反射率作为输出变量,进行神经网络模型的训练,以色差最小为目标,循环迭代确定最佳Spread值。
通道驱动值具有可扩展性[6],本文将通道驱动值进行扩展作为RBF神经网络的输入变量,扩展的方式有很多种,其中使用最多的是在向量中增加通道的高阶项以及通道之间的交叉项,如(cm,c2,cm2,cmy)等。文献的研究表明在多项式回归模型中增加扩展项,能够有效地提高模型转换精度,但是目前尚无在RBF神经网络中应用通道驱动值扩展的方法,本文通过驱动值扩展增加输入变量项数,并分析不同扩展项作为输入变量对模型精度的影响。经扩展后的输入变量如式(2)所示。

2 实验
2.1 样本获取
采用 HP Designjet Z3200Photo打印机打印。c、m、y按照网点面积率 [0%、20%、40%、60%、80%、100%]排列组合成216个色块作为训练样本。c、m、y网点面积率[0%、25%、50%、75%、100%]排列组合成125个色块作为检测样本。
2.2 样本测量
选用X-rite公司的分光光度计i1以及辅助装置机械臂iO作为测量设备,测量色块的光谱反射率,取400~700nm范围内的光谱,间隔为10 nm,共31维。
2.3 神经网络建模
采用matlab神经网络工具箱进行预测模型的建模。以式2中驱动值的扩展项分别作为RBF神经网络的输入变量,光谱反射率作为输出变量进行神经网络的训练和检测,输入变量矩阵表示为I,I表示一个M*S大小的矩阵,S为样本数,M为输入变量的扩展项数,分别为3、5、6、8、6、8、9、11、14、17、18、20,输出变量矩阵表示为 O,矩阵 O是一个N*S大小的矩阵,N表示光谱反射率的维数为31。
2.4 模型评价指标
以CIE2000色差 ΔE00(D50,2°)和光谱均方根误差RMSE评价预测的色度精度和光谱精度[7,8]。
3 结果与讨论
分布密度Spread是影响RBF神经网络性能的关键参数,本文采用试凑法进行Spread参数的确定,在每一种驱动值扩展项作为输入变量时,确定最优化的Spread值进行网络训练,实验结果如表1和图1所示。

表1 不同扩展项预测光谱的色度和光谱精度Colorimetric and spectral accuracy of spectral prediction with different extensions
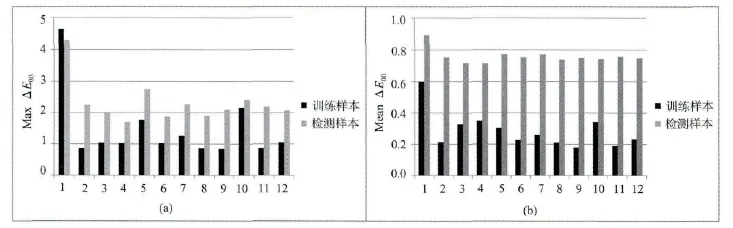
图1 不同扩展项的最大色差和平均色差
由表1和图1可知,与原输入变量作为输入变量的预测精度相比,扩展项的增加提高了模型的色度精度和光谱精度,不同扩展项的引入对预测精度的影响亦较大,增加不同的扩展项时,达到最优色度精度的分布密度亦不同,整体随扩展项增加而增加。比较p2、p1和p0可知,[1cmy]项的引入明显降低ΔE00和RMSE,提高光谱预测的精度;分别比较p3和p5、p2和p4,从训练样本看,[c2m2y2]比[cm cy my]对光谱预测精度的提高更明显,从检测样本看两种二次项的引入导致检测样本的预测精度下降,即网络的泛化能力降低,而p5比p4项精度高,说明[cmy]引入提高了网络的泛化能力;比较p7、p8和p9可知,[c3m3y3]的引入提高预测精度,而引入[cm2cy2mc2my2yc2ym2]导致精度明显下降,出现极值点,网络泛化能力下降;比较项数为17、18、20与项数小于11的扩展项,说明并不是扩展项越多,预测精度越高,反而由于扩展项的增多会导致误差出现极值或导致网络泛化能力下降。
从以上分析可以得出,三次项中,[cmy]项的引入对预测精度的提高最显著,且能够提高网络的泛化能力,[cm2]类型交叉项的引入反而易出现极值,同时导致网络泛化能力下降;二次项中,平方项和交叉项都能够提高预测精度;由此,引入[1 cmy]、[c2m2y2]和[cm cy my]项,即p7项作为输入变量建立的RBF神经网络模型是最优化的,在保证预测精度的同时提高网络的泛化能力。

图2 原输入变量与扩展输入变量预测光谱反射率曲线比较

表2 预测色度误差大于2的样本输入变量Input variable of samples predicted colorimetric accuracy>2
分析原输入变量预测精度较差的色块主要集中在三个通道驱动值都较大的色块,即暗调部分(如表2所示),引入[1cmy]和[cm cy my]扩展项后预测的光谱曲线与原通道驱动预测的光谱曲线如图2所示,说明扩展项的引入提高了模型的预测精度。印刷中使用的是半色调加网技术来表现颜色的阶调层次,采用c、m、y三色油墨以一定的网点百分比印刷时,会存在c、m、y、单色油墨以及cmy、cm、cy、my三色或者两色油墨网点叠印共存的情况,Demichel模型亦是基于这种情况的概率模型,故[cmy]和[cm cy my]项的引入能够有效提高模型的预测精度。
4 结论
本文采用RBF神经网络进行打印机光谱预测模型的研究,通过扩展原c、m、y输入变量的项数提高模型的预测精度,实验结果表明[1cmy]项的引入能够有效提高模型的预测精度,同时提高网络的泛化能力。引入[cmy]、[c2m2y2]和[cm cy my]项的模型在预测精度和模型泛化能力上均是最优化的。而引入[cm2cy2mc2my2yc2ym2]项会导致模型预测精度以及泛化能力降低。由此选择[1cmy c2m2y2cm cy my c m y]作为模型的输入变量的RBF神经网络训练是满足高精度预测的最优模型。
[1] 李金城.色彩高保真复制的理论与实践[D].南京:南京林业大学,2013.Li J C.Theory and practice of high-fidelity color reproduction[D].Nanjng:Nanjing Forestry University,2013.
[2] Liu Q,Wan X X,Xie D H.Optimization of spectral printer modeling based on a modified cellular Yule Nielsen spectral neugebauer model[J].Journal of the Optical Society of America.A,2014,31(6):1284-1294.
[3] Roger D H.Improving the Yule-Nielsen modified spectral neugebauer model by dotsurface coverages depending on the ink superposition conditions[J].Color Imaging X:Processing,Hardcopy,and Applications,2005:434-447.
[4] 何颂华,张 刚,陈 桥,赵子琦.基于BP神经网络的多基色打印机光谱特性化[J].包装工程,2014,35(13):110-115.He S H,Zhang G,Chen Q,Zhao Z Q.Spectral characterization of multicolor printer based on BP neural network[J].Packaging Engineering,2014,35(13):110-115.
[5] 卓金武.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2011.ZhuoJ W.Application of MATLAB in Mathematical Modeling[M].Beijing:University of Aeronautics and Astronautics Press,2011.
[6] 陈奕艺.基于数码相机的物体表面色光谱重构[D].杭州:浙江大学,2008.Chen Y Y.Spectrum reconstruction of surface color based on the digital camera[D].Hangzhou:Zhejiang University,2008.
[7] 万晓霞,易尧华.全彩色遥感影像彩色合成效应的研究[J].武汉大学学报(信息科学版),2002,27(2):203-207.Wang X X,Yi Y H.Color compound domino effect of true color remote sensing imagery[J].Geomatics and Information Science of Wuhan University,2002,27(2):203-207.
[8] 刘浩学.CIE均匀颜色空间与色差公式的应用[J].北京印刷学院学报,2003,11(3):3-9.Liu H X.The application of CIE uniform color space and its color difference formula [J].Journal of Beijing Institute of Graphic Communication,2003,11(3):3-9.
