基于自适应粒子群优化的图像匹配算法

冯 浩

宿州学院机械与电子工程学院，安徽宿州，234000

基于自适应粒子群优化的图像匹配算法

冯 浩

宿州学院机械与电子工程学院，安徽宿州，234000

结合图像匹配技术特点，引入粒子群优化(PSO)算法，在此基础上提出了一种基于自适应粒子群优化(APSO)的图像匹配算法。该算法通过建立非线性递减惯性权值动态模型，并结合变异思想增加种群多样性，实现对个体粒子进行自适应过滤，避免产生早熟收敛现象，降低局部极小的可能性，从而更好地优化由局部到全局的开放式搜索性能。将APSO算法运用于图像匹配过程中，可实现图像的快速准确匹配。实验结果表明，APSO算法能够减少图像匹配处理时间，并在匹配精度和抗干扰性能指标上优于对比算法。

图像匹配；粒子群优化算法；惯性权值；变异；自适应

作为数字图像处理和计算机视觉研究领域的重要技术之一的图像匹配，在医学图像分析、卫星遥感、目标跟踪、视觉数据挖掘、资源分析等领域均有广泛的应用[1]。图像匹配是指将模板图像与基准图像进行匹配分析，并计算二者的相似度，从而达到图像识别或定位的目的[2]。

目前常用的图像匹配方法大致分为两类：一类是基于特征的图像匹配算法[3]，另一类是基于灰度(像素灰度值)的图像匹配算法[4]。第一类算法主要是通过提取模板图像和基准图像中的共有特征(包括点、线和面等匹配单元)，建立两幅图像的对应关系，算法匹配速度较快，但是匹配精度不高，常用算法有Hausdorff距离匹配法、金字塔小波算法等。第二类算法无需进行图像的特征点提取，该算法主要利用图像的像素灰度值信息进行匹配，通过一定的相似性度量准则实现最优匹配，其优点是匹配精度高，缺点是匹配速度较慢，常用算法有平均绝对差(MAD)算法、归一化互相关(NCC)算法以及序贯相似检测(SSDA)算法等。另外，国内外学者也提出多种图像匹配智能优化算法，包括模拟退火算法(SA)、遗传算法(GA)[5]、自适应遗传算法(AGA)[6]等。其中，遗传优化算法具有非遍历随机搜索机制，可以代替传统的图像匹配算法(SIFT算法等)，但是其适应度受限较大，存在局部搜索能力不足的缺陷，容易陷入局部极小，产生早熟收敛现象。

本文在分析以上算法特点的基础上，提出了一种基于自适应粒子群优化(Adaptive Particle Swarm Optimization，APSO)的图像匹配算法。实验结果证明，该算法能够使各粒子以较大概率跳出局部最优，进行全局最优位置搜索，在保证匹配精准率的前提下，实现图像的最优位置匹配。

1 自适应粒子群优化(APSO)算法

1.1 基本粒子群优化算法

假设在D维空间中的某个群体由n个粒子组成，其中，用Xi=(xi1,xi2,…,xid)T表示第i个粒子在D维空间中的当前位置；用Vi表示第i个粒子在D维空间中的飞行速度，记作Vi=(vi1,vi2,…,vid)T；用Pi=(Pi1,Pi2,…,Pid)T表示第i个粒子在D维空间中搜索到的最优位置；整个粒子群在D维空间中搜索到的最优位置用Pg=(Pg1,Pg2,…,Pgd)T表示。则基本粒子群优化(Particle Swarm Optimization，PSO)算法可以由以下更新迭代公式表示[7]：

(1)

(2)

其中，i=1,2,…,n；d=1,2,…,D。

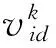
1.2 自适应粒子群优化(APSO)算法

在基本PSO算法中，惯性权值、学习因子均为常数，而参数设置不同对算法影响较大，对于惯性权值ω的设置，较大的ω有助于加快算法收敛速度，而较小的ω有助于提高算法的收敛精度。本文结合标准PSO算法搜索进程的非线性特点，改变惯性权值常用的递减策略，随着迭代次数的增加，建立惯性权值的自适应调节模型，如式(3)所示：

ω=ωmax-(ωmax-ωmin)

(3)

其中，ωmax、ωmin分别为最大、最小惯性权值，一般取ωmax=0.9，ωmin=0.4；σ1、σ2为校准系数，用于调节惯性权值的变化率；k表示粒子当前迭代次数；kmax为最大迭代次数；该数学模型可限定惯性权值ω在(0.4,0.9)区间上进行动态调节。

为了进一步降低局部极小的可能性，本文引入变异机制对粒子的最优解进行选择过滤。

通过对算法初期的初始化粒子最优值数据进行衡量，计算粒子最优适应度值的平均值，并将其与每个粒子的最优适应度值进行比较，若当前粒子最优位置值次于平均值，则对粒子的当前位置进行变异重生操作，反之则更新该粒子的当前位置和速度。当需要执行变异时，对粒子当前位置采用式(4)进行重生。

(4)

其中，γ为(0,1)之间服从高斯分布的随机数。

利用这种自适应的变异机制，可以增加粒子的多样性，加大算法跳出局部极小的几率，避免产生早熟收敛现象，提升全局寻优能力。

2 基于自适应粒子群优化(APSO)算法的图像匹配

2.1 模板相关匹配

在图像识别和处理方法中，模板相关匹配法被广泛应用于图像匹配，其计算简单、容易实现且抗干扰性能强。设基准图像S大小为M×N，模板T大小为X×Y，待匹配的目标子图记为Si,j，i,j表示目标子图左上角像素点在基准图S中的坐标，其中1≤i≤M-X+1,1≤j≤N-Y+1。

结合APSO算法的粒子化特点以及全局寻优特性，模板匹配问题可以转化为利用APSO算法搜索目标子图Si,j位置的最优解。在粒子位置和速度更新过程中，利用式(3)计算惯性权值ω，学习因子c1=c2=2。

选用平均绝对差(MAD)算法作为适应度评价函数，该算法耗时少且易实现，公式如下：

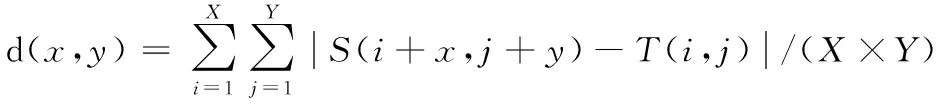
(5)

式(5)中，d(x,y)为相似性度量函数，表示偏移量为(x,y)时所对应的匹配度量值，其中1≤x≤M-X+1，1≤y≤N-Y+1。当d(x,y)取最小值时，能够得到最佳匹配位置(x,y)。

2.2 实验仿真

本文选取经典图像Lena作为实验仿真对象，其中Lena基准图像S大小为254×254，如图1(a)所示；模板T大小为64×76，如图1(b)所示。实验中选取粒子规模为50，最终的图像匹配结果如图1(c)所示。

图1 基于APSO算法的图像匹配结果

实验所用计算机配置如下：CPU：Intel Core i5-4590；主频：3.3GHz；内存：8G；仿真软件：MATLAB 7.0。

本文选取APSO算法中的迭代次数分别为20、30、40和50，并与基于灰度的MAD算法、归一化互相关(NCC)算法的运行结果进行对比，实验次数30次。实验结果如表1所示。

从表1对比结果可知，本文所设计的APSO算法匹配速度快，且表现出较好的匹配准确率，其他两种算法在匹配速度方面劣势明显，当匹配精度同时达到100%时，APSO算法平均运行时间是MAD算法的1/15左右、NCC算法的1/30左右。同时对于APSO算法，随着迭代次数的递增，匹配精度提高，但是算法的平均运行时间也相应增加。通过大量的实验分析发现，算法的迭代次数应选取适当，迭代次数过多会降低运算效率，若过少则会影响匹配精度；对于粒子数目的选取亦应适当，粒子数目的多少直接影响算法的全局寻优能力。

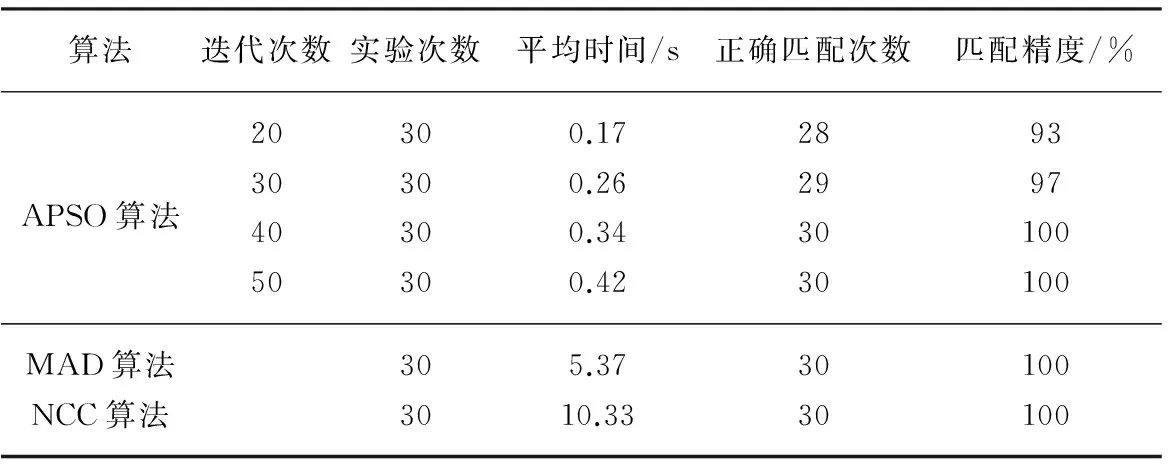
表1 APSO算法与MAD算法、NCC算法的匹配结果比较

为测试APSO算法的鲁棒性能，本文在Lena基准图像S中加入了Gaussian噪声(均值0，方差0.02)，如图2(a)所示。通过利用APSO算法进行图像匹配，可以实现匹配位置的准确定位。匹配结果如图2(c)所示。

图2 Gaussian噪声下的APSO算法匹配结果

在Gaussian噪声环境下，将APSO算法与MAD算法、NCC算法的运行结果进行对比，测试几种算法的鲁棒性能。其中，选取APSO算法的粒子规模为50，最大迭代次数为40，实验次数30次。结果如表2所示。

表2 加噪环境下几种算法的鲁棒性能比较

由表2可知，APSO算法在噪声环境下能够准确无误地找到匹配位置，抗干扰能力突出，具有强鲁棒性。同时在运行速度方面具有较大优势，匹配速度更快。

在无噪声环境下，本文对模板T的大小进行随机更改，并将APSO算法与MAD算法、NCC算法在平均运行时间方面进行比较。实验中选取APSO算法的粒子规模为50，最大迭代次数为40，实验次数为30。结果如表3所示。

表3 不同模板下几种算法的平均运行时间比较 s

算法模板T1/30×33模板T2/76×64模板T3/97×91APSO算法0.250.340.58MAD算法6.025.377.24NCC算法16.8510.3311.27

由表3可知，在不同模板大小下，APSO算法的平均运行时间均小于其他两种算法，匹配速度更快。同时，APSO算法的运算时间与模板大小成正比，模板越小，匹配速度越快，反之速度减慢；而另外两种算法在模板过大或过小的情况下，运行时间均会增加，相应降低了图像匹配过程。

3 结束语

本文通过对粒子群优化(PSO)算法的分析研究，提出了一种基于自适应粒子群优化(APSO)算法。实验证明该算法具有较好的收敛速度以及更高的收敛精度，能够跳出局部极小，避免早熟收敛现象，增强全局寻优能力，在图像匹配方面具有更好的匹配速度和匹配精度，且具有强鲁棒性，表现出较好的性能。算法后期将以参数优化、算法融合作为改进方向，同时将改进后的算法应用于其他图像处理技术之中。

[1]Guo X,Wang W.Image matching algorithm based on subdivision wavelet and local projection entropy[C]//The 6th World congress on Intelligent Control and Automation.Dalian China,2006:10380-10383

[2]伍庆华，王典洪，颜雪松．一种用于图像匹配的演化算法研究[J]．计算机工程与应用，2010，46(23)：181-184

[3]曹耀辉．一种图像高精度匹配算法[J]．计算机仿真，2009，26(9)：203-206

[4]罗钟铉，刘成明．灰度图像匹配的快速算法[J]．计算机辅助设计与图形学学报，2005，17(5)：966-970

[5]Chalermwat P,Ei G T,Le Moigne J.Two-phase genetic algorithm-based imageregistration on parrallel clusters[J].Journal of Future Generation Computing Systems,2001,17(3):467-476

[6]郑军，诸静．基于自适应遗传算法的图像匹配[J]．浙江大学学报:工学版，2003，37(6)：61-64

[7]鹿艳晶，马苗．基于灰色粒子群优化的快速图像匹配算法[J]．计算机工程与应用，2009，45(10)：157-167

[8]Garnier S,Gautrais J,Theraulaz G.The biological principles of swarm intelligence[J].Swarm Intelligence,2007(1):3-31

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2015.11.025

2015-08-01

宿州学院一般科研项目“瑞利衰落环境下的频谱检测方法研究”(2014yyb03)；宿州学院科研平台开发课题“基于可信计算的无线局域网安全体系结构的研究”(2014YKF44)。

冯浩(1983-)，河南安阳人，硕士，助教，主要研究方向:图像处理、智能算法。

TP391

A

1673-2006(2015)11-0098-04