Dirichlet空间DH上Toeplitz算子

戴星超

浙江师范大学数理与信息工程学院，浙江金华，321004

Dirichlet空间DH上Toeplitz算子

戴星超

浙江师范大学数理与信息工程学院，浙江金华，321004

Sobolev空间；Dirichlet空间；Toeplitz算子；交换性；有限秩；紧算子

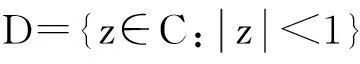
这里的偏导数是弱导数。这时，f在边界上有确定的属于L2(T)的迹[1]，则在Sobolev空间上定义如下范数：

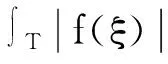
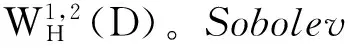
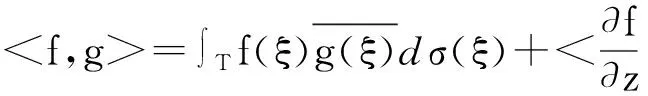
其中符号 <·,·>L2表示Hilbert空间L2(D,dA)中的内积。

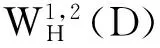
f(w)=,∀f∈DH

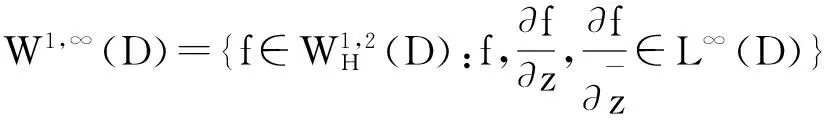
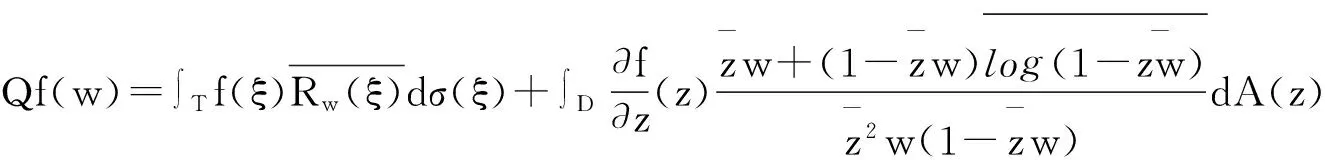
任给ψ∈W1,∞(D)，则在DH上以ψ为符号的Toeplitz算子定义为：

Tψf=Q(ψf),f∈DH

容易证明Tψ是DH上的有界线性算子。

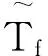
在经典Hardy空间H2(T)上，Brown和Halmos证明了Tf为紧算子当且仅当它是零算子[2]，但在H2(T)上不存在非平凡的紧算子，而在Bergman空间上却存在许多非平凡的紧Toepliz算子。2010年，于涛证明了Dirichlet空间上紧算子只能是零算子[8]。

1 Sobolev空间的直和分解

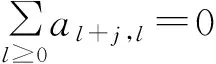
(1)当l+j=0时，上面等式变：

又因为

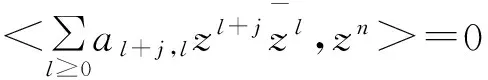
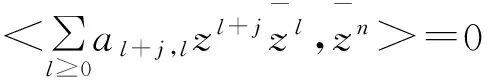
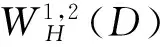
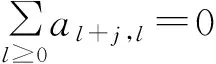
设f∈WH1,2(D)，记f在T上的迹为f|T。

定理1.1[8]设函数f∈WH1,2(D)，则下面成立：

(1)f∈A0当且仅当f|T=0；

(2)f∈A当且仅当f|T是常数。

定理1.2[8]设函数f∈W1,∞(D)，则fA0⊆A0。

2 主要结果和证明

引理2.1设ψi∈W1,∞(D),i=1,2,3,…,n,(ψi)|T表示ψi的迹，则对任意的f∈DH，有

证明：令P[ψ|T]表示ψ|T的Poisson延拓，则有：

设ψ∈W1,∞(D)，由定理1.2易知Tψ=TP[ψ|T]。以下设m≥0的一个固定整数，则：

TP[ψ|T](zm)(w)=Q(P[ψ|T]zm)(w)

=

=

现在令ψi∈W1,∞(D),i=1,2,3,…,n，显然有

Tψ1Tψ2Tψ3…Tψn(f)

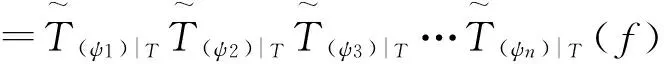
证明由引理2.1知显然成立。

定理2.3设φ,ψ∈W1,∞(D)，则在DH上TφTψ=TψTφ当且仅当下列条件的其中之一成立：

(1)φ,ψ∈A0⊕DH；

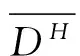
(3)存在不全为零的常数a,b∈C，使得aφ+bψ∈A。

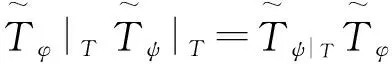
(1′)φ|T和ψ|T是解析的；

(2′)φ|T和ψ|T是共轭解析的；

(3′)存在不全为零的常数a,b∈C，使得aφ|T+bψ|T=0。

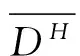
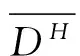
证明证明方法与定理2.3类似。

定理2.5设φ,ψ∈W1,∞(D)，则交换算子TφTψ-TψTφ有有限秩当且仅当下面条件的其中之一成立：

(a)存在一个解析的非零多项式p，使得pφ,pψ∈A0⊕DH；

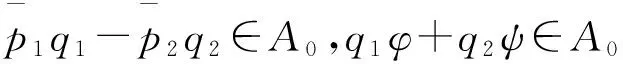
(a′)存在一个解析的非零多项式p，使得pφ|T和pψ|T是解析的；

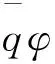
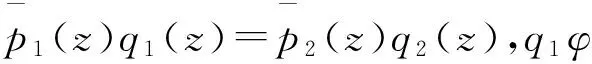
因为条件(a′),(b′),(c′)分别对应等价于条件(a),(b),(c)，所以定理是成立的。

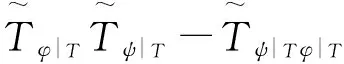
(i)在DH上Tψ=0；

(ii)Tψ在DH上是紧算子；

(iii)ψ∈A0。

Tψ为紧算子，则当j→∞，有：

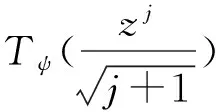
所以对所有的n,m,bn=am=0，从而ψh=0，故ψ=ψ0∈A0。

[1]AdamsR.SobolevSpace[M].NewYork:AcademicPress,1988:1-203

[2]BrownA,HalmosPR.AlgebraicpropertiesofToeplitzoperators[J].JReineAngewMath,1964,213:89-102

[3]AxlerS,Cuckovic.CommutingToeplitzoperatorswithharmonicsymbols[J].IntegralEquationsandOperatorTheory,1991,14(1):1-12

[4]DuistermaatJJ,LEEYJ.ToeplitzoperatorsontheDirichletspace[J].JournalofMathematicalAnalysisandApplications,2004,300(1):54-67

[5]陈泳，徐辉明，于涛．Dirichlet空间上Toeplitz算子的交换性(Ⅱ)[J]．数学年刊，2010，31A(6)：737-748

[6]LeeYJ.AlgebraicpropertiesofToeplitzoperatorsontheDirichletspace[J].JournalofMathematicalAnalysisandApplications, 2007,329(2):1316-1329

[7]ChenYong.Commutingtoeplitzoperatorsonthedirichletspace[J].JournalofMathematicalAnalysisandApplications,2009,357(1):214-224

[8]YuTao.Toeplitzoperatorsonthedirichletspace[J].IntegralEquationsandOperatorTheory,2010,67(2):163-170

[9]SheldonAxler.SunYungChangandDonaldSarason,ProductsofToeplitzoperators,IntegralEquationsOperatorTheory1[J].IntegralEquationsOperatorTheory,1978,1(3):285-309

[10]DingX,ZhengD.FiniterankcommutatorofToeplitzoperatorsorHankeloperators[J].HoustonJMath,2008,34:1099-1119

[11]YuTao.OperatorsontheorthogonalcomplementoftheDirichletspace[J].JournalofMathematicalAnalysisandApplications,2009,357(1):300-306

(责任编辑：汪材印)

Toeplitz Operators on the Dirichlet SpaceDH

DAI Xingchao

College of Mathematics,Physics and Information Engineering,Zhejiang Normal University, Jinhua Zhejiang 321004,China

Sobolev space；Dirichlet space；Toeplitz operator；commutativity；finite rank；compact operator

10.3969/j.issn.1673-2006.2015.11.024

2015-09-21

国家自然科学基金“多复变函数空间上的算子理论”(11271332)。

戴星超(1987-)，安徽宿州人，硕士研究生，主要研究方向：算子理论。

O177.1

A

1673-2006(2015)11-0094-04