基于空间仿射对应点列的双曲抛物面三维构建及分析
2012-04-18江晓红
江晓红, 宋 彦
(中国矿业大学,江苏 徐州 221116)
基于空间仿射对应点列的双曲抛物面三维构建及分析
江晓红, 宋 彦
(中国矿业大学,江苏 徐州 221116)
利用计算机3D软件构建基于空间仿射对应点列的双曲抛物面。对双曲抛物面进行不同方向的投射,可以准确得到双曲抛物面不同方位和角度的投影图。从这些投影图中,可以更直观、清楚的了解双曲抛物面的投影特点。使用多个不同位置的平面对双曲抛物面进行截切,并通过分析、观察截交线的变化趋势,得出几点规律性的结论。
仿射点列;3D造型;双曲抛物面;截交线
由空间解析几何可知,双曲抛物面属于二阶直纹曲面,它有两族直母线,每族直母线始终平行于各自的导平面[1-2]。从射影几何的角度看,双曲抛物面是由仿射点列对应点的连线包络成的二次曲面[3]。空间二仿射对应点列的度量性与仿射比 r,二线角 α和二线距 L有关,其中α为v1vi二交叉直线夹角,L为v1vi二交叉直线距离[4]。
在计算机虚拟三维空间中,根据上述概念及原理构建双曲抛物面,可以更方便和直观地了解双曲抛物面的投影特点及其截交线的变化规律。
1 仿射对应点列形成的双曲抛物面的三维构建及其投影特点
利用计算机三维CAD软件在虚拟三维空间中,建立位于两组任意位置不相交直线上的仿射对应点阵v1(Iv1, IIv1, Ⅲv1…)、v2(Iv2, IIv2, Ⅲv2…)、vi(Ivi, IIvi, Ⅲvi…)…以及u1(Iu1, IIu1, Ⅲu1…)、u2(Iu2, IIu2, Ⅲu2…)、uj(Iuj, IIuj, Ⅲuj…)…,得到两族直母线V、U,并由两族直母线V、U进行扫略,得到双曲抛物面A,如图1(a)。v1与vi两仿射对应点列仿射比r,二线角α和二线距L,如图1(b)所示。

图1 三维双曲抛物面及其投影
图1(b)是由双曲抛物面A得到的一组三面投影图。这里使同族各仿射对应点列水平投影同向,因此,可直接确定两个导平面的方向。令平行于V族母线的导平面为P、平行于U族母线的导平面为Q,导平面P、Q交线为N。导平面P、Q均垂直于H面,因此,H面投影中反映两导平面P、Q夹角θ的实形。导平面P、Q交线N为铅垂线。

图2 双曲抛物面投影的特殊形式
图3是由双曲抛物面A得到的又一组三面投

图3 双曲抛物面投影的一般形式
V面及W面投影中,V族及U族各仿射对应点列均不同向,V族及U族对应点连线的投影包络成抛物线。图1(b)中,双曲抛物面A的H 面投影为特殊形式,V面及W面投影为一般形式。
图2是由双曲抛物面A得到的另外一组三面投影图。这里使V族各仿射对应点列v1, v2, …, vi以及U族各仿射对应点列u1, u2, …, ui在H 面上投影分别同向,并使U同族各仿射对应点列u1, u2, …, ui平行于V面,导平面P为铅垂面、Q为正平面,两导平面P、Q夹角θ反映实形。V面投影为双曲抛物面投影的一般形式,但能真实反映各仿射对应点列u1, u2, …, ui两两之间的仿射比r和二线角α的大小。W面及H1面为双曲抛物面A投影的另一种特殊形式,其中U族各仿射对应点列u1, u2,…, ui彼此平行,而V族各仿射对应点列v1, v2, …, vi交于一点。影图,是双曲抛物面投影的一般形式。三面投影中,V族及U族各仿射对应点连线包络成抛物线。
从以上分析可以看出空间任意位置不相交的二仿射对应点列v1(Iv1,Ⅱv1,Ⅲv1…),vi(Ivi,Ⅱvi,Ⅲvi…)都可以通过投影变换得到其正投影[4]。由仿射对应点列v1, v2, …, vi及u1, u2, …, ui构成的双曲抛物面的投影特点:
1) 双曲抛物面 V族各仿射对应点列 v1, v2,…, vi及U族各仿射对应点列u1, u2, …, ui投影后仍为仿射对应点列,且对应关系不变。
2) 在一般情况下,双曲抛物面上的两族仿射对应点列的同名投影均不同向;两族仿射对应点列的投影不反映θ、α和L的真实大小;仿射对应点列v1, v2,…,vi及u1, u2,…, ui连线的投影包络成抛物线。如图1(b)中V、W面投影、图2中V面投影及图3所示。
3) 特殊情况下,双曲抛物面上的一族或两族仿射对应点列的同名投影同向。当一族仿射对应点列如u1, u2,…, ui在某一投影面上的投影同向时,该仿射对应点列间的距离L反映实长,而另一族仿射对应点列v1, v2,…, vi在该投影面上的投影则交于一点,如图2中W面及H1面投影所示。当两族仿射对应点列v1, v2,…,vi及u1, u2,…, ui在某一投影面上的投影分别同向时,可直接确定两个导平面P、Q的方向,导平面P、Q均垂直于该投影面,并反映其二面角θ的真实大小,如图1(b)及图2中H面投影所示。
4) 当双曲抛物面上的一族仿射对应点列平行于某一投影面时,该族所有仿射对应点列所构成的直母线在该投影面上的投影反映实长,其仿射对应点列的仿射比r和二线角α反映实际大小,仿射对应点列对应点连线的投影包络成抛物线。
从上面双曲抛物面造型及其投影图可以直观清楚的看出:双曲抛物面是由仿射点列对应点的连线包络成的二次直纹曲面,双曲抛物面有V、U两族直母线,每一族直母线都覆盖整个曲面,而且经过曲面上每一点有每一族唯一的一条直母线,同族每两条母线不共面,异族的两条母线共面;同族的一切直母线,平行于同一平面[1]。
2 双曲抛物面截交线的变化规律
双曲抛物面截交线的性质、形状随截平面位置的不同而不同。下面通过对三维双曲抛物面进行不同位置的截切,讨论其截平面位置与截交线的关系。
图4中,平面R平行于导平面Q,截切双曲抛物面得到U族中的一条直母线UR;同样,平面S平行于导平面P,截切双曲抛物面得到为V族中的一条直母线VS。

图4 截交线为一条直母线
图5中,正垂面R经过一条母线VR截切双曲抛物面,得到两条异族直母线VR、UR;同样,正垂面S经过一条母线US截切双曲抛物面,得到两条异族直母线VS、US。
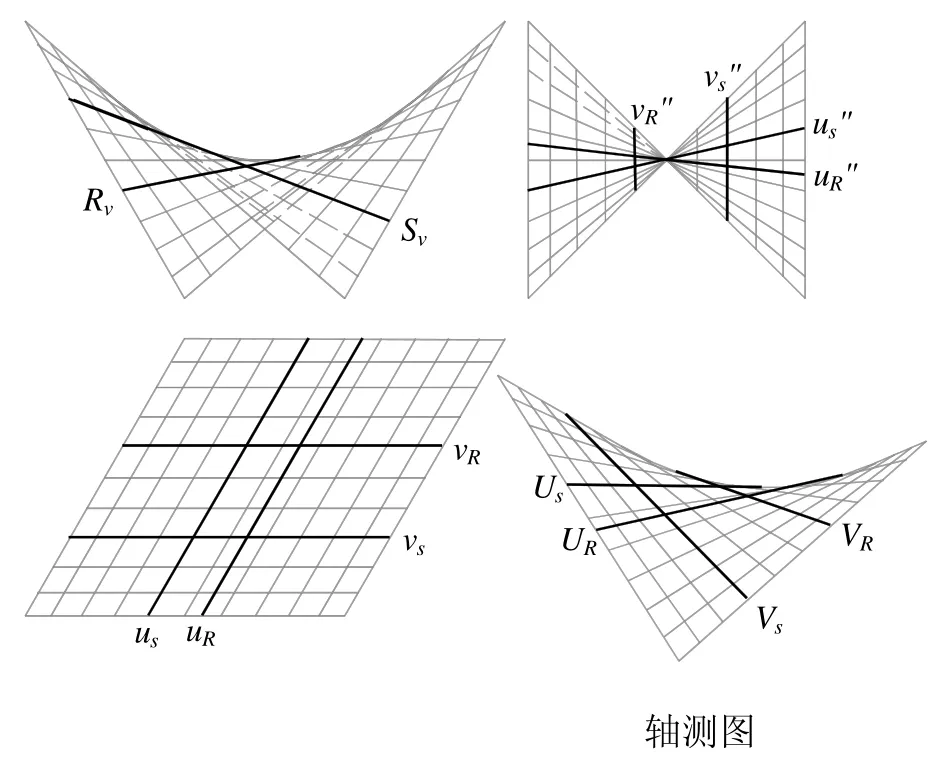
图5 截交线为一对异族母线
图6中,S平面由异族直母线VS和US构成,以S面作为分界面,用平行于S面的上下两组平面截切双曲抛物面,截交线为两族不同方向的双曲线,其渐近线方向相同,即与S面所截的两条直母线VS和US方向相同。VS和US的各面投影也是两族双曲线同名投影的渐近线。
图7中,两组平行于两导平面P及Q交线N、且与P及Q面均不平行的正平面及侧平面截切双曲抛物面,截交线为抛物线,其抛物线的轴线平行于两导平面P及Q的交线N。
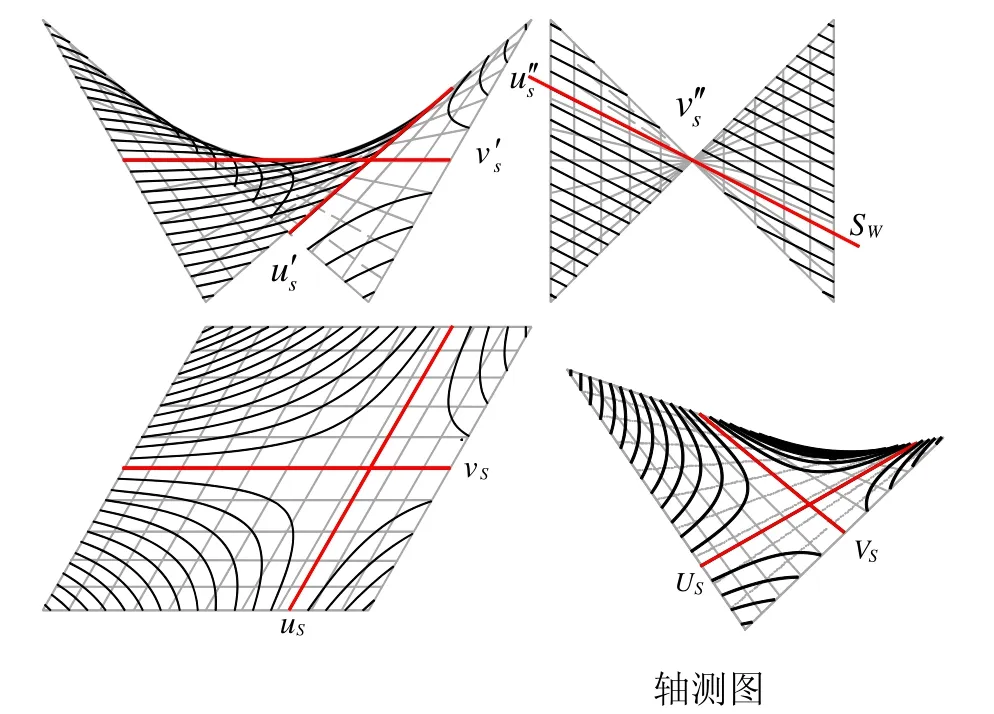
图6 截交线为二族双曲线

图7 截交线为抛物线
图8中,一组平面A、B和C平行于双曲抛物面两导平面P及Q的交线N(设N向上为正)、并且与Q的夹角大于0°且小于θ时,截得的抛物线顶点在下,开口朝上,即开口方向与N的正向同向;而当另一组平面 D、E、F等平行于两导平面P及Q的交线N、并且与Q的夹角大于θ并小于180°时,截得的抛物线顶点在上,开口朝下,即开口方向与N的正向反向。
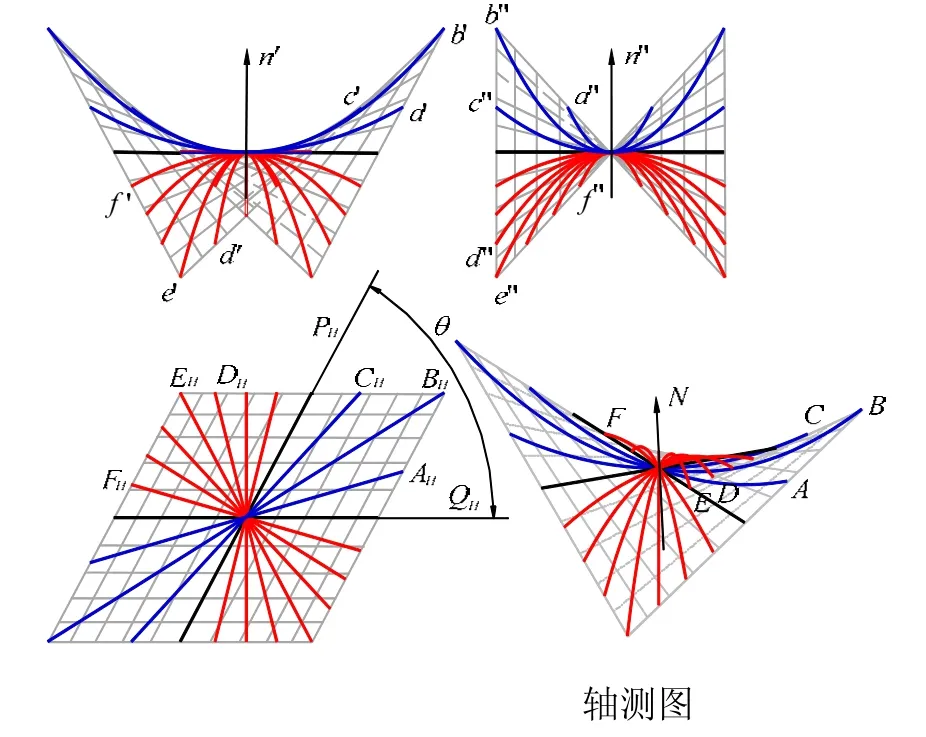
图8 抛物线的开口方向和其截平面与导平面的夹角有关
通过上面对三维双曲抛物面的空间以及二维投影分析可得出下面的结论:
1) 经过双曲抛物面一条母线,且不平行于导平面的每一个平面也必然经过属于另一族的一条母线。这样的平面截切双曲抛物面,截得两条异族直母线。
2) 当平面平行一条母线vm,且不平行于导平面时,也必然平行于属于另一族的一条母线un,这样的平面截切双曲抛物面,截交线为双曲线,其渐近线的方向即是母线vm及母线un的方向。这样一组平行的平面截切双曲抛物面,截得的双曲线具有相同方向的渐近线,与母线vm及母线un平行。
3) 平面在双曲抛物面上截得的每一对双曲线,其渐近线均平行于一对异族母线,这对异族母线构成的平面与该平面平行。
4) 当平面平行于两导平面P及Q的交线N、且与P及Q面均不平行时,截切双曲抛物面,截交线为抛物线,抛物线的轴线平行于两导平面P及Q的交线N。
5) 双曲抛物面上抛物线的开口方向和截平面与导平面P及Q的夹角θ有关,如图8。当截平面与导平面的夹角大于0°并小于θ时,抛物线的开口方向与N的正向同向;当截平面与导平面的夹角大于θ并小于180°时,抛物线的开口方向与N的正向反向。
3 结 束 语
利用计算机三维造型软件可以构建基于空间仿射对应点列的三维双曲抛物面。对三维双曲抛物面进行不同方向的投射,可以准确得到双曲抛物面不同方位和角度的投影图。从这些投影图中可以更直观、清楚的了解双曲抛物面的投影特点。使用多个不同位置的平面对三维双曲抛物面进行截切,并通过分析、观察截交线的变化趋势,得出几点规律性的结论。
[1] 南开大学数学系《空间解析几何引论》编写组编. 空间解析几何引论[M]. 北京: 人民教育出版社, 1978: 154-160.
[2] 何 斌, 陈锦昌, 王枫红. 建筑制图[M]. 北京: 高等教育出版社, 2010: 111-114.
[3] 刘阜平, 丁 勇. 二射影对应点列与二级曲线[J].山西矿业学院学报, 1996, 52(4): 354-358.
[4] 刘阜平, 丁 勇. 空间二仿射对应点列形成的双曲抛物面[J]. 工程图学学报, 2011, 32(6): 2-4.
The 3D modeling and analysis of hyperbolic paraboloid based on the spatial affine point ranges
Jiang Xiaohong, Song Yan
( China University of Mining and Technology, Xuzhou Jiangsu 221116, China )
This article constructs three-dimensional hyperbolic paraboloid based on spatial affine point ranges using the computer 3D software. From the projection in different directions on hyperbolic paraboloid,a series of projection drawing in different directions and angles of the hyperbolic paraboloid can be acquired. The characteristics of the projection drawing of the hyperbolic paraboloid are understood more directly and clearly from these projections. By using a number of planes of different locations to cut the hyperbolic paraboloid and by analyzing and observing the trend of intersection lines, several conclusions of regularity are obtained.
affine point ranges; 3D modeling; hyperbolic paraboloid; intersection line
O 185
A
2095-302X (2012)05-0024-04
2010-02-15;定稿日期:2012-04-10
江苏高校优势学科建设工程资助项目
江晓红(1958-),女,吉林长春人,教授,博士,主要研究方向为工程图学、计算机三维CAD。E-mail:xh.jiang@126.com
