人字形微型桩内力计算方法
2015-01-03施艳秋郑静吕昌明
施艳秋,郑静,吕昌明
(1.中国铁道科学研究院研究生部,北京100081;2.中铁西北科学研究院有限公司,甘肃兰州730000; 3.兰州交通大学,甘肃兰州730070)
人字形微型桩内力计算方法
施艳秋1,2,郑静2,吕昌明3
(1.中国铁道科学研究院研究生部,北京100081;2.中铁西北科学研究院有限公司,甘肃兰州730000; 3.兰州交通大学,甘肃兰州730070)
基于弹性地基梁的微型桩内力计算方法中有一种是假定上部为钢架,滑面处为固定支座,传递弯矩和剪力,滑面以下桩体按弹性地基梁法计算。本文所选微型桩同样采用组合结构计算,同时考虑滑面处变形协调,把弹性地基梁的位移和转角作为上部结构的支座位移,考虑位移对内力的影响。针对微型桩滑面处弯矩,基于FLAC3D程序,建立简化的微型桩数值计算模型,提取桩的内力并绘制弯矩图,数值模拟结果与考虑变形协调后的弯矩图更接近。
微型桩 内力分析 变形协调 数值模拟
微型桩组合结构作为边坡防护的一种轻型支挡结构,由于其施工安全便捷,对环境适应性强,因此在中型和小型坡体病害防治中应用较广。微型桩通常以组合结构出现,常用的排架微型桩组合是将一组一定间距的微型桩用顶梁连接起来共同受力,但因微型桩平行布置而受力较差。针对这种情况,研究提出了人字形微型桩新结构。人字形微型桩加固边坡类似于树根布置,同等条件下与排架微型桩比较,其结构整体性与抗弯性能较好,变形较小,承载能力较高。目前微型桩的理论研究落后于工程实践。在内力计算研究方面,冯君等[1]将微型桩体系和桩间岩土体视为桩—岩土体复合结构,建立了分析模型并加以计算。肖世国等[2]按弹性地基梁理论对微型桩滑面上下部分别用m,k法进行了计算分析,未考虑滑面处变形协调,认为可以忽略处理。肖维民[3]对微型桩加固顺层边坡进行研究,并建立了微型桩平面刚架受力模型。孙宏伟等[4]总结了微型桩组合结构布置形式,并按桩土作用原理在弹性地基梁理论基础上提出了组合结构的计算公式。前述理论计算中,结构上半部在滑面处视为固定端是不完全恰当的,微型桩作为一种柔性支护结构,桩体在滑面处变形较大,不能忽略处理。本文在考虑滑面处桩身变形协调的前提下,通过内力计算公式推导、实例计算与数值模拟对比分析,研究人字形微型桩的内力。
1 理论研究
微型桩结构采用倾角为α的人字形布置,桩顶到滑面处的距离为h1,滑面上部结构受到均布荷载q的作用,计算简图如图1所示。为方便理论推导做如下规定与假设:①人字形微型桩简化为滑面以上受矩形分布荷载的刚架,滑面以下为受横向变形约束的弹性地基梁;②考虑桩间土对力的传递,假定微型桩的前后桩横向受力条件相同,荷载大小成倍数关系;③桩和土体的变形均是线弹性的,满足小变形假设以及Winkler弹性地基梁假定[5];④不计桩体自重、桩底反力、桩与岩土间侧向摩擦力。第一步首先采用结构力学力法原理推导上部结构内力,求出滑面处弯矩和剪力。第二步根据弹性地基梁理论推导下部结构的内力计算公式,将第一步计算结果弯矩和剪力代入下部弹性地基梁公式,求出滑面处的位移和转角。第三步推导在支座位移条件下,上部结构的内力计算公式,将第二步计算结果位移和转角代入支座位移公式求出上部结构内力,并与外荷载作用下的结构内力进行叠加。

图1 上部结构简化
上部根据结构力学求解三次超静定[6],解出滑面处1#桩的弯矩和剪力

2#桩的弯矩和剪力

式中,n为推力传递系数,其余参数见图1。
滑面以下按初参数法计算桩身内力,局部弹性地基梁的基本微分方程为
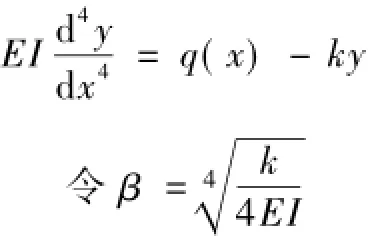
代入上方程,方程可改写为如下形式

方程的通解为
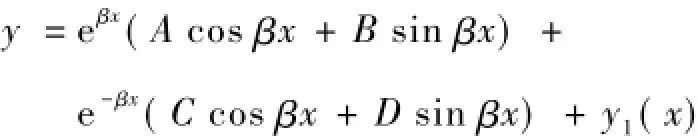
式中:EI为抗滑桩抗弯刚度,β是地基梁的特征系数,k为地基系数,y1(x)是方程的一个特解。无载段q(x)为0,特解y1(x)=0。初始截面的4个参数挠度、转角、弯矩和剪力就叫做初参数。初参数法的基本思路是把4个积分常数改用初参数表示,初参数方程如下
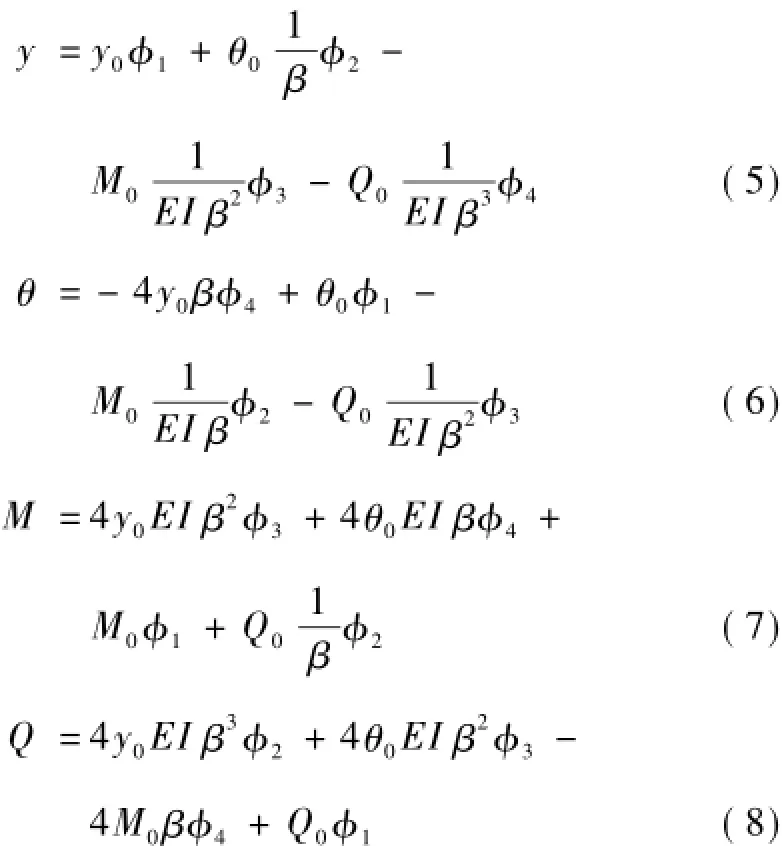
式中:φ1,φ2,φ3,φ4是为进一步简化公式定义的克雷洛夫函数,表达式为
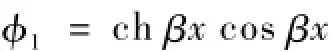

桩底的边界条件分为两种情况,第一种情况桩底为土层,按照自由端条件取弯矩和剪力为0;第二种情况,桩底嵌入岩层,按照固定端条件取位移和转角为0。选定桩底为土层,按滑面处桩身中心为坐标起点x=0,沿桩身中心向下为x轴正方向,则桩底端点边界条件为

代入初参数方程(7)和(8),联立两方程,令φi(βl)=φil,可解得滑面处桩身挠度y0和转角θ0为
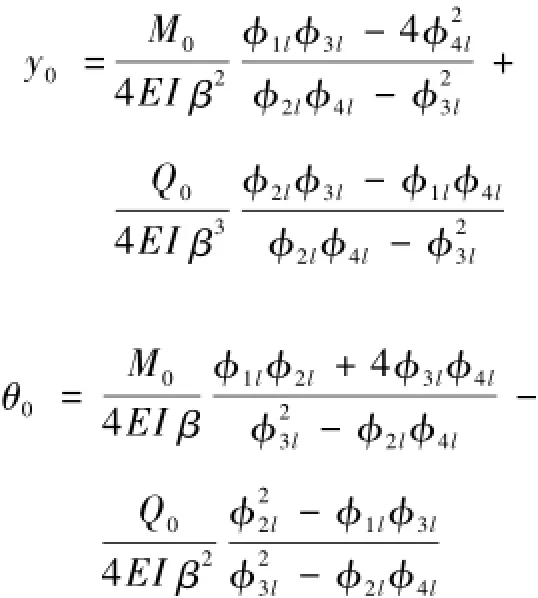
将第一步根据上部结构求出的1#桩和2#桩滑面处的弯矩和剪力,作为初参数M0和Q0代入求出其余两个初参数y0,θ0,代入初参数方程(5)~(8)就可以得到滑面以下任意桩长处的挠度、转角、弯矩和剪力。再推导支座位移条件下结构的内力:对人字形刚架超静定结构进行支座约束解除,代之以未知力X1(1#桩支座水平力向左)、X2(1#桩支座弯矩逆时针)、X3(2#桩支座弯矩顺时针),形成基本体系。设y1x,θ1表示1#桩支座的水平方向位移和转角,方向与未知力相同,y1y表示1#桩支座竖向位移,方向向下;设y2x,θ2表示2#桩支座的水平方向位移和转角,水平位移方向与支座反力相同,转角方向与未知力X3方向相同,y2y表示2#桩支座竖向位移,方向向下。则力法补充位移方程可以写为下式。

式中,Δ1c,Δ2c,Δ3c则分别代表基本结构上由于支座位移移动所引起的沿X1,X2,X3方向的位移。具体为
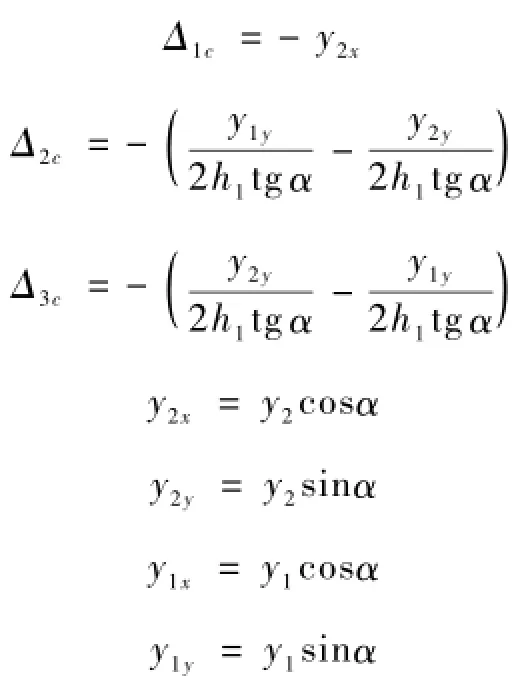
式中,y1,y2是根据弹性地基梁计算求出的桩顶挠度。基本结构在支座位移条件下补充位移方程如下

经过消元和回代,得到方程组的解
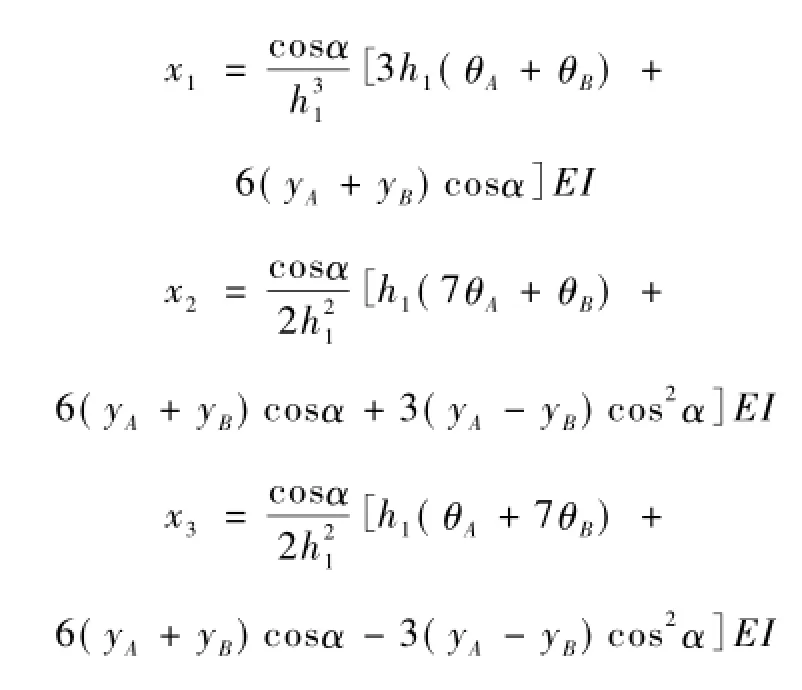
将支座反力转化为滑面处桩上的剪力和弯矩

将支座位移条件下结构内力与荷载作用下结构内力叠加,得到协调变形后的内力图。
2 实例分析
实际边坡作用在桩上的推力复杂,现简化桩后荷载为矩形分布[7],具体参数设置如表1所示。代入理论推导公式求出上部结构内力,再将滑面处弯矩和剪力代入下部弹性地基梁,应用初参数法计算得到的滑面处位移作为支座位移施加到上部结构。再进一步计算由此产生的上半部分桩体内力,将其与之前外荷载作用下桩体内力叠加得到考虑滑面处桩体位移后的上部结构内力。经调整后的内力值理论上更趋近于真实结构内力,将其代入下部结构,重复初参数法,可再一次得到滑面处的桩体位移,再计算下半部分内力和位移。比较前后两次内力的差值,若其满足精度要求,即可停止计算,否则继续迭代计算,直到满足精度要求为止。根据弹性地基梁理论,滑面以下按初参数法计算时,滑面处按自由端处理计算出的位移和转角比实际值大,应该折减后再作为支座位移代入上部结构。折减系数根据具体参数确定,保证支座位移对上部结构弯矩的影响不大于荷载对结构弯矩的影响,经有限次循环内力差值满足精度要求为止,这一过程可以编程来实现。本次计算采用C语言编程,运用双重循环首先确定满足要求的折减系数,再输出有限次循环后的弯矩和剪力。

表1 参数设置
调整位移前后A桩和B桩的内力见图2和图3。

图2 1#桩弯矩

图3 2#桩弯矩
从理论推导结果可以看出:①1#桩考虑滑面位移时的弯矩值比不考虑位移时减小81%,桩身弯矩考虑位移后明显减小,现场试验结果1#桩滑面处弯矩趋近于0,若不考虑变形协调理论计算与现场试验相差较大。人字形结构有倾角,协调变形后部分剪力转化为轴力,会使弯矩和剪力减小。②2#桩顶点处弯矩值增大,桩身整体弯矩值呈减小趋势,考虑支座位移时相当于放松滑面处约束条件,允许滑面处发生微小位移,桩身的弯矩将减小,上半部结构作为钢架考虑,变形对钢架内力影响较大,刚节点处的内力增大。
3 数值模拟
理论计算受假定条件限制,数值模拟可以将多种因素同时考虑到模型中且计算方便,在工程领域应用越来越多[8]。建立FLAC3D有限差分数值模拟,计算模型见图4。
图4 微型桩模型
模型分为上下两部分,上部为滑坡体,下部为稳定土层,滑面以上桩长2 m,滑面以下桩长4 m。具体参数设置如表2所示。约束稳定土层底部X,Y和Z三个方向位移,其他边界约束X和Y方向位移,土体采用Mohr-Coulomb弹塑性模型,微型桩采用桩结构单元模拟,每根桩由30个子单元构成,两根桩顶部刚结。为使数值模拟与理论推导具有可比性,要控制施加到桩上力的分布形式与大小,在右侧桩滑面以上施加与理论推导相同的均布力。

表2 土体和桩体参数
微型桩半径取0.15 m,计算后提取桩单元的弯矩值并绘出弯矩图,数值模拟结果与理论计算对比分析。弯矩图见图5和图6。
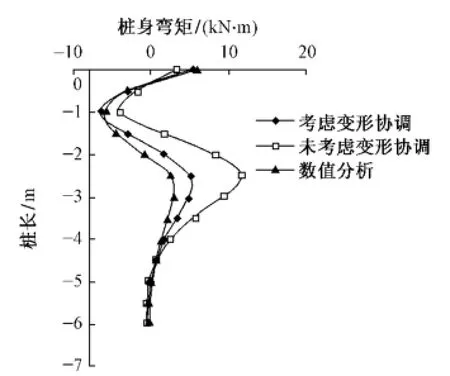
图5 1#桩弯矩

图6 2#桩弯矩
1)1#桩数值模拟弯矩图和调整位移后的弯矩图变形趋势更接近,数值模拟比理论推导结果略小,理论计算假定推力直接作用在刚架上与实际情况相差较大,数值模拟中土体摩擦力要消耗一部分推力。
2)2#桩数值模拟结果比协调变形后的弯矩值大,理论推导时2#桩的力是通过刚节点传过去的,数值模拟除了顶部刚节点传递力还通过土体变形传递一部分力。
4 结论
1)人字形新结构的理论推导,采用上部结构简化为刚架,下部采用弹性地基梁理论,并考虑了滑面处的位移。推导了相应计算公式,并代入具体参数,分析了支座位移对弯矩的影响。
2)建立简化数值模型,1#桩弯矩图与考虑变形协调后的弯矩图变形趋势一致,2#桩比理论计算结果大,数值模拟考虑了桩间土的影响,理论计算未考虑。
3)人字形新结构的理论计算方法目前研究较少,本文对新结构内力的理论研究和数值模拟,可给微型桩的内力理论分析提供参考。
[1]冯君,周德培,江南,等.微型桩体系加固顺层岩质边坡的内力计算模式[J].岩石力学与工程学报,2006,25(2):284-288.
[2]肖世国,鲜飞,王唤龙.一种微型桩组合抗滑结构内力分析方法[J].岩土力学,2010,31(8):2553-2560.
[3]肖维民.微型桩结构体系抗滑机理研究[D].成都:西南交通大学,2005.
[4]孙宏伟.刚性帽梁微型桩组合结构内力分析[D].成都:西南交通大学,2007.
[5]龙驭球.弹性地基梁的计算[M].北京:高等教育出版社,1981.
[6]李廉锟.结构力学[M].4版.北京:高等教育出版社,2004.
[7]刘凯,刘小丽,苏媛媛.微型抗滑桩的应用发展研究现状[J].岩土力学,2008,28(1):675-678.
[8]陈正,梅岭,梅国雄.柔性微型桩水平承载力数值模拟[J].岩土力学,2011,32(7):2219-2224.
Calculation method of internal forces in herringbone micropile
SHI Yanqiu1,2,ZHENG Jing2,LV Changming3
(1.Postgraduate Department,China Academy of Railway Sciences,Beijing 100081,China;2.Northwest Research Institute Co.Ltd of CREC,Lanzhou Gansu 730000,China;3.Lanzhou Jiaotong University,Lanzhou Gansu 730070,China)
Among existing calculation methods for micropiles internal force,the upper structure was assumed as a steel frame and the sliding surface as a fixed support transfering moment and shear while the lower structure as an elastic foundation beam.In this paper,the selected micropiles were calculated as a composite structure.T he deformation coordination at the sliding surface was considered,and the displacement and the rotation of the lower structure were used as those of the bearings for the upper structure.T he effect of the displacement on the internal force was studied.Based on the FLAC3D program,a simplified model was established to simulate the micropiles. T he internal force and the moment distribution were obtained with this model.W ith consideration of the deformation coordination at the sliding surface,the results were more closed to the results of numerical simulation.
M icropiles;Analysis of internal force;Deformation coordination;Numerical simulation
U213.1+52.1
A
10.3969/j.issn.1003-1995.2015.05.28
1003-1995(2015)05-0113-05
(责任审编赵其文)
2014-06-23;
2015-02-26
科研院所技术开发研究专项资金项目(20091EG123201)
施艳秋(1989—),女,甘肃兰州人,硕士研究生。
