基于高斯分布判决的SAR原始数据压缩方法

刘娟妮，周 诠

(西安空间无线电技术研究所空间微波技术国家级重点实验室， 西安710100)

0 引言

合成孔径雷达(Synthetic Aperture Radar，SAR)是一种全天候、全天时的现代高分辨率微波成像雷达，在军事和民用领域获得越来越多的重视和应用。随着SAR技术向多频段、多极化，超高分辨率以及多种工作模式方向发展，SAR原始数据量急剧增加，然而星载存储设备容量和数据传输带宽有限。因此，迫切需要结合星载SAR数据特性设计合理的压缩算法，解决数据存储和传输的问题。

分块自适应量化(Block Adaptive Quantization，BAQ［1］)算法根据SAR原始数据在距离向和方位向都是方差缓变的零均值高斯分布信号这一特性，将原始数据沿方位向和距离向分成若干小块(如32×32)，使小块数据的动态范围小于整个数据块的动态范围，再对每个数据块进行归一化处理，利用标准高斯信号的最优量化器Lloyd-Max［2］实现整个数据块的自适应量化，达到数据压缩的目的。由于其在压缩性能与硬件实现复杂度之间的良好折中，成为SAR原始数据压缩算法事实上的标准。由于受BAQ算法思想的影响，陆续出现了一系列BAQ的变异和改进算法。这些算法包括BFPQ 算法［3］，BAVQ 算法［4］，DCT-BAQ 算法［5］和 DWT算法［6］等，还有人把压缩感知引入SAR原始数据的压缩［7］。虽然这些改进方法在性能上优于BAQ，但是其复杂的计算过程阻碍了它们的实际应用，目前只有BFPQ和BAQ算法应用到实际的SAR系统中。

BAQ算法应用的前提条件是分块SAR原始数据用方差归一化后符合标准高斯分布，这个条件在大多数情况下是成立的。但是SAR成像场景变化复杂，不同地物的后向散射系数区别较大，有一些场景如海洋等，只有很少散射体，其回波信号的概率密度函数会偏离高斯分布。因此，再用Lloyd-Max量化器进行数据量化压缩就会造成较大的偏差。另外，SAR原始数据是回波信号经A/D量化得到的，由于SAR回波信号较大的动态范围在进行A/D量化时会在信号两端产生截断误差，其统计特征也会偏离高斯分布。对于这类特殊的数据块，很难找到一个合适的信源概率模型来模拟，因此应使用特殊的方法进行压缩。

文献［8］利用模糊逻辑判决法判断SAR数据块与高斯分布的偏离程度，该方法实现复杂且对硬件改动较大。文献［9］通过统计不同数据块在各区间内的概率分布给出经验公式，用来计算判断数据块是否符合高斯分布的阈值，对满足标准高斯分布的数据块进行标量量化，即BAQ;不满足的数据块进行矢量量化(VQ)。文献［9］的方法在性能上较BAQ有所提高，这说明对SAR数据概率分布进行预先判断，并分类进行压缩处理具有一定的意义。

因此，本文提出一种借助几何分析判断SAR数据是否符合标准高斯分布的新方法，并将其应用于SAR原始数据压缩。该方法将标准高斯曲线用等面积的三角形替代，计算出二者的交点坐标，并对各交点范围内二者的积分值进行比较，得到三个判决条件。当SAR数据的分布规律满足这些条件时，判断其为标准高斯分布并进行BAQ压缩，而不满足的数据采用文献［9］的矢量量化压缩方法。

1 算法原理及实现过程

1.1 高斯特性判断

根据中心极限定理，SAR原始回波的实部和虚部分别服从均值为零的高斯分布，在进行BAQ压缩时用数据块的方差对其进行了归一化，这样数据就为标准高斯分布，因此下面给出标准高斯分布的判决条件。

均值为零的标准高斯分布概率密度函数为

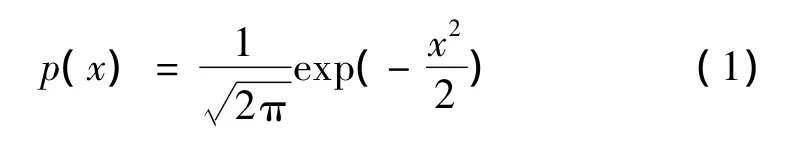
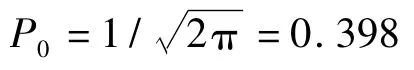
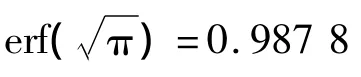
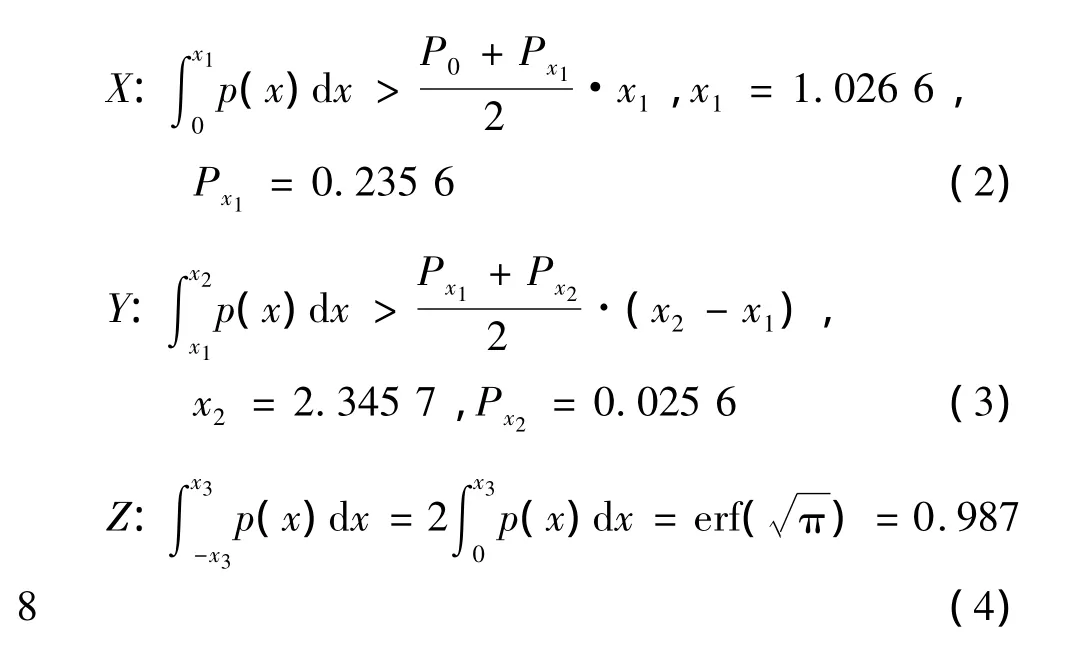
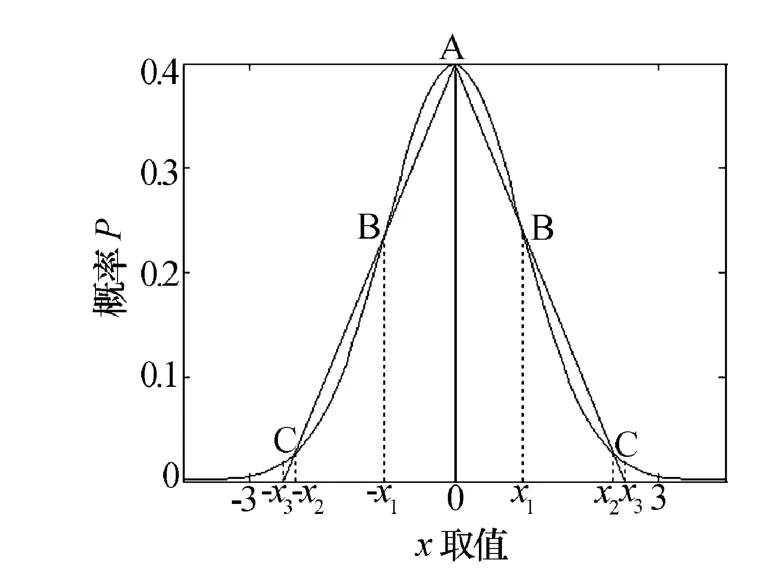
图1 标准高斯曲线与等面积三角形关系示意图

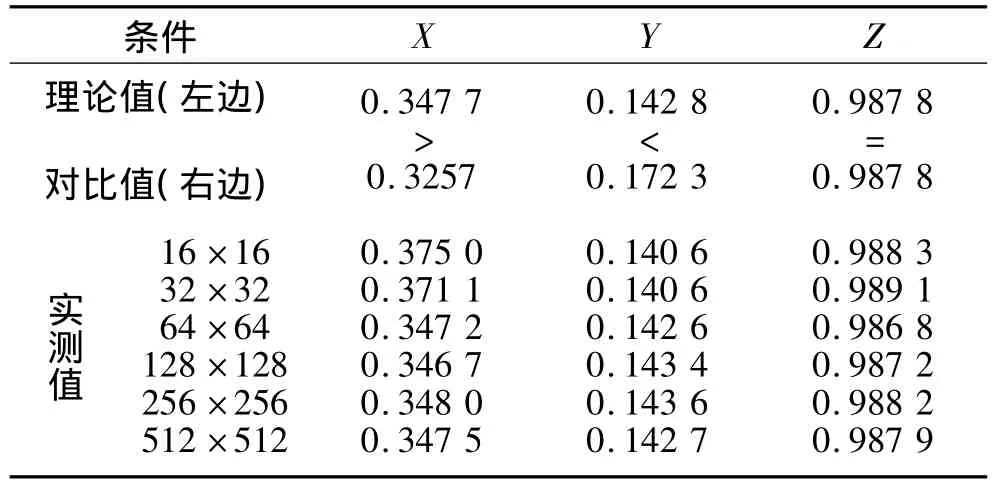
表1 仿真标准高斯数据的实验结果

可以看出，对于不同大小的数据块，实测的概率分布积分值与对比值相比，均满足条件X，Y中的不等式要求，条件Z的误差也在1%内，并且数据块大小不影响判断结果，只是随着数据块的增大，仿真数据的概率分布积分值更接近理论值。

同样，对真实SAR数据也进行了实验，数据分块大小为32×32，选择其中两个数据块的判断结果进行展示，它们的概率分布如图2所示。其中，图2a)对应的SAR数据经判断后三个条件均满足，可以认为符合标准高斯分布，并且从其概率分布图也可得出相同结论;而图2b)对应的SAR数据仅满足条件Z，所以判断为不符合标准高斯分布，其概率分布图已经偏离高斯分布，从而验证了判断的正确性。

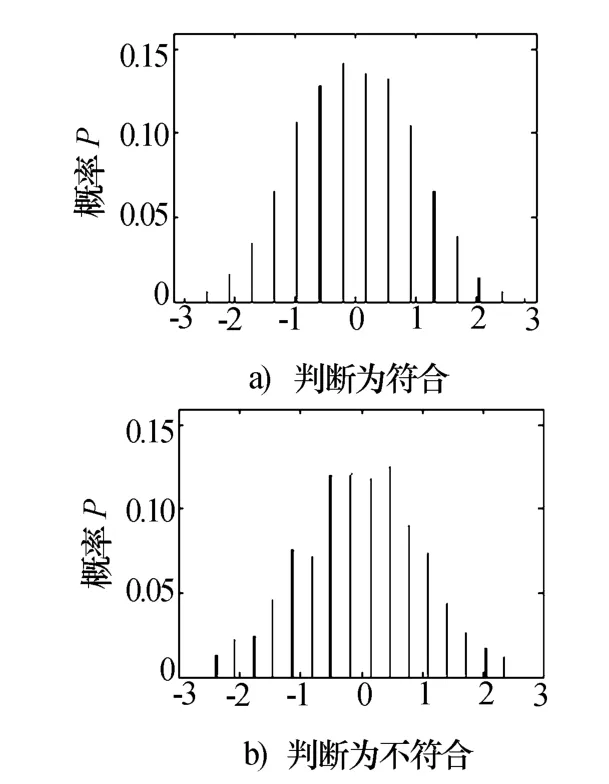
图2 真实SAR数据的概率分布

1.2 实现过程

下面具体说明算法的实现过程，图3为流程图。首先将SAR数据分块并归一化，然后利用三个条件判断数据块是否符合标准高斯分布，最后根据判断结果分别使用不同方法进行压缩。详细过程如下:

(1)将SAR原始数据分块，大小为32×32，估算各块方差并进行归一化;

(2)根据式(2)～式(4)判断三个条件是否成立，当三个条件都满足时认为数据符合标准高斯分布，否则不符合标准高斯分布;

(3)当数据符合标准高斯分布时，使用最优量化器Llyod-Max进行量化，即BAQ压缩方法;当数据不符合标准高斯分布时，对数据进行矢量量化压缩。

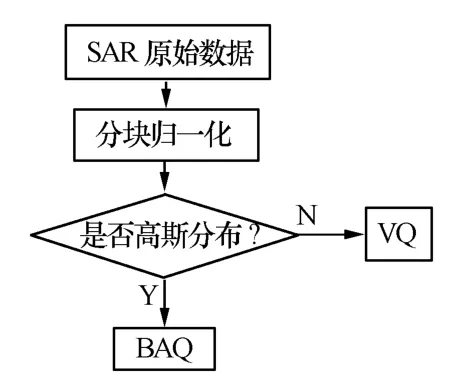
图3 算法实现流程图

2 实验结果与数据分析

本文采用文献［10］附带光盘的RadarSat-1温哥华数据进行仿真实验。选取其中图像内容较为丰富的2 048×1 536大小的回波数据作为实验数据。该实验平台为Matlab R2011a，主频为2.50 GHz，内存大小为2 GB。由于BAQ算法是目前比较成熟的SAR原始数据压缩算法，因此将本文算法结果与BAQ结果作比较。另外，为了说明本文方法在判断高斯分布偏离度的优势，将文献［9］高斯判断方法和本文算法也进行了比较。

2.1 压缩性能比较

表2～表4是3种算法在不同比特率时性能参数比较结果。评价采用数据域和图像域不同指标［11］，其中参数NMSE为归一化均方误差、SNR为信噪比、PSNR为峰值信噪比、MPE为平均相位误差、K为逼真度，ρ为相关系数。这些参数从不同方面反映了压缩算法的性能。图4给出了原始数据(RD)成像和本文方法在不同压缩比时数据成像的结果，可以看出，压缩数据重建图像基本保持了原始数据成像的细节部分，当量化为1bit时，仍然能够区分图像中的机场和河流。

表2 1bit压缩性能比较

表3 2bit压缩性能比较

表4 3bit压缩性能比较

从表2～表4中可以看出，相同比特率时，对于不同指标(MPE除外)，本文方法在三者中均最优，文献［9］的方法次之，BAQ最差。当量化比特数分别为1 bit，2 bit，3 bit时，和文献［9］方法相比，本文方法的数据域信噪比分别高出0.42 dB，0.67 dB，1.02 dB，图像域信噪比分别高出0.21 dB，0.59 dB，0.90 dB。这说明本文方法在判断数据是否满足高斯分布时更准确。另外，经过分析可以知道，判断为非高斯的SAR数据进行矢量量化能够获得比BAQ更好的压缩效果，所以对SAR数据预先进行概率分布判断具有实际意义。

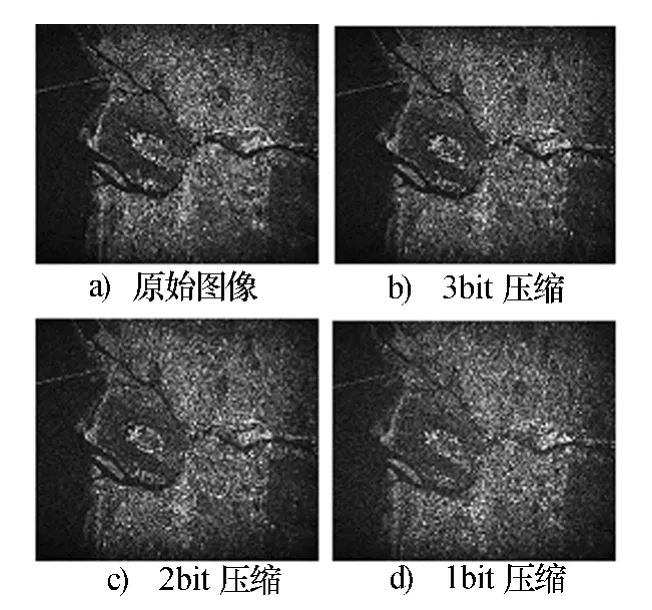
图4 压缩成像比较

值得注意的是，文献［9］通过对SAR数据块的概率分布进行统计，指出数据块落入区间［-1，1］内的概率差异较大，可以反映数据块与标准高斯分布的偏离程度，这个判断方法和本文给出的条件X思想类似。由于高斯曲线是关于y轴对称的，所以只需判断大于零的部分。本文通过等面积三角形近似高斯曲线，在条件X中，对区间［0，x1］内的高斯曲线和线段AB进行积分，比较二者的大小，来判断数据是否符合标准高斯分布。实际也是通过比较它们的概率分布进行判断的，而本文给出的区间端点x1=1.026 6，非常接近1，因此可以认为文献［9］的判断方法与本文条件X等价。另外，本文的条件Y和Z对高斯曲线在区间［x1，x2］和［-x3，x3］的概率分布也进行了判断。相比文献［9］的方法，本文的判断条件对区间划分更细，更准确。

2.2 计算复杂度比较

计算复杂度可以用运行时间来衡量。表5是使用BAQ算法、文献［9］算法和本文算法进行不同比特率压缩时所用时间(单位:s)的对比结果。待压缩的SAR原始数据大小为1 536×1 536，压缩比特率为1 bit，2 bit和3 bit时对应的VQ码书大小分别为8，64和512。

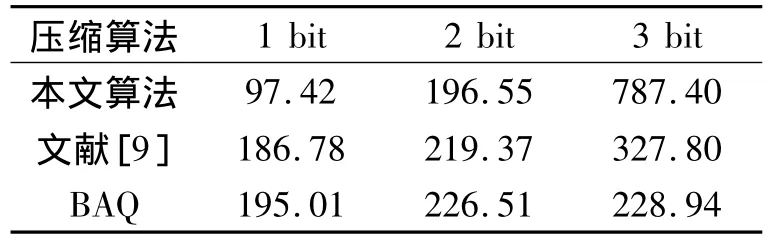
表5 运行时间比较

从表5中可以看出，随着压缩比特率的增加，三种算法的运行时间均呈递增趋势，且本文算法增加最明显，文献［9］次之，BAQ变化最小。这是因为随着比特率的增加，VQ码书大小呈指数增长，所以本文算法和文献［9］算法运行时间增加明显;另外，本文判断数据是否符合高斯分布的条件相比文献［9］更加准确，所以原始数据被判断为非高斯的比例增加，也就是说进行VQ压缩的数据块比例增加，因而运行时间会明显增加。然而，在压缩比特率为1 bit和2 bit时，本文算法运行时间最少，文献［9］次之，BAQ时间最长，这是由于此时VQ的码书很小，数据块进行VQ压缩比BAQ压缩时间短。

在实际工程中，可以根据具体的系统要求及硬件条件，将以上三种算法应用于SAR原始数据压缩中。

3 结束语

本文针对SAR数据概率密度函数偏离高斯分布时BAQ压缩算法性能下降的问题，提出一种借助几何关系判断SAR数据是否符合标准高斯分布的方法，并针对判断结果采用不同方法进行量化。通过一组实测SAR原始数据的仿真实验发现，在不同压缩比时，本文提出的SAR数据压缩方法性能均优于BAQ方法和文献［9］的方法，这说明本文判断高斯分布的条件更准确，对SAR数据压缩性能的改善具有一定的积极作用。

［1］Kwok R ，Johnson W T K.Block adaptive quantization of Magellan SAR data［J］.IEEE Transactions on Geoscience and Remote Sensing，1989，27(4):375-383.

［2］Max J.Quantizing for minimum distortion［J］.IRE Transactions on Information Theory，1960，6(1):7-12.

［3］Huneycutt B L.Spaceborne imaging radar-C instrument［J］.IEEE Transactions on Geoscience and Remote Sensing，1989，27(2):164-169.

［4］Moreira A，Blaser F.Fusion of block adaptive and vector quantizer for efficient SAR data compression［C］//International Geoscience and Remote Sensing Symposium.Tokyo，Japan:IEEE Press，1993，4:1583-1585.

［5］潘志刚，王岩飞.基于DCT的分块自适应量化算法及其用于SAR原始数据压缩［J］.电子与信息学报，2007，29(8):1784-1788.Pan Zhigang，Wang Yanfei.A compression algorithm for SAR raw data based on the combination of discrete cosine transform and block-adaptive quantization［J］.Journal of Electronics&Information Technology，2007，29(8):1784-1788.

［6］潘志刚，王岩飞.一种基于小波变换的高倍数SAR原始数据压缩算法［J］.电子与信息学报，2006，28(10):1798-1801.Pan Zhigang，Wang Yanfei.A wavelet-based algorithm for SAR raw data compression［J］.Journal of Electronics&Information Technology，2006，28(10):1798-1801.

［7］陈一畅，张 群，朱丽莉，等.基于压缩感知和矢量量化的SAR数据级联压缩方法［J］.现代雷达，2013，35(10):36-40.Chen Yichang，Zhang Qun，Zhu Lili，et al.A cascade compress method of SAR data based on compressed sensing and vector quantization［J］.Modern Radar，2013，35(10):36-40.

［8］Benz U C.A fuzzy block adaptive quantizer(FBAQ)for synthetic aperture radar［C］//3rd IEEE Conference on Fuzzy Systems.Orlando，USA:IEEE Press，1994:1006-1011.

［9］曾尚春，朱兆达.块自适应标量-矢量量化算法压缩SAR原始数据［J］.中国图象图形学报，2007，12(8):1349-1353.Zeng Shangchun，Zhu Zhaoda.Block adaptive scalar-vector quantization for SAR raw data compression［J］.Journal of Image and Graphics，2007，12(8):1349-1353.

［10］Cumming I G，Wong F H.Digital processing of synthetic aperture radar data:algorithms and implementation［M］.Norwood:Artech House，2005.

［11］ 宋鸿梅，王岩飞，潘志刚.基于DCT-TCQ的SAR原始数据压缩算法［J］.电子与信息学报，2010，32(5):1040-1044.Song Hongmei，Wang Yanfei，Pan Zhigang.DCT-TCQ based SAR raw data compression algorithm［J］.Journal of Electronics&Information Technology，2010，32(5):1040-1044.