工业机器人零位标定点约束分布研究

周 祥，杜姗姗

（南京理工大学计算机科学与工程学院，南京210094）

1 概述

工业机器人的应用越来越广泛。然而现今的机器人的重复定位精度高而绝对定位精度低，为了满足更多复杂任务的工作需求，标定机器人的准确参数变得尤为重要［1］。

机器人标定就是采用测量手段或者基于运动学模型的参数识别方法辨识出机器人模型的准确参数，从而提高机器人绝对精度的过程［2］。标定可以细分为参数标定、自标定以及正标定和逆标定等关键标定技术［3］。参数标定是获得运动学模型的一种相对有效且经济的标定方法［4－6］。其中零位标定属于参数的一种，是提高机器人定位精度最重要的一种标定方法［7］。

本文研究基于点约束的标定方法。在机器末端固定激光器，在机器人工作空间内放置一个位置传感器位置敏感检测器（Position Sensitive Detector，PSD），使激光以多个位姿定位到位置传感器的中心，实现点约束。单点约束要求激光线以多个姿态近似垂直投射在PSD表面，激光线的倾斜照射可能带来一定误差。另一方面机器人的标定系统中，可能存在其他系统误差，如杆件参数误差。基于点约束，本文提出多点约束进行标定，将PSD装置放置在机器人可达空间的多个位置，在每一位置上进行少量次数的激光定位，实现多点约束。通过仿真和实验，对比空间PSD多点分布与PSD单点约束的标定效果。

2 机器人模型

2．1 DH 模型

为了对机器人进行标定，首先要建立机器人的运动学模型，DH模型是应用最广泛的一种机器人建模模型，DH模型可以唯一地描述机器人运动链的结构［8］。DH 模型用αi，θi，ai，di这4个参数来描述机器人的连杆坐标系，对于旋转关节，θi是关节变量，其余3个参数是机器人连杆机构固有几何参数。其他3个参数分别为杆件长度ai、杆件扭角αi以及关节平移量di。利用DH模型进行机器人建模。建立轴i－1与轴i之间的齐次变换矩阵如下：

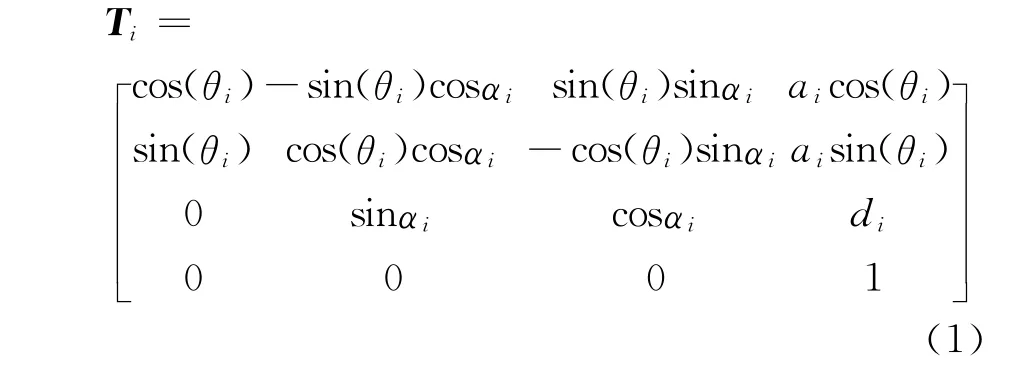
则六自由度工业机器人从机器人基坐标到机器人末端坐标系的变换矩阵可得如下：

2．2 零位误差模型的建立

用δi表示第i个关节的零位误差值，轴与轴之间的变换关系建立之后，结合零位误差值，重新建立带误差的DH模型，相应的齐次变换矩阵如下：

3 标定原理

3．1 约束模型

在之前的研究中，主要采用单点约束模型［9－10］。机器人末端执行器上固定激光器，当PSD位置固定不变时控制机器人使激光线近似垂直投射到PSD中心点。多次调整机器人位姿，进行激光定位，使多条激光线交于同一点，即PSD中心点，实现单点约束，单点约束的原理如图1所示。

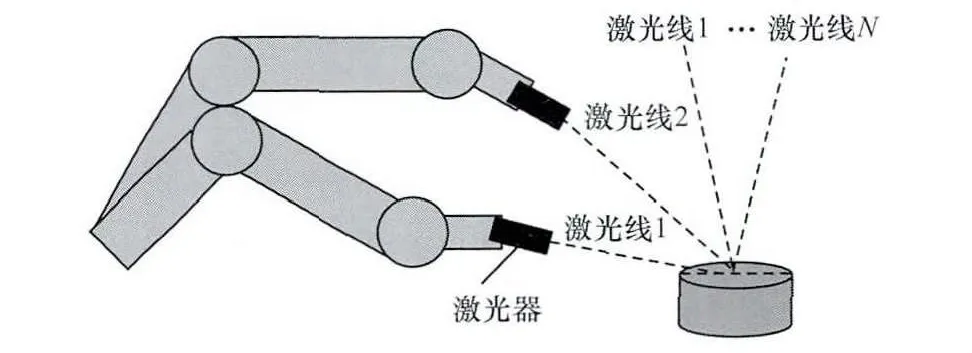
图1 单点约束标定原理

机器人标定系统中可能存在其他系统误差，如DH模型的误差以及激光定位时的定位误差等，本文提出用多点约束进行标定的方法，主要思想是在机器人的工作空间内，多个位置内放置PSD，每个位置上进行少量激光定位，最终多个位置上均实现点约束，标定原理如图2所示。

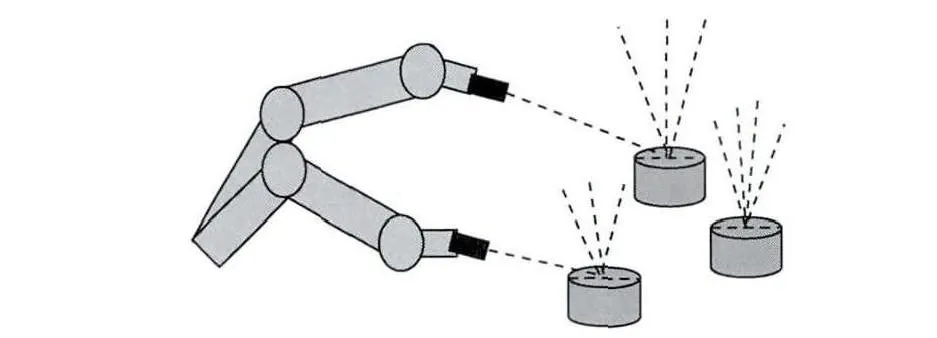
图2 多点约束标定原理

实验中用到的PSD是高精度的位置传感器，可以实现高精度定位，可以认为PSD在每一个位置上的多条激光线准确交于同一个点，即PSD的中心点。由于机器人系统中存在零位误差，通过运动学正解求出末端姿态，进而得到每个位置上的多条激光线在机器人坐标系下的直线方程，这些直线方程存在误差，从而多条直线方程两两之间求得的交点并不是同一个点。因此，单点约束的标定过程就是通过迭代计算使得标定后两两之间的交点收敛为同一点，即PSD中心点，而多点约束就是在每一位置上的交点分别收敛至各位置上PSD的中心点。

3．2 激光线模型

在标定系统中激光器在末端执行器上的位置是固定的，则激光线在机器人末端坐标系下的直线表示为：

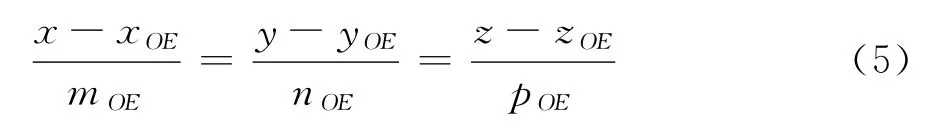
其中，（xOE，yOE，zOE）是激光线通过的某一固定点在机器人末端坐标系下的坐标；（mOE，nOE，pOE）是该激光线在机器人末端坐标系下的单位方向向量；激光线在机器人坐标系下的直线方程为：

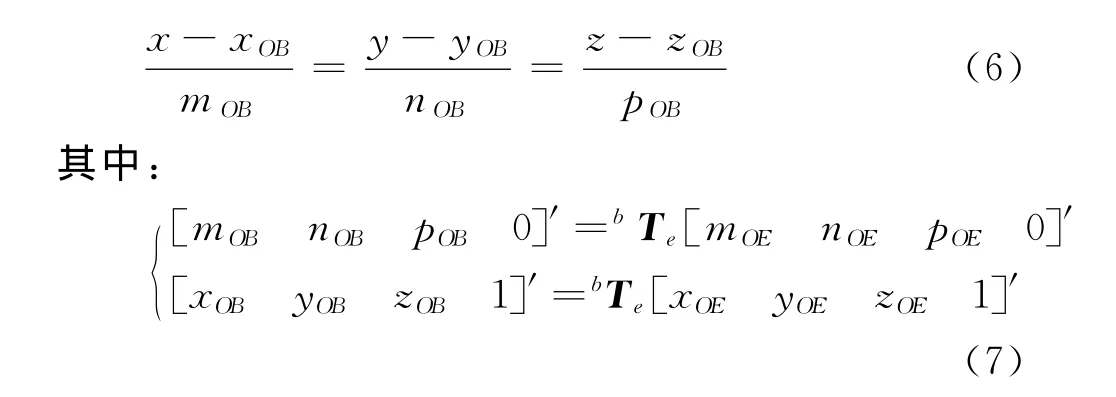
任意一条激光线方程记为L（mi，ni，pi，xi，yi，zi），从而可以求出任意两条激光线的交点或者两条激光线之间公垂线的中点。

3．3 优化模型

单点约束模型中，机器人末端限制最终激光束交于PSD的中心点，求出每2条激光线之间的交点，当交点不存在时用这2条激光线公垂线的中心点代替交点，以每一交点到所有交点平均值之间的距离作为优化目标函数：

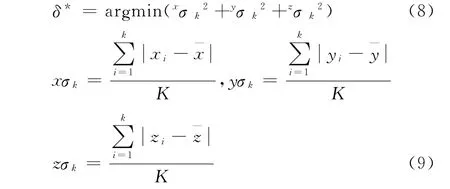
多点约束中将PSD放置在机器人可达空间的多个位置，在每一个位置上进行较少次数的激光定位，以每一个位置上的交点到其交点平均值之间的距离作为优化目标函数：

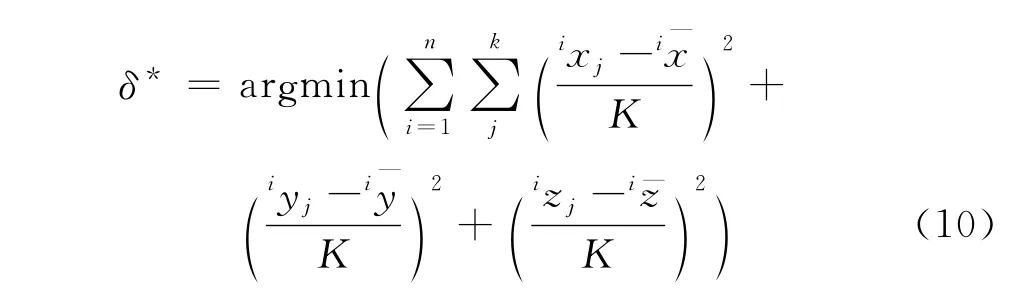
其中，n表示PSD放置的位置个数；为每一位置上，激光定位的次数。

本文用LM［11］算法对零位角进行迭代补偿，使得单点约束和多点约束下的交点均能收敛，标定出机器人的零位误差。

4 标定系统

4．1 标定装置

本文中标定系统的结构如图3所示，主要包括工业机器人ABB IRB120，固定在末端执行器上的激光器，采集卡以及PSD（位置敏感器件）。

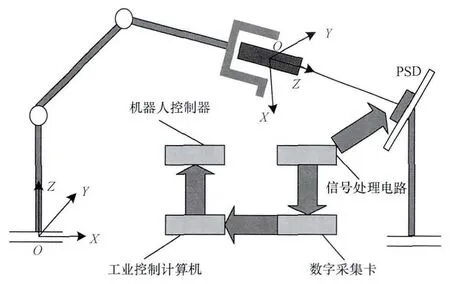
图3 标定系统结构

4．2 标定步骤

标定步骤如下：

（1）将PSD装置放在工业机器人有效工作空间内，控制机器人，使得激光束近似垂直投射到PSD表面，并精确定位到PSD的表面中心点，记录该位置的关节角［12］。

（2）在此位置的基础上，调整机器人的位姿进行相同的M－1次定位，则PSD在该处共进行了M次定位，M条激光线投射到相同的点，即PSD在当前位置下的中心点，实现了单点约束数据采集。

（3）移动PSD，重复步骤（1）和步骤（2），在该位置进行K（K＜M）次定位。

（4）移动PSD至其他N－1个位置，重复步骤（3），实现N个位位置上较少次数的激光定位，记录N×K组关节角，完成多点约束的数据采集。

（5）根据优化模型，分别计算单点约束和多点约束的标定结果。

5 仿真实验与结果分析

本文主要研究点约束中约束点的分布对零位标定结果的影响，分别进行单点约束与多点约束下的仿真与实验。实验平台是ABB IRB120工业机器人，图4为实验系统图。

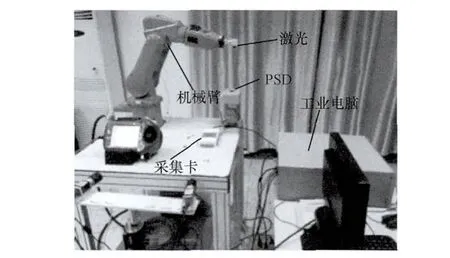
图4 实验系统

仿真1在仿真的机器人系统中，只含有零位误差，不含其他系统噪声，设定同样的零位误差值，分别对单点约束以及多点约束进行仿真。

单点约束仿真数据为7组点，即将PSD在某一位置上进行7组定位，仿真结果如图5所示。

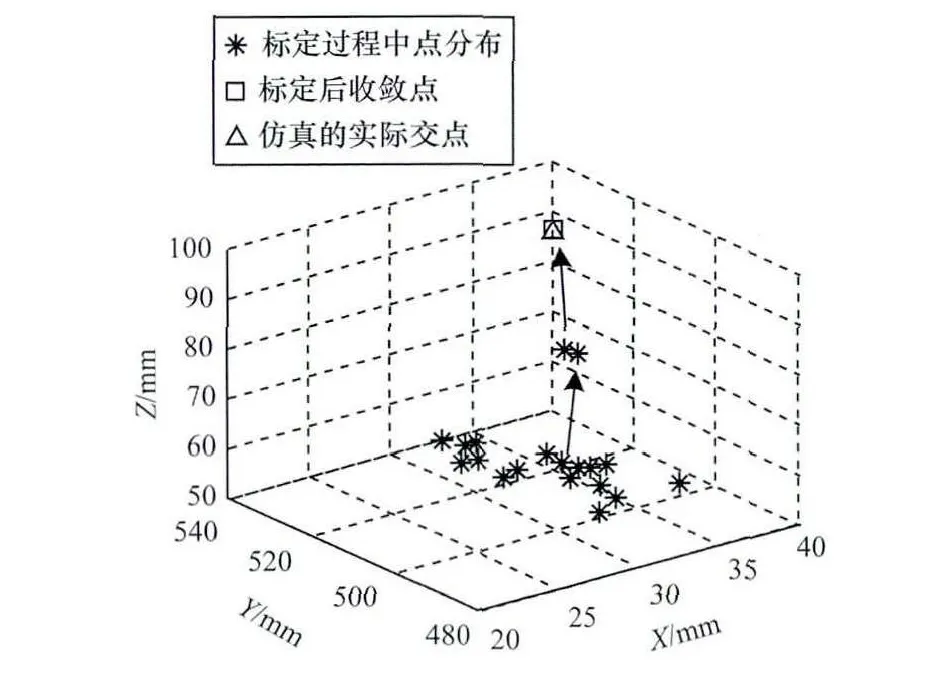
图5 单点约束仿真结果

在多点约束仿真中，将PSD放置于3个位置，在每一个位置上进行4次激光定位，仿真结果如图6所示。

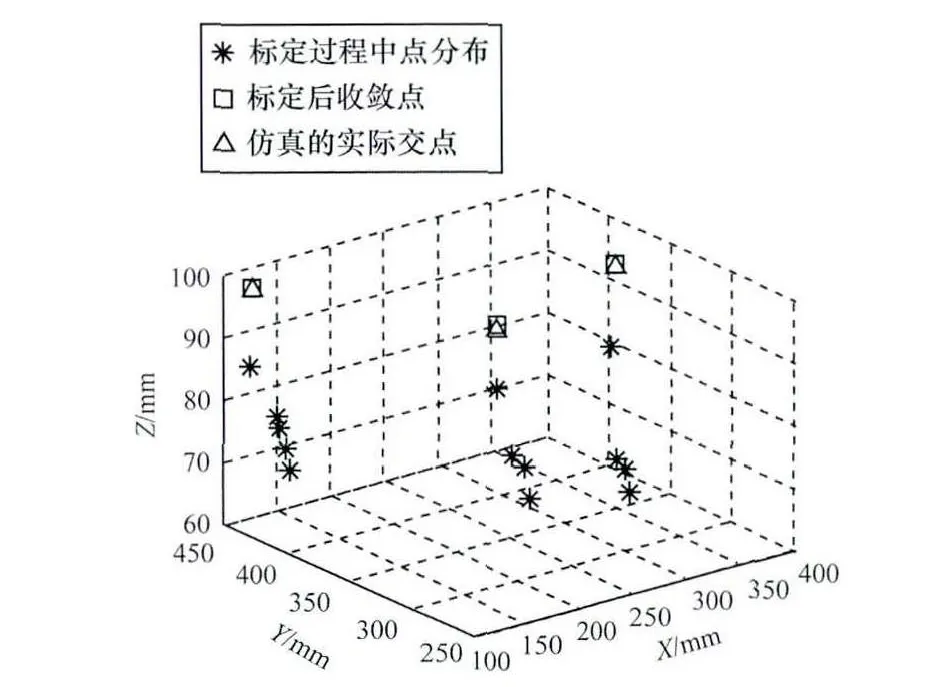
图6 多点约束仿真结果

仿真2向仿真机器人系统中添加噪声，本文的仿真过程中向机器人DH模型中第4个关节的杆件长度a以及关节平移量d加上随机误差。针对相同的零位误差，多次改变系统的随机误差，保证单点约束和多点约束具有相同的误差源。系统噪声如下：

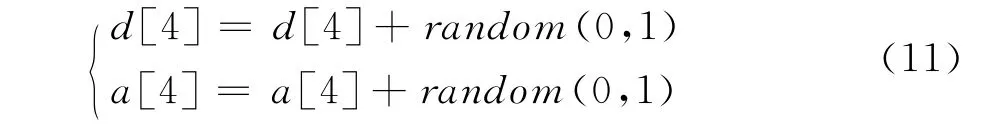
仿真中，给d和a随机加上一个（0，1）之间的值，进行多次系统误差的添加，单点约束和多点约束的标定结果如表1所示，其实际值为－2．000。当给定不同系统误差时，针对相同的零位误差，多点约束的结果更加接近实际误差值，即多点约束在存在系统误差情况下，标定结果与实际值之间的平均误差比单点约束低。

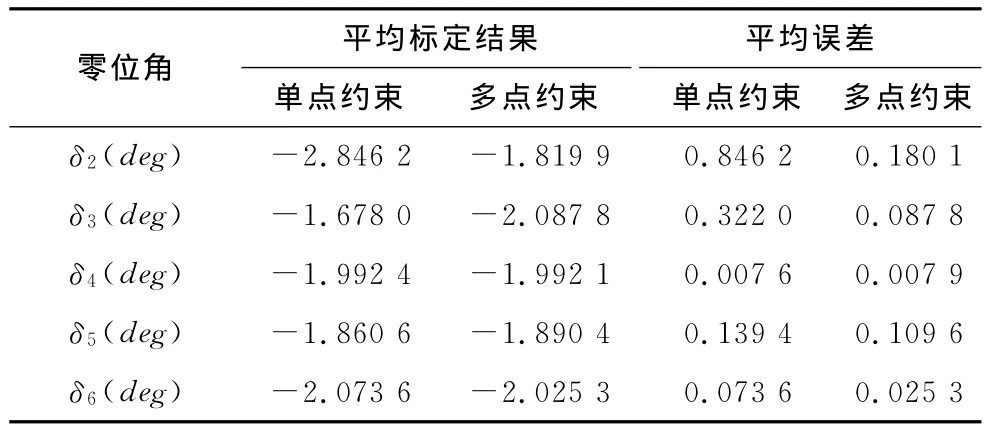
表1 单点约束与多点约束标定结果对比

实验基于ABB IRB120工业机器人，分别对单点约束以及多点约束进行标定实验，单点约束中将PSD放置在机器人工作空间的任一位置进行6次定位。多点约束将PSD分别放置于机器人工作空间中相隔比较大的3个位置，每个位置上进行3次定位。实验结果如表2所示。

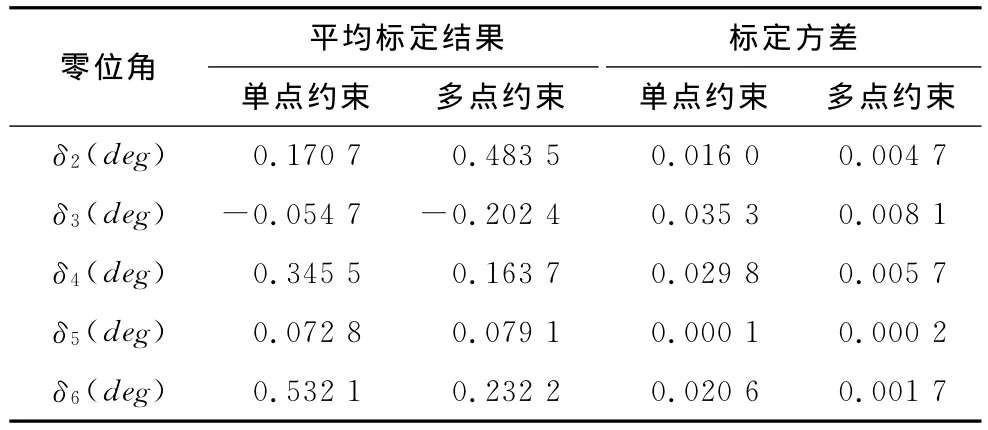
表2 IRB120单点约束与多点约束对比

因为机器人存在系统误差，以及定位过程中存在的误差，所以单点约束和多点约束的标定结果有一定偏差。多次实验中，多点约束的标定结果比单点约束更稳定。

6 结束语

本文主要研究点约束进行零位标定时，约束点空间分布对标定结果的影响，分别进行了单点约束和多点约束在无系统误差和有系统误差下的零位标定的仿真，并基于ABB IRB120对机器人零位进行标定。仿真结果表明，在无系统误差的情况下，单点约束和多点约束均能快速准确地标定机器人的零位误差，在存在其他系统误差的情况下，多点约束有更好的标定结果。下一步将研究不同的系统误差对零位标定结果产生的影响是否存在联系。

［1］龚星如，沈建新，田 威．工业机器人的绝对定位误差模型及其补偿算法［J］．南京航空航天大学学报，2012，44（1）：60－64．

［2］刘振宇，陈英林，曲道奎，等．工业机器人标定技术研究［J］．机器人，2002，5（1）：447－450．

［3］王东署，迟健男．机器人运动学标定综述［J］．计算机应用研究，2007，24（9）：8－11．

［4］任永杰，邾继贵，杨学友．利用激光跟踪仪对机器人进行标定 的 方 法 ［J］．机 械 工 程 学 报，2007，43（9）：195－200．

［5］李定坤，叶声华，任永杰．机器人定位精度标定技术研究［J］．计量学报，2007，28（3）：195－200．

［6］叶声华，王 一，任永杰．基于激光跟踪仪对机器人运动学参数标定方法标定的方法［J］．天津大学学报，2007，40（2）：195－200．

［7］Chen Heping，Fuhlbrigge T，Choi S．Practical Industrial Robot Zero Offset Calibration ［C］／／Proceedings of IEEE Conference on Automation Science and Engineer－ing．Washington D．C．，USA：IEEE Press，2008：516－521．

［8］张建忠．机器人连杆参数的视觉标定［J］．制造业自动化，2004，26（11）：32－34．

［9］Liu Yong，Xi Ning，Chen Heping，et al．An Automated Method to Calibrate Industrial Robot Joint Offset Using Virtual Line－based Single－point Constraint Approach［C］／／Proceedings of IEEE Conference on Intelligent Robots and Systems．Washington D．C．，USA：IEEE Press，2009：715－720．

［10］Liu Yong，Xi Ning，Zhao Jianguo，et al．Development and Sensitivity Analysis of a Portable Calibration System for Joint Offset of Industrial Robot［C］／／Proceedings of IEEE Conference on Intelligent Robots and Systems．Washington D．C．，USA：IEEE Press，2009：3838－3843．

［11］Levenberg K．A Method for the Solution of Certain Non－linear Problems in Least Squares ［J］．The Quarterly of Applied Mathematics，1944，2（1）：164－168．

［12］Liu Yong，Xi Ning，Yan Shentao，et al．High－accuracy Visual／PSD Hybrid Servoing of Robotic Manipulator［C］／／Proceedings of International Conference on Advanced Intelligent Mechatronics．Washington D．C．，USA：IEEE Press，2008：217－222．