基于层次结构的三维矢量场建模

陈国栋，曾惠燕

（福州大学物理与信息工程学院，福州350108）

1 概述

近年来，随着矢量场应用的逐渐广泛，矢量场在工程分析和科学计算中扮演着越来越重要的角色，如何构建可用性强的矢量场开始成为当前计算机视觉、计算机图形学和图像处理领域的研究热点。一般来说，在三维空间中指定三维取向比在二维空间中指定二维取向困难，因此，在三维空间中构建矢量场比在二维平面或三维表面困难，这就使得设计一个合适的用户界面对三维矢量场的建模至关重要。本文以自然界中许多物体纹理都是基于三维矢量的纹理拼接为理论依据，构建一系列三维矢量，其中，每个三维矢量都是由3个两两正交的矢量组成。

2 相关工作

早期研究者们在矢量场建模过程中所采用的技术都较为简单，如使用高斯径向基函数进行插值、对网格顶点颜色使用低通滤波以及人工绘制矢量场，对矢量场的研究仍存在很多不足。为改善早期的方法，研究者陆续提出了许多种构建矢量场的方法，如Zhang等人［1］提出生成对称张量场的方法，Liu等人［2］提出一种生成共轭矢量场的方法。这些方法的典型优点包括增加场拓扑结构的控制能力，以及运用简单的公式进行插值操作，被广泛用于程序城市设计、建筑玻璃结构的四边形网格设计等。然而，上述技术针对的都是在二维平面或三维流行曲面的矢量场，而不是三维空间中的矢量场。

自从Owada［3］设计了一个用于浏览物体内部纹理的交互系统之后，对三维矢量场的建模才逐渐受到研究者们的关注，用户仅需在三维模型的横截面放置若干个箭头，同时，采用径向基函数进行插值便可以生成三维矢量场，然后利用三维模型横截面上的矢量场引导二维纹理走向。文献［4］提出一种基于草绘的发型建模系统，利用拉普拉斯算法插值生成具有曲线特征的三维矢量场引导头发生长，用户可根据自己的喜好设计不同的发型。文献［5］提出根据用户在三维空间上定义的3个相互正交的矢量场合成各向异性体纹理的方法，通过在三维表面或在任意的三维平面绘制曲线，将曲线点上的切线作为约束条件生成矢量场。然而，目前三维空间矢量场建模的重点仅在于矢量场的表示和插值的研究，设计的界面缺乏友好性，且不适合引导具有层次结构的物体。

科学计算可视化是指运用计算机图形学、图像处理技术和辅助设计的方法，将抽象、复杂的数据转换成人们容易理解的、具有特定含义的图形与图像在屏幕上显示出来并进行交叉处理的理论、方法和技术［6－7］。矢量场可视化是科学计算可视化中最具挑战性的课题之一，它以直观的图形图像显示场的运动［8－9］。传统的矢量场可视化方法包括图标法、线图标法、箭图标和面图标法等，主要是通过绘制几何图标来显示矢量场，其重点在于描述部分特征点的矢量信息，缺乏对矢量场的整体把控能力，因此，已经无法满足用户的需要。基于纹理的矢量场可视化方法利用纹理表达了矢量场的方向变化等细节信息，由于粒子的集合构成了纹理，带有色彩信息的粒子的运动轨迹即可表示矢量场。该方法有点噪声和线积分卷积（Line Integral Convolution，LIC）方法［10］。

以上述研究为基础，本文设计并实现一种基于层次结构的三维矢量场建模方法，以血管作为三维模型，沿用户定义的三维矢量场粘贴纹理样本块，合成血管体纹理。

3 血管模型的构建

利用开源的三维网格生成库TetGen，将血管表面网格模型转化为以四面体为单元的网格模型，生成ele文件和node文件。ele文件保存了模型的四面体总数和各四面体顶点的索引值，node文件则保存了各四面体顶点的位置信息。本文构建的血管体模型共有2 117个四面体，556个顶点。ele文件如图1所示。以血管的四面体网格作为输入，输出由用户自定义的矢量场所引导的血管纹理。

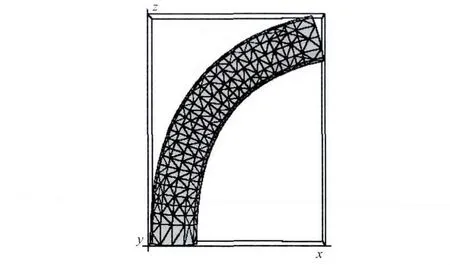
图1 血管的ele文件

3．1 深度场梯度方向定义

血管作为多层次结构，由里向外包含血液、血管内膜、血管中膜和血管外膜。因此，可借鉴基于纹理的矢量场可视化方法，用户首先在血管模型中辅以颜色属性生成深度场，依次选择蓝色、蓝绿色、绿色、黄色和红色作为模型从里到外的颜色，并为各颜色分配深度值，分别为0，0．25，0．5，0．75和1；其次，利用粉刷工具将模型的外表面涂抹为红色；再次，对模型进行适当切割，用蓝色画笔模拟血管的轴线。最后，为准确计算深度场的梯度方向（y方向上的分量），考虑将深度值作为约束条件，利用薄板样条函数插值三维欧几里得空间获得光滑变化的深度场。同时，运用移动立方体算法［11］提取等值面。深度场生成示意图如图2所示。

图2 深度场生成示意图

3．2 第2个方向场的构建

用户在各等值面上，利用箭图标定义纹理的走向，即x方向上的分量，第3个方向场则是前2个矢量的矢量积。因箭图标均位于各等值面上，这就保证了第2个方向场始终与深度场的梯度方向保持垂直。

4 拉普拉斯平滑

由于用户自定义的矢量场，只有部分采样点具有方向定义，模型上大多数采样点仍缺乏方向信息，因此需要利用插值技术构建整个模型的矢量场。因为拉普拉斯平滑算法相比其他空间插值技术的基本优势是将域拓扑考虑到插值过程中，且在尽可能满足用户定义的约束条件下最小化分配给网格顶点的值之间的差异，所以本文利用拉普拉斯平滑算法分别插值3个不同方向的矢量场。

双溪村：土壤中全钾为丰富水平，铜、钙、锰、硒为中等水平，镁、钼、全氮、全磷、硫为缺乏水平，显示了营养元素严重失衡，且养分元素含量均较低。

假设xi为分配给顶点vi（i＝1，2，…，n）的x分量，拉普拉斯算子定义为：

其中，Ni是顶点vi的相邻点集；wij代表相应的权重。

为使相同层次的插值结果比不同层次的插值结果平滑，设置权重为：

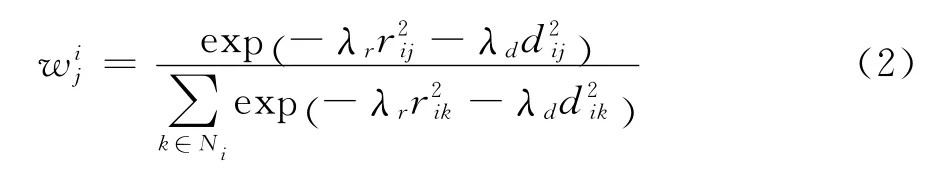
其中，rij表示顶点vi和vj间的欧几里得距离；dij是vi和vj的深度值之差；λr和λd都为常量，控制在深度方向上的平滑度（分别将它们设置为1和5）。目标是在用户定义的约束条件下最小化拉普拉斯算子。

将用户绘制的箭头线作为给定的方向约束，每条方向线都由一系列的小片段构成，把每一小片段作为定义三维空间中离散点的归一化约束矢量。假设约束矢量c位于三维空间中的位置点p，查找出最靠近于点p的四面体T，以加权和的形式作为约束条件：

其中，i1，i2，…，i4代表四面体T4个顶点的索引；cx是矢量c的x方向上的分量。权重因子w1，w2，…，w4表示如下：

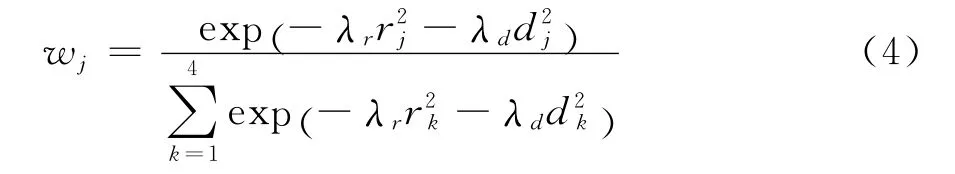
其中，rj为点p到顶点vij的欧几里得距离；dj为点p和顶点vij的深度差。

给定约束条件的能量函数表示为：

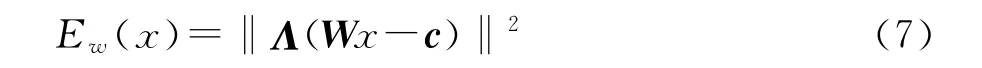
其中，W 为权重矩阵；c＝（cx1，cx2，…，cxm）T；对角矩阵Λ＝diag（λ1，λ2，…，λm）调节各顶点上的权重。为达到在满足约束条件下，生成满足用户的光滑矢量场，需求出能量和最小时x的取值，即：

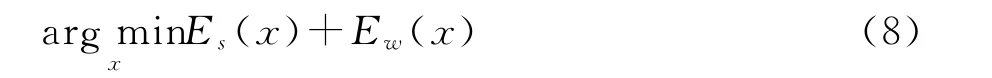
利用最小二乘法可求出x解：

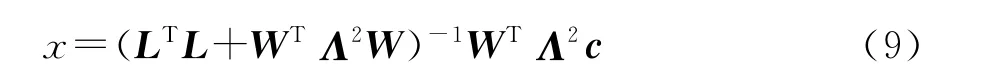
在通常情况下，矩阵L和矩阵c都为稀疏矩阵，方便利用现存的稀疏矩阵求解器进行求解。

拉普拉斯平滑算法并不能保证所得到的第2个方向上的矢量场总是垂直于深度场的梯度方向，因此，该系统自动删除平行于深度场梯度方向的矢量。第2个方向上的插值结果可采用基于四面体网格数据的流线追踪算法［12］以彩色箭标及流线的形式对其进行可视化操作，如图3所示。

图3 可视化结果

5 体素的计算

5．1 边界体素计算

本文采用光纤投射算法［13］计算边界体素，分别沿平行于空间坐标轴的3组平行线发射光线，由负方向向正方向进行扫描，计算与模型表面交叉时的位置信息，然后将最靠近此位置的网格点作为边界体素。边界体素基本几何信息主要由实体表面的三角面片表示：

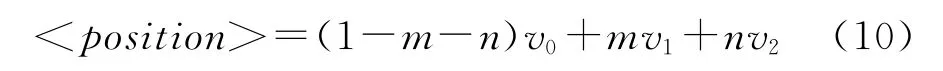
其中，i代表三角面片Pi的索引值；m，n为参数；v0，v1，v2为三角面上的3个顶点。利用边界体素所蕴含的模型上点的位置信息，计算切割横截面的边界。

为计算模型表面与切割曲线相交的边界体素，将模型表面的面片全部投影到与切割曲线所在的平面上，判断投影的三角面片与切割曲线是否存在交线。设lili＋1为切割曲线上的一条线段，Patch为模型表面的面片数组，数组中的面片全部标记为“unvisited”，步骤如下：

（1）从Patch中逐一取出三角面片ΔABCi，投影后得到Δabci。

（2）对Δabci与切割曲线段lili＋1进行求交运算，同时，将 ΔABCi标记改为“visited”，若相交，则将ΔABCi相邻的3个三角面片放入队列，否则取下一个面片。

（3）从队列中取出标记为“unvisited”的三角面片，判断此面片与线段lili＋1是否相交，同时，将此面片标记为“visited”，若相交则将其相邻的三角面片放入队列，重复此步骤，直到队列为空。

5．2 四面体的体素化

由于上述获得的矢量场只被定义在四面体的网格顶点，将四面体转换为体素计算三维矢量场。同样采用光线投射算法［13］，对网格中的每个四面体，分别沿x，y，z方向进行扫描，以获得一组属于该四面体的体素。然后线性插值四面体4个顶点的深度值，将插值结果分配给对应四面体的体素。最后，将四面体4个顶点矢量的权重和作为对应四面体体素的矢量。

6 实验结果与分析

本文利用Visual C＋＋和OpenGL在PC机上实现了上述算法，PC机的配置为Intel（R）Core（TM）i5－3317U1．7GHz的 CPU，8GB的 RAM，Intel GMA HD 4000核心显卡。将血管三维纹理样本块沿上述算法生成的三维矢量矢量场进行粘贴，所合成的血管纹理效果图4所示。

图4 纹理合成图

7 结束语

本文以具有层次结构特征的肝动脉为研究对象，利用颜色属性和箭图标定义物体上的点在三维空间中的矢量约束，运用拉普拉斯算法插值出整个模型的矢量场。实验结果表明，本文设计的三维矢量场能成功地引导物体纹理进行合成。另外，该方法所设计的界面不仅直观友好，且实用性强，能用于引导纤维生长等多种场合。同时，深度场的设计不仅非常适合处理具有层次结构的三维模型，而且方便用户通过变换深度层次直观地了解内部矢量场的变化情况。目前，该方法存在的主要缺点在于用鼠标模拟物体纹理走向时缺乏精确性，可以在后期的研究中进行拓展，即将纹理图像映射到模型的各层次面上，跟踪实际的纹理走向。

［1］Zhang E，Hays J，Turk G．Interactive Tensor Field Design and Visualization on Surfaces［J］．IEEE Transactions on Visualization and Computer Graphics，2007，13（1）：94－107．

［2］Liu Yang，Xu Weiwei，Wang Jun，et al．General Planar Quadrilateral Mesh Design Using Conjugate Direction Field［J］．ACM Transactions on Graphics，2011，30（6）：61－64．

［3］Owada S，Nielsen F，Okabe M，et al．Volumetric Illustration：Designing 3DModels with Internal Textures［J］．ACM Transactions on Graphics，2004，23（3）：322－328．

［4］Fu Hongbo，Wei Yichen，Tai C L，et al．Sketching Hairstyles［C］／／Proceedings of the 4th Eurographics Workshop on Sketch－based Interfaces and Modeling．New York，USA：ACM Press，2007：31－36．

［5］Zhang Guoxin，Du Songpei，Lai Yukun，et al．Sketch Guided Solid Texturing［J］．Graphical Models，2011，73（4）：59－73．

［6］李海杰．基于OpenGL的矢量场可视化方法研究与应用［D］．沈阳：东北大学，2013．

［7］Ryabinin K，Chuprina S．Adaptive Scientific Visualization System for Desktop Computers and Mobile Devices［J］．Procedia Computer Science，2013，18（1）：722－731．

［8］顾耀林，吉晓娟．基于时间延迟的矢量场可视化方法的应用研究［J］．计算机工程，2007，33（2）：186－188．

［9］苏 芳．基于GPU的二维矢量场可视化点噪声方法的研究与实现［D］．青岛：中国海洋大学，2011．

［10］Karch G K，Sadlo F，Weiskopf D，et al．Visualization of 2DUnsteady Flow Using Streamline－based Concepts in Space－time［J］．Journal of Visualization，2015，18（4）：1－14．

［11］王媛媛．基于自适应细分方法的医学图像三维重建及可视化技术研究［D］．杭州：浙江大学，2010．

［12］王成恩，姜传彦，武新宇．基于几何图形的矢量场可视化技术［J］．东北大学学报：自然科学版，2011，32（3）：327－330．

［13］江兆尧，路 游，贾广忠，等．基于OpenGL的光线投射算法的研究［J］．计算机技术与发展，2010，20（3）：218－220．