单片机在倒立摆控制系统的应用❋
2014-12-31亢健
亢 健
(太原科技大学 电子信息工程学院,山西 太原 030024)
0 引言
倒立摆作为一种典型的控制系统实验装置,具有非线性、自然不稳定等特性,常用来作为检验某种控制理论或方法是否合理的典型方案。一阶倒立摆系统能用多种理论和方法来实现其稳定控制,如PID、自适应、状态反馈、模糊控制及人工神经元网络等多种理论和方法都能在倒立摆系统控制上得到实现[1,2]。
1 系统构成及工作原理
图1为一阶旋转倒立摆结构示意图。直流电机作为唯一的动力装置,与旋臂保持刚性连接,带动旋臂在水平面内旋转,旋臂的一端通过转轴(本系统选用电位器角度传感器)与摆杆连接,摆杆可做垂直于旋臂的圆周运动。在自然状态下,摆杆为竖直下垂状态。倒立摆控制的目的是通过控制直流电动机的运动状态,使摆杆保持倒立状态。
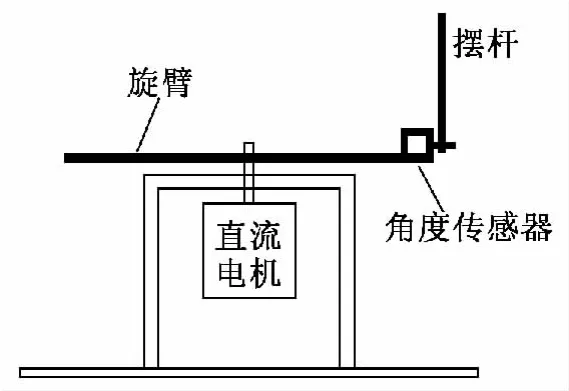
图1 倒立摆结构示意图
系统工作原理如下:摆杆摆动时,角度传感器检测摆杆的角度,根据角度传感器的输出特性,其输出电压经A/D转换器转换成电压数字量,该数字量与期望的值进行比较产生偏差,通过单片机对该偏差进行处理,即PID控制运算,根据运算结果产生控制信号控制电机和旋臂的转动,使摆杆的角度与期望的角度更接近。
倒立摆控制系统结构框图如图2所示,单片机(51单片机)为控制器,直流电机为执行器,倒立摆为被控对象,倒立摆角度为被控量,角度传感器和模数转换器构成反馈回路。
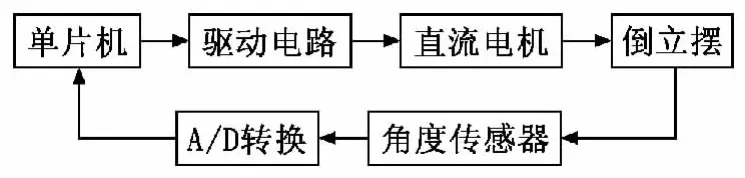
图2 倒立摆控制系统结构框图
2 倒立摆控制系统的硬件设计
2.1 单片机最小系统
该系统中选用了STC90C51单片机,该型单片机具有以下特点:①八位MCU核,与传统8051兼容;②大容量存储空间,包括64kB程序空间,1 280B SRAM等;③具有4个八位并行I/O口,3个定时/计数器,2个外部中断源和1个全双工UART传输口;④5V供电时,最高支持80MHz振荡频率,具备高速浮点运算能力,适合倒立摆系统等较为复杂的控制系统使用。51单片机最小系统如图3所示[3]。
2.2 摆杆角度检测
检测摆杆角度所用到的角度传感器种类非常多,常用的有电位器式角度传感器、光电编码器、陀螺仪模块等。由于电位器式角度传感器原理简单,检测精度取决于所用A/D转换器的精度,成本相对较低,因此,综合多方面要求,本系统选用电位器式角度传感器。
传感器返回的电压信号无法被单片机直接识别,所以需要通过A/D转换,将模拟电压信号转换为二进制数的形式,然后单片机才能计算出偏差,进而产生相应的输出。A/D转换器常用的有8位和12位输出,在本系统中选用8位A/D转换器即可满足控制要求,其型号选用ADC0809,相应电路原理图见图4。
A/D转换器的时钟脉冲为单片机ALE引脚输出的脉冲经74LS74芯片分频之后得到,A/D转换器的8位数字信号通过单片机的P0口进行采集与处理。
2.3 驱动电路
本系统选用的直流电机额定电压为24V,额定功率为30W,单片机的I/O口不足以提供如此大的驱动能力,故需采用驱动电路。常用的直流电机驱动芯片为L298N,可驱动两路直流电机,最大驱动电压为46 V,最大电流2A~3A,满足设计要求。直流电机驱动电路如图5所示。
图5中,L298N的ENA为使能端,可作为单片机PWM(脉宽调制)控制端,控制直流电机转速;IN1和IN2为信号输入端,OUT1和OUT2为输出端,输出状态与输入状态对应,控制直流电机转向。输出端的二极管为续流二极管,起保护电动机线圈的作用。

图3 51单片机最小系统

图4 A/D转换电路

图5 直流电机驱动电路
3 倒立摆控制系统的软件设计
3.1 控制算法
本系统采用PID控制算法,PID算法适用于负荷变化大、容量滞后较大、控制品质要求高的控制系统。PID算法有3个可设定参数,即比例放大系数KP、积分时间常数TI、微分时间常数TD。比例调节的作用是使调节过程趋于稳定,但会产生稳态误差;积分作用可消除被调量的稳态误差,但由于积分饱和等原因可能会使系统振荡甚至使系统不稳定;微分作用能有效地减小动态偏差[4]。其传递函数为:
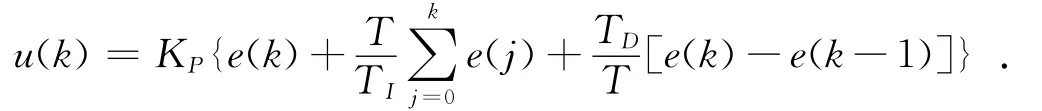
其中:u(k)为第k个采样时刻的输出;e(k)为第k个采样时刻的偏差值;T为采样周期;KP为比例放大系数;TI为积分时间常数;TD为微分时间常数。
在实时性要求较高的倒立摆系统中,积分作用常常使系统对偏差的调节变慢,使动态相应变慢。因此要尽量弱化或者消除积分作用,使用PD调节规律即可。在该系统中,输入变量为给定值与实际检测到角度的差值,输出变量控制所产生的PWM波形的占空比。由于旋臂、摆杆以及电动机的各项参数很难准确把握,且干扰较多,难以建立精确的数学模型,因此采用试验法整定参数的数值,即根据系统表现出的状态,调节各参数的数值,直至系统达到稳定。
3.2 程序流程图
倒立摆系统主程序流程图见图6。其中,U为PID运算的输出值,为输出PWM波形的占空比,由于所选单片机不具备专用PWM输出引脚,需要利用定时器T0模拟其波形输出,定时器T0中断子程序流程图见图7。在本系统中,采样周期选择为10ms,由定时器T1控制,定时器T1中断子程序流程图见图8。
4 系统测试
本系统测试所用到的倒立摆模型为自制简易模型,测试过程如下:外力将摆杆拉起至接近倒立状态(与倒立状态相差20°左右);给系统上电,同时撤去外力,观察到摆杆迅速呈倒立状态,经过几次调整,即可长时间保持倒立状态。系统达到稳定状态的效果如图 9所示。

图6 主程序流程图
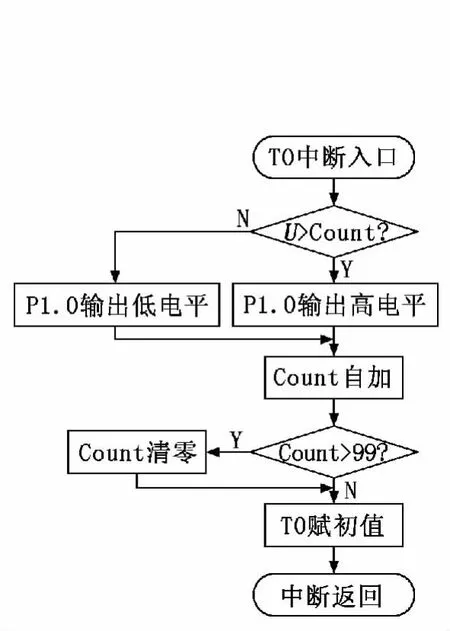
图7 定时器T0中断程序流程图

图8 定时器T1中断程序流程图

图9 系统稳定状态
在摆杆保持倒立状态时,施加一扰动,即轻碰摆杆或旋臂,系统经过短时间的调整之后,仍可以自动调节至稳定状态,说明该系统具备较强的鲁棒性。
5 结论
本系统采用单片机作为一阶旋转倒立摆系统的控制器,执行了数据采集、数据处理(PID运算)、控制直流电机运行状态等操作,成功使该系统稳定,其经济性和实用性得到了很好的展现。同时也体现了经典PID控制理论在一阶倒立摆系统中使用时良好的控制效果。
[1] 张飞舟.利用单片机实现智能控制[J].电子技术应用,1998(9):27-29.
[2] 江晨.旋转式倒立摆的控制算法研究及试验系统设计[D].苏州:苏州大学,2010:1-2.
[3] 张毅刚,彭喜源.MCS-51单片机应用设计[M].哈尔滨:哈尔滨工业大学出版社,2007.
[4] 王建华.计算机控制技术[M].北京:高等教育出版社,2009.
