去除阴影后利用霍夫直线变换检测茶叶中的杂质
2014-12-31陈培俊伍铁军
陈培俊,伍铁军
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
图像中的阴影直接影响了目标的检测,并对图像匹配的精度、模式识别的准确度以及目标提取的自动化程度造成损害,导致目标连接及目标外形轮廓严重扭曲变形等多种问题。因此,去除阴影对于提高目标检测的精度具有十分重要的意义。直线检测是模式识别和图像分析中的一个重要内容,它可以使图像的表示更简洁,可以很好地完成图像识别任务。而霍夫变换(Hough Transform)是直线检测的一个典型且可靠的方法。霍夫变换的主要优点是能够不受图像中噪声的影响,并且可以处理局部遮挡和覆盖的情况。但是由于它是一种穷尽式搜索,进而导致算法有很高的空间复杂度和计算复杂度。各国研究人员多年来进行了大量研究[1],提出了各种改进算法来提高霍夫变换的速度。本文利用霍夫变换检测图像中具有直线特征边缘的杂质,并结合两点表决的方法来改进霍夫变换。
1 去除阴影
根据阴影的光学属性可知,可以将阴影区看作是半透明区域。有研究表明,对于阴影区域内的像素,其灰度值是相应背景像素灰度值的k倍[2],且在这个阴影区域内k值的波动很小,实验发现这个比例范围为0.4~1[3]。目标区域的灰度值相对于背景区域变化范围较大,而梯度算子能够突出灰度变化较大的区域,因此对图像采用多梯度算子[4],能够检测出阴影区域。
阴影区域的灰度值变化一般比较均匀,而阴影与目标的边界处会出现大的灰度变化,可采用多梯度算子寻找边界,本文定义了垂直、水平和对角方向上的3对梯度算子,如图1所示。

图1 不同方向的梯度算子
然后采用式(1)组合算子的方式得出梯度图:

其中:G1,G2分别为不同算子得出的梯度图;g为组合算子后得到的梯度图。
利用不同的梯度算子可以计算不同方向的变化幅度,进而检测出该方向的边界。Gx1和Gx2适用于检测垂直方向的边界,如图2(a)所示;Gy1和Gy2能够检测出水平方向的边界,如图2(b)所示;Gd1和Gd2可以分别检测两种对角方向的边界,如图2(e)和图2(f)所示;而利用Gx1和Gy1的组合算子可以检测出图2(c)所示的边界;Gx2和Gy2的组合算子适用于检测图2(d)所示的边界。

图2 不同梯度算子检测的边缘示意图
根据式(1)计算图1的3对梯度图并记为gn,n=1,2,3。给定一个阈值Tg,如果梯度图中的像素灰度值小于Tg则被认定为阴影,对6个方向上小于阈值的像素做或运算,最终得到二值图像,记为G(i,j):
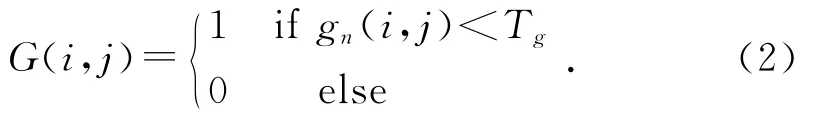
这样就能得到去除阴影的二值图像。多梯度算子判断的阴影区域中的像素灰度值是连续的,利用多梯度算子对阈值分割的二值图像进行或运算可以达到去除阴影的目的。
2 Hough直线变换
2.1 标准Hough变换原理
Hough直线变换是从二维空间到极坐标空间的一种映射,这种映射表现为二维空间上的一点(x,y)到极坐标空间上的某条曲线的对应关系,映射关系表达式为:

其中:ρ为直线到原点的距离;θ为直线的法线与x轴的夹角。
霍夫变换的原理图如图3所示,图3(a)显示图像平面的一个点(x0,y0),图3(b)显示图3(a)中参数ρ和θ不同时的许多线,这些线隐含在(ρ,θ)平面内的点,放在一起就形成了一条特征曲线,如图3(c)所示。根据Hough变换的原理,其算法描述为:
(1)在参数(ρ,θ)空间中建立一个累加数组Q(m,n),并将每个元素初始化为零(m,n分别为ρ和θ的等份数)。
(2)将图像中的点(x,y)代入式(3),遍历θ参数的每个值,计算出相应的ρ值。
(3)根据ρ和θ的值对数组Q(m,n)进行累加。
(4)对图像中的点都做完处理后,计算数组中的最大值,得出相应的参数ρ和θ,在图像中即映射为一条直线。

图3 霍夫直线变换原理图
霍夫变换算法虽然受噪声影响较小,鲁棒性较强,但其计算量大,在极端情况下,其运算复杂度为O(n3)。使用霍夫变换来检测直线的图像一般为二值图像,假设二值图像中有m个特征点,将θ离散化为Nθ个空间(若θ变换范围为π,变换步长为s,那么Nθ=π/s),则该幅图像的霍夫变换次数为mNθ,其乘法运算次数为2mNθ,因此要加快霍夫变换的运算速度可以从以下几个角度[5]考虑:①减少参与运算点的个数m;②减少极角θ的变化范围;③增大角度的分辨率s。由于增大角度分辨率会影响直线检测的精度,因此,在保证精度的情况下只能从减少参与运算点的个数和角度变换范围方面来提高霍夫变换的速度。
2.2 霍夫变换的改进
根据霍夫变换原理可知图像中的一个点对应参数空间中的一条曲线,反之参数空间中的一个点对应着图像中的一条直线。正是因为这种映射,导致进行霍夫变换时必须计算图像点对应参数空间中曲线所有可考虑参数的所得函数值,这样的计算工作是很繁重的。
而图像中两点能确定一条直线,一条直线对应参数空间的一个点,通过这种对应关系就不需要在参数空间中对所有参数都进行计算。我们将这种两个图像点确定参数空间中的一点的算法称为两点组合表决算法[6],但是直接使用这种方法并不能有效地减少计算量,可以将图像分成多个小的图像块或子图,其计算量会大大减少,具体算法如下:
(1)把原始图像分割成NS个子图像块。
(2)从图像块中任取两个特征点(xi,yi)和(xj,yj)进行两点表决变换,根据式(4)计算经过这两个点直线的参数ρ和θ,并对参数空间的累加数组Q(ρ,θ)进行累加,根据数组的最大值得到每一个图像块中的直线参数ρ和θ。
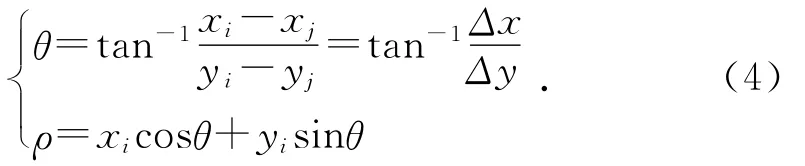
(3)对所有处理后的图像块进行综合处理,从而得到整个图像的变换结果,进而可以检测出原始图像中的直线。
假设原始图像的特征点个数为Ne,整个图像的变换次数为NT,则:

由式(5)可以看出NT和NS近似成反比,NS越大则计算次数越小,但是NS较小时子图较大,所包含的特征点较多,精度较高,计算量也较大。因此当子图块大小取合适的值(如32×32)时,计算量较标准霍夫变换能够大大减少,主要体现在:减少了复杂的三角函数的计算次数、减少了ρ和θ的变化次数、缩小了峰值表决的范围。
3 实际图像处理
本文通过茶叶图片对上述算法在PC上进行测试,所用的硬件环境如下:CPU为AMD,主频为2.10GHz,内存为2GB;软件环境如下:OS为中文Windows,算法程序语言为C++、OpenCV,编译器采用Visual C++6.0。
图4(a)是一幅茶叶和杂质的原始图像,茶叶中夹杂着棍棒类杂质。由于棍棒类杂质包含直线特征,所以利用霍夫直线变换提取出棍棒边缘的直线,达到检测杂质的目的。但是,采集的图像包含着的阴影往往会影响检测结果,因此在霍夫变换之前去除图像阴影显得十分必要。图4(b)是茶叶杂质图片未进行阴影处理而直接利用大津阈值进行二值化,由图4(c)可以看出,图中阴影也被当做前景和背景分离开来了。最后经过霍夫直线检测发现有些直线是茶叶的阴影边缘,显然这些都影响检测效果。图4(d)是经过去阴影处理后的二值图像,再经过霍夫直线检测没有发现由于阴影产生的直线边缘,见图4(e)。实验证明经过去阴影处理后再进行霍夫直线检测能够达到检测具有直线特征杂质(棍棒)的目的。

图4 实验处理结果
为了在不同大小的图片上验证算法,我们采取了两种不同分辨率的图片(1 200×900和400×300),并在多幅图像上做了算法测试。表1是标准Hough变换和改进后的算法处理同一幅图像的平均时间表,算法的角度精度为1°。从表1可以看出,当检测精度为1°时,在相同大小图片情况下,本算法比标准Hough算法快了很多。通过实验证明,本文所提出的算法能很好地检测出具有直线特征的杂质,并且可以减少运算时间,达到理想效果。

表1 角度精度为1°的计算时间表
[1]Illingworth J,Kittler J.A survey of the hough transform[J].CVGIP,1988,44(1):87-107.
[2]Horprasert T,Harwood D,Davis L S.A statistical approach for real-time robust background subtraction and shadow detection[EB/OL].2002-12-15.http://www.cse.lehigh.edu/Frame/Horprasert1
[3]Bevilacua A,Roffilli M.Robust denoising and moving shadows detection in traffic scenes[G]//Proc of IEEE CVPR Technical Sketches Conf.Hawai:[s.n.],2001:1-4.
[4]付萍,方帅,徐心如,等.视频监控系统中运动目标检测的阴影去除方法[J].计算机工程,2007,33(10):22-24.
[5]朱芳芳,顾宏斌,孙瑾.一种改进的Hough变换直线检测算法[J].计算机技术与发展,2009,19(5):19-22.
[6]陈建平,邱力为.基于像素组合的快速哈夫变换[J].计算机工程与应用,2005(22):43-45.
