高仿真直线一级倒立摆模型设计❋

戴源成，张文志

（内蒙古工业大学 机械学院，内蒙古 呼和浩特 010051）

0 引言

倒立摆是非线性、高阶次、多变量强耦合的自不稳定系统，是控制领域经常讨论的问题［1－3］。研究倒立摆一般先要建立倒立摆的数学模型，大多数研究人员建立的倒立摆模型都是理想化的、线性化的，未考虑空气阻力和转轴摩擦力的影响，在这样的模型上开发出来的控制方法应用到真实倒立摆上存在较大的偏差甚至不可行。本文提出了直线一级倒立摆的带有阻力效应的非线性数学模型，重点研究了直线一级倒立摆摆杆在摆动过程中所受到的介质阻力和摩擦力的计算方法，利用Simulink的S函数建立了高仿真非线性虚拟倒立摆，通过调整S函数的相关参数，使虚拟倒立摆与真实倒立摆具有非常接近的工作状态，因而在虚拟倒立摆上获得的结论通常也适用于对应的真实倒立摆。

1 直线一级倒立摆的非线性数学模型

直线一级倒立摆通常由摆杆、摆杆小车及电机伺服系统等组成，其电机伺服系统的输出可分为力矩输出和加速度输出两种形式。采用加速度输出形式时，系统以小车加速度u为输入量，系统模型相对比较简单，因此我们以加速度为输入量来建立系统模型，并假设：摆杆是刚体；摆杆杆长为L；摆杆质心到转轴中心的距离为l；摆杆关于转轴的转动惯量为J；摆杆质量为m。

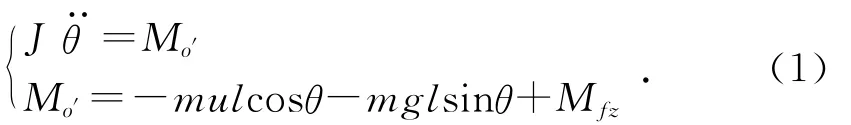
其中：Mo′为作用于摆杆上各外力对转轴的矩；Mfz为阻力fz对转轴的矩，是介质阻力对转轴的矩MJ和转轴摩擦力对转轴的矩Mm的和，Mfz＝MJ＋Mm。

因此摆杆摆角θ和转轴位移x应满足的方程为：

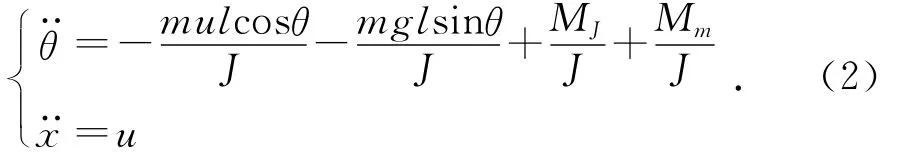
2 倒立摆所受介质阻力的计算

我们提出的介质阻力计算方法基于以下假设：①摆杆迎风面沿摆杆长度方向是均匀一致的；②介质阻力正比于速度的α次方，比例系数为ρ。

现在考虑摆杆角度为θ，摆杆角速度为ω，同时摆杆小车以速度v作水平运动时，摆杆所受的空气阻力，该阻力f可等效为作用于转轴的力f′（f′与f的值相等）和空气阻力对转轴的矩MJ。如图2所示，设A为摆杆转轴中心点，B为摆杆末端端点，在摆杆上任取一点D，设AD的长为s（0≤s≤L），则D点处的迎风速度为：

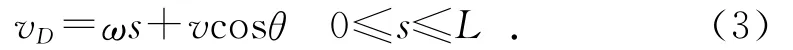
当vD＞0时，表明D点处的迎风速度是顺着θ角正方向的，阻力为负值，反之为逆着θ角正方向的，阻力为正值。为叙述方便，将A，B两点处的迎风速度记为vA和vB，则有：

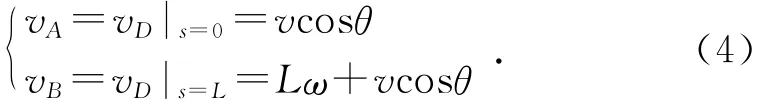
在D点处取一长为ds的摆杆小段（ds很小），该小段所受到的空气阻力为：

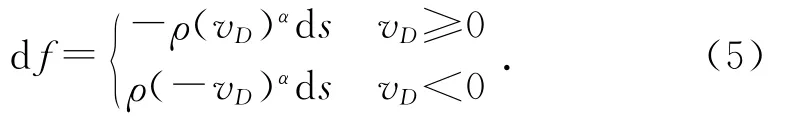
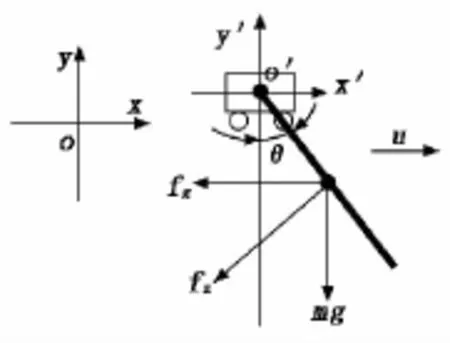
图1 倒立摆系统受力分析

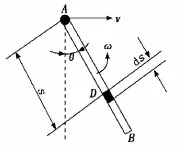
图2 摆杆介质阻力分析

将vD与s关系绘制成直角坐标系下的图形，可得一定义于区间［0，L］上的直线段，我们称它为风速线段。以下根据风速线段的位置分4种情况讨论阻力的计算。

（c）The farmer，whose name was Fred，sold us 10 pounds of potatoes.

（1）vA≥0，vB≥0时，风速线段在s轴上方，摆杆上每一点处迎风速度都不小于0，于是df＝－ρ（ωs＋vcosθ）αds，所以摆杆阻力主矢的大小为：

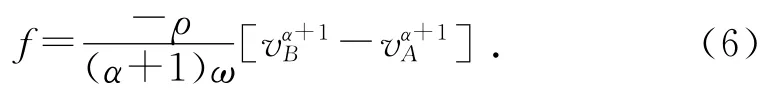
（2）vA≤0，vB≤0时，风速线段在s轴下方，摆杆上每一点处迎风速度都不大于0，于是df＝ρ（－ωsvcosθ）αds，所以摆杆阻力主矢的大小为：

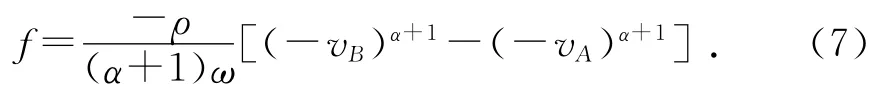
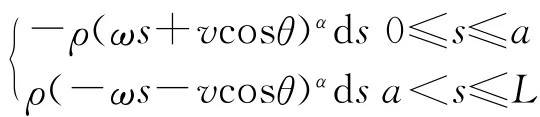
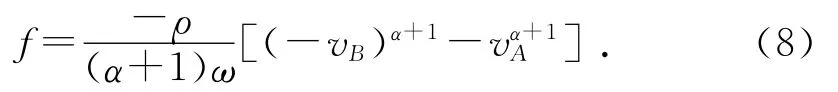
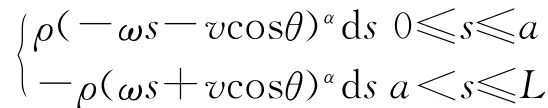
综合上述4种情况的结论，摆杆阻力主矢的大小可整合为一个式子：

空气阻力对摆杆旋转运动的影响表现为空气阻力对摆动旋转轴的矩MJ，同样分4种情况讨论，可得如下结果：

（1）vA≥0，vB≥0时，风速线段在s轴上方，摆杆上每一点处迎风速度都不小于0，于是dMJ＝－ρs（ωs＋vcosθ）αds，所以有：

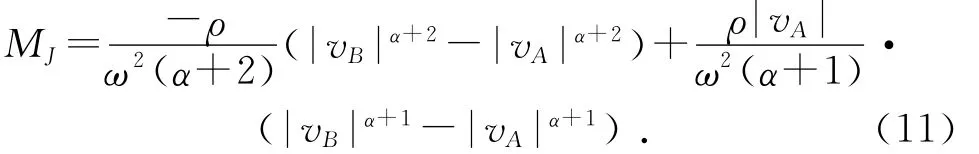
（2）vA≤0，vB≤0时，风速线段在s轴下方，摆杆上每一点处迎风速度都不大于0，于是dMJ＝ρs（－ωsvcosθ）αds，所以有：

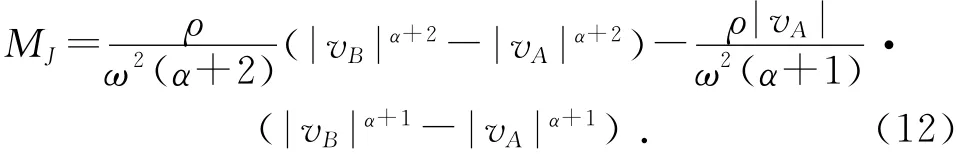
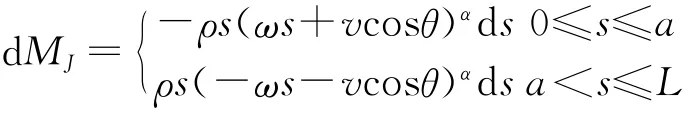
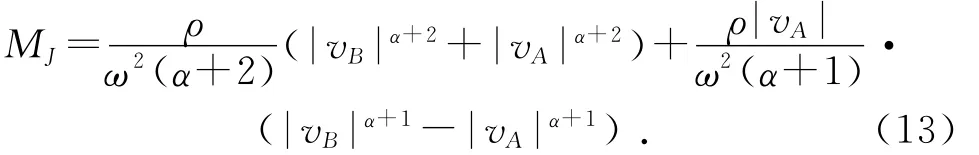
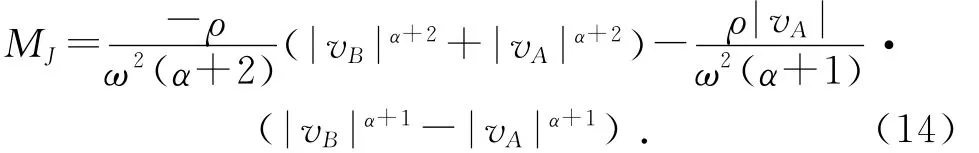
考虑到f和MJ的计算式中，ω出现在分母中，当ω＝0时会出现无法计算的情况，此时可用ω→0时f和MJ的极限值作为ω＝0时的f值和MJ值。

3 倒立摆所受转轴摩擦力的计算

摆杆在摆动过程中，除了受到重力、惯性力和空气阻力等外力作用，还受转轴处摩擦力的作用。为了计算方便，将上节算出的空气阻力f等效为作用于摆杆质心C的力f″（f″与f的值相等）和空气阻力对质心的矩MC，由力线平移原理可得出：

首先我们建立随摆杆一起旋转的直角坐标系如图3所示，Fx和Fy是约束力在两坐标轴上的分量，C（xc，yc）是摆杆质心的坐标，mu是惯性力。转轴处的摩擦力只影响摆杆的旋转运动，因此表现为与约束力成正比的摩擦力矩，设比例系数为λ，则运动微分方程可表示为：

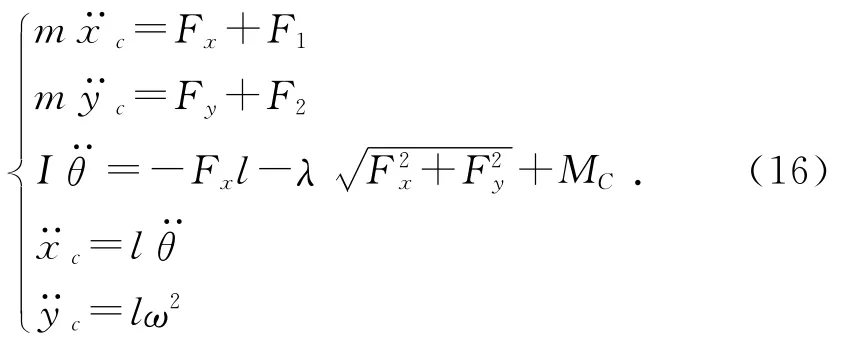
其中：I为摆杆关于过质心且垂直于摆杆的轴的转动惯量；F1和F2分别为各外力在x，y轴上的分量，F1＝－mucosθ－mgsinθ－f，F2＝－musinθ－mgcosθ；为 质 心 切 向 加 速 度；y··c为 质 心 法 向 加 速 度；为摩擦力矩Mm。

因此有：

注意到Fx＋D＜0及μ＞0且很小的事实，上面根式前应取负号。由式（16）和式（17）得到转轴处的摩擦力矩为：

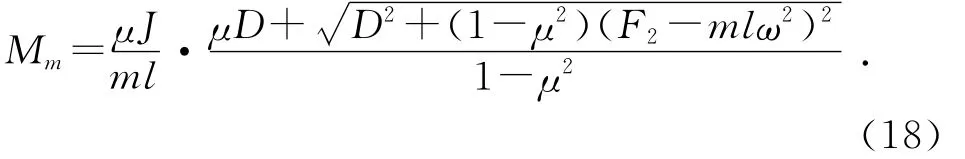
以上是ω＞0时Mm的计算公式，当ω＜0时需在前面添加负号。

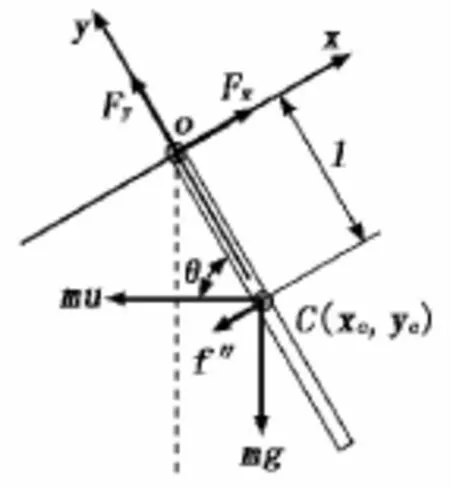
图3 摆杆转轴摩擦力分析

4 高仿真直线一级倒立摆模型的实现

建立高仿真直线一级倒立摆模型的过程如下：①根据直线一级倒立摆满足的微分方程，构造系统的状态方程和输出方程；②利用系统状态方程和输出方程按文献［6］所述方法编写MATLAB的S函数；③按文献［7］所述方法建立倒立摆的虚拟现实模块；④建立上述S函数的相应仿真模块，它有一个加速度输入量和一个输出口，能输出倒立摆工作过程中的小车位移、小车速度、摆杆角度和摆杆角速度；⑤用S函数仿真模块输出的小车位移和摆杆角度驱动虚拟现实模块，再根据需要添加并连接其他仿真模块，就可以非常逼真地进行倒立摆试验或研究了。

图4为倒立摆Simulink仿真试验模型。将虚拟倒立摆的相关参数（如杆长、转动惯量等）设置得与真实倒立摆的完全一致，再调整虚拟倒立摆的摩擦系数λ、空气阻力参数ρ和α，对比虚拟倒立摆与真实倒立摆的状态数据，直至虚拟倒立摆与真实倒立摆的工作状态非常接近。此后就可以在虚拟倒立摆上进行试验和研究。

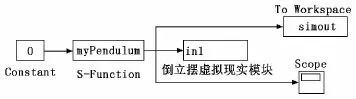
图4 倒立摆Simulink仿真试验模型

我们针对元创兴科技有限公司的便携式直线一级倒立摆，建立了它的仿真倒立摆，经过反复调整，当λ＝0.000 28，ρ＝0.007，α＝1.5时，虚拟倒立摆与真实倒立摆接近得最好。图5为虚拟倒立摆和真实倒立摆的摆杆角度θ的衰减曲线，虽然通过局部放大的子图可以看出两曲线间的细微差别，但整体看来两曲线几乎是重叠的。

图5 模拟倒立摆与真实倒立摆的摆角衰减曲线

［1］Yi J，Yubazaki N.Stabilization fuzzy control of inverted pendulum system［J］.Artficial Intelligence in Engineering，2000（14）：153-163.

［2］Chen Shi-Yuan，Yu Fang-Ming，Chung Hung-Yuan.Decoupled fuzzy controller design with single-input fuzzy logic［J］.Fuzzy Sets and Systems，2002，129：335-342.

［3］Suykens J A K，Vandewalle J，Moor B De.Optimal control by least squares support vector machines［J］.Neural Networks，2001，14：23-35.

［4］周衍柏.理论力学教程［M］.第3版.北京：高等教育出版社，2009.

［5］浙江大学理论力学教研室.理论力学［M］.第3版.北京：高等教育出版社，1999.

［6］谭智，李祖枢.加速度控制的倒立摆的S函数建模［J］.重庆理工大学学报（自然科学版），2013，27（6）：53-57.

［7］徐林，高巍，邱联奎.基于VRML的倒立摆三维仿真［J］.计算技术与自动化，2009，28（3）：24-26.