一类满足绝热逼近的量子态存在性及其结构

余保民，郭志华

（1渭南师范学院 数学与信息科学学院，陕西 渭南 714000；2陕西师范大学 数学与信息科学学院，陕西 西安 710062）

绝热定理的研究最早是由Ehrenfest提出，他用早期的量子理论研究了绝热过程［1－4］，1928年，Born和Fock把它推广到量子力学波动方程，用现代量子力学理论给出了其证明［5］，在文献［6］中，作者用数学方法给出绝热定理的严格证明.1984年，Berry在研究绝热定理时发现了一个可被观测的新的几何相位［7］，引起了物理学界的极大兴趣.文献［8］用Hamiltonian随时间的变化率对系统的“缓慢变化”定量刻画，给出绝热定理的更为精确的表述，并对Berry相位和 Wilczed-Zee算符的导出做了简化.在文献［9］中，作者把绝热演化中的Beery相位推广到包括非本征态的一般量子态.迄今为止，关于绝热定理的讨论仍是一个研究的热点［10－15］.基于绝热逼近的方法，绝热定理在物理学、化学等很多领域有广泛的应用，例如分子物理中的Landau-Zener转换［15］、量子场论［16］、几何相位、绝热量子计算及新的量子算法等［17－20］.本文根据文献［21］中对绝热逼近中“缓慢演化”＇充分条件的结果，证明满足这一充分条件的量子态的存在性，并详细讨论这种单量子比特态的构造.

1 预备知识

比特（bit）是经典计算和经典信息的基本概念.量子计算中的基本单位是量子比特.正如经典比特有一个状态0或1，量子比特也有一个状态，量子比特的两个可能状态是

以上符号｜·〉称为Dirac记号.〈·｜为｜·〉的共轭转置.经典比特和量子比特的区别在于经典比特的状态只能是0或1，而量子比特的状态可以落在0和1之外，即它可以是状态｜0〉与｜1〉的线性组合，通常称之为叠加态（superposition），记为｜ψ〉＝α｜0〉＋β｜1〉，其中α和β是复数且｜α｜2＋｜β｜2＝1，即量子比特的状态是二维复向量空间中的任意单位向量.特别地，｜0〉和｜1〉状态称为计算基态（computational basis state），是构成量子比特状态空间的一组标准正交基.

根据量子力学中假设:任一孤立量子系统都由一个Hilbert空间来描述，称之为系统状态空间，系统完全由系统空间中的单位向量（称为状态向量）所描述.封闭量子系统的演化由Schrödinger方程

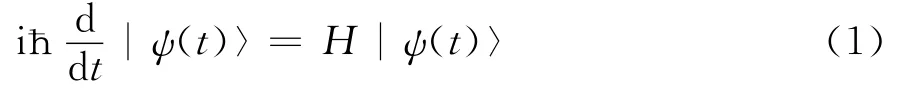
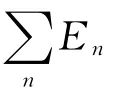
作为量子力学中最古老的定理之一［1，6］，绝热定理告诉我们:如果系统在某一时刻的状态处于“缓慢演化”的Hamiltonian的瞬时本征态，那么在之后的演化时间中，系统的状态仍然近似于这一本征态（相差一个相位因子）［7］.用数学的语言叙述，即对一个HamiltonianH（t）依赖于时间t的量子系统，用En（t）和｜En（t）〉分别表示H（t）的瞬时本征值和对应的瞬时本征态.如果｜ψ（t）〉是Schrödinger方程（1）在［0，T］的一个解，且｜ψ（0）〉＝｜En（0）〉，那么当H（t）在［0，T］内演化的足够“缓慢”时，存在实值函数θn（t），使得｜ψ（t）〉＝eiθn（t）｜En（t）〉对任意的t∈ ［0，T］成立.

文献［21］研究HamiltonianH（t）可以“缓慢演化”的充分条件时，证明了以下定理:

设｜ψ（t）〉为Schrödinger方程（1）的解且满足初始条件｜ψ（0）〉＝｜En（0）〉.如果

由此可知:如果

那么1－｜〈ψ（t）｜En（t）〉｜＜ε，∀t∈ ［0，∞）.进而，系统（1）在任一时刻的状态｜ψ（t）〉可以用本征态｜En（t）〉在整个时间区间［0，∞）上一致逼近，其误差一致小于ε.这说明条件（3）是一致绝热逼近的一个量化充分条件.本文讨论满足条件

的量子态｜f（t）〉的存在性及其结构，进而构造其本征态｜En（t）〉满足（3）的 HamiltonianH（t）.

2 单量子比特态的情形

令｜f（t）〉是带有参数t的单比特态（关于t的二维复向量值函数）.以下讨论满足条件（4）的单量子比特态的结构.

定理1 设｜f（t）〉＝ （eiα（t）sinx（t），eiβ（t）cosx（t））T是连续可微的单量子比特态，则（4）成立当且仅当

（ⅰ）∀t≥0，有

证明 计算可知 ∀t≥0，〈f（t）｜f′（t）〉＝i（α′（t）sin2x（t）＋β′（t）cos2x（t）），

令A（t）＝｜x′（t）cosx（t）＋iα′（t）sinx（t）｜2＋｜－x′（t）sinx（t）＋iβ′（t）cosx（t）｜2，则

必要性 设（4）成立.由〈f（t）｜f′（t）〉＝0（t∈ ［0，∞））知i（α′（t）sin2x（t）＋β′（t）cos2x（t））＝0（t∈ ［0，∞））.

当α′（t）＝β′（t）时，

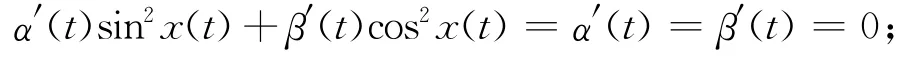
当α′（t）≠β′（t）时，

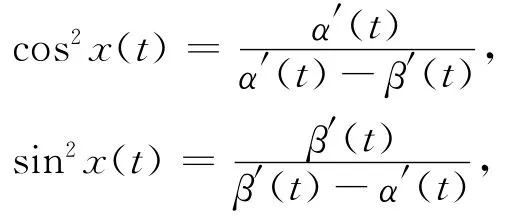
所以（5）式成立.进一步，由（6）式得

从而有

推论1 ｜f（t）〉＝ （eiα（t）sinx（t），eiβ（t）cosx（t））T是连续可微的单量子比特态，则当｜x′（t）｜dt≥ε或时，（4）不成立.

定理2 设｜f（t）〉是连续可微的单量子比特态，则

（ⅰ）当｜f（t）〉与时间t无关时，｜f（t）〉一定满足条件（4）式；

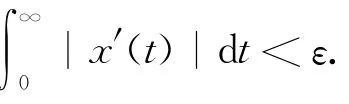
证明 （ⅰ）显然.

（ⅱ）当｜f（t）〉＝ （aeiα（t），beiβ（t））T时，计算可知｜f′（t）〉＝ （aα′（t）eiα（t），bβ′（t）eiβ（t））T，并有

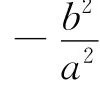
再由（7）式知〈f（t）｜f′（t）〉＝i（a2α′（t）＋b2β′（t））＝0，因此，条件（4）成立.

（ⅲ）当｜f（t）〉＝ （eiαsinx（t），eiβcosx（t））T时，易 知 ｜f′（t）〉＝ （eiαx′（t）cosx（t），－eiβx′（t）sinx（t））T，〈f（t）｜f′（t）〉＝0（∀t∈ ［0，∞））.这时

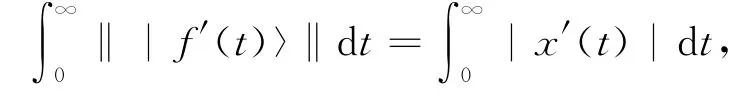
注1 定理1和定理2也给出了满足（4）式的单量子比特态的具体结构形式.

3 n维系统的情形

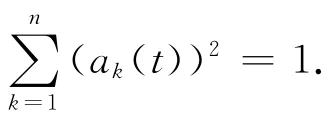
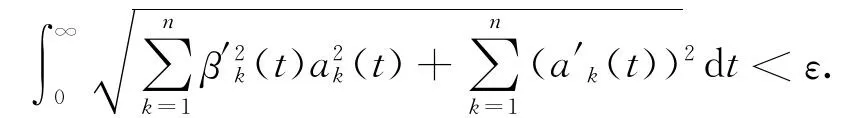
证明 计算可知:∀t≥0，有

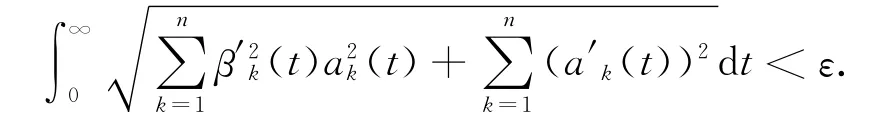
对任意的t≥0，令

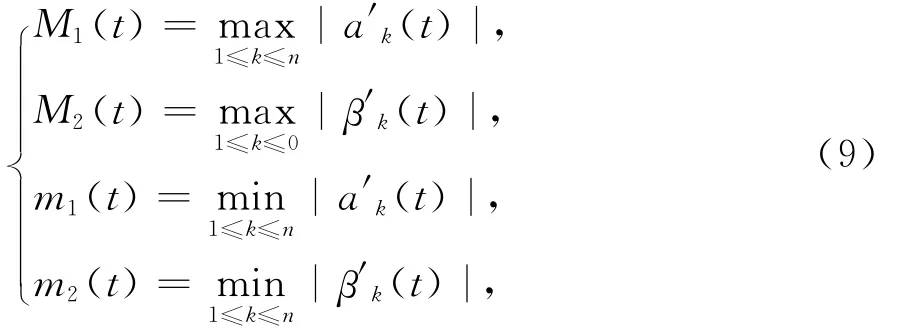
则由（8）知

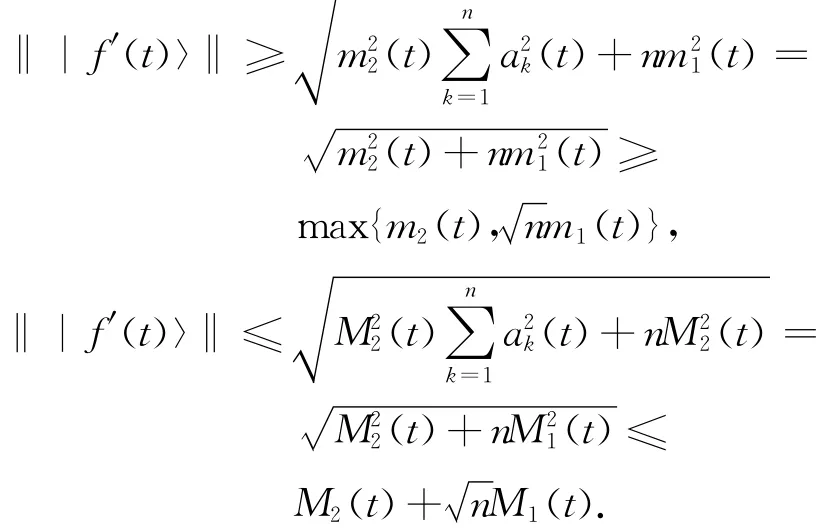
由此可得

例1 设一个量子系统的HamiltonianH（t）具有如下形式:

满足定理1的条件，进而满足文献［21］中HamiltonianH（t）可以“缓慢演化”的充分条件.

4 结语

［1］Griffiths D J.Introduction to quantum mechanics［M］.2nd ed.Upper Saddle River:Prentice Hall，Inc，1995.

［2］李华钟.量子绝热定理，思想和方法［J］.物理，2005，34（6），418-423.

［3］李华钟.量子绝热定理（Ⅱ）:近似和适用条件［J］.物理，2007，36（1）:26-31.

［4］曾谨言.量子物理学百年回顾［J］.物理，2003，32（10）:665-672.

［5］Born M，Fock V.Beweis des adiabatensatzes［J］.Zeitschrift für Physik，1928，51:165-180.

［6］Kato T.On the adiabatic theorem of quantum mechanics［J］.Journal of the Physical Society of Japan，1950，5:435-439.

［7］Berry M V.Quantal phase factors accompanying adiabatic changes［J］.Proceedings of the Royal Society of London.A.Mathematical and Physical Sciences，1984，392:45-57.

［8］李伯臧，吴建华.绝热定理表述的改进以及Berry相位和 Wilczed-Zee算符导出的简化［J］.物理学报，1995，44（1）:16-23.

［9］吴飙，刘杰.绝热演化中的一般量子态的几何相位［J］.物理，2005，34（12）:883-886.

［10］Guo chu，Duan qianheng，Chen pingxing.A new approcach to the quantum adiabatic condition［J］.Chinese Physics Letters，2012，29（10）:100301（1-4）.

［11］Rigolin G，Ortiz G.Adiabatic theorem for quantum systems with spectral degeneracy［J］.Physical Review A，2012，85:062111（1-4）.

［12］Viennot D，Leclerc A，Jolicard G emph，et al.Consistency between adiabatic and non-adiabatic geometric phases for non-self-adjoint Hamiltonians［J］.Journal of Physics A:Mathematical and Theoretical，2012，45:335301（1-8）.

［13］雷奕安，曾谨言.Berry相与AB相位的关系［J］.物理学报，1997，46（1）:19-21.

［14］曾谨言.有关A-B效应和相伴问题及量子绝热定理成立条件［J］.大学物理，2006，25（8）:29-32.

［15］Wubs M，Saito K，Kohler S，et al.Gauging aquantum heat bath with dissipative Landau-Zener transitions［J］.Physical Review Letters，2006，97:200404（1-4）.

［16］Gell-Mann M，Low F.Bound states in quantum field theory［J］.Physical Review，1951，84:350-354.

［17］Farhi E，Goldstone J，Gutmann S，et al.A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem［J］.Science，2001，292:472-475.

［18］Siu M S.From quantum circuits to adiabatic algorithms［J］.Physical Review A，2005，71:062314-062320.

［19］郑淮斌，仇旭，李永放.绝热条件下二能级系统相干控制动态分析［J］.陕西师范大学学报:自然科学版，2007，35（4）:28-32.

［20］田巍，姚建永，王渭娜，等.胺基自由基绝热电离能的理论计算研究［J］.陕西师范大学学报:自然科学版，2009，27（2）:60-63.

［21］Cao Huaixin，Guo Zhihua，Chen Zhangli，et al.Quantitative sufficient conditions for adiabatic approximation［J］.Science China:Physics，Mechanics ＆ Astronomy，2013，56（7）:1401-1407.