非线性偏微分方程组的广义变量分离解

郝夏芝，姚若侠

（陕西师范大学 计算机科学学院，陕西 西安 710062）

不变子空间方法是求解非线性偏微分方程（组）广义变量分离解的有效方法之一［1－2］，该方法受到广泛关注是基于一般高维非线性偏微分方程通常拥有变量分离解这一事实。一个偏微分系统所允许的不变子空间一般包含多项式函数、指数函数以及三角函数等类型.利用不变子空间方法求解非线性偏微分方程的关键是利用线性常微分方程解的子空间来构造偏微分方程和方程组所允许的不变子空间.本文以非线性偏微分方程组为例，通过不变子空间方法求解它的若干广义变量分离解.

1 不变子空间方法

一般来说，人们可以通过不变子空间方法来获取各种特殊的非线性偏微分方程（组）的广义变量分离解，继而对其诸多性质展开研究［3－8］.利用不变子空间方法求解非线性偏微分方程广义变量分离解的一般步骤如下:

步骤1 确定非线性偏微分方程的不变子空间.

考虑一般的非线性偏微分方程:ut＝F［u］.F［u］表示最高阶为k阶的非线性微分算子.令n维不变子空间Wn＝L｛f1（x），…，fn（x）｝，集合中的各个元素fi（x）（i＝1，…，n）相互独立，且由n阶常微分方程

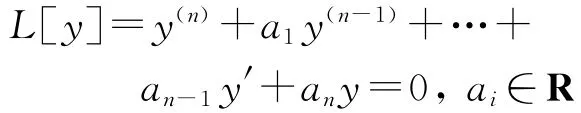
在满足特定不变条件时得到.不变子空间的维数n满足关系n≤2k＋1，k为微分算子F［u］的阶数［3，8］.这里所说的不变条件为L［F［u］］｜L［u］＝0≡0，即算子F［u］允许n维不变子空间

此外，如果在算子F［u］的作用下，有F［Wn］⊆Wn，子空间Wn即被认为是不变的.那么，Wn是算子F［u］所允许的不变子空间.

步骤2 构造非线性偏微分方程的广义变量分离解.

一旦不变子空间被确定，方程所允许的广义变量分离解即可记为

其中，Ci（t）（i＝1，…，n）为待定函数.若方程允许该形式的广义变量分离解，则有

其中，系数｛Ci（t）｝满足n维动力系统

求解该动力系统可确定u（x，t）中所有的待定函数，继而可获得非线性偏微分方程的广义变量分离解.

2 方程组的广义变量分离解

下面以非线性偏微分方程组为例来演示如何确定它所允许的不变子空间及其广义变量分离解.考虑如下形式的非线性偏微分方程组:

其中αi、βi（i＝1，2，3）为常数，F、G表示非线性微分算子.u、v是关于x、t的函数，下标x、t表示函数u、v关于它们的偏导数.

假设方程组所允许的不变子空间由2个二维子空间构成，即W2，2＝×，且W2，2由如下常微分方程组定义:

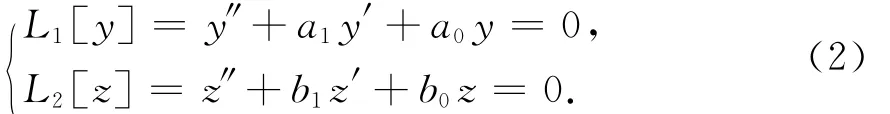
其中a0、a1、b0、b1为待定常数.由步骤1可知，方程组（1）允许不变子空间W2，2当且仅当满足不变条件

其中D是全微分算子.分别把（1）中的两个等式F（u）、G（u）代入（3）中相应的方程，并替换所有的二阶导数项，即反复用－a1ux－a0u替换uxx，用－b1vx－b0v替换vxx.对替换后的表达式合并同类项，整理可得包含项、uux、vx、vxux、vux、vxu和vu的方程，令其系数为零，可得关于（1）和（2）中未知系数的决定方程组:

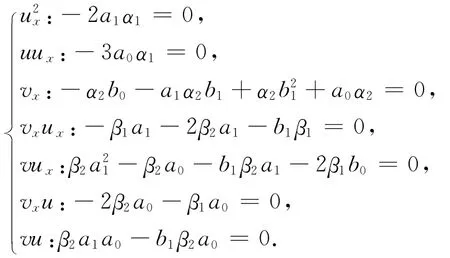
借助符号计算软件Maple求解该代数方程组，可得到关于系数αi、βi、a0、a1、b0、b1（i＝1，2，3）之间的约束条件，继而可获得方程组（1）的广义变量分离解.不同约束条件下获得的方程组的不变子空间类型不同.子空间类型虽然不同，但求解过程类似，所以本文仅选取具有代表性的两种情形来分析方程组（1）的解.

解1 第一组参数约束条件为

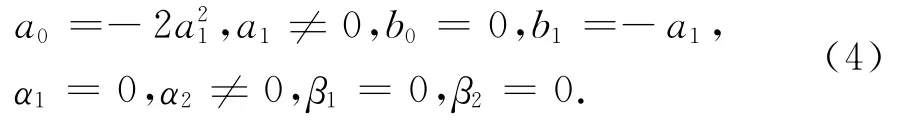
把（4）中的关系式分别代入（1）和（2）可得

求解（6）可获得方程组（5）的不变子空间

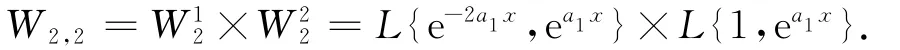
那么，方程组（5）允许广义变量分离解

其中，C1、C2、D1、D2是t的函数.将（7）式代入方程组（5）中可知C1、C2、D1、D2满足动力系统

求解动力系统（8），可得两组不同的解:

（Ⅰ）当α3＝β3，方程组（8）有解

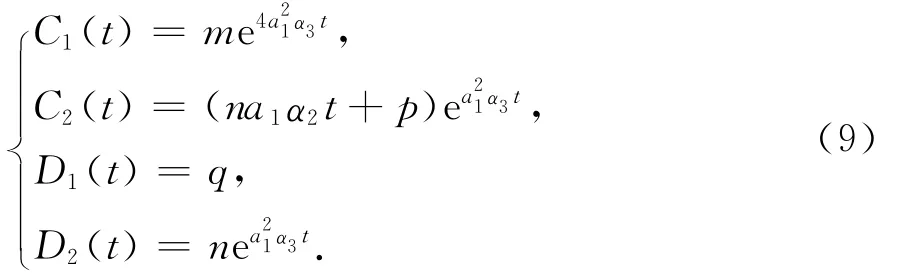
将C1、C2、D1、D2的值代入（7）中，可得方程组（5）的广义变量分离解

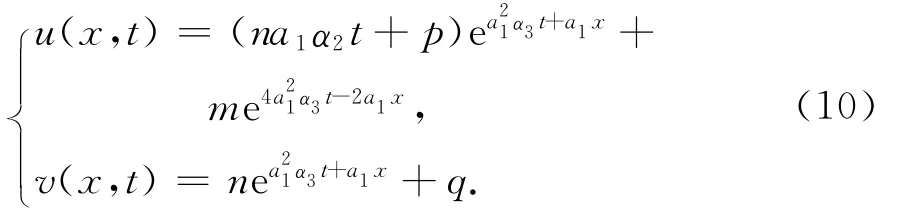
解的图形可直观地帮助人们分析解的演化、局部渐近及其爆破行为.不妨取（10）中的常数分别为a1＝1、α2＝1、α3＝1、m＝1、n＝1、p＝0、q＝0，则解的三维图形如图1和图2所示.

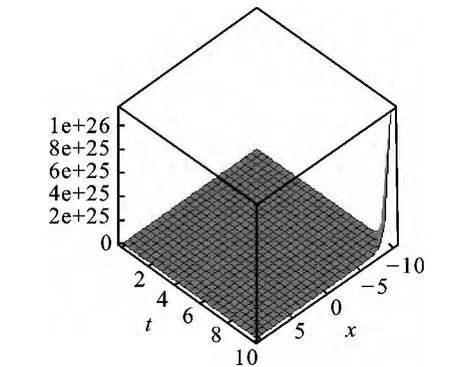
图1 解u（x，t）＝e4t－2x＋tet＋x 的三维图Fig.1 3Dgraph of the solution of u（x，t）＝e4t－2x ＋tet＋x

图2 解v（x，t）＝et＋x 的三维图Fig.2 3Dgraph of the solution of v（x，t）＝et＋x

（Ⅱ）当α3≠β3，方程组（8）有解

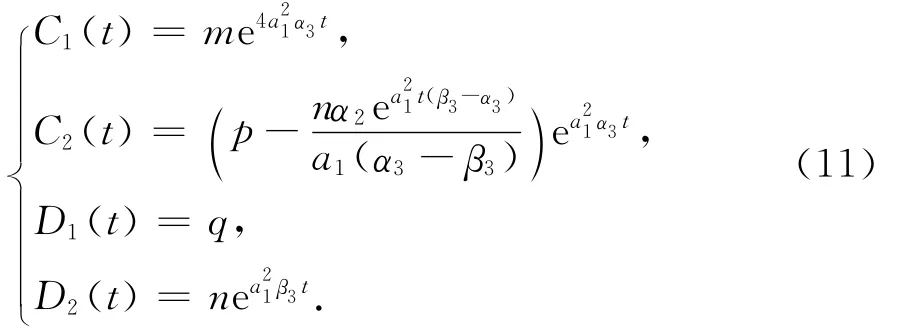
其中，m、n、p、q均为任意常数.将（11）中的值代入（7）中，得到方程组（5）的广义变量分离解

给定解（12）中的常数值，则同样可画出其三维图形，此处不再列出.

解2 第二组参数约束条件为

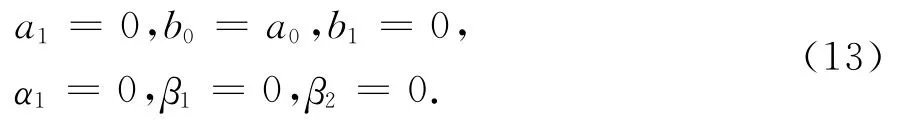
把（13）中的值分别代入方程组（1）和（2）可得

显然，a0的取值会影响方程组（15）解的形式，即方程组（14）的子空间会随着a0的取值而变化，a0可分别取正值、负值和零.那么，在二维不变子空间下，方程组（15）解的类型可分别为三角函数、指数函数或多项式函数这3种情形.相应地，方程组（14）的不变子空间也为这3种类型.下面分别予以讨论.

（Ⅰ）当a0＞0，不妨令a0＝4，求解方程组（15）可得类型为三角函数的不变子空间

则方程组（14）的广义变量分离解为

将解（16）代入（14），可知C1、C2、D1、D2满足动力系统

求解该动力系统可得两组解:

（ⅰ）当α3≠β3，方程组（17）有解

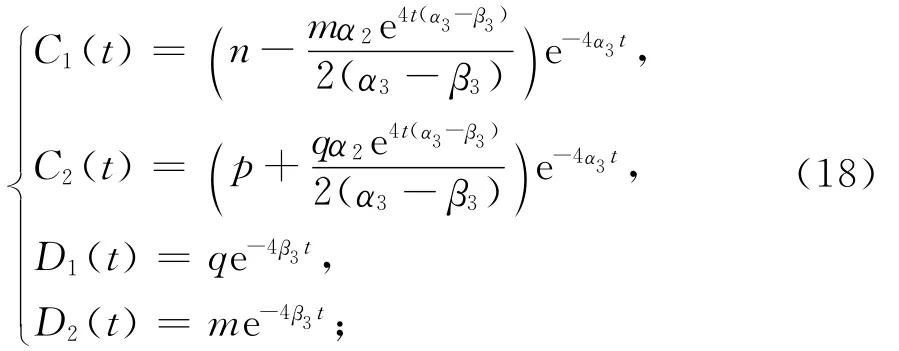
（ⅱ）当α3＝β3，方程组（17）有解

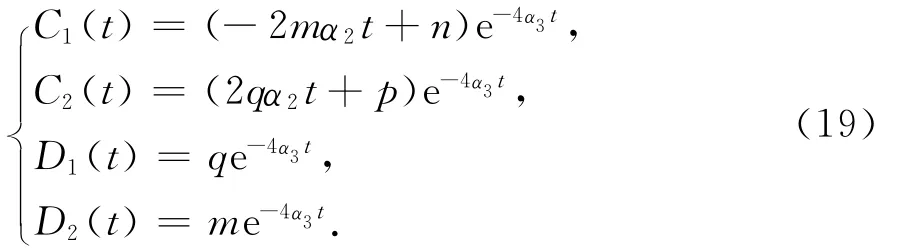
将（18）和（19）中C1、C2、D1、D2的值分别代入方程组（16），可获得方程组（14）的两组解，解的具体形式文中不再列出.

（Ⅱ）当a0＝0，求解（15）可获得多项式类型的不变子空间

那么，方程组（14）的变量分离解为

将解（20）代入（14），可知C1、C2、D1、D2满足动力系统

求解动力系统（21）可得

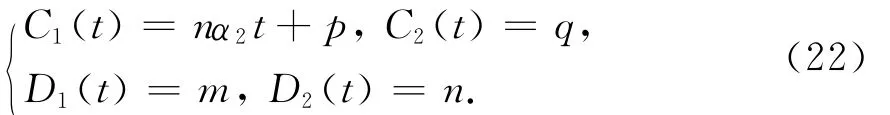
同样，将（22）中C1、C2、D1、D2的值代入方程组（20）即可获得方程组（14）的解.

（Ⅲ）当a0＜0，不妨令a0＝－4，求解（15）得到类型为指数函数的不变子空间

于是，方程组（14）的广义变量分离解为

将解（23）代入（14）中，可知C1、C2、D1、D2满足动力系统

求解该动力系统可得

（ⅰ）当α3≠β3，方程组（24）有解

（ⅱ）当α3＝β3，方程组（24）有解

至此，将（25）和（26）分别代入方程组（23）中，即可获得方程组（14）的另外两种广义变量分离解.解的具体形式和图形文中不再列出.

3 结语

本文在假设不变子空间为二维的前提下，基于符号计算系统Maple，利用不变子空间方法构造了一个具有未知系数的非线性偏微分方程组的若干广义变量分离解.研究表明，当未知系数之间满足不同的约束关系时，可以得到一系列不同形式的解.如正文所述，解1中方程组的子空间是唯一确定的，而解2中方程组的子空间则是由方程（15）中的不同参数值所确定，对应的解因而也各不相同.此外，该非线性偏微分方程组的解不局限于文中所列出的.事实上，可以将不变子空间扩展为更高维的，由此便可获得形式更为丰富的广义变量分离解.

［1］Qu Changzheng，Zhu Chunrong.Classification of coupled systems with two－component nonlinear diffusion equations by the invariant subspace method［J］.Journal of Physics A:Mathematical and Theoretical，2009，42（47）:475201（1-27）.

［2］Ma Wenxiu.A refined invariant subspace method and applications to evolution equations［J］.Science China Mathematics，2012，55（9）:1769-1778.

［3］Galaktionov V A，Svirshchevskii S R.Exact solutions and Invariant subspace of nonlinear partial differential equations in mechanics and physics［M］.London:Chapman and Hall/CRC，2007.

［4］Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities［J］.Proceedings of the Royal Society of Edinburgh:Section A Mathematics，1995，125 （2）:225-246.

［5］姬利娜，冯玮.带源的非线性扩散方程的精确解［J］.纯粹数学与应用数学，2010，26（5）:725-727.

［6］姬利娜，冯玮.非线性扩散方程的广义分离变量解［J］.西北大学学报:自然科学版，2011，41（4）:587-592.

［7］Svirshchevskii S R.Invariant linear spaces and exact solutions of nonlinear evolution equations［J］.Nonlinear Mathematical Physics，1996，3（1/2）:164-169.

［8］Zhu Chunrong，Qu Changzheng.Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators［J］.Journal of Mathematical Physics，2011，52（4）:043507-1-043507-15.