改革开放以来中国农业投入产出水平定量研究——一种基于灰色优势分析的研究方法
2014-12-31李丽纯
李丽纯
(中共长沙市委党校,湖南 长沙 410004)
一、问题的提出
农业投入产出问题的一般研究思路是:首先从一系列农业产出指标和投入指标中分别提取出若干关键指标,然后利用这些关键指标的时间序列数据或空间序列数据进行投入产出模型的回归分析,最后利用估计得出的农业生产函数进行有关解释和预测分析。依据农业产出指标是否多元化,此类研究又可划分为两种类型:一是“单产出指标、多投入指标”的研究,较典型的有:冯子华、覃炳英(1994)把农业总产值作为单一产出指标,依据1977-1992 年的数据对海南省的农业生产函数模型进行了估计[1];林玉蕊(2007)把农业总产出作为单一产出指标,依据1994-2005 年的数据估算了福建省的农业C-D 生产函数模型[2];张立超、瞿印礼(2010)把粮食总产量作为单一产出指标,采用多元线性回归模型,依据1996-2008 年的数据对我国31 个省(市、区)的农业投入产出关系逐一进行了回归分析[3]。二是“多产出指标、多投入指标”的研究,较典型的有:史明瑛、朱云鹃(1999)把农业总产值、粮食总产量2 项作为农业产出指标,运用逐步回归法研究了1970-1997 年安徽省的农业投入产出变动关系及影响因素[4];陈健芬(2011)把农业总产值、农业劳动生产率2 项作为农业产出指标,运用普通最小二乘法研究了我国沿海发达地区的财政农业投入的产出弹性[5];冯启磊等(2010)把总产出水平、人均产出水平、产出增长水平3 项作为产出指标,运用典型相关性分析法研究了我国1990-2007 年的农业投入产出关系[6];王学超(2009)把粮食产量、棉花产量、油料产量、水果产量4项目作为农业产出指标,运用主成分分析法针对2005 年的省际数据进行了投入产出的回归分析[7]等。
上述研究虽然都在一定程度上揭示了我国农业投入和产出之间大致的“数量关系”,但仍不能充分揭示农业投入和产出的“数量水平”,尤其缺少对这种“数量水平”在时间序列方向的波动趋势分析。因此笔者以为,要想全面准确地把握我国农业生产的发展规律,不仅需要研究农业投入产出的关系,而且需要研究农业投入产出的水平。具体地讲,农业投入产出水平可以从两个方面进行衡量,一是农业投入产出的规模,即农业的总体投入规模和总体产出规模,侧重考查农业投入产出“量”;二是农业投入产出的效益,即农业产出相对于农业投入的溢出水平,侧重考查农业投入产出的“质”。
实际上,科学测评农业投入产出水平需要重点解决好两个问题:一是评价指标的选取,一般应坚持系统性、综合性、重点性、代表性和可比性等原则[7]。二是评价指标权重的确定,主要应坚持客观性原则,即在算法设计上要尽可能地排除主观因素的干扰。从既有文献来看,对于评价指标的合理选取问题,不少学者已经分别运用聚类分析法、主成分分析法和因子分析法等方法进行了较好的优化,基本形成了一个相对稳定和普适的农业投入产出评价指标群;但对于评价指标的赋权,目前学界普遍采用的德菲尔法、层次分析法和典型相关性分析法,由于存在较明显的主观假定,在相当程度上影响了农业投入产出指数的可信度。
本文的基本思路是:首先通过对既有文献成果的综合比较,主要基于重要性和可行性原则,选取若干能够有效衡量农业产出水平和农业投入水平的评价指标,构建农业投入产出水平评价指标体系;然后运用灰色优势分析法,在基本排除主观因素干扰的条件下确定各评价指标的权重;最后对1982-2011年中国的农业投入产出指数进行测度分析。
二、农业投入产出水平评价指标的选取与赋权
1.农业投入产出水平评价指标的选取
由于本文研究的重点是农业投入产出的“水平”而非“关系”,所以与一般针对农业投入产出关系的回归分析不同,并不一定要求排除所选指标之间的共线性问题。本文在参考借鉴既有相关研究成果的基础上,直接选取劳均农业产值等5 个指标作为农业产出指标,选取农业机械投入等7 个指标作为农业投入指标,构建中国农业投入产出水平评价指标体系,各指标的定义和计量说明见表1。
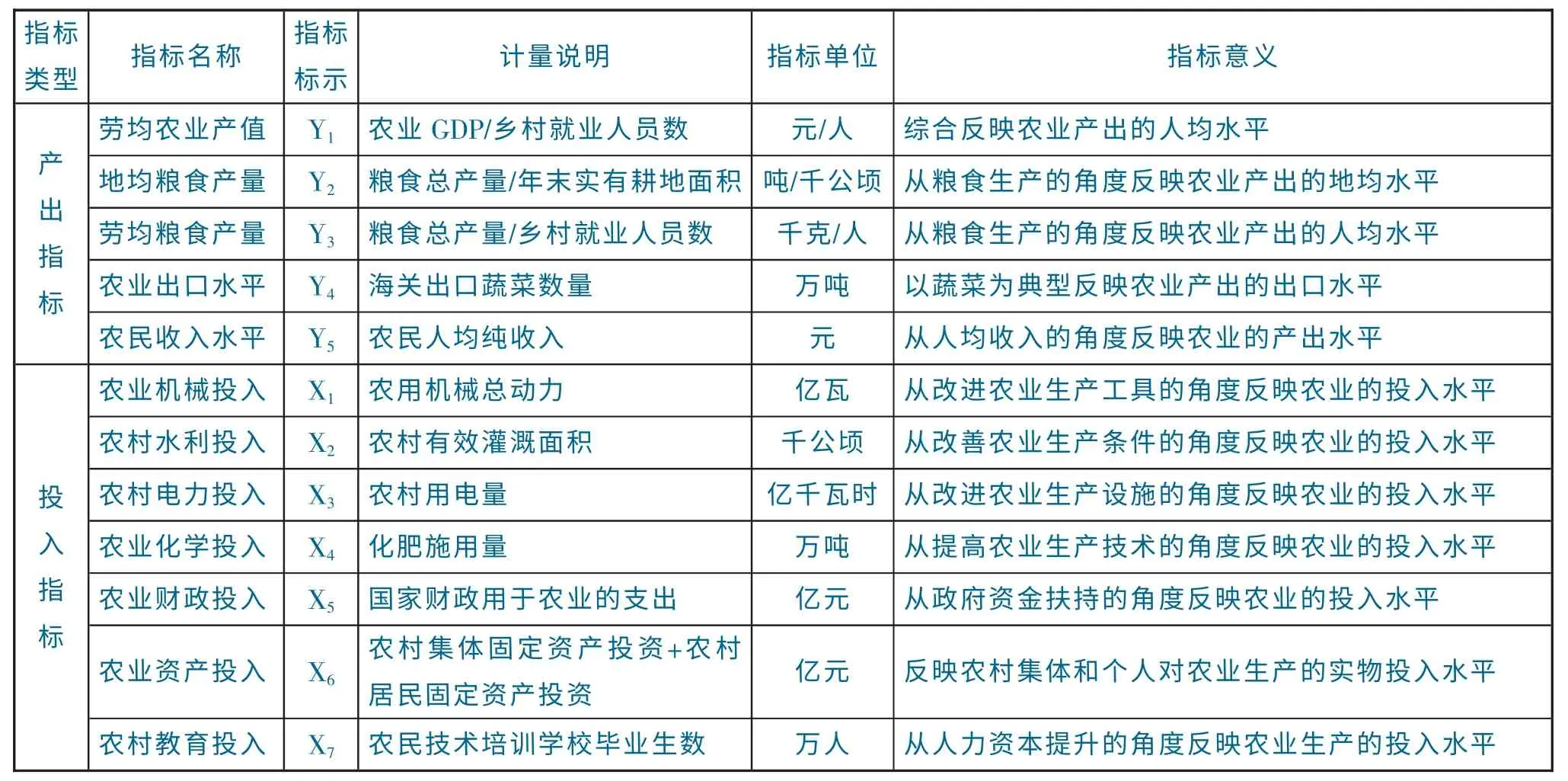
表1 中国农业投入产出水平评价指标体系
2.农业投入产出水平评价指标的赋权
灰色系统理论自1982 年由我国华中科技大学邓聚龙教授首次提出以来,因其能够借助几何方法有效解决“小样本、贫信息”的变量分析问题,在工业、农业、生态、经济、社会、生物等多个学科领域中得到广泛应用[8]。灰色优势分析的基本原理是:对于某个系统中具有因果关系的两组行为序列,可以通过计算它们之间的灰色关联矩阵,分别得出系统中的优势特征排序和优势因素排序[9]。本文则在此基础上更进一步,把这种优势排序的量化处理结果,作为各行为序列在系统评价指标体系中的赋权依据。与一般的多元统计分析中的关键因素分析法相比较,此法的最大优势在于不用事先假定各序列间存在某种特定的函数关系,从而基本克服了指标赋权时的主观因素干扰,提升了整个评价体系的可信度。
(1)收集整理评价指标的实际值。上述12 个评价指标共涉及14 个统计数据指标,其中绝大部分数据可以通过查阅1985-2012 年《中国农村统计年鉴》和1982-2011 年《国民经济和社会发展统计公报》获取,对于个别缺失数据,采用线性插值法进行估算(1982-2011 年中国农业投入产出评价指标的实际值见附表1)。
(2)计算评价指标的灰色综合关联矩阵。把Y1,Y2,…,Y5作为农业投入产出系统的特征行为序列,X1,X2, …,X7作为农业投入产出系统的相关因素行为序列,基于刘思峰等在《灰色系统理论及其应用(第五版)》中提出的“优势分析”原理[10]P5,利用“灰色系统理论建模系统3.0”软件,将前述收集整理得到的农业投入产出水平评价指标实际值代入计算,可得中国农业投入产出水平评价指标灰色综合关联度矩阵:
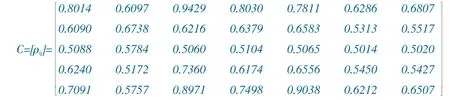
其中ρij为指标Yi与指标Xj的灰色综合关联度(i=1,2,…,5; j=1,2,…,7),且第i 行元素为指标Yi(i=1,2,…,5)与农业投入产出系统各相关因素指标的灰色综合关联度,第j 列元素为指标Xj(j=1,2,…,7)与农业投入产出系统各特征指标的灰色综合关联度。
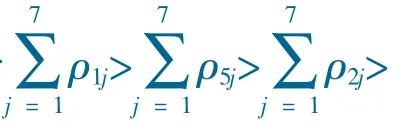
(4)依据灰色综合关联矩阵计算评价指标的权重。令Ui和Vj分别表示指标Yi和指标Xj的权重(i=1,2,…,5; j=1,2,…,7),且
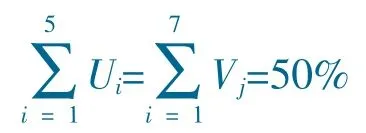

表2 基于灰色优势分析的中国农业投入产出水平评价指标赋权结果
三、中国农业投入产出指数测度与波动趋势分析
1.农业投入产出水平评价指标数据的标准化
设Z=(z1,z2,…zn)为系统因素Z 的行为序列,若算子D 满足:ZD=(z1d,z2d,…znd),其中zkd=(zkminzk)/(maxzk-minzk),k=1,2,…,n,则称ZD 为Z 在区间值化算子D 下的像。
运用区间值化算子D 把1982-2011 年中国农业投入产出水平评价指标的实际值YD 转换为标准值,从而消除了各评价指标数据的量纲差异(1982-2011 年中国农业投入产出水平评价指标的标准值见附表2)。
2.按标准值加权平均得出农业投入产出指数
依据前述中国农业投入产出水平评价指标赋权和1982-2011 年中国农业投入产出水平评价指标的标准值,可计算得出衡量中国农业投入产出水平的四类指数(见表3),各类指数的具体计算公式如下:
K=1982,1982,…,2011;
K=1982,1982,…,2011;
(3)农业投入产出规模指数(M1):M1K=CK+TK,
K=1982,1982,…,2011;
(4)农业投入产出效益指数(M2):M2K=CK-TK,
K=1982,1982,…,2011。
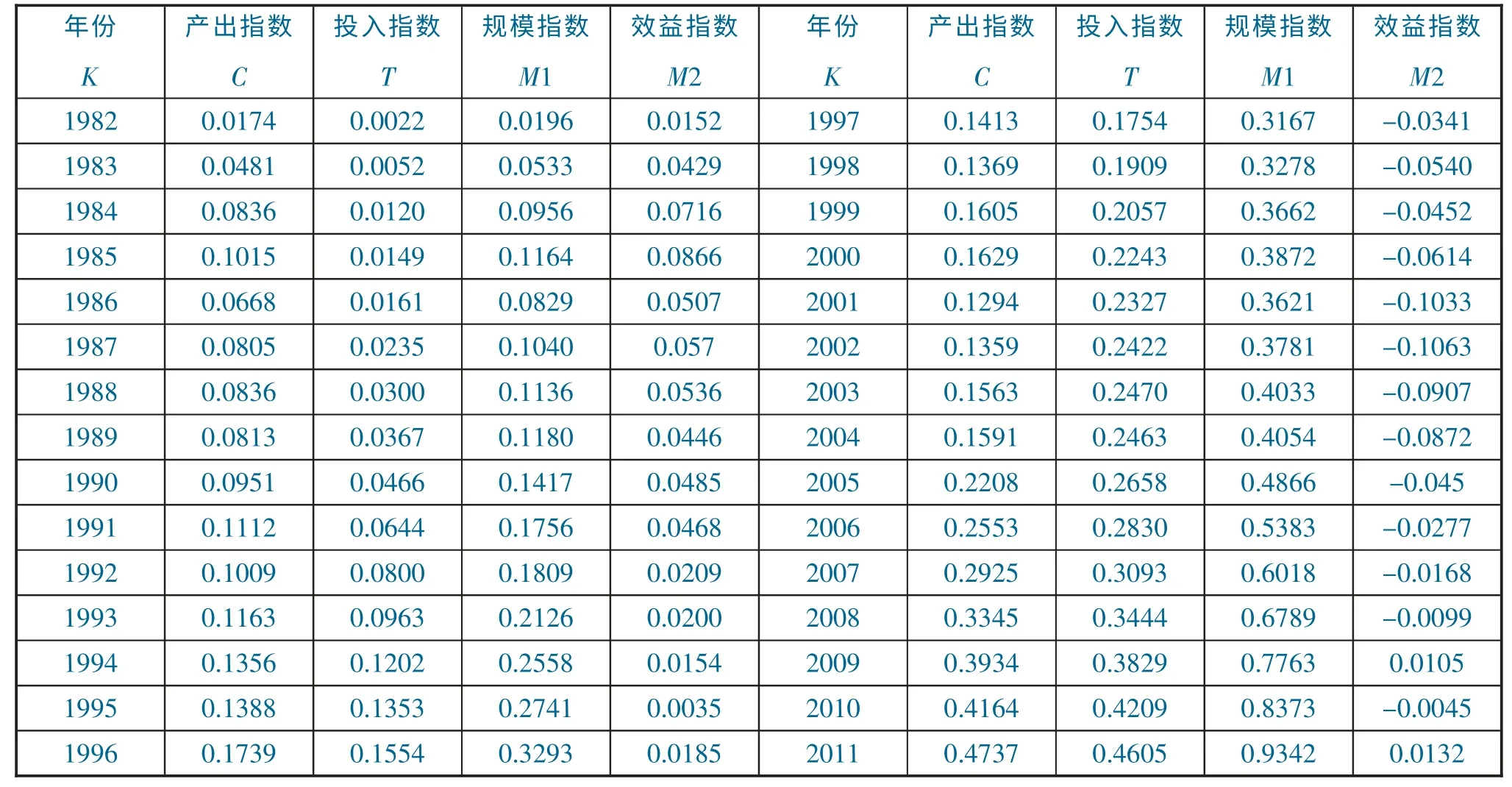
表3 1982-2011 年中国农业投入产出指数
3.农业投入产出指数的波动趋势分析
(1)波动趋势描述。为了能够更加清晰地描述近30 年来中国农业投入产出各类指数的波动趋势,可将表2 中的数据在Excel 中转换为散点图形式,见图1。
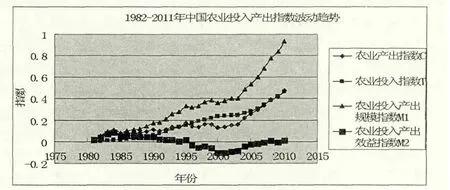
图1 1982-2011 年中国农业投入产出指数波动趋势
(2)波动趋势的回归拟合。为了能够更加准确地把握中国农业投入产出指数波动的历史轨迹与未来走势,还可以对图1 中的指数曲线进行回归分析,进而得出实际波动曲线的拟合函数曲线。本文接下来针对农业投入产出规模指数M1 和农业投入产出效益指数M2 进行回归分析。根据对图1 的观察,指数M1、M2 与年份(K)之间显然不具备线性相关的特征,进一步观察发现,指数M2 以1995 年为界呈现出两种差异明显的波动特征,因此分别针对1982-2011年的指数M1、1982-1996 年的指数M2 以及1997-2011 年的指数M2 利用Excel 中的回归分析工具进行非线性回归拟合,拟合结果见表4。

表4 1982-2011 年中国农业投入产出指数M1 和M2 波动趋势的非线性回归拟合
上述三个模型的拟合优度分别接近0.96、0.60和0.74,弃真概率均小于0.5%,因此均可被确定为可信模型。两类指数完整的拟合曲线见图2。
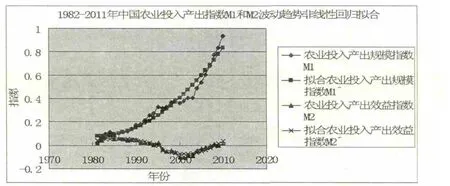
图2 1982-2011 年中国农业投入产出指数M1 和M2 波动趋势非线性回归拟合
四、测度得出的主要结论
依据前述的测度分析,本文得出的主要结论如下:
1.根据评价指标的优势分析得出的结论
(1)农业产出指标和投入指标的关联序分别表明:最能代表农业产出水平的指标是劳均农业产值,接下来依次为农民收入水平、地均粮食产量、农业出口水平和劳均粮食产量;最能代表农业投入水平的指标是农村电力投入,接下来依次为农业财政投入、农业化学投入、农业机械投入、农村水利投入、农村教育投入和农业资产投入。(2)在农业投入产出水平评价指标灰色综合关联度矩阵中:最大值ρ13=0.9429表明,劳均农业产值和农村电力投入是一组关联度最高的产出-投入关系;最小值ρ36=0.5014 表明,劳均粮食产量和农业资产投入是一组关联度最低的产出-投入关系;类似地可分析比较其他产出-投入组合的关联性大小。
2. 根据农业投入产出指数的波动趋势描述得出的结论
(1)1982-2011 年,中国的农业产出指数C、投入指数T 和规模指数M1 总体上都呈现出不断走高的态势。但是,大致以1996 年为界,此前的产出指数C高于投入指数T,说明这一阶段规模指数M1 的增长主要依靠产出拉动;此后则是投入指数T 高于产出指数C,说明这一阶段规模指数的增长主要依靠投入拉动。联系实践,改革开放之初到1990 年代中期,中国的农村改革总体上主要依靠制度创新来推动,虽然人、财、物的投入相对有限,但仍然使农业产出保持了较高的增长水平,从而带动了农业投入产出总体规模水平的提升;1990 年代中期以后,国家、集体和个人对农业的投入力度都开始加大,尤其是国家财政对“三农”的投入明显增强,使得农业产出的增幅相对较低,但总体规模的增长仍然十分显著。(2)农业投入产出的效益指数M2 的波动趋势比较复杂,总体来看先正后负且呈现“S”形波动,表明从投入产出的效益来看,中国农业投入产出水平仍存在着较为明显的阶段性特征差异。
3. 根据农业投入产出指数波动趋势的回归拟合得出的结论
(1)通过对1982-2011 年中国农业投入产出规模指数M1 波动趋势的回归拟合发现,这一时期指数M1 的运行轨迹基本吻合一段开口向上的抛物线的右半支,即指数M1 处于加速增长的态势,这基本符合近30 年来中国农业和农村发展取得显著进步和农民生活得到明显改善的事实。(2)通过对1982-1996 年中国农业投入产出效益指数M2 波动趋势的回归拟合发现,这一时期指数M2 的运行轨迹位于横坐标轴的上方,基本吻合一段开口向下的抛物线且先升后降,即指数M2 虽然为正但先减速上升后加速下滑,现实情况则是1990 年代中期以前,中国的农业发展虽然投入水平较低,但由于产出水平的起点更低,所以产出的增长幅度相对较高,但随着时间的推移,这种产出相对于投入的边际优势不断弱化,农业投入增长相对过慢已经制约了农业产出水平的提升。(3)通过对1997-2011 年中国农业投入产出效益指数M2 波动趋势的回归拟合发现,这一时期指数M2 的运行轨迹位于横坐标轴的下方,基本吻合一段开口向上的抛物线且先降后升,即指数M2 虽然为负但先减速下滑后加速上升,现实情况则是1990 年代中期以后,国家、集体和个人加大了对农业的投入,但由于短期内对农业产出的促进作用不明显,所以出现了负效益,随着时间的推移,这种产出相对于投入的边际劣势不断弱化,尤其是近年来,在农业投入力度持续增强的作用下农业产出增幅开始加速,农业投入产出效益指数M2 不仅转负为正,而且呈现加速上升的态势,未来极有可能实现农业投入产出规模水平和正向效益水平的双增长,这意味着中国的农业生产发展已先后摆脱“高效益、低水平”和“高水平、低效益”的非良性状态,开始步入“高效益、高水平”的良性发展轨道。
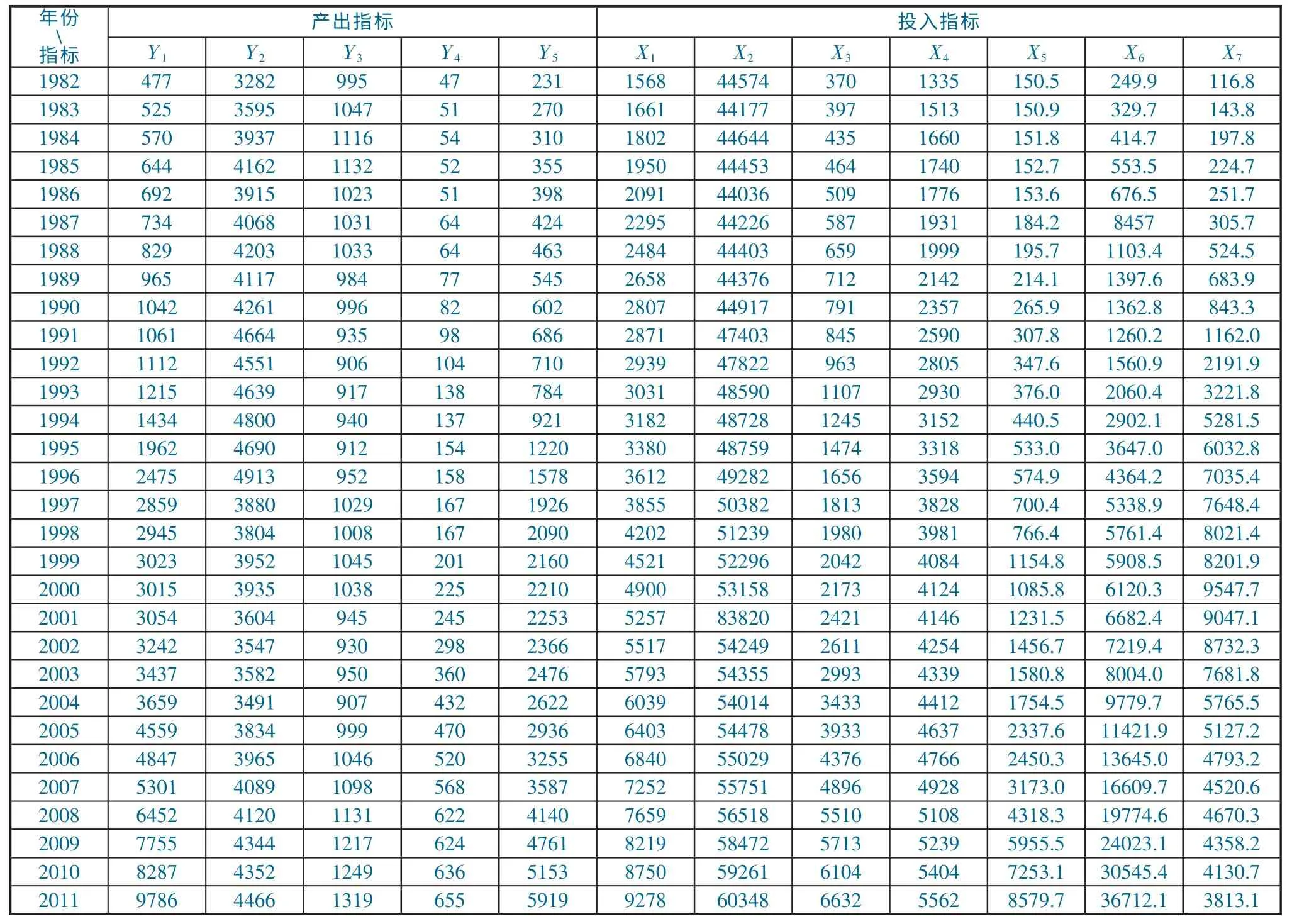
附表1 1982-2011 年中国农业投入产出水平评价指标的实际值
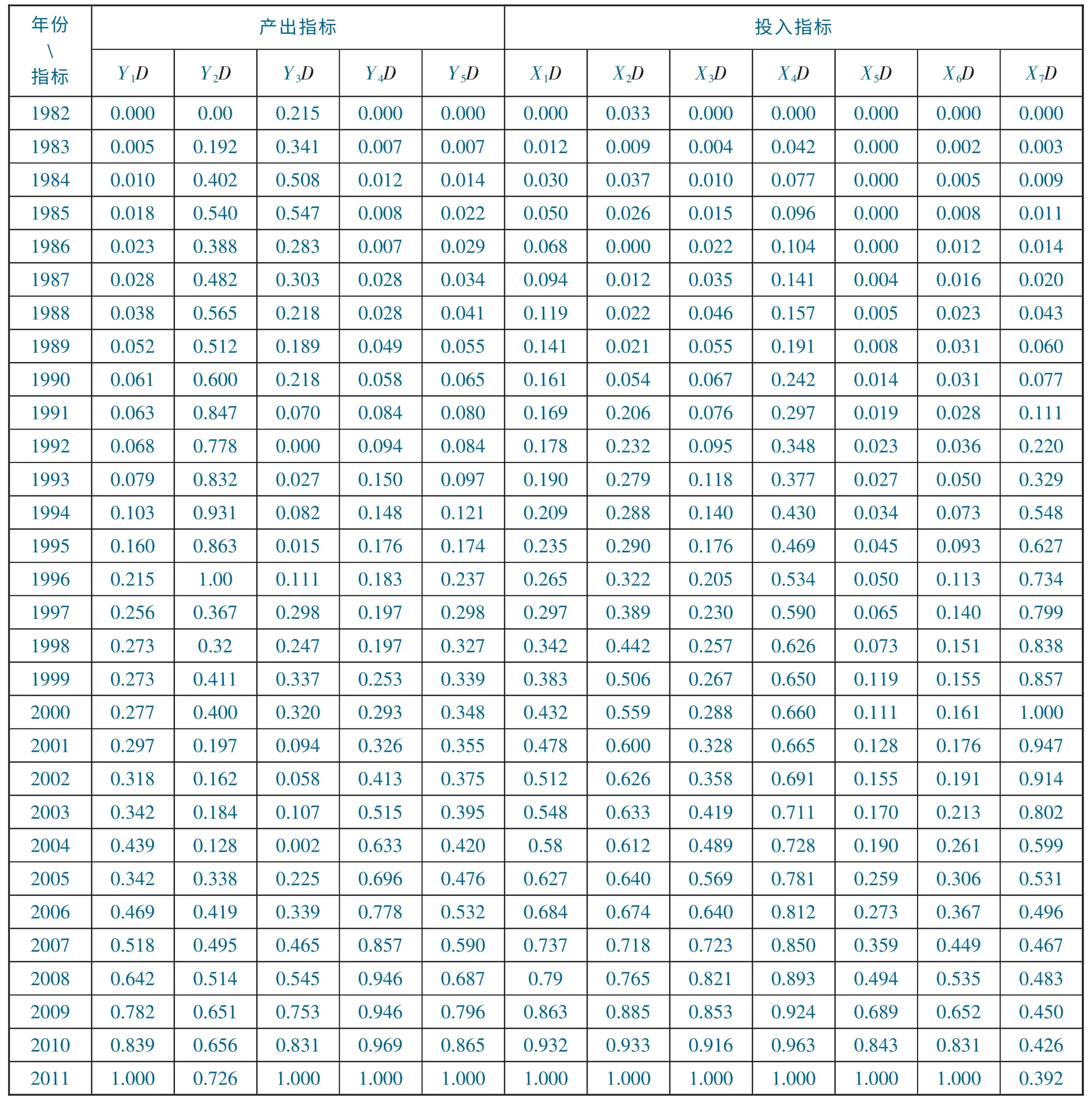
附表2 1982-2011 年中国农业投入产出水平评价指标的标准值
[1]冯子华,覃炳英.海南省农业投人产出的定量评价[J].热带作物学报,1994,(1).
[2]林玉蕊.农业投入产出生产函数及其应用研究[J].数学的实践与认识,2007,(13).
[3]张立超,瞿印礼.我国农业投入产出的关系研究[J].统计与决策,2010,(14).
[4]史明瑛,朱云鹃.安徽省农业投入产出效果分析[J].运筹与管理,1999,(2).
[5]陈健芬.我国沿海发达地区财政农业投入产出的弹性分 析[J].经 济 纵 横,2011,(3).
[6]冯启磊,王红瑞,白颖,刘琼.中国农业产出水平的影响因素分析[J].安徽师范大学学报(自然科学版),2010,(3).
[7]王学超.关于农业投入产出的回归分析模型[J].经济师,2009,(2).
[8]徐建中,王莉静,赵忠伟.基于灰色关联分析的区域主导产业选择研究[J].科技进步与对策,2010,(9).
[9]吴凯,卢布,袁璋.区域农业结构的灰色关联分析与优势产业的发展[J].中国农学通报,2006,(10).
[10]刘思峰等.灰色系统理论及其应用(第5 版)[M].北京:科学出版社,2010.
