应用DWT－FMM计算二维电大导体目标RCS

齐 琦， 陈明生， 吴先良， 刘 艺

（1.合肥师范学院 电子信息工程学院，安徽 合肥 230061；2.合肥师范学院 计算机科学与技术系，安徽 合肥 230061）

矩量法（MOM）是求解微分方程和积分方程的一种重要方法［1］，自提出后已广泛应用于计算电磁学。然而，随着电大尺寸目标的计算需求增加，MOM的诸多缺陷也被人们发现，如计算时间较长，内存占用较大等。为了克服该方法的缺陷，多种快速算法应运而生。具有代表性的有自适应积分法（AIM）［2］、共轭梯度快速傅里叶变换法（CG－FFT）［3］、快速多极子法（FMM）等［4－7］，其中FMM效果尤为显著。

MOM在电磁散射计算问题中，需将散射体表面离散成多个单元来表示电流元，通过格林函数来严格表述场单元与源单元之间的相互作用，生成一个稠密的阻抗矩阵。而FMM则采用远场近似的思想，避免阻抗矩阵的直接生成，从而节约了计算时间和内存消耗。虽然FMM在计算复杂度上有了很大的优化，但是对于较大的电大尺寸目标的计算，仍需较多的时间和内存。因此，如何进一步优化成为必要的研究课题。

离散小波变换（DWT）［8］作为一种强大的数学工具，在计算电磁学中，常应用于阻抗矩阵的稀疏化预处理。本文将该技术与FMM结合，在计算远场组作用时加入DWT，使得矩阵中的某些元素比其他元素小，并忽略它们以使解聚和聚集矩阵稀疏化，从而加速积分方程的求解；通过对不同几何形态的二维电大理想导体目标的电磁散射特性进行分析，验证了DWT－FMM 方法的正确性。

1 导体目标的矩量法解

在外加电场激励二维导体圆柱的情况中，柱体产生了感应面电流Jz，同时所有的线性电流元Jzdl又叠加产生了一个散射场，即

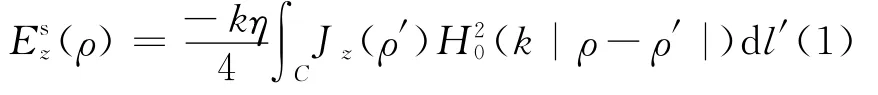
由导体表面C上电场切向分量为0的边界条件

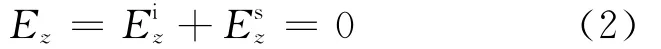
得到积分方程：

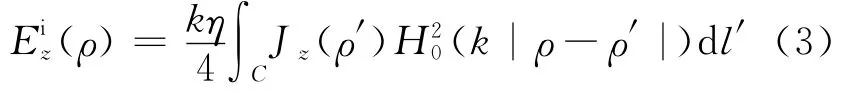
其中，（ρ）为已知的激励源；Jz为未知的感应面电流；k为波数。采用脉冲函数为基函数将积分方程离散，并以狄拉克函数作检验函数。为此，将柱体轮廓C分为N个单元ΔCn。脉冲函数的定义为：

对Jz采用脉冲基函数展开得到：

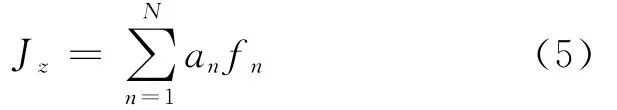
将（5）式代入（3）式，并在每个 ΔCm的中点（xm，ym）满足所得方程，便得到矩阵方程：

其中，Zmn为阻抗矩阵；an为待求的表面电流系数向量。Zmn中的元素按（7）式计算：

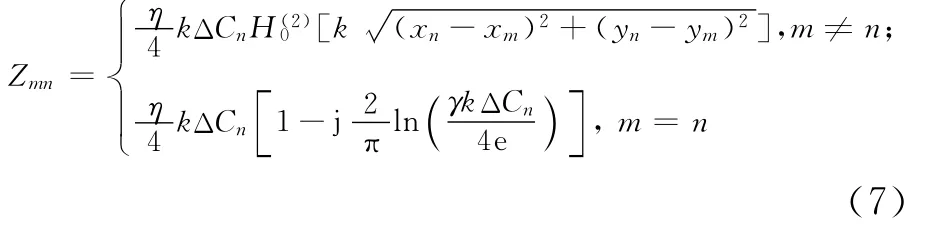
其中，ΔCn为每个单元的长度；γ＝1.781 07为欧拉常数。若阻抗矩阵是非奇异的，即Zmn－1存在，则电流系数向量可由（8）式解得：

并由（9）式求得目标的RCS，即

2 DWT技术的一般应用

在求解大型稠密的矩阵方程问题中，为了降低计算的复杂度，将矩阵稀疏化是惯用的思路。DWT是一种有效的稀疏化方法，在计算电磁学中，常用于MOM的阻抗矩阵预处理技术。以（6）式为例进行小波变换得：

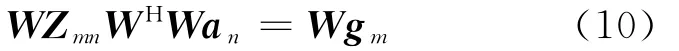
其中，W是小波变换矩阵，为正交阵；WH表示W的共轭转置；WWH＝I，I为单位矩阵。经（10）式处理后可以得到：

由于小波变换的性质，在变换后的阻抗矩阵中，有很大一部分元素与另一部分相比，会显得很小。这些很小的元素是矩阵中的高频分量，包含的信息量很小。若此时设定一个合适的阈值，将小于阈值的矩阵元素全部置0，阻抗矩阵便得到了稀疏。在得到矩阵方程（11）式的解后，对其作小波逆变换an＝WH，便得到了原方程（6）式的近似解。

W的构造过程如下：

小波滤波器具有α阶消失矩，其系数为h（k），k＝0，1，2，…，2α－1，k取其他值时，h（k）＝0，滤波器宽度为m＝2α。

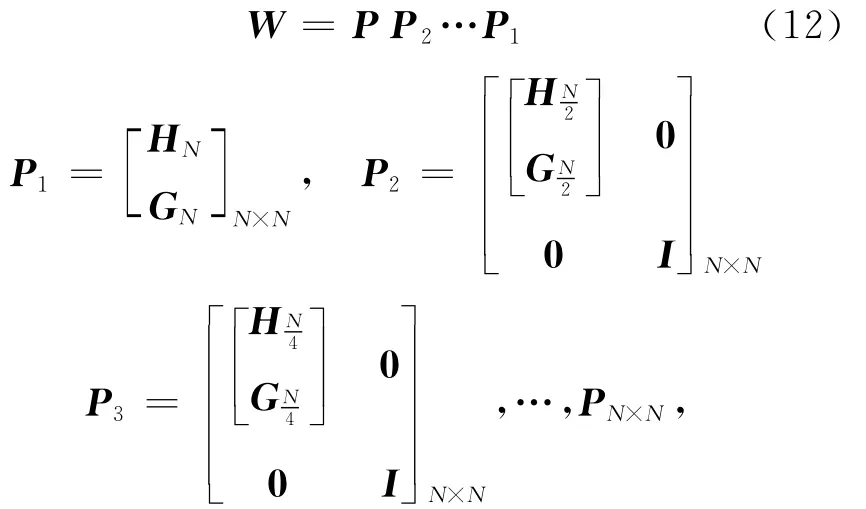
其中，HN、GN是（N／2）×N的矩阵，分别由长度为N的向量［h（2α－1），…，h（2），h（1），h（0），0，…，0］和［－h（0），h（1），－h（2），…，（－1）j＋1h（j），…，h（2α－1），0，…，0］以2为周长圆周移位得到，由其结构可知，W是一个非常稀疏的矩阵，且随着N的增大，其稀疏化程度会越来越高。

3 DWT－FMM

在外加电场Eiz激励二维理想导体圆柱的情况中，传统FMM将柱体轮廓上的N个单元分成G组，每组包含M个单元，即N＝GM。对于任意一组，其余的组可以分为近场组和远场组2类。通常定义2组的中心点距离小于半个波长的为近场组，否则为远场组。在一般的二维电大目标情况中，定义每组相邻的左右2组为其近场组，如图1所示。

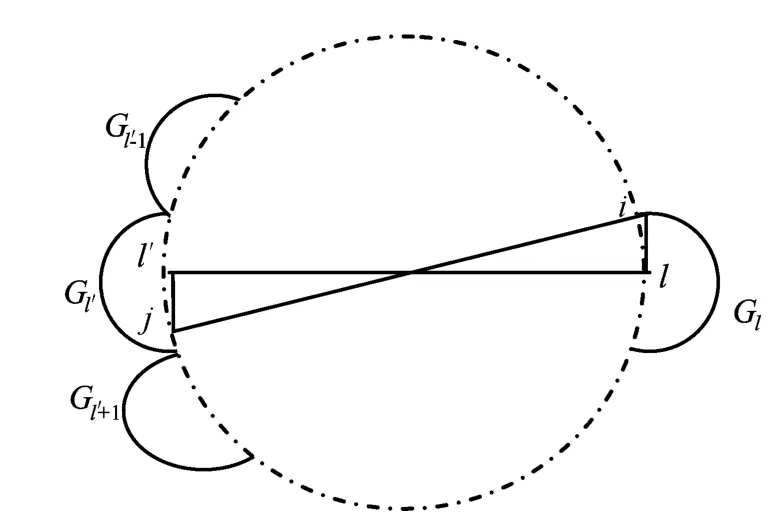
图1 远场组示意图

FMM利用远场近似思想避免稠密阻抗矩阵的直接生成，将远场作用过程分解成聚集、转移、发散3个步骤：① 聚集是将Gl内M个单元所对应的等效电流聚集在组的中心位置，其目的是为了获得具有转移特性的新函数组，即Gl内所有等效电流对远场组的作用能够由通过转移这组新函数完成；②转移是将聚集所得到的一组函数由Gl的中心位置转移到Gl′的中心位置；③ 发散是将转移到Gl′中心位置的那组函数发散到组内的所有M个单元对应的等效电流上，从而计算出Gl和Gl′的远场相互作用。任意组Gl′的单元j受到其所有远场组Gl内任意单元i作用的总和Fbj按（13）式计算：

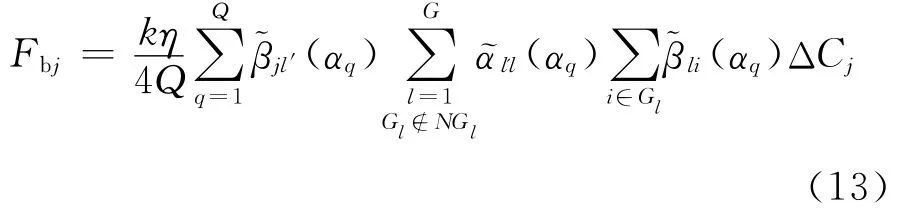
其中

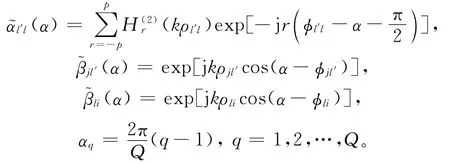
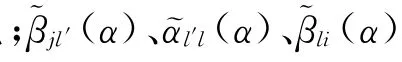
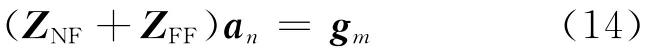
本文所提出的DWT－FMM技术是对传统FMM中解聚和发散2个步骤进行优化。在每组中，总是存在一些与中心点作用比较小的单元，在发散和解聚的计算过程中忽略这些弱作用单元仍能得到较为满意的结果。由上述可知，组Gl与Gl′的远场作用矩阵由（15）式得到：

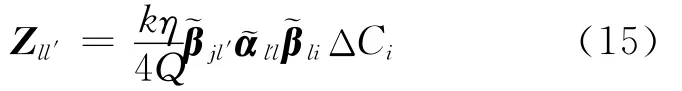
对（15）式中的解聚和发散矩阵做单边DWT，则有：

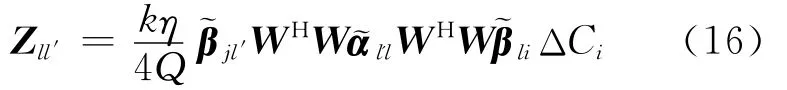
若在（16）式中令：

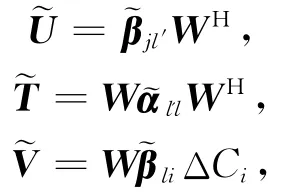
则（16）式变化为：

将和中小于给定阈值的元素置0，从而矩阵得到了稀疏。

4 数值仿真结果

为了验证该方法的有效性，本文分别对理想导体圆柱和方柱的RCS特性进行计算。将频率为300MHz的TM波垂直入射到半径为10m的无限长电大理想导体圆柱和边长为20m的无限长电大理想导体方柱上。文中定义矩阵的压缩率是矩阵中现有非零元素的个数与压缩前非零元素个数的比值。DWT－FMM方法有着较为可观的压缩率，见表1所列。

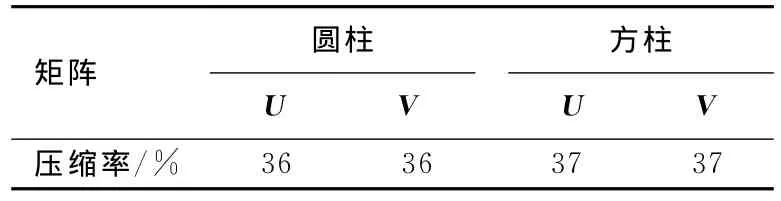
表1 矩阵压缩率

以圆柱中任意一组的解聚矩阵来查看其压缩前后的情况，如图2所示，黑色部分代表非零元素，可以看出，压缩后的矩阵中非零元素只占了很小的比例。

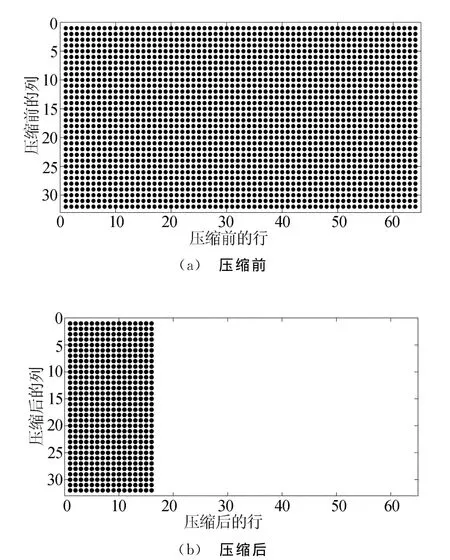
图2 解聚矩阵

将2种方法所得到的目标RCS进行对比，如图3、图4所示。显然，DWT－FMM的精确性是优秀的。

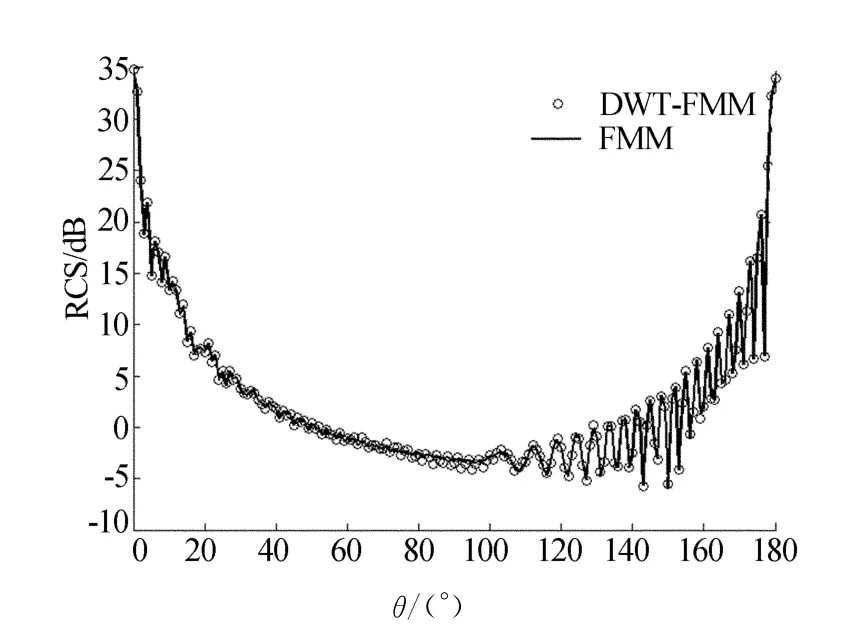
图3 方柱RCS

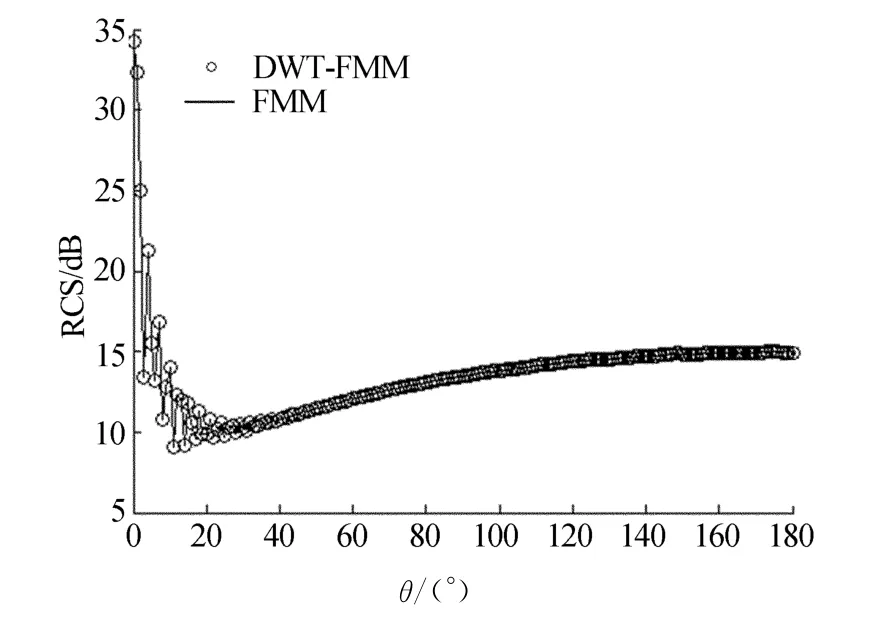
图4 圆柱RCS

5 结束语

本文应用小波变换的特性使得快速多极子中的解聚和聚集矩阵得到了充分的稀疏，提高了传统快速多极子的效率。计算结果表明，DWTFMM方法在计算电大导体目标电磁散射特性时，有效降低了计算复杂度，对电脑内存的消耗有着可观的改善。

［1］ Harrington R F.Field computation by moment methods［M］.New York：IEEE Press，1993：65－687.

［2］ Bleszynski E，Bleszynski M，Jaroszewicz T.AIM：adaptive integral method for solving large－scale electromagnetic scattering and radiation problems［J］.Radio Science（S0048－6604），1996，31（5）：1225－1251.

［3］ 谢处方，吴先良.电磁散射理论与计算［M］.合肥：安徽大学出版社，2002：1－144.

［4］ Of G，Steinbach O，Wendland W L.The fast multipole method for the symmetric boundary integral formulation［J］.IMA Journal of Numerical Analysis，2006，26（2）：272－296.

［5］ Engheta N，Murphy W D，Rokhlin V，et al.The fast multipole method（FMM）for electromagnetic scattering problems［J］.IEEE Transaction on Antennas and Propagation，1992，40（6）：634－641.

［6］ Coifman R，Rokhlin V，Wandzuraz S.The fast multipole method for the wave equation ［J］.IEEE Antennas and Propagation Magazine，1993，35（3）：1－12.

［7］ 盛新庆.计算电磁学要论［M］.合肥：中国科学技术大学出版社，2008：1－194.

［8］ 陈明生，孙玉发，沙 威，等.应用DWT－DWT方法快速计算二维电大介质目标 RCS［J］.电波科学学报，2002，21（2）：220－224.