欠驱动移动机器人的路径跟踪控制

杨兴明， 朱 建， 高银平， 许东昌

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

0 引 言

轮式移动机器人是一种典型的具有非完整约束的系统，因其具有广泛的应用前景和理论意义引起了国内外学者的广泛关注［1－6］。近年来，根据基于的模型不同，移动机器人路径跟踪的研究可以分为基于运动学模型和动力学模型2种研究方式。基于运动学模型的研究主要是以速度作为控制量使真实轨迹和参考轨迹之间的误差收敛到0，研究的是速度和参考轨迹之间的关系。基于动力学模型控制器反映的是控制电压和速度之间的关系，能够比较真实地反应移动机器人的控制规律。

文献［7－8］基于动力学模型，利用自适应的方法实现了三轮移动机器人的路径跟踪。考虑到双轮移动机器人比三轮或四轮机器人具有更好的机动性和灵活性，体积更小，尤其是在拥挤的空间，更能体现其灵活性，双轮移动机器人的路径跟踪也同样具有很高的研究价值。

本文针对双轮移动机器人的研究首先建立系统的运动学模型和动力学模型，并针对运动学模型通过反演技术设计运动学控制器，进而考虑到系统的不确定性和跟踪速度与姿态平衡控制欠驱动的特点，基于动力学模型设计了分层滑模控制器，最后通过Matlab仿真验证该控制方法的有效性。

1 双轮移动机器人模型的建立

（1）双轮移动机器人的运动学模型。在机器人移动的区域内建立笛卡尔坐标系（Oxy），选择移动机器人2个驱动轮轴线的中点坐标（xc，yc）作为参考点，则机器人的位姿可以描述为：p＝［xc，yc，θ］T，其中θ为机器人的方向角。假设机器人运动满足纯滚动无滑动的约束条件，则根据文献［9］可以得到系统的运动学方程：

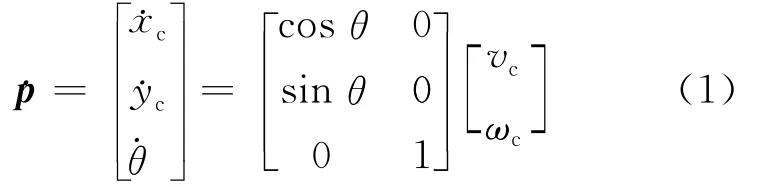
其中，vc、ωc分别为小车运动速度和转弯角速度。

（2）双轮移动机器人的动力学模型。图1所示为双轮平衡机器人的简化模型。其中，R表示车轮半径；l表示车体重心到电机轴线之间的距离；D表示两轮之间的距离。

下文中用到的符号含义如下：x、v表示车底盘中心的位移和速度；δ表示摆杆与竖直方向的角度；θ、ω表示车体绕竖直方向旋转的角度和角速度；Mp、mr分别表示车体质量和小轮的质量；Jr、Jp、Jθ分别表示小轮绕轴的转动惯量、车体绕电机轴的转动惯量和车体绕摆杆的转动惯量；φ表示斜坡角度，在这里取0；；Km、Ke表示电机的力矩系数和电机的反电动势系数；ul、ur表示左右轮的控制电压；cl、cr表示左右电机的输出转矩。

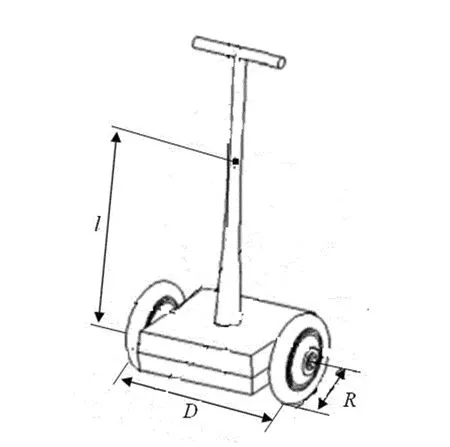
图1 双轮移动机器人的简化模型

［10］，利用牛顿力学的建模方法对系统建模，可以得到与系统状态相关的方程组，即

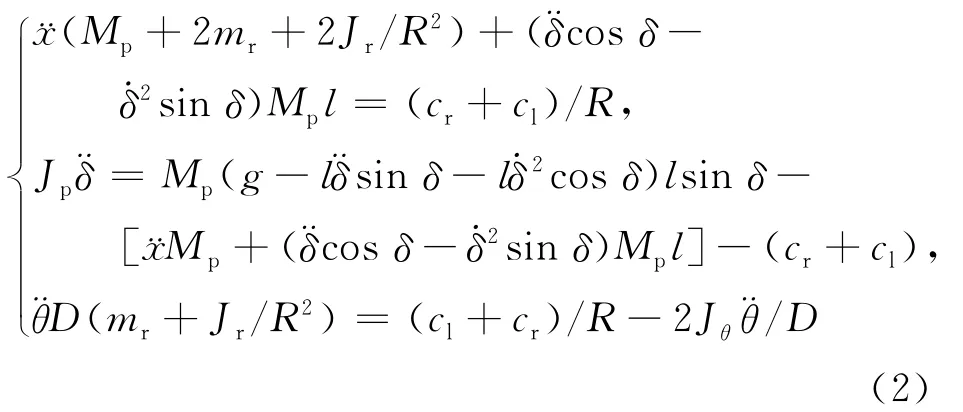
定义X＝［δ，x，，v，θ，ω］T为状态变量，对（2）式进行线性化后，利用电机的输出转矩和控制电压的关系c＝Km（u－K），把状态方程中控制量cl、cr转化为由电机的输入电压ul、ur作为控制量。然后定义ul＝0.5uv＋0.5uω，ur＝0.5uv－0.5uω，可以得到系统的状态方程为：

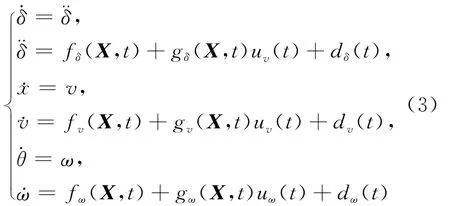
其中

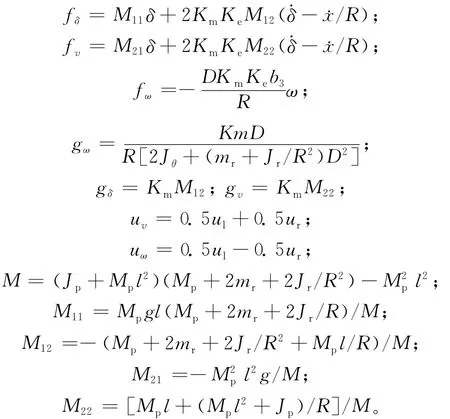
其中，uv（t）、uω（t）为控制输入；fv（X，t）、fδ（X，t）、fω（X，t）不确 定 部 分 分 别 为 Δfv（X，t）、Δfδ（X，t）、Δfω（X，t），假设系统不确定部分上界已知，且满足｜Δfv（X，t）｜≤ΔFv，｜Δfδ（X，t）｜≤ΔFδ，｜Δfω（X，t）｜≤ΔFω；dv（t）、dδ（t）、dω（t）为界干扰且满足条件｜dv（t）｜≤Dv，｜dδ（t）｜≤Dδ，｜dω（t）｜≤Dω。

由于系统的平衡角度难以大范围可控，因此必须对系统平衡角度的控制范围进行分析，系统平衡角度的临界值可以定义为δ0，当δ的变化超过δ0时，即使电机对系统施加最大的力矩，也不能使系统回到平衡点附近。当｜δ｜＝δ0时，机器人平衡角度的变化速率＝0，假设机器人两轮的运动速度是相同的，则可以得到系统的综合边界条件为：

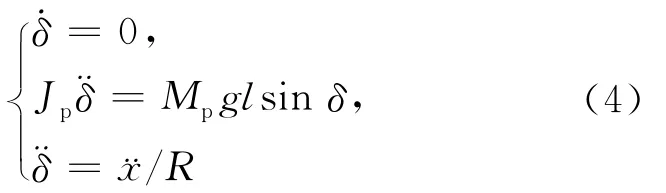
把（4）式代入（2）式中前2个式中的任意一个，例如代入第1个式中并假设两电机的最大扭转力矩相同为Cm，可得：

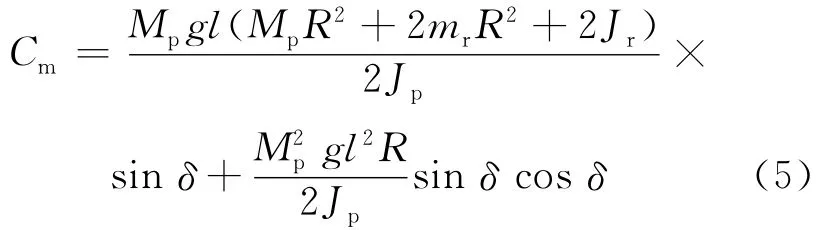
将各参数值代入（5）式并由电机的最大扭转力矩Cm＝6.8N·m，可以求得系统平衡角度的控制范围为：－27.6°≤δ≤27.6°。

2 双轮移动机器人控制器的设计

图2所示为双轮机器人的系统结构图，其中，pd＝［xd，yd，θd］T表示参考位姿；ep＝［ex，ey，eθ］T表示跟踪误差；Vc＝［vc，ωc］T为运动学控制器输出的控制速度和角速度；e＝［ev，eω］T表示动力学控制器对Vc的跟踪误差；eδ为机器人平衡角度δ的跟踪误差，在机器人的运动过程中希望其能够保持竖直，所以取δd＝0；u＝［uv，uω］T表示动力学控制器的输出电压，由于机器人的欠驱动特点uv控制机器人的速度v和平衡角度的变化速率，uω控制机器人的转弯角速度ω；V＝［v，ω］T表示机器人的实际速度和转动角速度；p＝［xc，yc，θ］T表示机器人的实际位姿。

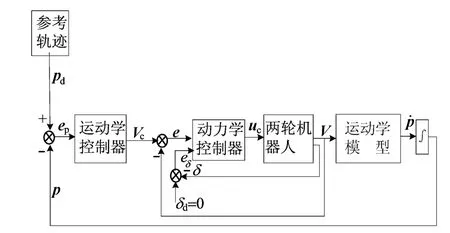
图2 双轮移动机器人系统结构图

2.1 运动学控制器的设计

在固定的坐标系内系统的位姿误差为：

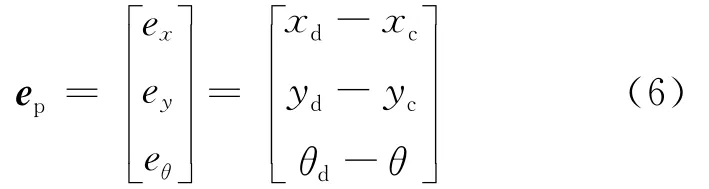
通过反演法设计控制器，步骤如下。

（1）引入虚拟量α。根据（1）式有：

构造Lyapunov函数：

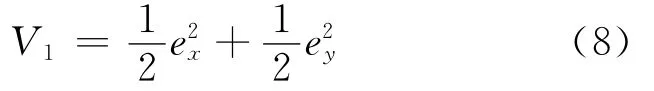
对V1求导，并把（7）式代入可得：

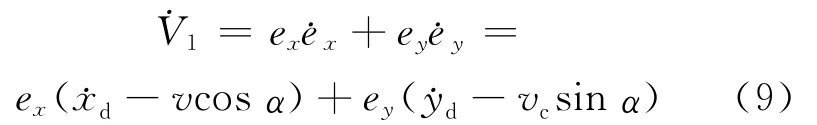
则需设计虚拟量α满足如下条件：

其中，C1＞0；C2＞0。则由（10）式可得线速度vc和虚拟控制量α为：

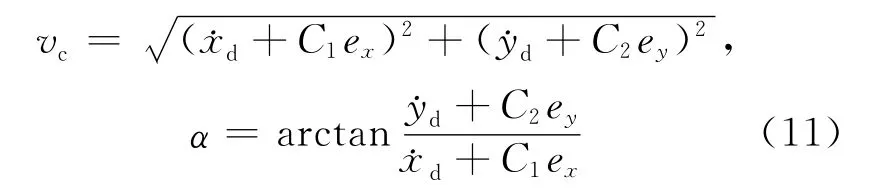
（2）定义z＝α－θ，实现θ跟踪α。构造Lyapunov函数为：

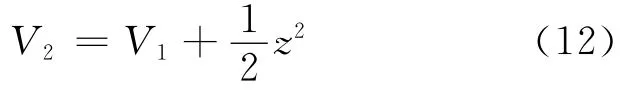
对（12）式求导：

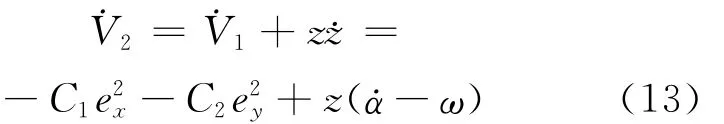
取角速度ωc的控制率为：

则有：

2.2 动力学控制器的设计

双轮移动机器人的动力学系统可以分为平衡控制系统、速度控制系统和转弯角速度控制系统3个子系统，由于其平衡控制子系统和速度控制子系统由同一个控制电压uv来控制，所以具有欠驱动的特点，为了避免复杂的解耦过程，本文采用分层滑模控制器控制机器人的平衡角度δ和运动速度v，采用传统的滑模控制器控制机器人的转弯角速度。

定义ev＝vc－v，eω＝ω－ωc，eδ＝－δ，设计第1层滑模面为：

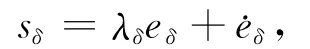
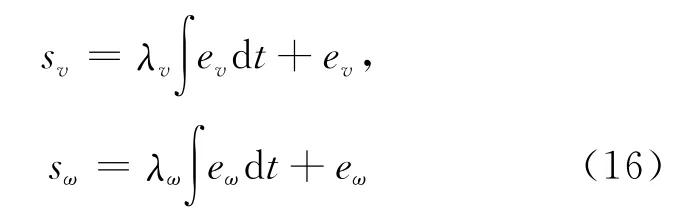
其中，λδ、λv、λω为待设计正的滑模面常系数。

对（16）式求导，并结合（3）式可以得到：

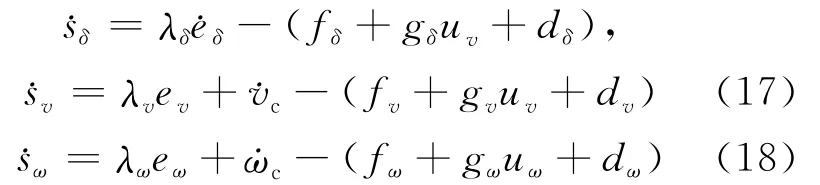
为了使得平衡控制子系统和速度控制子系统趋近各自的滑模面，令δ＝0，v＝0，先不考虑dδ、dv对系统的影响，则每个子系统的等效控制律可以取为：

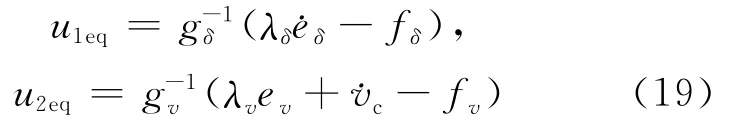
为了使得平衡角度δ和运动速度v跟踪误差都为0，则根据第1层滑模面（16）式定义第2层滑模面：

其中，λ为正常数。取趋近率：

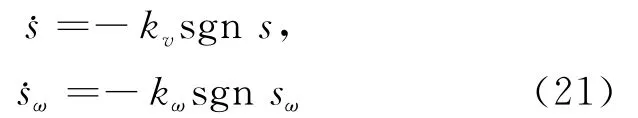
结合（18）式、（19）式可设计系统的控制律为：

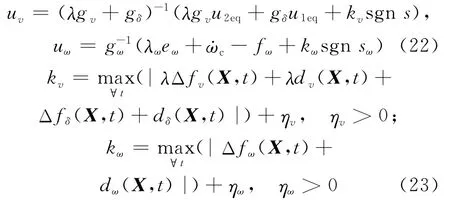
其中，kv、kω为切换项增益，为正常数。增加系统的切换项主要是为了提高控制器的抗干扰能力。

为了证明系统的稳定性，在系统的可控范围内，构造Lyapunov函数：

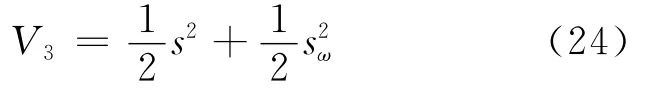
则对V3求导，然后结合（17）～（19）式和（22）式可得：

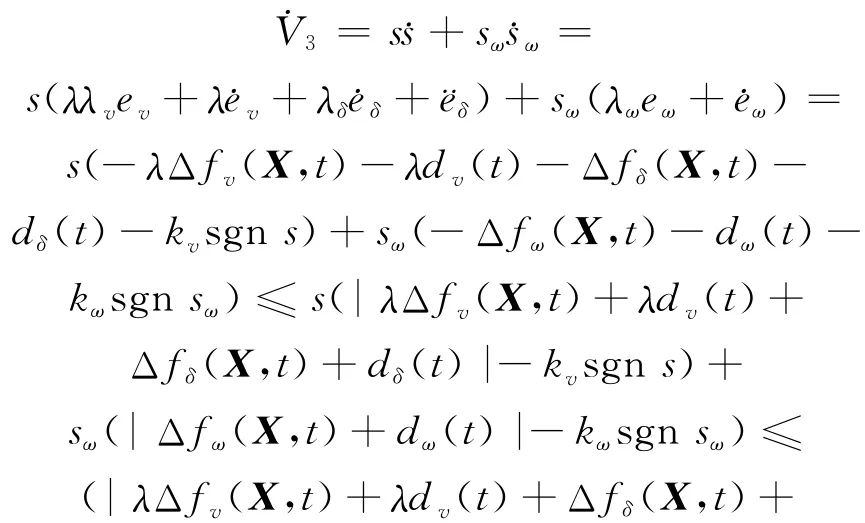
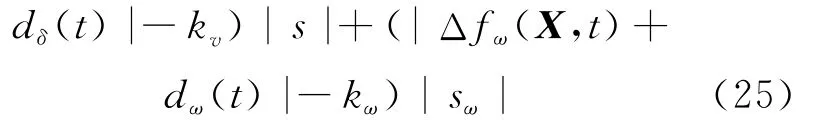
由（23）式可知：

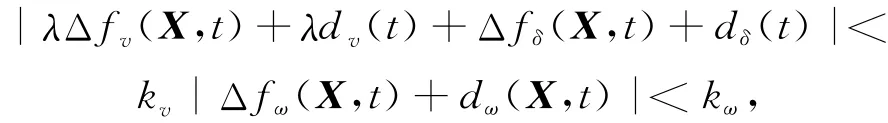
所以＜0，则系统的滑动模态存在且可达，系统稳定。

为了抑制传统滑模控制器由于控制率的不连续性导致的抖振问题，在滑模面附近引入边界层，用脉冲函数取代不连续的符号函数。此时控制律为：

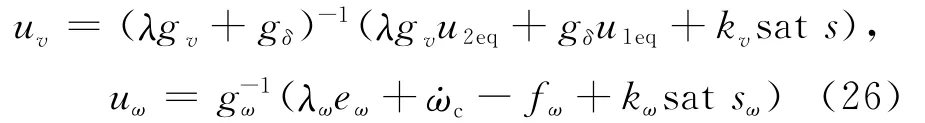
脉冲函数sat（·）被定义为：

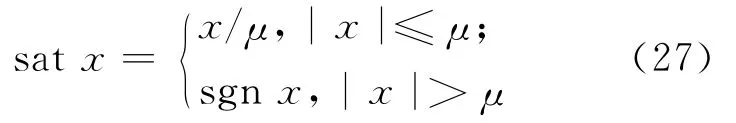
其中，μ为边界层宽度。

3 仿真结果

3.1 仿真参数的选取

通过简化模型转换为状态方程：

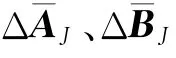
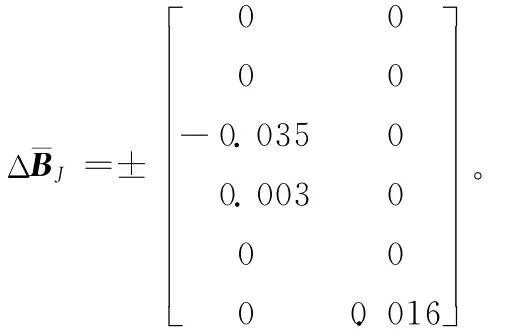
外界的干扰主要由路面的不平整引起，当地面的坡度为5°，造成的干扰为dθ＝1.377 1，dx＝－0.903 8。

（2）控制器中的参数取值。λv、λδ、λω、λ的选择决定了滑模面的性能特征，本文参考文献［11］采用零极点配置的方法选取λω＝1.520，λδ＝3.975 3，λv＝0.862 3，λ＝1.744。其他参数：kω＝6，μ＝10，kv＝15，C1＝0.5，C2＝0.5，C3＝2。

3.2 仿真结果及分析

为了验证本文所提出算法的有效性，在加入系统不确定性干扰的条件下，利用本文设计的控制器对双轮机器人进行轨迹跟踪控制仿真。

（1）直线轨迹的跟踪。假设给定的参考轨迹是一条起始点为（0，0）、斜率为π／4的直线。机器人的初始位姿为（0.2，0，π／3），初始姿态角度为8.6°，在t＝20s时引入5°坡造成的脉冲干扰dθ、dx。在0～30s的时间内对参考曲线以0.1m／s的速度进行跟踪仿真，结果如图3～图6所示。

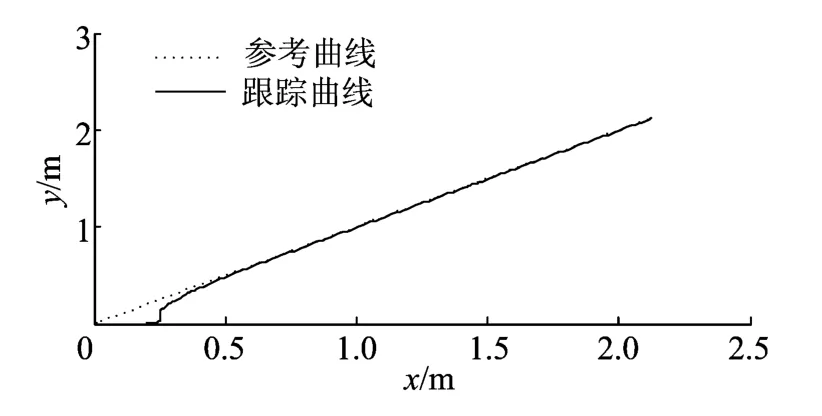
图3 0～30s内移动机器人平面运动曲线

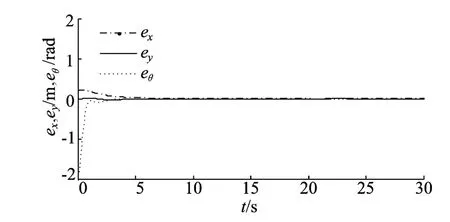
图4 0～30s移动机器人的位姿误差

从图4的位姿误差曲线可以看出，移动机器人在6s内跟踪误差收敛到0，对直线具有良好的跟踪性能，在20s时引入外界干扰，系统仍可以稳定跟踪参考曲线。

2008年后，随着中国地质调查局新一轮区域化探项目的实施[1]，青海省第五地质矿产勘查院承担并完成了青海柴达木盆地周缘的区域化探扫面工作，并在该区新圈定了一大批面积大、强度高、具有找矿前景的化探异常[2]，通过对少数地球化学异常检查，新发现夏日哈木等矿(床)点数十处[3]，极大的推动了该区的地质找矿工作。但该景观区的化探方法技术研究工作较少[4-6]，这使得人们对该区的化探采样工作更加关注。

从图5的仿真曲线可以看出，移动机器人自身在4s内达到平衡，在5s内速度达到并保持在0.1m／s。

综上所述，本文设计的控制方法可以在保持双轮移动机器人自身平衡的同时稳定地跟踪期望的直线轨迹。

（2）圆轨迹的跟踪。假设给定的参考轨迹的圆方程为：x2＋y2＝1，其起始点为（1，0），机器人的初始位姿为（0.8，0，0），初始姿态角度δ为8.6°，在t＝40s时引入5°坡造成的脉冲干扰dθ、dx。在0～70s的时间内对参考曲线以0.1m／s的速度进行跟踪仿真，结果如图7～图10所示。

从图8的位姿误差曲线可以看出，移动机器人在8s内跟踪误差收敛到0，在20s时引入外界干扰，系统仍可以稳定跟踪参考曲线，说明系统对圆具有良好的跟踪性能。

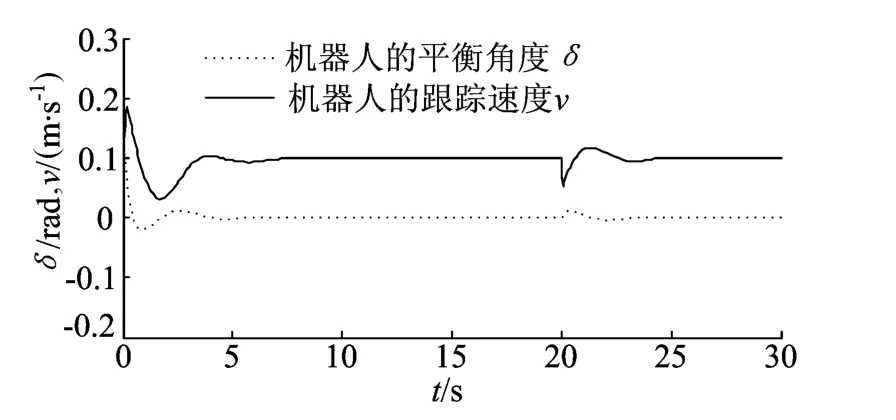
图5 0～30s机器人的平衡角度和速度

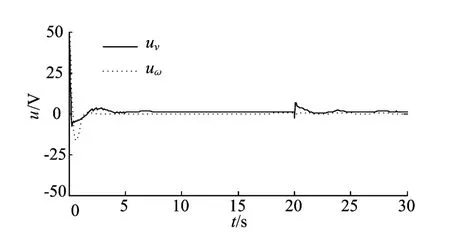
图6 0～30s控制电压

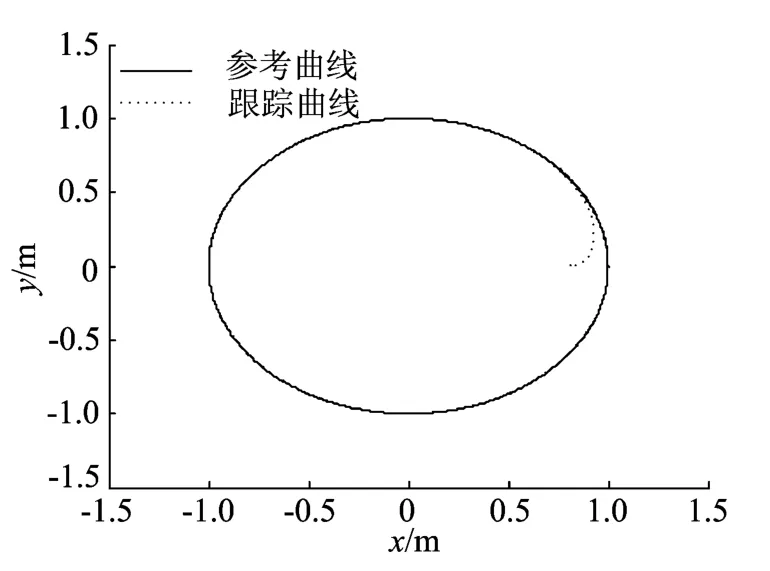
图7 0～70s移动机器人平面运动曲线

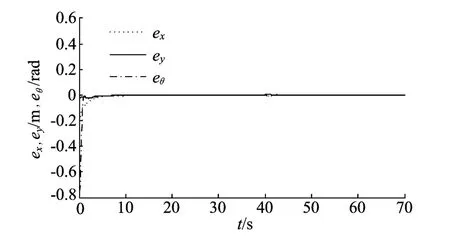
图8 0～70s移动机器人的位姿误差

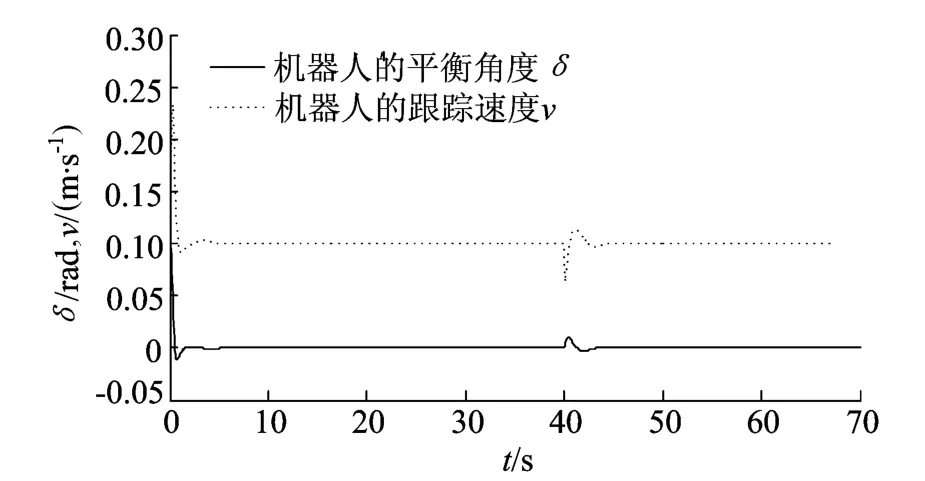
图9 0～70s机器人的平衡角度和速度

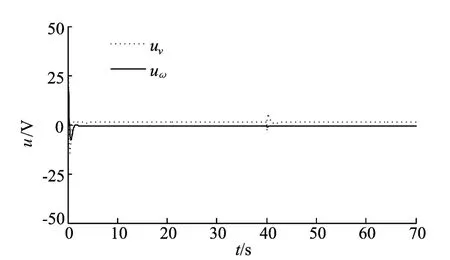
图10 0～70s控制电压

从图9的仿真曲线可以看出，移动机器人在5.5s内达到姿态平衡，在7.5s内速度达到0.1m／s。

综上所述，本文设计的控制方法可以在保持双轮移动机器人自身平衡的同时稳定地跟踪期望的圆轨迹。

4 结束语

本文针对双轮机器人的路径跟踪问题，把系统的控制分为运动学控制和动力学控制2个部分。在动力学控制中，由于系统的姿态平衡和跟踪速度的欠驱动特点，本文采用分层滑模控制器实现对跟踪速度和姿态平衡的控制。在加入系统不确定性干扰的条件下，对直线轨迹和圆轨迹的跟踪控制进行仿真，仿真结果表明该控制方法可以控制双轮移动机器人在保持姿态平衡的同时实现轨迹的精确跟踪。

［参考文献］

［1］ Morin P，Samson C.Control of nonholonomic mobile robots based on the transverse function approach［J］.Robot，2009，25：1058－1073.

［2］ Fukao T，Nakagawa H，Adachi N.Adaptive tracking control of a nonholonomic mobile robot［J］.Robot，2000，16：609－615.

［3］ 郁 伉，肖本贤，李艳红.受非完整性约束的移动机器人路径跟踪算法［J］.合肥工业大学学报：自然科学版，2010，33（9）：1315－1319.

［4］ 杨 芳，王朝立.不确定非完整移动机器人的轨迹跟踪控制［J］.控制工程，2012，19（2）：258－261.

［5］ Buccieri D，Perritaz D，Mullhaupt P，et al.Velocity－scheduling control for a unicycle mobile robot：theory and experiments［J］.Robot，2009，25：451－458.

［6］ Coelho P，Nunes U.Path－following control of mobile robots in presence of uncertainties［J］.Robot，2005，21：252－261.

［7］ Fukao T，Nakagawa H，Adachi N.Adaptive tracking control of a nonholonomic mobile robot［J］.Robotics and Automation，2000，16（5）：609－615.

［8］ Pourboghrat F，Karlsson M P.Adaptive control of dynamic mobile robot with nonholonomic constraints［J］.Computers and Electrical Engineering，2002，28：241－253.

［9］ Jiang Z P，Nijmeijer H.Tracking control of mobile robots：a case study in backstepping［J］.Automatica，1997，33（7）：1393－1399.

［10］ 陈 星，魏衡华，张玉斌.两轮行走倒立摆系统的建模与鲁棒方差控制［J］.计算机仿真，2006，23（3）：263－266.

［11］ Ackermann J，Utkin V.Sliding mode control design based on Ackermann's formula［J］.IEEE Transactions on Automatic Control，1998，43（2）：234－237.