小波阈值去噪在传感器性能试验数据处理中的应用

田 丰，孙 剑，邵 山

（1.沈阳航空航天大学自动化学院，辽宁 沈阳 110136;2.沈阳飞机设计研究所，辽宁 沈阳 110136）

0 引言

在性能试验测试工程中，由于内部和外部噪声的干扰，总是影响后续的分析效果。因此，在对测量数据进行分析之前，能否有效地去除这些噪声干扰，以提高数据信噪比，就显得十分重要。

小波分析克服了传统傅里叶变换在单分辨率上的缺陷，具有多分辨率分析的特点，在时域和频域都有表征信号局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整。小波分析可以探测信号中的瞬态成分，并展示其频率成分，被称为数学显微镜，广泛应用于各种时频分析领域［1］。

针对航电试验信号的特点，有针对地正确选择小波函数，阈值和分解层数等参数对于处理结果起着决定性作用［2，3］。本文以传感器性能测试试验中的死区测试为例来说明这些参数的选取过程。

1 小波阈值去噪原理

假设一个含噪声的一维信号的模型可表示为

其中，e（n）为噪声，σ为噪声强度，f（n）为真实信号，s（n）为含噪信号。最简单的情况下可以假设e（n）为高斯白噪声，且σ=1［4，5］。在实际工程中，有用信号通常表现为低频信号或较平稳的信号，而噪声信号则通常表现为高频信号。所以，小波去噪的过程可细分为如下几段:

1）分解过程:选取合适的小波基函数，确定合理的分解层数，对含噪信号进行小波分解，获取各个尺度上的小波分解系数;

2）作用阈值过程:通过估计各个尺度上的高频系数的噪声水平确定阈值，然后利用该阈值对小波系数进行削减;

3）重建过程:将处理后的小波系数进行逆变换，重构得到去噪后信号。

从以上小波去噪过程可以看出:小波阈值作用函数和小波基的选择是小波去噪的关键，直接影响试验数据的去噪效果。

2 小波阈值去噪

2.1 小波阈值函数的选取

在对小波分解系数作用门限阈值处理操作时，主要有2种函数方法，硬阈值函数和软阈值函数。硬阈值处理令较小的小波系数为0，并保留较大的小波系数

软阈值处理将较小的小波系数置0，并对较大的小波系数向0作了收缩

对直线作用硬阈值和软阈值的结果见图1，从图中可以看出:软阈值处理可以有效地避免间断，使得重建的信号比较光滑，而硬阈值处理会在某些点产生间断。软阈值处理实质上是对小波分解系数作了收缩，从而Donoho-Johnstone将这种去噪技术称之为小波收缩（wavelet shrinkage）［5］。用软阈值的方法去噪能够使估计信号实现最大均方误差最小化，即去噪后的估计信号时原始信号的最优估计，所以，本文使用软阈值处理方法。

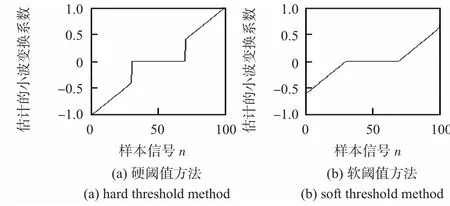
图1 硬阈值方法和软阈值方法Fig 1 Hard threshold and soft threshold method

2.2 小波阈值的确定

小波变换中，对各层系数降噪所需的阈值一般是根据原信号的信噪比来取的。在理论模型里这个量用式（1）中的t=来表示，从s（n）中提取σ的方法有很多，这里介绍4种基于样本估计的阈值函数形式［1］:

1）无偏似然估计（rigrsure）:基于Stein无偏似然估计（SURE）的软阈值估计。对于给定的阈值t，得到它的似然估计，然后将似然估计最小化，得到所需的阈值。

2）固定阈值（sqtwolog）:固定阈值t的计算公式为t=2logn，其中，n为信号的长度。

3）启发式阈值（heursure）:前2种形式的综合形式，当信噪比很小时rigrsure形式产生的阈值抑制噪声的效果不明显，这时heursure采用固定阈值sqtwolog。

4）最小极大方差阈值（minimaxi）:使得选取的阈值产生最小的极大方差。在统计学上，降噪后的信号可以看成与未知回归函数的估计式相似，所以，这种方法通过求得未知回归函数与原信号方差在最坏情况下的最小值来获取阈值。

以db5小波作为小波基，采用软阈值方法，将上述4种阈值形式分别在2～7层上进行去噪处理得到的信噪比、均方差和平滑度做对比［6］。如图2～图4所示，信噪比总是随着分解层数的增加而减少，均方差总是随着分解层数的增加而增加，然而4种阈值情况下的这2项指标并无明显的差别，反而在平滑度上固定阈值（sqtwolog）和启发式阈值（heursure）有着更好的表现，在去噪作用原理上启发式阈值（heursure）更为优秀，故选择启发式阈值（heursure）规则作用于航电伺服系统死区测试数据去噪。

图2 不同分解层数下的不同阈值规则去噪的信噪比Fig 2 Signal-to-noise ratio of de-noising of different decomposition levels different threshold rules

图3 不同分解层数下的不同阈值规则去噪的均方差Fig 3 Mean square error of de-noising of different decomposition levels different threshold rules

图4 不同分解层数下的不同阈值规则去噪的平滑度Fig 4 Smoothness of de-noising of different decomposition levels different threshold rules

2.3 小波基函数的选择

小波基函数的选取对于去噪效果极其重要，正确地选择小波基函数能够使得有用信号与噪声得到充分分离。同傅里叶分析不同，小波分析的基（小波函数）不是唯一存在的。到目前为止，已经构造出的小波基函数有很多，包括Haar小波、Daubechies小波族、Symlets（symN）小波族、Biorthogonal（biorNr.Nd）小波族、Coiflet（coifN）小波族、Morlet小波、Mexican Hat小波、Meyer小波等。实际选择小波的标准主要有以下3种:

1）自相似原则:如果选择的小波与原始信号有一定的相似性，也是在下式的基础上

若χ2j（t）和f（t）有某种程度的相似，则变换后的能量就比较集中，可以有效减少计算量。

2）正交性:选择正交性好的小波基和双正交小波基，有利于航电试验信号的重构。

3）支集长度:大部分应用选择支集长度在5～9之间的小波，因为支集太长会产生边界问题，支集太短消失矩太低，不利于信号能量的集中。

小波函数的主要性质还包括对称性、消失矩阶数和正则性等。一般情况下用某组小波基对信号进行分解得到的小波系数能量集中在少数的几个系数上，则认为这组小波基较好。由于航电试验的测试信号类型不同，根据测试信号（梯形波、锯齿波、方波等）特点引入重构因子来选择小波基函数，这里选用一定阶数的Daubechies（dbN）和Symlets（symN）小波族较合适。

重构信号的能力反映了小波变换对真实信号的提取能力，也即反映了去噪能力的强弱，故引入重构因子对小波基的去噪效果进行评判

定义重构因子

通过向量的2种距离保证消噪信号同原始信号间的整体偏差和局部偏差能够充分暴露出来。如果计算出某小波基的ρ越大，则认为用该小波基进行信噪分离的效果越好。本文中对于两者在重构相对误差中的权重γ1和γ2各取0.5［7～9］。由于已知航电试验的测试信号类型已知，可以通过事先在白噪声下的仿真找出各种类型信号的最优小波基函数。以阶跃特性试验为例，在Simulink中以方波通过二阶系统的输出来仿真标准阶跃信号s，该标准信号分别加入信噪比为10的高斯白噪声模拟含噪输出信号s1，选取通用阈值δ，其中，δ为各层系数的标准差，N为信号的长度，进行5层小波分解阈值去噪得到去噪信号s2。根据式（5）、式（6）选取10种常用的db小波和10种sym小波，计算重构因子如图5所示。

由图5可见，对于航电伺服系统阶跃特性测试信号，sym5和db8小波基的重构因子较大，其去噪效果好于其它小波基，较适用于该类信号的去噪。

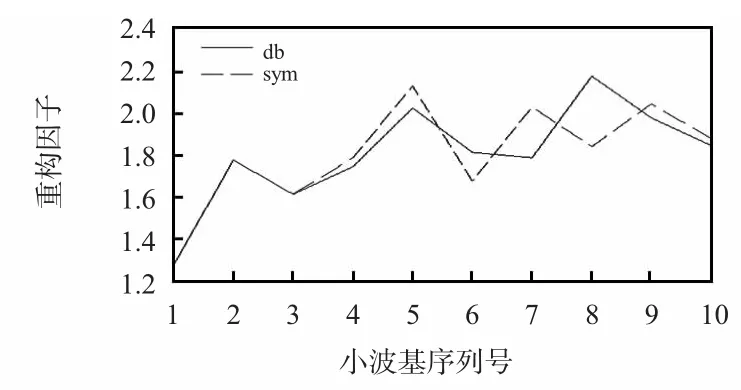
图5 20种小波基对应的重构因子Fig 5 Reconfiguration factor corresponding to 20 wavelet basis

2.4 小波分解层数的选择

由于传感器性能死区测试试验数据去噪是后续数据处理的预处理部分，较好的去噪平滑度便于数据的处理与分析，因此，以去噪平滑度［10］为指标来确定分解层数。

平滑度指标的定义式为

式中f（n）为原始信号，^f（n）为去噪后的信号。

式（7）表明:当数据足够多时，去噪后信号的差分数的方差根与原始信号的差分数的方差根之比，指标r反映了去噪信号的平滑度。

小波分解层数对于去噪效果的影响很大，如果分解层数过少，低频部分的噪声得不到抑制，信噪分离的效果不好，去噪后的信号仍含有较多噪声且平滑度不理想，不便于后期数据处理;如果分解层数过多，去噪效果满意，平滑度理想，但是可能导致去噪后的信噪比下降，同时增大了运算量，图像处理的速度，故选择合适的分解层数非常重要。

以db5小波为例，分解层数分别取2～6，应用启发式阈值（heursure）软阈值去噪方法去噪效果如图6所示。

由图6可以看出:在不同分解层次下，小波阈值去噪的效果有着明显的差异。在4层分解层次以上已经有较好的平滑性，可以进行后续的数据分析了，5，6层分解虽也有不错的平滑性，但在细节保留和运算程度上4层分解更有优势。

表1给出来了图6各层次去噪处理的信噪比、均方差、平滑度3种评价指标，由表中可以看出:几种分解层次的信噪比均方差别不大，难以确定分解层次，但从平滑度上可以看出去噪分解到4层已经足够了。

图6 不同分解层数下的db5小波去噪效果Fig 6 De-noising effects of db5 wavelet of different decomposition levels

表1 不同分解层数下的小波阈值去噪评价指标值Tab 1 Wavelet threshold de-noising evaluating indicator values in different decomposition levels

从以上确定分解层数的讨论可以得出，当小波去噪从信噪比、均方差上不足以确定分解层数时，可以综合考虑平滑度指标作为确定分解层数的依据。

3 结束语

本文给出了传感器性能死区测试实验数据预处理的小波阈值去噪方法，对小波去噪函数的各个参数的选择进行了研究，通过去噪信噪比、均方差和平滑度的比较确定了选择启发式阈值（heursure）的阈值规则，引入了重构因子对小波基函数进行了选择，给出了利用平滑度指标来确定分解层数的方法。对于其它一些试验项目，要根据这些项目试验数据的特点确定各个去噪参数，方法的选择与本文类似。该方法在保证平滑度适宜的基础上，最大程度的保留了信号的细节信息，是一种切实可行的去噪方法。

［1］董长虹，高 志，余啸海.Matlab小波分析工具箱原理与应用［M］.北京:国防工业出版社，2004.

［2］谢 军，李 乐，刘文峰.振动信号噪声消除中的小波基选择研究［J］.科学技术与工程，2011，25（11）:5998-6000.

［3］杜文辽，朱茹敏，李彦明.小波滤波分解层数的自适应确定方法［J］.光电子·激光，2010，21（9）:1409-1411.

［4］Donoho D L.Adapting to unknown smoothness via wavelet shrinkage［J］.Amer Statist Assoc，1995，90:1200-1224.

［5］Donoho D L，Johnstone I M.Ideal spatial adaptation via wavelet shringage［J］.Biometrika，1994，81（3）:425-455.

［6］臧玉萍，张德江，王维正.小波分层阈值降噪法及其在发动机振动信号分析中的应用［J］.振动与冲击，2009，28（8）:58-60.

［7］郭 亚.振动信号处理中的小波基选择研究［D］.合肥:合肥工业大学，2003.

［8］吕唯唯，顾 亮，黄雪涛.小波变换在履带车辆振动信号处理中的应用［J］.噪声与振动控制，2012（4）:141-143.

［9］李月琴，栗 萍，闫晓鹏，等.无线电引信信号去噪的最优小波基选择［J］.北京理工大学学报，2008，28（8）:724-726.

［10］陈 强，黄声亨，王 韦.小波去噪效果评价的另一指标［J］.测绘信息与工程，2008，33（5）:13-14.