MPC算法在机载传感器规划中的应用

张 欢，吴 军，何贵波，吴志峰

（1.空军工程大学航空航天工程学院，陕西 西安 710038;2.中国人民解放军93256部队，辽宁 沈阳 110034）

0 引言

随着任务规划系统的不断发展，人们对机载传感器规划的研究也陆续开展起来，传感器规划用于作战飞机在完成任务执行过程中对自身的机载传感器使用计划的制定，其中包括对传感器的选用、使用时机、使用策略等［1］，并对使用后的效果进行分析，评估达成任务目的的可行性，以此更好地发挥装备的作战效能和完成作战任务。传感器规划与航线规划密切相关，通常是在航线规划完成以后开始实施，以航线中的某个位置作为使用时机开展传感器的使用计划制定工作，当使用时机不能满足既定的目标要求时，需要及时调整使用时机或对航线进行修改。

本文将主要探究在传感器规划过程中如何根据目标的状态来设置传感器的使用时机、使用策略，如何实时跟踪捕捉到目标，以及如何将捕捉到的信息及时反馈回来，以便能够实时地对飞行航线进行局部调整。为此，本文提出了一种改进的模型预测控制（model prediction control，MPC）算法，该算法将传统MPC的基本思想［2］与卡尔曼滤波中的目标状态估计理论相结合，仿真结果表明:该算法在解决传感器探测跟踪移动目标方面具有良好的效果，能够比较准确、快速地搜索到移动目标。

1 MPC基本思想

MPC是20世纪70年代在工业控制领域出现的一种新型控制算法，该算法的基本思想是在每个推进步长中先预测未来的输出状态，然后确定控制动作。在下一个推进步长中重复进行优化过程，并保持原有的优化性能指标不变，改变其作用区域，以此体现MPC算法在线滚动优化特点。常规MPC主要包含3个基本的要素:预测模型、滚动优化和反馈校正［2］。

1）预测模型

预测模型用来表述对象的输入输出动态行为，就是根据对象的历史信息和未来输入来确定对象的未来输出。

2）滚动优化

滚动优化是一种基于优化的控制，通常情况下，是根据某一性能指标的最优来确定未来的控制作用，其数学描述一般为:设预测时域为m个步长，控制时域为n个步长，n≤m，在寻优的过程中，对于任意时刻j，通过上述推进步长可计算出对应的控制序列，直至寻优结束。因此，可定义目标函数为

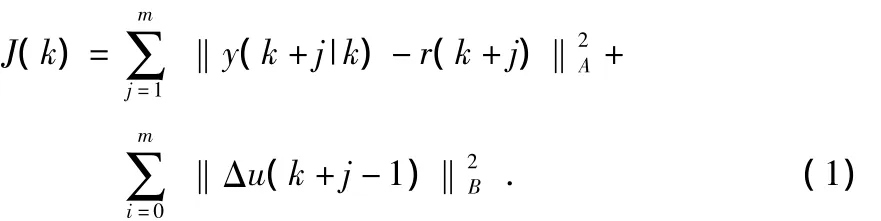
滚动优化实质上是对目标函数在线不断滚动寻优的过程。

3）反馈校正

反馈校正环节用于补偿模型预测误差或其它干扰因素所产生的扰动。

2 算法基本流程

在基于MPC的传感器规划算法中，首先需要做的是构建一个初始搜索图C（D，S），对于任意一点r∈R，在该图中都存在一条边s∈S，满足r∈FOR（s），其中，FOR为传感器能够覆盖到的所有目标探测区域，接下来将利用已有的信息对搜索图进行初始化。假设载机的起始位置为点d0，随机选取3个点d1，d2和d3作为初始任务点，由这4个点构成一条初始航线P=（d0，d1，d2，d3）与相应的传感器计划L（P，0）。在载机沿着初始的航线P从起始点d0飞到任务点d1的过程中，传感器根据初始的传感器计划L（P，0）对目标区域进行探测，并根据探测的结果对目标区域的目标估计信息进行更新。同时计算出未来的飞行航线P=（d1，d2，d3，…，di+3）和对应的传感器计划L（P，i），使得期望的航线收益（P）达到最大。当载机到达任务点d1之后，就以d1作为新的起始点，滚动优化重复以上步骤，直到最终发现目标。最后，分析此次传感器规划过程中传感器的使用效果，并对是否达成作战目的的可行性做出评估分析。

基于MPC的传感器规划算法的具体流程图如图1所示。

接下来主要针对算法流程中的初始搜索图如何构建、传感器计划L的定义、航线收益R（p）的计算、基于卡尔曼滤波理论的目标状态估计模型的建立以及如何分析传感器的使用效果等几个方面进行剖析。

2.1 初始搜索图的构建

在搜索图问题中，以图的顶点表示航线点，2个顶点之间的连线表示一条航段，通常将图整体记为C，将图C中的全体顶点构成的集合记为D，图C中的全部边构成的集合记为S，并记C=（D，S），图搜索问题的本质实际上就是在满足给定约束指标的前提下，在图中寻找出一条最优的航线［4］。如图2所示为一个基本的图模型，其中d1～d9为航线点，s1～s9表示航段，航段未完全标出。

有了基本图模型之后，可根据基本图模型来构建搜索图。在一片搜索区域R上构造一个四边形均匀网格图C=（D，S），网格图C必须满足如下条件:对于搜索区域R内的任意一点r，都有与之相对应的一条边s∈S，能够保证r落在边s上的某些点的传感器可探测区域（FOR）内，由此可以确定图内的任意一点传感器都能够探测到。

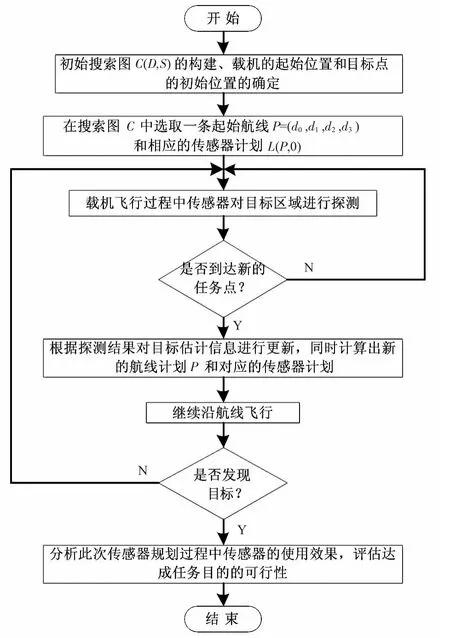
图1 基于MPC的传感器规划算法流程图Fig 1 Flow chart of sensor planning algorithm based on MPC

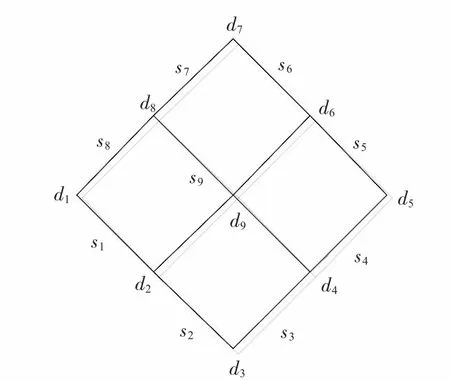
图2 基本图模型Fig 2 Basic graph model

某型作战飞机在执行任务之前，首先需根据已有的先验情报信息对搜索图进行初始化，利用目标状态估计理论所获取的目标信息对网格图C中的目标信息进行初始化。如图3所示为构建的初始搜索图，图上的点d0为载机的初始位置，点d1，d2和d3为预先选取的3个任务点，图上的小黑点为搜索图初始化后目标估计的位置分布情况。

2.2 传感器计划的定义

1）传感器视场（FOV）和观测场（FOR定义）

传感器在地面上的瞬时探测区域称为传感器的视场，即为FOV，观测场FOR则是随着载机的移动和对传感器进行的一些操作，FOV在地面上不断移动，进而形成的载机对地面的全部探测范围称之为观测场［5］。如图4所示为某型机载雷达的探测视场示意图。

图3 构建的初始搜索图Fig 3 Builded initial search graph

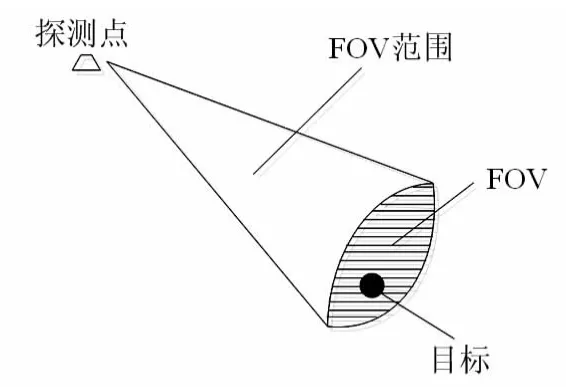
图4 传感器视场FOV示意图Fig 4 FOV diagram of sensor field

由图4可以看出:FOV范围的大小由传感器的探测点和视场大小决定，由于FOV的大小一般由传感器的系统参数决定，并且在一定范围以内其值通常不变，为常数。因此，在研究传感器规划问题中，通常用传感器的观测点来描述传感器规划问题。

2）传感器任务的定义

假设i时刻传感器的观测点为q（i），则指向q（i）的传感器视场定义为FOV（q（i）），一个作用在FOV（q（i））范围内的时延定义为一个传感器任务，记为q（i）［6］。

传感器任务的序列称为传感器计划，一般来讲，一个传感器计划是由多个传感器任务序列组合而成的，属于离散范畴内的对象，因此，可记为

2.3 航线收益计算

定义i时刻传感器的瞬时搜索增益为r（i），其含义实质上为i时刻发现目标的概率，如果一个目标处于传感器的FOV内且被发现了，则收益为1，传感器初始搜索收益为r（0）=0。传感器的下一步搜索收益一般由传感器任务q（i）、当前的目标状态估计值设为x（i）和当前搜索收益决定，其计算式

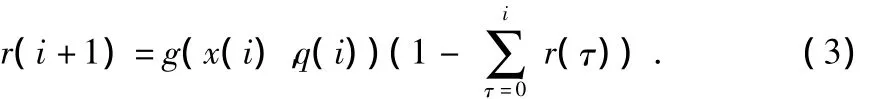
式中 函数g的值为i+1时刻目标被发现的概率。

航线P的收益可定义

式中TP为航线P上所有的可能执行的传感器任务总数，r（τ）为 τ 时刻传感器的搜索收益［7］。

2.4 目标状态估计模型建立

本文采用了卡尔曼滤波器来估计目标的状态分布，卡尔曼滤波是一种经典的、最优估计的递推滤波算法，具有精度高、实时性好的特点［8］。设目标的卡尔曼滤波状态方程

式中 X（k）为k时刻目标的状态向量，X（k）∈Rn，A为k时刻状态转移矩阵，W（k）则是均值为0的高斯白噪声。

假设目标的位置可表示为

式中 f函数表示k时刻目标的真实位置，ΔX（k）则表示误差量，则可将上式用矩阵形式表示为

将公式（7）作为卡尔曼滤波的量测方程，其中C表示状态信号与输出信号之间的增益矩阵。

可进一步求出误差协方差矩阵为

增益矩阵

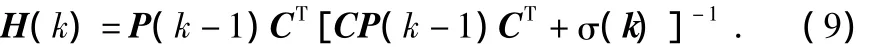
X（k）的状态估计值

测量噪声方差阵为

式（5）～式（11）组成了以卡尔曼滤波理论为原理的目标状态估计模型。

2.5 传感器使用效果分析

在每进行完一次传感器规划之后，应当对此次规划过程中的传感器使用效果进行分析，如图5所示为某机载雷达使用效果分析图。

从上图中可以看出:为了检验机载雷达的使用效果，在雷达规划组件中将用户设置的雷达操控参数、使用时机、载机的即时位置与姿态信息、目标/目标区信息、气象信息等发送到雷达模型，接收其作用范围、可探测度等使用效果的计算结果，并以图形化方式进行直观显示［10］。

分析完MPC算法基本流程中的关键要点之后，接下来通过仿真验证该算法在传感器规划过程中的使用效果、算法的合理性。

图5 机载雷达使用效果分析图Fig 5 Using effect analysis diagram of airborne radar

3 算法仿真验证

仿真实验采用VS2010编程软件，利用之前介绍的图搜索原理，选取了一片50 km×50 km的网格式任务区域，该区域作为传感器对移动目标的搜索区域。假设目标以近似匀速直线方式运动，卡尔曼滤波系统的初始参数设置如下

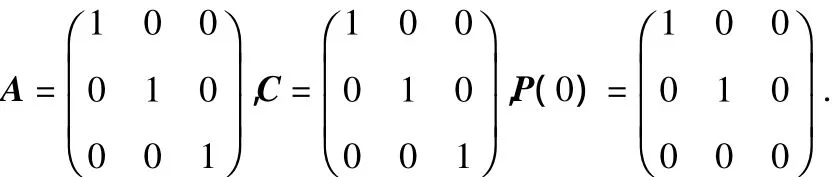
如图6所示为仿真实验效果图。其中，点1为执行任务的载机起飞点，点2、点3、点4、点5、点6为航线点，也即为任务点，在这5个航线点上将载机携带的传感器设备（只考虑机载雷达）也形象的标会了出来;图中的小黑点是利用已有目标先验情报信息，再运用上文中建立的卡尔曼目标状态估计理论，得到的目标状态初始分布;点7（图中三角形）作为机载雷达最终探测到的目标点，在图中只显示了4个点7位置，这4个位置从上到下依次作为在雷达进行探测的过程中目标依次移动的4个位置。

从仿真结果图中可以看出:当目标点在4个点7位置从上到下移动时，机载雷达能够准确地探测到目标移动的位置，达到了对目标实时跟踪的效果。因此，可以得出结论:基于MPC的传感器规划算法在解决移动目标搜索这一关键的传感器规划问题时，能够快速、准确地搜索到移动的目标，基本达到了对目标的实时跟踪效果。

4 结论

本文针对机载传感器规划过程中的移动目标搜索这一难题，将MPC的基本思想与经典卡尔曼滤波中目标状态估计理论相结合，提出了一种基于改进MPC算法的传感器规划方法，在深入剖析了该算法的基本思想和算法流程中的关键要素之后，再通过具体的编程，仿真验证了该算法在解决移动目标搜索这一传感器规划问题中的有效性、合理性。

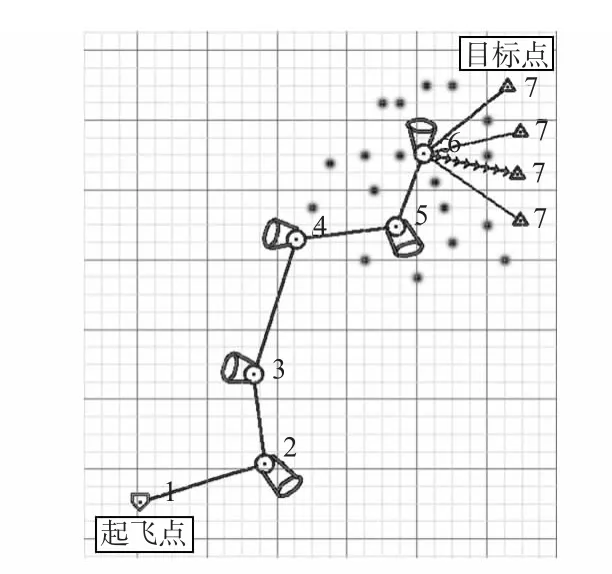
图6 基于MPC算法的传感器规划仿真实验结果图Fig 6 Simulation result diagram of sensor planning based on MPC algorithm

［1］邢立宁，陈英武.任务规划系统研究综述［J］.火力与指挥控制，2006，31（4）:1-4.

［2］王文博.模型预测控制的抗扰性能分析［D］.杭州:浙江大学，2012.

［3］霍德聪.战术飞机打击任务中的传感器使用策略与规划方法研究［D］.长沙:国防科技大学，2007.

［4］Collins G E，Riehl J R，Philip S V.A UAV route and sensor control optimization algorithm for target search［R］.California:University of California，2007.

［5］Skoglar P，Nygards J，Bjorstrom R.Path and sensor planning framework applicable to UAV surveillance with EO/IR sensors［R］.Kista，Sweden:Totalforsvarets förskning sinstitut（FOI），2007.

［6］黄丁才.无人侦察机航线与传感器规划方法研究［D］.长沙:国防科技大学，2009.

［7］周 燕，范 鹏.战术航空侦察航路规划评价模型［J］.电光与控制，2007，14（1）:52-54.

［8］宗长富，胡 丹，杨 肖，等.基于扩展Kalman滤波的汽车行驶状态估计［J］.吉林大学学报，2009，39（1）:7-11.

［9］任 佳，高晓光，赵欢欢.基于目标状态估计的UAV路径重规划决策模型［J］.控制与决策，2009，24（7）:1033-1037.

［10］赵星辰.时间敏感目标的信息处理决策技术研究［D］.西安:空军工程大学，2012.