基于路径规划和输入成型的挠性航天器振动控制方法

刘德庆，彭仁军，张子龙

（上海航天控制技术研究所，上海 200233）

0 引言

为增加成像幅宽，对突发事件地区实现即时观测，或通过卫星沿轨迹方向前视和后视实现立体成像，这对卫星的快速机动能力提出了严格要求［1］。航天器姿态机动方法分为开环和闭环机动。开环机动对模型的确定性要求高，仅用于单轴机动；闭环机动分为阶跃指令和路径规划模式，阶跃指令模式有超调，路径规划模式则可避免超调，且机动过程平缓可靠。最常规的机动路径为基于bang－bang控制的时间最优路径（BCB路径），但跟踪BCB路径易激起挠性附件大幅度振动，影响稳定时间［2］。

挠性振动抑制对航天器的高精度高稳定度控制十分重要，尤其对要求姿态敏捷机动的中小惯量挠性卫星，姿态机动中激起的挠性振动延长了稳定时间，甚至引发故障。目前航天器挠性处理皆采用频率隔离减少挠性对控制器控制作用的影响，未对挠性作抑制处理。当前，对航天器的稳定度和快速性要求高，须对航天器的挠性进行抑制处理。航天器挠性抑制研究基于智能材料、智能结构进行振动主动控制。文献［3］采用压电智能元件粘贴于悬臂梁；文献［4］基于压电元件制动器设计滑模变结构控制器作主动抑振，但基于智能材料抑振法对帆板振动的测量噪声大，精度低，代价高，不适于在轨实现。输入成型法为一种前馈控制法，是指由脉冲序列（输入成型器）与一定的期望输入相卷积，所形成的指令作为系统的输入并控制系统运动。输入成型技术可有效消除或衰减系统残留振动，甚至在系统响应尽可能快时减小系统的超调量［5－8］。为此，本文研究了一种角余弦过渡的角加速度路径规划法，用输入成型技术对其进行优化。

1 问题提出

令I为惯性坐标系，b为航天器本体坐标系，d为航天器目标坐标系。如无说明，本文涉及的矢量均在b系中。

设ω为b系相对I系的角速度；ωd为d系相对I系的角速度，则d系相对b系的误差角速度ωe＝ωd－ω。相应地，令q为b系相对I系的姿态四元数，qd为d系相对I系的姿态四元数，则d系相对b系的姿态四元数qe＝q－1×qd。

考虑挠性附件相对航天器本体固定情形，其受空间干扰和挠性振动影响的卫星动力学模型表示为

四元数运动学模型

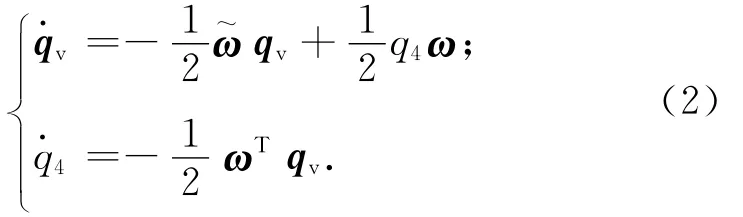
基于路径规划和输入成型的挠性航天器姿态控制描述：规划合适的指令路径，经输入成型后加入姿态控制系统中作为动坐标系d的运动姿态，使依据数学模型式（1）～（3）构造的控制规律u实现b系跟踪d系并抑制挠性振动，亦即t→∞时有qev→0，ωe→0，η→0。

2 路径规划与输入成型

考虑工程执行机构输出和测量装置的量程限制，航天器大角度机动的理想路径是执行机构输出最大力矩加速，达到航天器最大角速度匀速，一段时间后以最大力矩实现减速。因受航天器挠性附件振动影响，直接跟踪以上理想路径易激起挠性附件振动，影响稳定度和快速性。为抑制挠性附件振动，减少稳定时间，提高姿态稳定度，先使用余弦过渡加速度路径，再应用输入成型技术对路径进行优化。

2.1 余弦过渡加速度路径

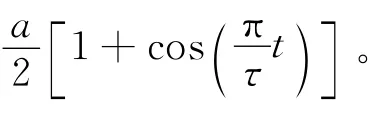
图1 余弦过渡加速度路径Fig.1 Cosine transition acceleration path

具体规划步骤：

b）按工程实际选取τ。

c）依据执行机构输出力矩大小和航天器惯量大小选取a。

d）根据测速装置的量程限制确定匀速段角速度大小ωy，进而确定T＝ωy／a－τ。

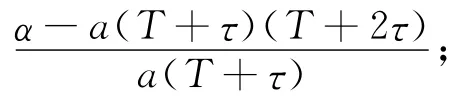
f）由步骤a）将欧拉轴e的方向矢量分配到b系三轴上可得规划的角加速度路径ad。

g）对角加速度矢量路径积分可得ωd；解算运动学方程式（2）可得航天器相对目标姿态的qd。

2.2 多模态输入成型器

式（1）的第二式帆板挠性振动方程针对每个模态和阻尼分别设计成型器，串联作为抑制多模态成型器。

考虑工程实际中挠性模态参数的不确定性，无需在标称频率点严格抑制为零，只要将振动抑制在某一容许的范围即可。独立模态采用文献［10］的双峰EI输入成型器脉冲序列为

式中：

式中：ωi为i阶挠性模态频率；ξi为附件i阶挠性模态阻尼比；F中第一行为脉冲作用时刻，第二行为对应脉冲作用时刻幅值。

对考虑n阶模态的挠性附件的航天器，其多模态双峰EI输入成型器的脉冲序列为

将规划的余弦过渡加速度路径得到的ωd，qd，ad与成型器的脉冲序列相卷积作为目标坐标系d系的运动状态。

3 跟踪滑模控制器设计

滑模控制系统滑动模态运动的稳定性，完全取决于滑动模态的设计，因此只要保证滑动模态方程的稳定性，该阶段的运动一定是稳定的。一般的滑模控制，系统初始时刻不在滑模面上，需要设计控制律驱使系统状态从初始点进入滑动模态。对跟踪规划轨迹的机动方法，初始姿态与规划路径的起点误差为零，以误差信息构造的滑模控制系统初始点在滑模面上，跳过了进入滑模面的过程，只需控制系统状态在滑模面上运动，就可跟踪规划轨迹，实现姿态机动。

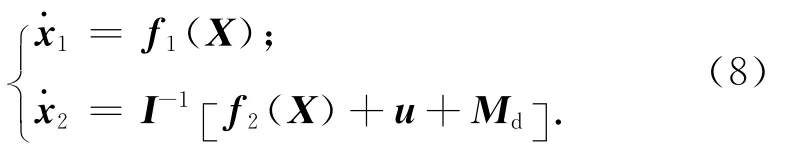
设计Terminal滑模面

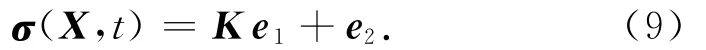
式中：K为常值对角阵。

故控制器是渐进稳定的。

为减少不连续符号函数sgn（σ）引起的抖动，用变参数切换函数

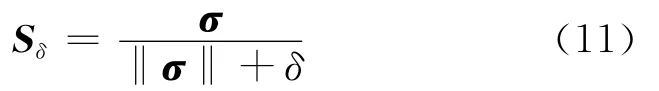
替代sgnσ［11］。此处：δ为误差e1，e2的函数；δ0，δ1为正的常数。

最终得到控制器

4 仿真

用Matlab／Simulink软件对挠性航天器姿态机动方法仿真验证。取挠性航天器相关参数为

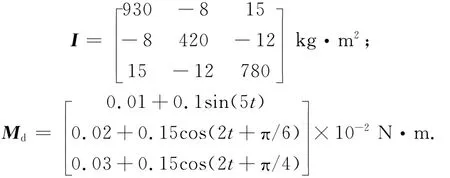
挠性附件考虑帆板的前四阶挠性模态，其振动频率矩阵和阻尼比矩阵分别为

耦合系数矩阵为

对姿态机动控制，目标姿态相对参考坐标系是固定的，以目标姿态的本体系为参考坐标系，直接给出初始姿态相对目标姿态的初始值信息为

路径规划采用参数为a＝0.005 4rad／s2，ωy＝0.034 9rad／s，τ＝ 1s。 控 制 器 参 数 为K＝diag［1.9 1.7 2.3］，δ0＝0.001，δ1＝0.045，D＝5。

采用控制器（13）跟踪双峰EI输入成型优化后的余弦过渡加速度路径，仿真结果如图2～5所示，达到0.000 5（°）／s稳定度所用时间为50.69s，实现了机动控制且抑制帆板挠性振动。

图2 相对目标姿态四元数Fig.2 Relative quaternion to object attitude

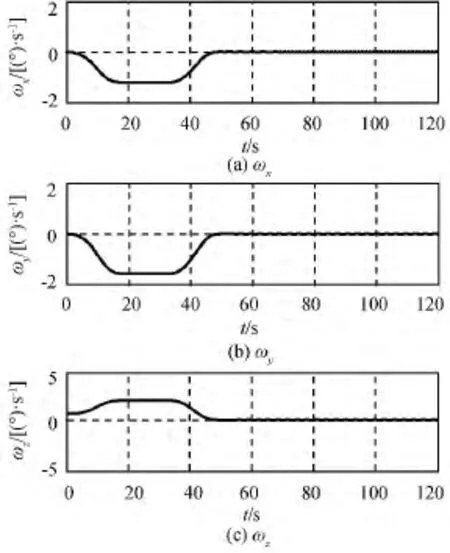
图3 姿态角速度Fig.3 Attitude angle velocity

对跟踪指令轨迹的机动方法，机动过程分为跟踪段和稳定段。跟踪段是指令轨迹未达到目标值，指令驱动姿态机动的阶段；稳定段是指令轨迹不再运动后直至航天器达到相应稳定度的稳定控制阶段。采用跟踪指令轨迹的航天器姿态机动稳定时间包括跟踪段和稳定段时间。具较大挠性的航天器稳定段时间的减少取决于挠性附件振动的抑制情况，抑振目的是实现姿态机动进入稳定段后挠性附件作用于航天器本体的残余耦合力矩小。

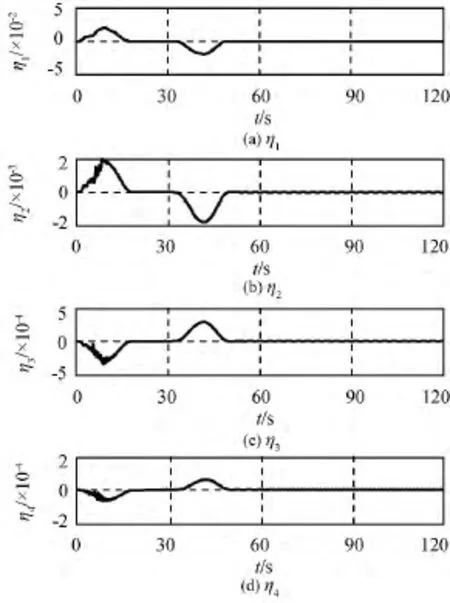
图4 帆板挠性模态Fig.4 Flexibility mode of sail board

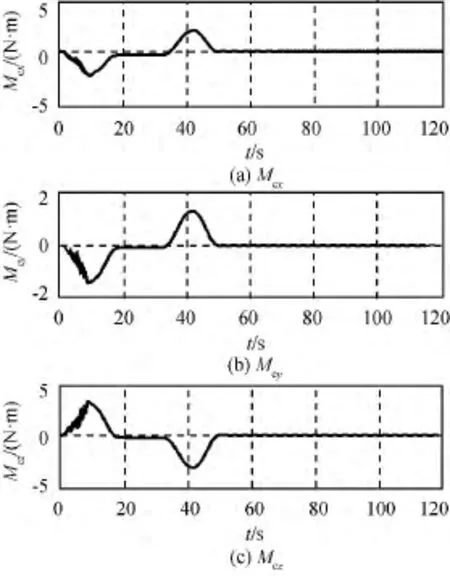
图5 指令力矩Fig 5 Control moment

对挠性耦合不大的航天器姿态机动，不使用输入成型，而是延长余弦过渡加速度路径的过渡过程，抑振效果较好。为说明余弦过渡加速度路径抑制挠性振动的有效性，将其与跟踪BCB路径的机动方案进行比较。

比较以下三种方案：BCB，规划BCB路径，用控制器式（13）跟踪；CTA，规划余弦过渡加速度路径（τ＝5），用控制器式（13）跟踪；CTA＋IS，规划余弦过渡加速度路径（τ＝1），采用输入成型器式（7）进行优化，用控制器式（13）跟踪。三种方案在50s后进入稳定段，仿真所得稳定段50～80s的帆板挠性模态坐标、残余耦合力矩、指令力矩及整个机动过程的指令力矩如图6～9所示。

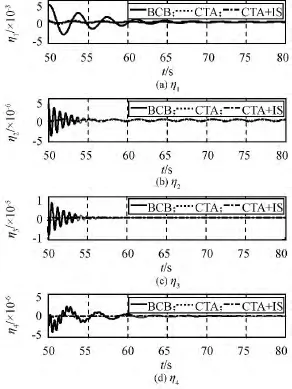
图6 帆板模态坐标（50～80s）Fig.6 Flexibility mode at 50～80s

对三种方案仿真结果中挠性相关的各项指标进行数据分析，见表1，其中3σ＝2×10－5（°）／s。

表1 三种方案仿真结果Tab.1 Simulation results of three mtehods

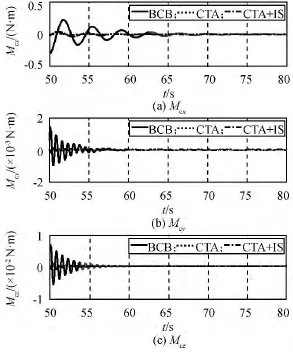
图7 帆板残余耦合力矩（50～80s）Fig.7 Residual coupling moment at 50～80s

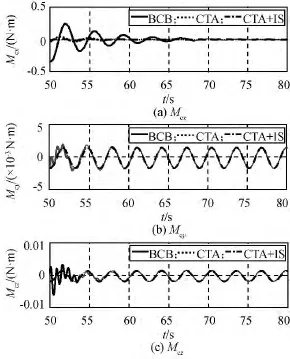
图8 指令力矩（50～80s）Fig.8 Control moment at 50～80s

机动50s后进入稳定段控制过程，CTA，CTA＋IS方案的挠性模态较BCB方案显著减小，对本体几乎无残余耦合力矩，因采用CTA路径使跟踪机动后帆板对本体的残余耦合力矩较小，跟踪CTA路径较BCB路径50s后最大残余耦合力矩小一个量级，跟踪输入成型器优化的CTA路径残余力矩再有一定减少。BCB方案在41s进入稳定段控制，至83.2s实现2×10－5（°）／s的稳定度，稳定段时间长，相反，CTA，CTA＋IS方案对帆板挠性振动有抑制作用，稳定段时间较短。

图9 指令力矩对照Fig.9 Comparison of control moment

5 结束语

本文通过对常规BCB路径的改进，提出了余弦过渡加速度路径，挠性耦合较大时还可输入成型技术对其优化。使用跟踪滑模变结构控制器仿真分析，并与跟踪BCB路径方案对比，以跟踪经输入成型技术优化的余弦过渡加速度路径方案对挠性附件振动抑制效果明显，稳定时间短。

［1］ 杨保华.航天器制导、导航与控制［M］.北京：中国科学技术出版社，2010.

［2］ 郑立君，郭 毓，赖爱芳，等.挠性航天器大角度姿态机动路径规划［J］.华中科技大学学报（自然科学版），2011，39（S2）：232－235.

［3］ 胡庆雷，马广富.改进型正位置反馈＿变结构卫星姿态主动控制［J］.振动工程学报，2007，20（4）：324－330.

［4］ 周连文，周 军，李位华.挠性航天器姿态机动的主动振动控制［J］.火力与指挥控制，2006，31（6）：31－34.

［5］ SINGER N C，SEERING W P.Pre－shaping command inputs to reduce system vibration［J］.Journal of Dynamic Systems，Measurement，and Control，1990，112（1）：76－82.

［6］ PARMAN S，KOGUCHI H.Controlling the attitude maneuvers of flexible spacecraft by using time－optimal／fuel－efficient shaped inputs［J］.Journal of Sound and Vibration，1999，221（4）：545－565.

［7］ HU Qing－lei.Input shaping and variable structure control for simultaneous precision positioning vibration reduction of flexible spacecraft with saturation compensation［J］.Journal of Sound and Vibration，2008，68（3）：18－53.

［8］ 原劲鹏，杨 旭，杨 涤.输入成型在卫星喷气姿态机动控制中的应用［J］.南京：东南大学学报（自然科学版），2005，11（35Ⅱ）：137－142.

［9］ 雷拥军，谈树萍，刘一武.一种航天器姿态快速机动及稳定控制方法［J］.中国空间科学技术，2010，30（5）：43－53＋58.

［10］ SINGHOSE W E，PORTER L J，SINGER N C.Vibration reduction using multi－hump extra－insensitive input shapers［C］／／Control System Society：Proceedings of the American Control Conference.Seattle：［s.n.］，1995：3830－3834.

［11］ 胡剑波，庄开宇.高级变结构控制器理论及应用［M］.西安：西北工业大学出版社，2008：78－79.