一种改进的长码直扩信号捕获算法研究

李春萍，李 菊，刘晗超，于 翔

（上海航天电子技术研究所，上海 201109）

0 引言

在直扩系统中，长码扩频较短码扩频具有更好的隐蔽性、抗截获性和更强的抗侦察能力。随着航天扩频测控技术的发展，扩频码的选择不仅局限于短的伪随机码，多种长周期的扩频码也被用于实际工程［1］。但长码扩频意味着系统有更高的伪码周期，受信道特性影响增大，系统的同步更难，同步时间更长。针对长码直扩信号捕获，减少信号的捕获时间是关键［2］。目前常用的长码快捕技术主要有间接捕获和直接捕获两大类。间接捕获技术指传统短码引导长码的捕获技术；直接捕获技术主要有并行多通道长码直接捕获法、扩展复制重叠法（XFAST）、CCPAZP－FFT长码直捕法等。分析发现，并行多通道长码直接捕获法占用的资源最多，抗干扰性能不佳；CCPAZP－FFT长码直捕法结构复杂，占用存储资源较多；扩展复制重叠法结构较简单，抗干扰性能较好，捕获时间较少，但相关性较差［2－5］。为减少捕获时间，提高捕获性能，本文在扩展复制重叠法基础上进行改进，对重叠段进行平均化处理，提出了一种新的长码直扩信号解决方案——扩展复制平均重叠法。

1 扩展复制平均重叠法基本原理

将本地伪码的子序列相加（或折叠）构造一折叠母序列，然后与输入序列相关，这样可覆盖一个大的时间不确定度，从而加快对时间不确定度的搜索。XFAST利用了该技术和伪码子序列的互相关特性，其基本原理可概括为：根据接收信号的伪码序列长度L（为2的幂次方），在扩展M段（M≥2且为正整数）的情况下，产生长度M×L的本地伪码序列，对M个子码序列进行叠加处理，将此叠加后的序列与接收信号进行相关处理；当出现高于判决门限的相关峰值时，再分别将M个子码序列与接收信号进行相关计算，判断出接收信号中的实际伪码相位。此方法可使FFT计算量减少为原来的1／M，并将搜索的不确定区域扩大M倍。当子序列长度L与M的比值大到数百甚至数千时，计算量明显减少，相关次数的量级从M×L减少为L＋M。

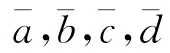
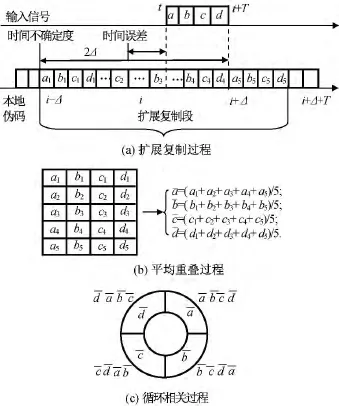
图1 扩展复制平均重叠法原理Fig.1 Algorithm principle of extended replica average folding acquisition search

由图1，假设从时间t至t＋T进来的信号有码片a，b，c，d共4个，对输入信号的到达时间，只有t＾，Δ，为覆盖整个不确定搜索区间，本地伪码产生从－Δ至＋Δ＋T的伪码序列。如图1所示，扩展码复制有5段，之后进行平均化处理，每段有4个码片（ai，bi，ci，di），这5段折叠成一个母序列，有4个新码片

2 改进型长码直扩信号捕获系统方案

用扩展复制平均重叠法，建立长码直扩信号捕获系统方案，如图2所示。

图2 长码直扩信号捕获系统Fig.2 Principle of long code DS signal acquisition system

由图2可知：长码直扩信号捕获系统工作流程如下。

a）输入信号先经过载波剥离，再进行FFT计算。

b）取M段本地伪码子序列（码片长度为L个码片）进行平均叠加，计算FFT共轭值。

c）对两者的乘积进行IFFT计算。

d）通过求模选大操作，选出相关峰值中的最大值，与门限值比较。若大于设定门限值，则进行去模糊度计算，获得具体的伪码相位捕获值；若小于设定门限值，则在搜索完所有多普勒频点后，取一M段子序列重复计算，直至搜索完所有伪码相位和多普勒频率范围。

其中：去模糊度计算类似于上述计算过程。本质上，扩展复制平均重叠法可形容为在FFT快捕计算中嵌套一细化FFT快捕计算。

3 改进型长码直扩信号捕获系统仿真

用 Matlab软件对本文方案进行仿真验证［6－7］。取仿真初始条件为：长码码长256×1 023chip，码速率10.23Mc／s，采样频率58.08MHz，取4段折叠，子序列码长1 023chip，子序列采样4 096点，初始伪码相位100 000chip，多普勒频率66 000Hz。对上文建立的长码直扩信号捕获系统进行仿真，多普勒步进值5kHz，长码直扩信号捕获系统的二维搜索结果如图3所示，去模糊度的二维仿真结果如图4所示。

图3 取平均时搜索重叠段和多普勒频率Fig.3 Search overlapping segments and Doppler frequency while taking average

由图3、4可知：搜索到多普勒频率段位于37个区间内的第32个区间（即正多普勒频率段的第13个区间），根据多普勒搜索步进值，可知最终捕获的多普勒频率为65 000Hz，预设的多普勒频率值为66 000Hz，两者相差1 000Hz，在±2.5kHz频差之内。经过去模糊度之后，捕获到的伪码相位为99 999.75chip，预设的伪码相位为100 000chip，两者相差0.25chip，符合1／4个码片的理论误差。

图4 取平均时去模糊度Fig.4 Clear ambiguity while taking average

4 改进型长码直扩信号捕获系统性能

基于扩展复制平均重叠法的长码直接捕获法利用M个子码序列（本设计中选4段叠加），可减小FFT的计算量，并扩大时间不确定范围。当本地伪码序列很长时，此算法可极大减少FFT的运算次数。但因互相关性能不理想性，叠加次数受限，叠加次数越大，背景噪声也越大。因此，需根据实际情况合理选取叠加次数和每次运算的点数。

设一多普勒频率，通过FFT算法进行时域伪码相位搜索时间为TFFT，重叠段数为M次，固定子码序列长度为L，多普勒搜索的频点数为N，则对码长Lcode的长码直扩信号，捕获的时间

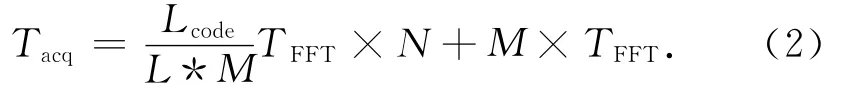
在本设计中，系统的单次处理时间为TFFT。取N＝37，固定子码序列长度L＝1 023个码片（子码序列只是长码序列中的一段，为满足2的整数次幂，需对其进行内插抽取），Lcode＝256×1 023个码片，不同重叠段数M的捕获时间均不同：M＝16时，Tacq＝608TFFT；M＝8 时，Tacq＝1 192TFFT；M＝4 时，Tacq＝2 372TFFT；M＝2时，Tacq＝4 738TFFT。

由此可知，重叠段数越大，捕获时间越少，但重叠段数不是越大越好，需针对具体的长码选择。

研究扩展复制重叠法发现，如果对重叠后的码序列进行一个取平均的操作，可改善捕获中的峰均比。

在前文仿真条件下，仅改变重叠段的段数，不对重叠段取平均时通过仿真搜索重叠段和去模糊度时的相关峰值和峰均比，结果见表1。表中：相关峰值1为搜索重叠段时所有相关值中的最大值；峰均比1为搜索重叠段时相关峰值1与所有相关值的平均值的比值；相关峰值2为去模糊度时所有相关值中的最大值；峰均比2为去模糊度时相关峰值2与所有相关值的平均值的比值。

表1 不取平均时不同重叠段数对应的相关峰值和峰均比Tab.1 Different number of overlapping segments corresponding peak and PAR while taking no average

同理，不改变其他仿真条件，对重叠段进行平均处理。仿真所得搜索重叠段和去模糊度时的相关峰值和峰均比见表2。

表2 取平均时不同重叠段数对应的相关峰值和峰均比Tab.2 Different number of overlapping segments corresponding peak and PAR while taking average

比较表1、2可知：扩展复制平均重叠法和扩展复制重叠法进行长码直接捕获的特性如下。

a）相同处

与其他长码直接捕获方法相比，可直接捕获长码直扩信号，减少直接捕获时间；选择重叠段数越多，本地信号与输入信号的相关性越差，峰均比损失也越大。

b）不同处

经平均叠加处理，峰均比变化的规律性较明显，表现为递减性；如不取平均，因其叠加效果，相关性变化的规律性变化有一定的随机性。如对重叠段取平均运算，在搜索重叠段数时，虽相关峰值变小，但相应峰均比获得改善；选取合适的重叠段数，峰均比可改善3.15dB（此处M＝4）。改变重叠段数不影响去模糊度计算时的相关峰值和峰均比。

5 结束语

本文对一种改进的长码直扩信号捕获算法进行了研究。通过改进扩展复制重叠法，采用扩展复制平均重叠法，选择子码序列码片长度为1 023chip（抽取采样后为4 096点），取8段进行平均重叠，实现码长256×1 023chip、码速率10.23Mc／s的长码直扩信号捕获。经方案设计和仿真可知：扩展复制平均重叠法在大幅减少长码直扩信号直接捕获时间的同时，搜索扩展段时相关运算的峰均比有改善。

［1］ HEGARTY C.GPS原理与应用（第二版）［M］.寇艳红（译）.北京：电子工业出版社，2007.

［2］ 戴明艳.跟踪与数据中继卫星系统长码同步技术的研究［D］.合肥：安徽大学，2006.

［3］ 张新波.卫星导航接收机中长码直捕算法研究与FPGA实现［D］.成都：电子科技大学，2008.

［4］ 金 璐.GPS卫星定位系统中的P码直接捕获技术研究［D］.西安：西北工业大学，2006.

［5］ 于晓明，郭高峰.GPS P码直接捕获方法研究［J］.海军航空工程学院学报，2007，22（3）：348－345.

［6］ 杨 俊，武奇生.GPS基本原理及其 Matlab仿真［M］.西安：西安电子科技大学出版社，2008.

［7］ 张志涌.精通MATLAB6.5版［M］.北京：北京航空航天大学出版社，2004.