重视教学拓展提升，焕发学生思维光芒

李春华

《新课程标准》指出：教师是教学中的引导者和组织者，同时也是教材与学生联系的纽带。拓展提升有利于教师和学生的发展，有利于教材功能的充分发挥，对学生思维能力的培养起着十分重要的作用。结合自己平时的教学实践，在课堂教学中，数学拓展提升可以从以下几方面着手：

一、探究新知识拓展提升，引导学生大胆思维

往往一个新知识并不是孤立出现的，新知识常常依赖于旧知识。在旧知识的基础上，通过比较它们的内在联系，从而对新知识有一定的了解和掌握。

案例1：对苏科版九年级上册“一元二次方程”第一课时教学时，我给出以下问题：

1.你能说出5x=-17是何种方程？（老师要关注学生对“元”和“次”的理解）

2.它的一般形式是什么？（老师要关注ax+b=0中“a≠0”条件的重要性）

3.你能说出x2-4x+3=0是何种方程吗？（老师仍要关注学生对“元”和“次”的理解）

4. 你能仿照（2）中的说法，说出一元二次方程的一般形式吗？（老师要关注ax2+bx+c=0中“a≠0”条件的重要性）

这些问题的设计，可以让学生用自己的知识经验发现问题，并通过对比和联想，自然地把已有的学习方法流畅地迁移到新知识的学习中，进而总结出一般的规律。引导学生组织讨论，交流分析，获得对新概念、问题的全面认识。在新知识的教学时，这样的拓展设计，重视了学生在课堂上的主体地位，充分调动学生学习的积极性，对学生数学思想和能力的培养有着重要意义。

二、利用变式教学拓展提升，引领学生主动思维

叶圣陶曾经说过：教是为了不教。其中“教”就包含要教会学生独立自己思考，引导学生的思维由浅入深，拓展学生思维的宽度与深度。

案例2：学习《三角形的中位线》后，变式巩固练习。

1.依次连接矩形各边中点所得图形是什么？（将矩形改为四边形、其他特殊平行四边形呢？）

2.依次连接某四边形的各边中点所得四边形是矩形，那么原来的四边形是矩形吗？为什么？

如果中点四边形改为正方形、菱形、平行四边形，那么原来四边形的形状又分别是什么呢？

题1根据性质直接得出结论;题2需要学生逆向思维，把握思维的准度，拓展思维的域度。给学生思考时间和空间讨论问题：中点四边形的形状由什么来确定的？经过师生共同探究，发现：中点四边形的形状与原来四边形的对角线有关，与原来四边形的形状无关。这样既夯实了对结论的理解，又提升了学生的思维。

三、巧用学生的错误分析拓展提升，增强学生自悟思维

问题是数学的心脏。学生出现错误是正常的。我们要勇敢接受、重视，它也是一种学习提升重要的财富资源。

案例3：已知一次函数 y=（k-1）x+k的图像不经过第三象限，则k的取值范围是什么？

此题大部分学生理解错误。原因是没有深刻理解“不经过”的意思。经过画图，学生才明白“不经过第三象限”包含经过一二四象限和二四象限两种情况。找到错误的根源，就可以对症下药。

数学教学是一个动态的过程，注重教学策略的变化，把学生学习中的错误作为学生纠错训练的机会，利用学生“自发”的资源，同样可以开发学生思维。

四、结合跨学科知识拓展提升，搭建思维新平台

案例5：近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知400度近视眼镜镜片的焦距为0.25m，则y与x的函数关系式为（   ）

此题以物理知识为载体，应用数学反比例函数知识为工具，学生通过综合思考，很快得出结果。数学是基础学科，是一种学习工具。有些学科用数学的视角审视科学问题，自觉应用数学知识及其思想方法，让科学学科和数学紧密联系，进而使学习事半功倍。

五、联系实际生活拓展提升，焕发思维新光芒

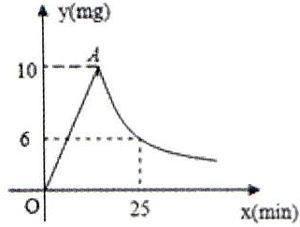
案例6：已知药物在燃烧机释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所示（即图中线段OA和双曲线在A点及其右侧的部分），根据图像所示信息，解答下列问题：

（1）写出从药物释放开始，y与x之间的函数关系式及自变量的取值范围;

（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？

这是一道应用题，学生感到生活与数学紧密联系的，比较亲切。此题涉及方程、不等式和函数思想，学生要具备较强的数学思维能力，才能分析问题和解决问题。真正体现数学在生活中的价值，让学生体会到数学的功能，感悟自己成功的愉悦。

数学教学拓展提升，可以拓宽学生的探究思路，开阔学生的知识视野，培养他们的创造意识和实践能力。同时还能增强学生变式能力，提升学生探究问题的热情和兴趣。通过课堂与实际生活的联系，学科之间的有机结合，数学的内容会更丰富，数学思维也会更活跃。由此可知，拓展提升学生对培养学生发散性思维和开放性意识，有着十分重要的作用。

（作者单位：江苏江阴市第二中学）