固体运载器大气飞行段内弹道优化设计研究

梁欣欣，李世鹏，陈 阳，张 艳，傅 瑜

（北京宇航系统工程研究所，北京100076）

在满足一定的固体发动机总体性能的设计约束下，内弹道决定了发动机推力大小的变化趋势，飞行程序角则决定了推力方向，将二者联合寻优，可使固体运载器的总体方案和飞行程序更加优化［1－4］。在开展固体运载器总体设计的初步论证过程中，普遍将发动机内弹道以平均推力曲线形式来开展发动机的设计与总体方案论证。事实上，平均推力曲线形式的内弹道设计对于实现射程指标以及大气飞行段姿控稳定、载荷条件等并非最优。本文旨在探寻固体运载器具有较好性能时的发动机内弹道曲线形式，在实际工程研制过程中可通过发动机药柱设计来改变药柱燃烧过程中的燃面，获得有利于运载器总体性能的曲线形式。

本文以射程最大为目标，用离散化方法建立了内弹道优化设计模型，并开展了内弹道优化仿真，在满足飞行过程中的姿控和载荷约束的同时，提高固体运载器的射程。

1 数学模型

1.1 飞行程序设计

固体运载器飞行程序采用目前通常使用的工程设计方法［5］。在主动段，运载器垂直起飞一段时间后，利用攻角转弯段调整推力的方向，此后进入攻角为0的重力转弯段，在减小气动损失的同时，达到弹道转弯的目的，然后进入定轴俯仰程序角飞行段。被动段为无动力椭圆轨道飞行段。固体运载器主动段俯仰飞行程序角曲线如图1所示。

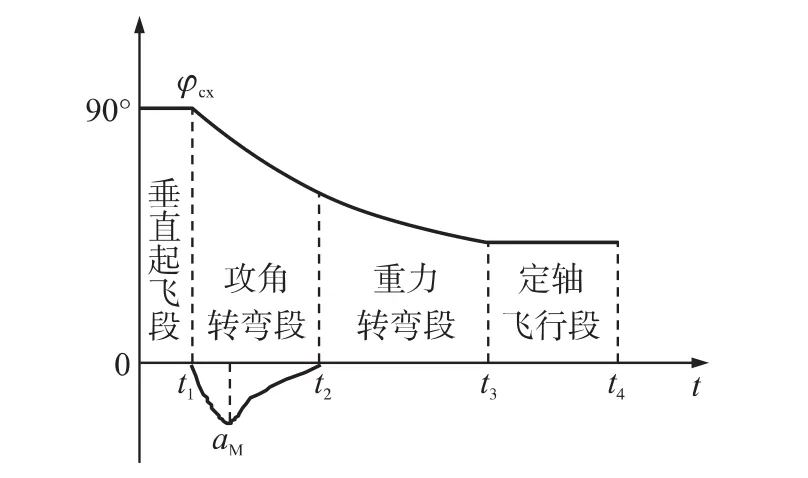
图1 固体运载器主动段俯仰飞行程序角曲线

图1 中，t1可由运载器推重比确定，t2在运载器飞行亚音速段结束，重力转弯段可在大气稀薄时的某一高度结束。通过以上程序角设计原则，推力方向的变化仅与攻角转弯段的最大负攻角αM有关。

1.2 飞行动力学建模

在方案论证阶段，可将固体运载器的运动视为质点运动，在发射坐标系内建立质点弹道模型［6－7］。固体运载器运动学方程为

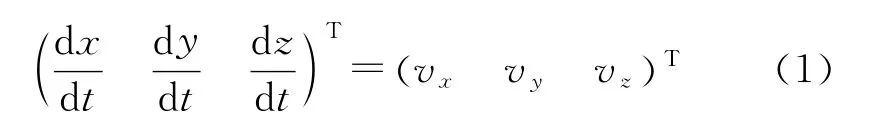
式中：x，y，z为运载器位置在发射系的坐标；vx，vy，vz为速度在发射系的分量。

动力学方程为

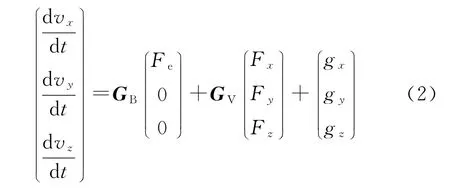
式中：GB为弹体系到发射系的转换矩阵；GV为速度系到发射系的转换矩阵；Fx，Fy，Fz分别为气动阻力、升力和侧力；gx、gy、gz为引力在发射系的分量；Fe为发动机的有效推力，按下式计算：

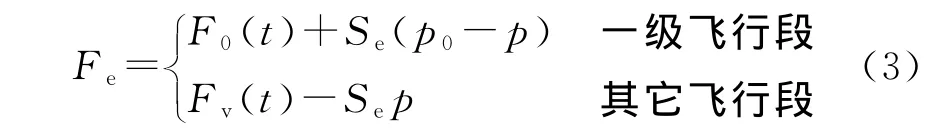
式中：F0（t）为发动机地面推力，Se为发动机喷口面积，Fv（t）为发动机的真空推力，p为大气压强，p0为地面大气压强。

气动力按下式计算：

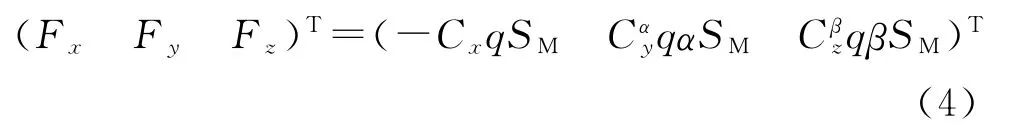
式中：Cx为阻力系数，Cαy为升力系数对攻角α的导数，Cβz为侧力系数对侧滑角β的导数，SM为固体运载器特征面积，q为动压。

地球采用静止圆球假设，因此引力可按下式计算：

式中：g沿地心矢径方向，可根据角度关系获得发射系分量gx，gy，gz；μ为地球引力系数；r为地心矢径。

质量按下式计算：

式中：m为运载器实时质量，m0为各级起飞质量，为各级发动机的质量流量。

2 优化模型及求解方法

2.1 优化模型

本文建立推力曲线的假设条件：①发动机装药量、总冲、工作时间保持不变；②内弹道推力与压强、流量成正比；③不考虑发动机上升沿与下降沿的曲线变化；④不考虑内弹道曲线的变化导致的发动机总重的变化。

将内弹道推力曲线离散化为多个结点，将每个结点上的推力值作为优化变量，然后采用拟合方法获得整个内弹道推力曲线。

离散及拟合方法在轨迹优化的各类算法中应用较为广泛，本文采用等时间间隔离散、线性拟合方法。将发动机工作时间为T的内弹道推力曲线F（t）离散化为等时间间隔的N段，N＋1个时间节点上的推力值分别为F0，F1，…，FN，n＝1，2，…，N，则曲线F（t）可利用时间节点上的推力值线性拟合获得，即：

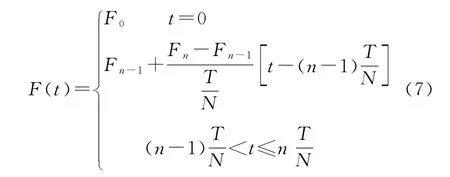
推力结点值F0，F1，…，FN和最大负攻角αM构成了优化问题的优化变量。发动机总冲为定值，且推力结点值受发动机承压影响需在一定范围内变化，即构成了优化问题的约束条件。综上，可建立以最大射程为优化目标的内弹道优化模型，如下所示：

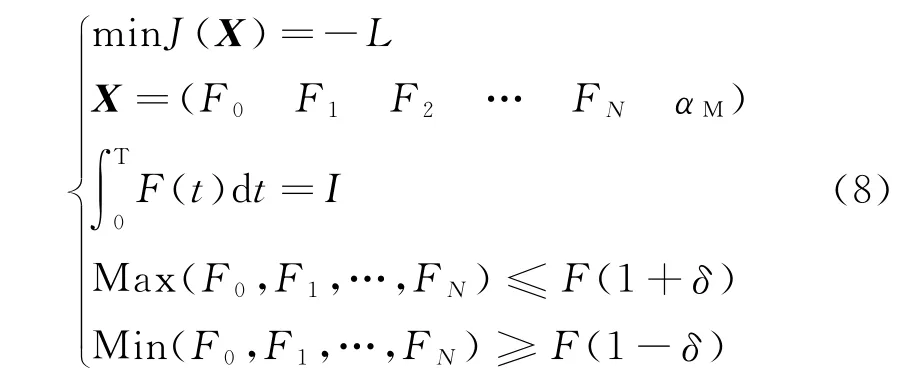
式中：J（X）为目标函数，X为优化变量，L为射程，I为发动机总冲，F为平均推力，δ为平均推力上下浮动的百分比，可根据发动机可承受压强确定。流量的计算可根据与推力成正比的关系计算得到。

为了将上述带约束的优化问题转化为无约束的优化问题，将待优化的各节点推力值进行等比调节和值域调控的迭代处理，使得约束自动满足。无约束的优化模型为

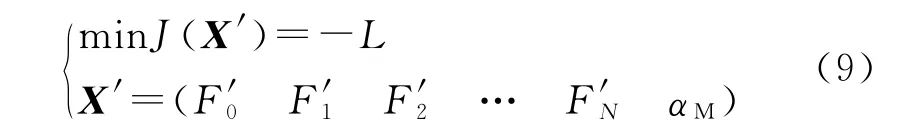
将带约束的优化问题（8）转换为无约束问题（9）的流程，如图2所示。

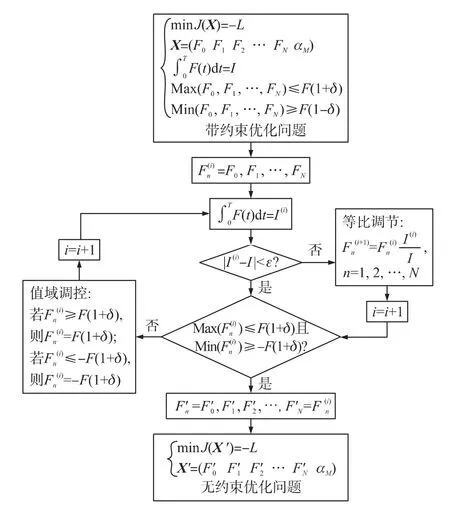
图2 带约束的优化问题转换为无约束问题的流程图

2.2 优化流程

针对优化模型，可将攻角转弯段的最大负攻角利用一维搜索获得优化值，其余优化变量利用成熟的优化算法进行优化。针对优化模型（8）的仿真优化流程如图3所示。

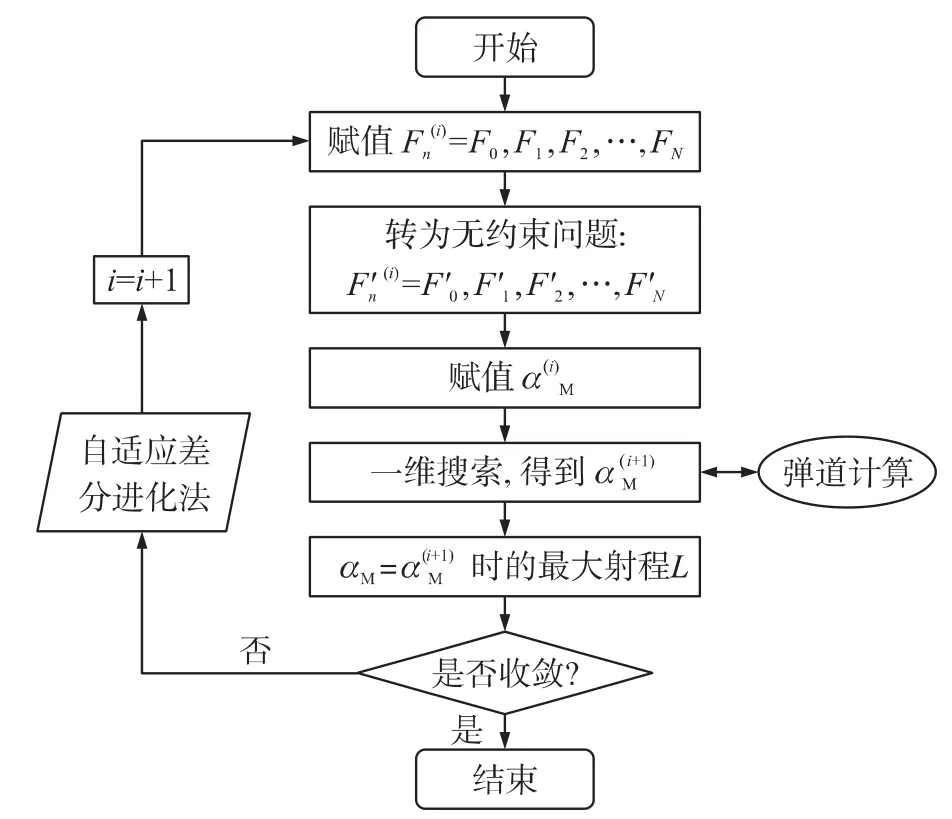
图3 离散法优化流程

2.3 优化算法

本文采用自适应差分进化法［8－9］进行优化求解。1）基本思想。

自适应差分进化法的基本思想为：针对种群中个体适应度的分散程度进行度量，并利用个体的适应度及其分散程度进行交叉和变异操作，用种群熵表征种群搜索过程中的收敛程度，并根据种群熵的变化自适应地减小种群的搜索范围，即在搜索初期快速减小种群的搜索范围，提高早期收敛的快速性；随着搜索的进行，逐步降低种群搜索范围减小的速度，以保证全局收敛性能，避免局部收敛。

2）基本操作。

设种群规模为m，设Fmin和Fmax是在搜索过程中第k代种群的最小和最大适应度值，将适应度值划分为等距的m个Aj（j＝1，2，…，m）区域：

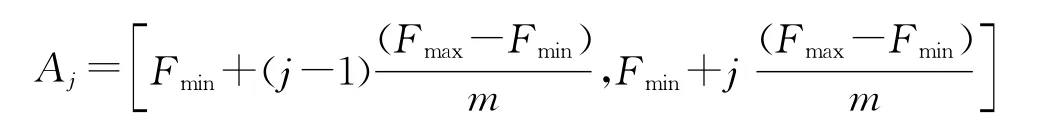
设种群中有mj个个体的适应度值属于Aj区域，定义个体出现在Aj区域的概率为Pj＝mj／m。由此，定义第k代种群的熵为设krc、S分别为初始种群或改变范围后种群的代数和熵，kmax为最大的设定代数，定义SR为是否改变种群范围的控制参数：SR＝0.98exp（－krc／kmax）。

设优化变量xj∈ ［，］，j＝1，2，…，m，和分别为第k代种群中适应度值前60%的个体的第j个变量的最大值和最小值。当Sk／S＜SR时，改变种群搜索的范围：

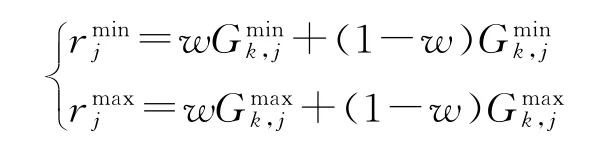
式中：w为松弛因子。在搜索初期，SR较大，保证算法快速缩小种群的搜索范围，提高搜索效率。随着搜索的进行，SR逐渐变小，种群搜索范围缩小的速度减缓，以保证算法的全局收敛性。

3）算法流程。

自适应差分进化法的流程如图4所示。

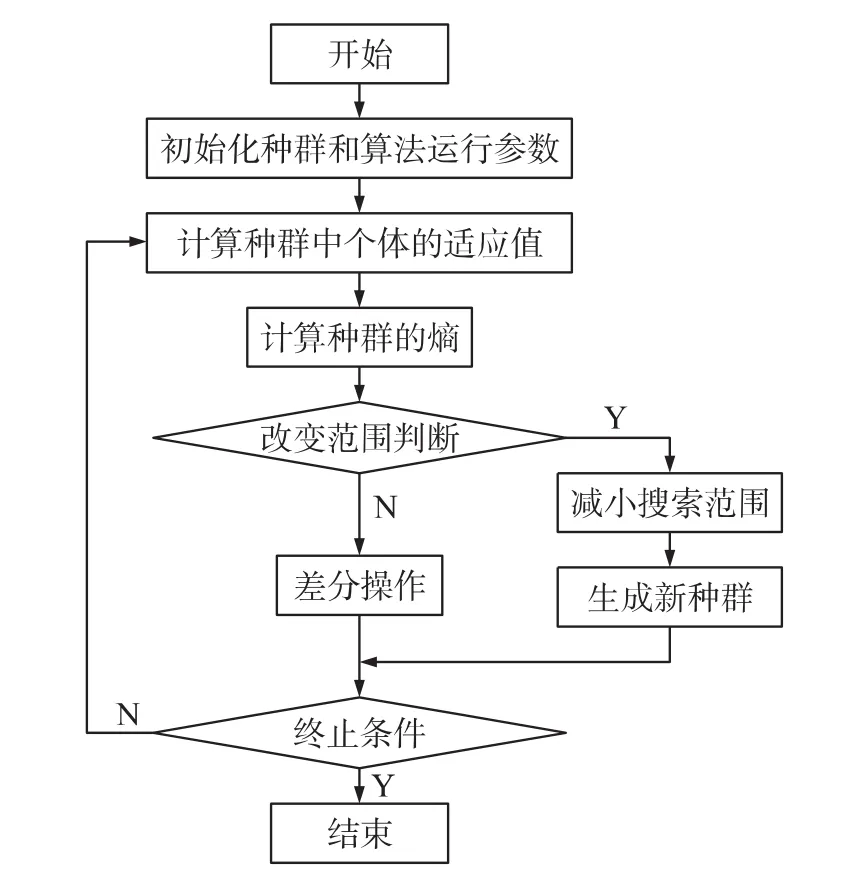
图4 自适应差分进化算法流程图

3 优化结果及分析

针对典型三级固体运载器大气飞行段开展分析。对于载荷条件，由于该飞行器一级飞行段不是最恶劣载荷环境，其最大动压提高30%依然满足载荷条件；对于姿控条件，一二级分离的高度尽可能高，一二级分离动压尽可能小，则对姿控条件越有利。

利用自适应差分进化法开展离散模型的优化。将一级发动机工作时间等间隔分为24段，以25个节点值作为优化变量，最优转弯攻角αM在25个节点值确定后由一维搜索算法获得，δ＝0.3，即F（t）内弹道曲线各节点值上、下限分别设定为平均推力值的130%和70%。种群规模为40，迭代收敛最大代数为200代。

优化迭代收敛曲线如图5所示，得到的优化内弹道曲线如图6所示，优化结果与平均推力对比如表1所示。图5中，Lmax为每代最大射程值，表1中以平均模型为基准给出了各量优化后的变化百分比，L为射程，qmax为最大动压，Hs为一二级分离高度，qs为一二级分离动压。

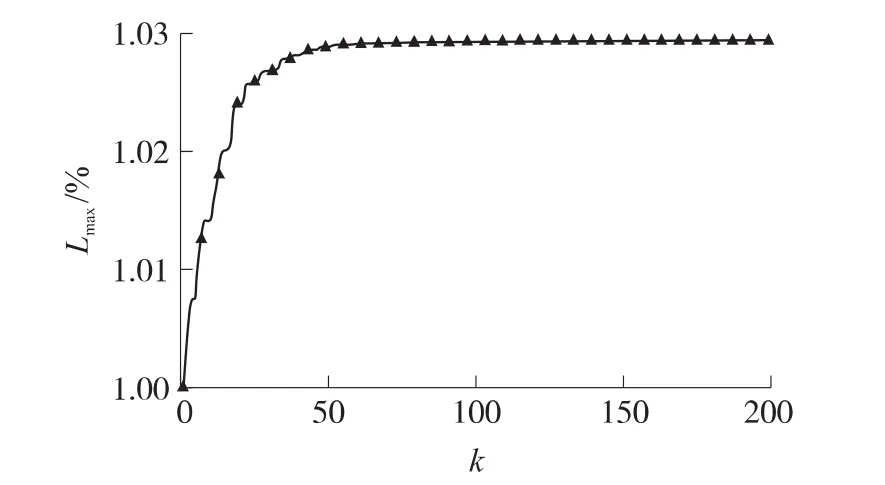
图5 优化收敛曲线

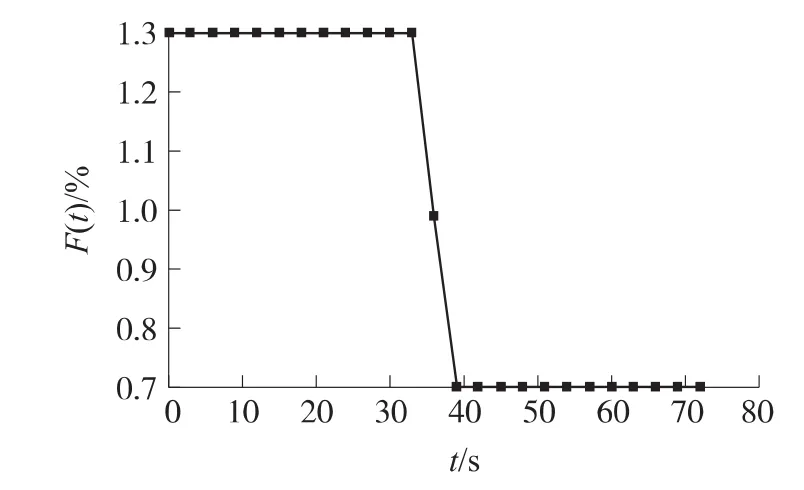
图6 优化内弹道曲线

表1 优化结果与平均推力对比

由图表可知，“前高后低”的双推力内弹道曲线对于提高射程来说具有积极意义，可提高射程约3.1%；同时，由于跨音速段推力大，导致最大动压提高27.1%，小于可承受最大动压；一二级分离高度提高为115.6%，分离动压减小为37.8%，这对于姿控分离稳定十分有利。因此，在固体运载器方案论证时，可针对“前高后低”的双推力内弹道形式对大气飞行段工作的发动机开展研究论证工作，保证在符合发动机性能约束和运载器飞行载荷环境约束的情况下，提高射程能力，改善一二级分离环境。

4 结论

本文以固体运载器为研究对象，针对大气飞行段内弹道优化设计建模，并以自适应差分进化法进行仿真验证。通过对仿真结果的分析，有以下几点结论：①将内弹道及外弹道联合优化，可进一步改善固体运载器的整体性能和飞行环境；②内弹道曲线优化形式并非传统认为的平均推力形式；③“前高后低”的双推力的内弹道曲线形式对于提高射程和改善飞行环境具有积极意义。

研究成果可为固体运载体总体方案论证提供借鉴意义。

［1］JAROSLAW S S.Sensitivity analysis and multidisciplinary optimization for aircraft design：recent advances and results［J］.Journal of Aircraft，1990，27（12）：993－1001.

［2］BROWN N F，OLDS J R.Evaluation of multidisciplinary optimization techniques applied to a reusable launch vehicle［J］.Journal of Spacecraft and Rockets，2006，43（6）：1 289－1 300.

［3］BRAUN R D，POWELL R W.Comparison of two multidisciplinary optimization strategies for launch－vehicle design［J］.Journal of Spacecraft and Rockets，1995，32（3）：404－410.

［4］杨军，陈汝训，赵锡良.战术火箭／固体火箭发动机一体化优化设计［J］.宇航学报，1999，20（1）：21－27.YANG Jun，CHEN Ru－xun，ZHAO Xi－liang.Integral optimization design for tactical rocket and it’s SRM by utilizing the synthesis of internal ballistics and trajectory［J］.Journal of Astronautics，1999，20（1）：21－27.（in Chinese）

［5］龙乐豪.总体设计［M］.北京：中国宇航出版社，1989.LONG Le－hao.Overall design［M］.Beijing：China Astronautic Publishing House，1989.（in Chinese）

［6］贾沛然，陈克俊，何力.远程火箭弹道学［M］.长沙：国防科技大学出版社，1994.JIA Pei－ran，CHEN Ke－jun，HE Li.The ballistics of long－range rocket［M］.Changsha：National University of Defense Technology Press，1994.（in Chinese）

［7］洪蓓，梁欣欣，辛万青.固体运载火箭多约束弹道优化［J］.导弹与航天运载技术，2012，（3）：1－5.HONG Bei，LIANG Xin－xin，XIN Wan－qing.Multi－constraint trajectory optimization for solid launch vehicle［J］.Missiles and Space Vehicles，2012，（3）：1－5.（in Chinese）

［8］PRICE K.Differential evolution：a fast and simple numerical optimizer［C］／／Biennial Conf of the North American Fuzzy Information Processing Sociey.New York：IEEE 1996：524－527.

［9］PRICE K.Differential evolution vs.the functions of the 2nd ICEO［C］／／IEEE Int Conf on Evolutionary Computation.Indian Upolis：IEEE，1997：153－157.