基于落点预测补偿的激光末修弹脉冲点火相位研究

李兴隆，王晓鸣，姚文进，吴 巍

（1.南京理工大学 智能弹药国防重点学科实验室，南京210094；2.中国人民解放军63863部队，吉林 白城137001）

脉冲控制激光半主动末段修正弹在弹道末段，与弹体捷联的激光探测器接收目标反射的激光信号，通过弹载处理器得到目标相对弹丸的方位信息。由控制策略决定脉冲点火时机和点火相位，通过脉冲力的作用，达到修正弹道偏差，提高命中精度的目的。

Jitpraphal T［1］分析了比例导引、抛物线比例导引和弹道追踪导引律的点火相位，能显著减小落点散布，但3种导引律分别需要弹丸速度矢量旋转角速度信息、弹丸和目标相对位置信息和弹丸实时位置信息。杨荣军［2］根据目标偏差量得到脉冲方位角，但是需要跟踪检测系统测算弹丸到目标纵向和横向的偏差量。寇保华［3］根据目标视线转率在弹体坐标系上的分量确定发动机推力方向，也需要由导引头测出目标视线的转率。程振轩［4］分析了弹体追踪法下，由激光探测器得到的目标方位角作为脉冲力作用角，并没有考虑弹丸剩余飞行距离。

文中基于激光探测器和落点预测补偿，推导出在弹体追踪导引律下的末修弹脉冲点火相位表达式，仅需激光探测器和弹体转速信息，不仅节省了各种测量传感器带来的成本，而且获得了较好的命中精度，符合低成本高精度智能弹药的发展趋势，具有可观的发展前景。

1 无控落点与目标偏差距离

1.1 激光探测器模型

在弹道末段，当目标进入探测器作用范围内时，由目标反射回来的激光信号会被捷联在弹体上的激光探测器（典型的有四象限探测器）捕获到。不同方位的目标所反射的激光光斑在探测器上的象限也不一样，因此可由探测器得到目标相对弹丸的方位信息，如图1所示。

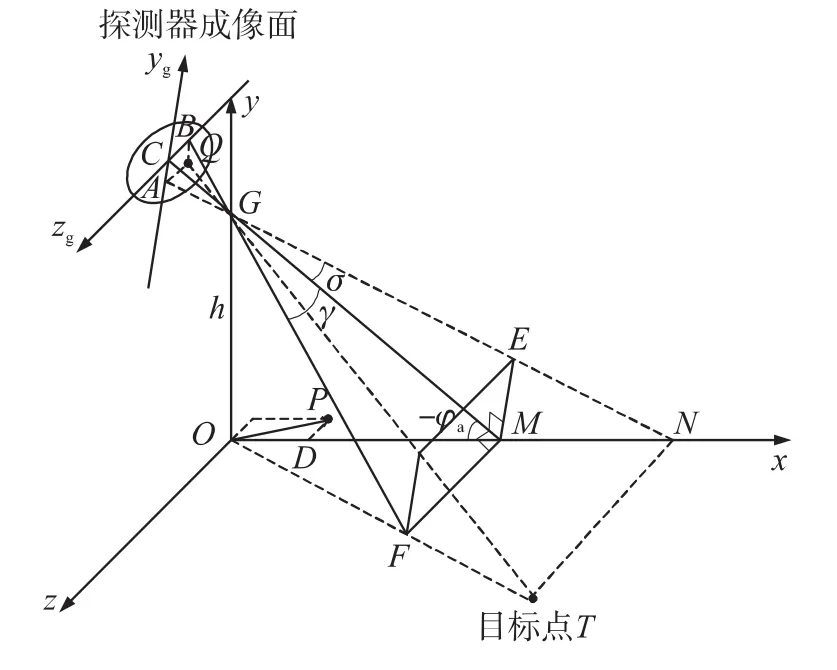
图1 目标相对弹丸位置

图1 中G为弹丸质心，T为目标点，Q为目标点在探测器上的成像点，由几何关系可得：

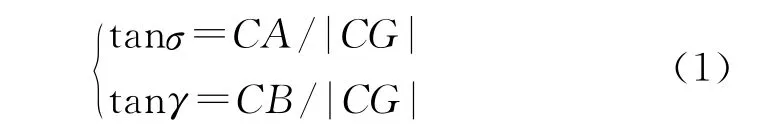
式中：｜CG｜＝f为成像焦距；σ，γ分别为目标相对弹丸的高低角和方向角；σ＞0表明目标在激光探测器光轴与地面交点的前方，反之目标在后方；γ＞0表明目标在弹丸纵轴所在铅垂平面的右侧（从弹体尾部向前看），反之则在左侧。根据这两个角度和几何关系可得到目标点T相对于弹丸的位置：

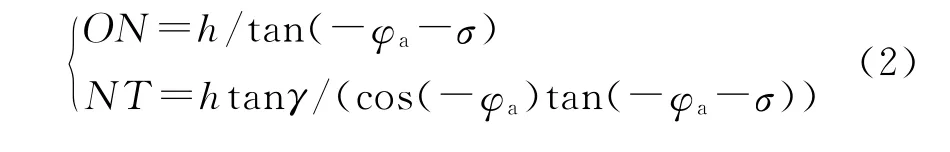
式中：h为此时弹丸的高度，φa为弹轴高低角。

1.2 落点预测补偿

在弹丸发射前，通过计算得到能准确命中目标的理想弹道数据，并存储至弹丸中［1，5］，建立弹丸飞行时间t和弹丸剩余飞行距离（ΔX0，ΔZ0）的函数［6］。在弹道末段，弹丸探测到目标，由控制策略决定启控时机，将此刻时间t0代入到f（t）中得到理想弹道剩余飞行距离，用此距离来作为实际弹丸预测得到的剩余飞行距离，如图1中OP。由于弹丸在发射和飞行过程中会受到各种随机因素的扰动，因此必定会偏离理想弹道，实际落点与理想弹道落点有偏差，但相对整个弹道而言，末段弹道距离很短，因此这种简单的末段弹道落点预测方法误差不大。将启控时刻目标相对弹丸的距离减去无控弹丸预测的飞行距离即可得到需要借用脉冲发动机得到的待修正距离，即弹丸无控落点与目标点实际的偏差量，如下式：

式中：lOD，lDP分别为从启控时刻开始，预测的无控弹丸射程方向和偏流方向剩余飞行距离向量；lΔx，lΔz分别为射程方向和偏流方向的待修正距离向量。

2 脉冲点火相位的确定方法

激光半主动末段修正弹传统点火相位［4］是根据探测器得到目标方位角来确定修正力方向，并没有考虑弹丸剩余飞行距离，也没有分析不同脉冲力作用方向对纵向和横向修正能力的不同，虽然也能朝着目标的方向修正，减小一定脱靶量，但效果不佳。

2.1 脉冲力对纵向和横向的修正能力分析

脉冲发动机采用周向布置，且轴向位置通过弹丸质心。当脉冲发动机点火后，脉冲射流喷出，对弹体产生作用力，由于脉冲燃烧时间极短，通常为几ms到几十ms，可认为弹丸速度瞬间发生改变。脉冲力对弹道的修正本质是对速度的修正，显然，脉冲力作用下弹丸轴向和偏流方向速度的改变量是不同的，所以对弹丸纵向和横向的修正能力也不一样。因此，分析脉冲在2个方向上的修正能力对研究脉冲点火相位很有必要。

定义弹体坐标系Ox1y1z1，Ox1为弹轴，Oy1和Oz1轴固连在弹体上并与弹体一同绕纵轴Ox1旋转。定义基准坐标系OxNyNzN，它是由地面坐标系平移至弹体质心而成，随质心一起平动。定义弹轴坐标系Oξηζ，Oξ轴为弹轴，Oη轴垂直于Oζ轴指向上方，Oζ轴按右手法则垂直于Oξη平面指向右方。图2为脉冲发动机周向布置示意图，其中F为脉冲作用力，其矢量方向与弹轴坐标系中Oη轴的夹角δ为脉冲力作用相位角，点火相位角为τ＝δ＋180°，对应于5号脉冲发动点火。

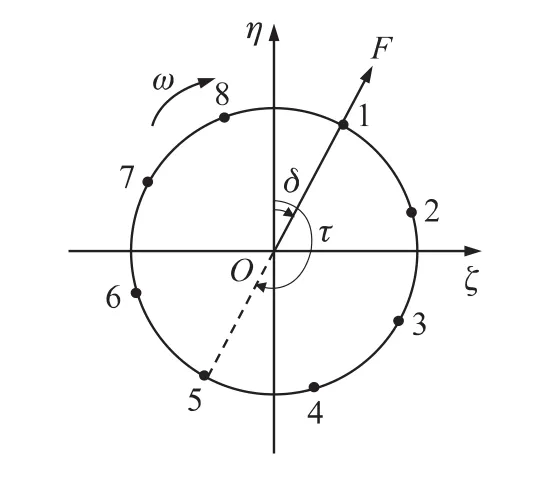
图2 脉冲发动机周向布置示意图

图3 为弹轴坐标系Oξηζ与基准坐标系OxNyNzN的转换关系。

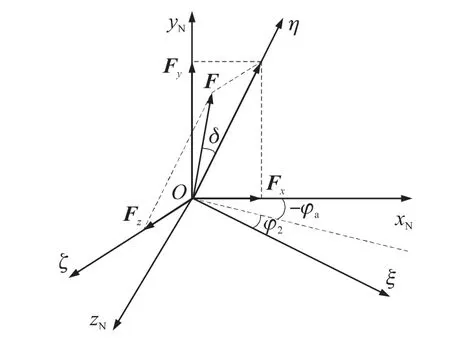
图3 脉冲作用力在基准坐标系下的分量

弹体坐标系与弹轴坐标系只相差一个滚转角φ，为研究方便可视为脉冲力F作用在弹轴坐标系上，则其在基准坐标系下3个轴上的分量Fx，Fy，Fz为

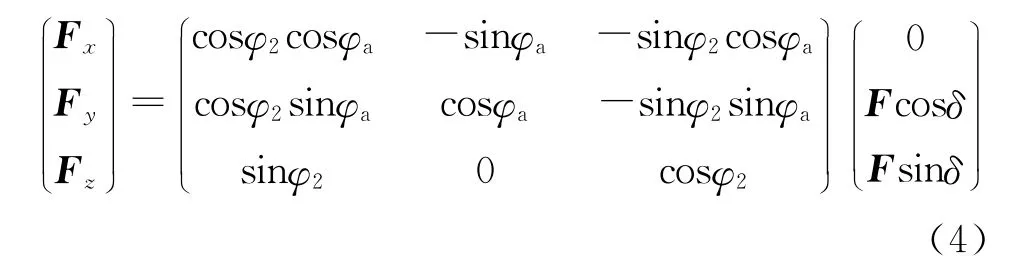
式中：φa，φ2分别为弹轴高低角和弹轴方位角。脉冲力的分力作用在各个轴上，每个轴上的速度分量会发生变化，忽略次要因素，各轴速度增量为［2，7］

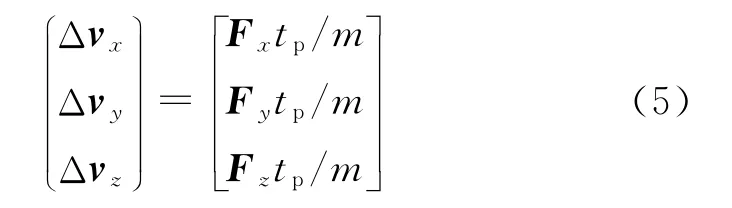
式中：tp为脉冲作用时间，m为弹丸质量。注意到Fx，Fy，Fz均为矢量，因此各轴速度增量也为矢量。脉冲发动机的总冲量I＝Ftp是已知的，再结合式（4）、式（5）可得到各轴的速度增量大小。纵向和横向的速度增量随脉冲力作用角度不同而改变，因此最终的修正能力也不同。

2.2 点火相位角的确定

脉冲修正力作用于弹体后造成的结果是：①铅垂方向速度大小的改变使弹丸飞行时间发生变化，导致落点的变化；②射程方向和偏流方向的速度大小改变，直接引起落点变化。

在铅垂方向，气动阻力和重力占主导地位［8］，末修弹启控后剩余飞行时间为

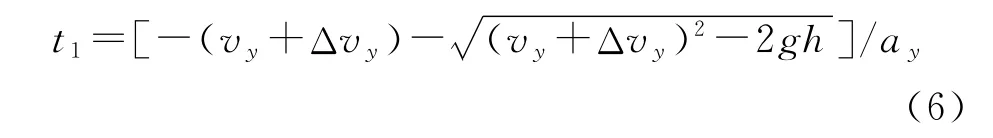
式中：ay为弹丸所受到合力在铅垂方向产生的加速度，ay＝ ［vzρSCD／（2mv）］＋g，v为 弹 丸 速 度 大小。图4为速度坐标系Ox2y2z2与基准坐标系OxNyNzN的转换关系［9］，θa，ψ2分别为速度高低角和速度方向角，弹丸速度在基准坐标系下的分量vx，vy，vz为

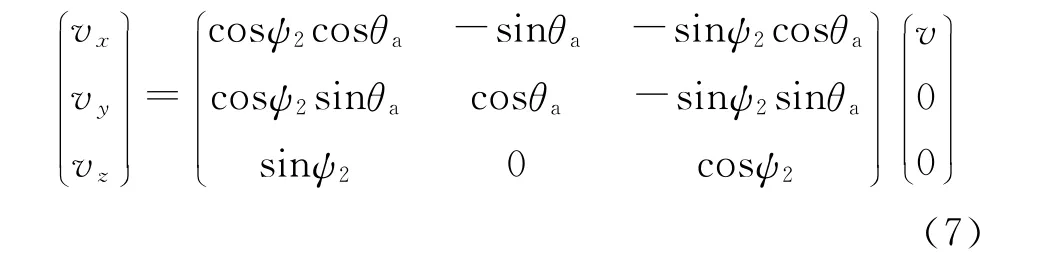
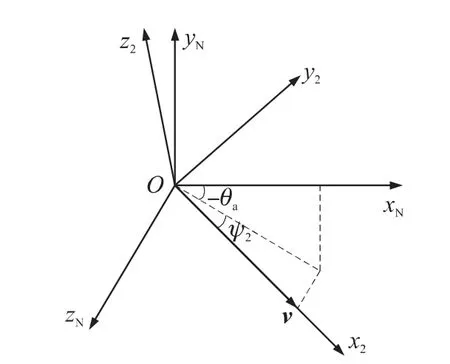
图4 速度在基准坐标系下的分量

末段弹道从启控开始到弹丸落地的飞行时间很短，大约在2～4s内，在此过程中，纵向和横向的速度大小变化不大，可近似为匀速运动，则启控后弹丸的飞行距离为X1＝（vx＋Δvx）t1，Z1＝（vz＋Δvz）t1，则弹丸由于脉冲力作用实际的净修正量为ΔXp＝X1－ΔX0，ΔZp＝Z1－ΔZ0。由于末段修正效果不仅与点火相位有关，而且与启控时机和脉冲冲量大小有关，这里不考虑启控时机对修正量的影响，脉冲冲量大小与修正距离近似成线性关系［10］，对于不同的脉冲冲量大小对应不同的修正能力可引入修正能力系数K。若点火相位选择适当，对于给定的脉冲冲量，弹目实际偏差量与脉冲力净修正量的关系可表示为

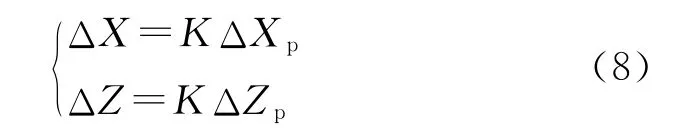
在理想的启控时机下，脉冲冲量大小恰好使脉冲力的净修正量等于弹丸与目标的实际偏差量，即K＝1，文中即基于以上假设。将以上相关参数代入到式（7）中得到：

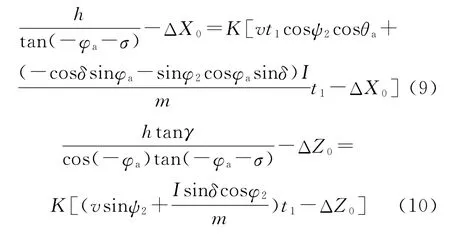
将式（9）、式（10）整理后相除，可消去K，由于速度方向角和弹轴方位角都很小，因此可近似认为cosψ2≈1，sinψ2≈ψ2，cosφ2≈1，sinφ2≈φ2，通过整理得到：

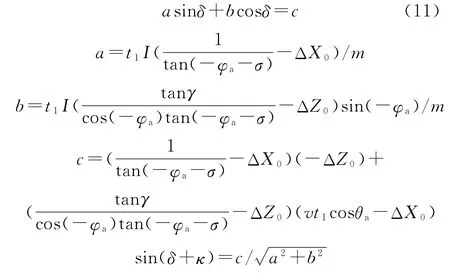
式中：κ＝arctan（b／a）为中间变量，由以上方程可解出脉冲力作用方向角δ，由于目标可能在不同的方位，因此δ∈［0，2π］，可根据成像点在探测器上的不同象限来确定δ的值：

由式（12）可知：

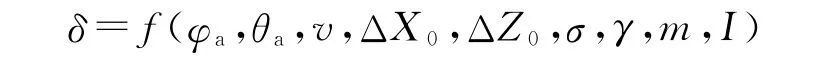
式中：φa，θa，v，ΔX0，ΔZ0可由理想弹道进行估计，σ，γ是由激光探测器直接测出，m，I是已知量。因此，对应特定方位的目标，有唯一的点火相位τ＝δ＋180°与之对应。

3 仿真验证

以某型末段修正弹为研究对象，弹丸质量为13.45kg，初速为340m／s，发射角为45°，在标准气象条件下进行六自由度弹道仿真，文中采用8级脉冲发动机控制，单个脉冲冲量为30N·s［5］，持续作用时间为10ms。在弹道末段，弹丸探测到目标，由控制策略决定启控后，根据前文分析确定点火相位角，当每个脉冲发动机转到点火相位时依次点火，即可进行弹道修正。因此，将点火相位代入到脉冲控制力的修正弹道模型［11］中，可进行末段修正弹道仿真研究。

3.1 点火相位原理验证

为研究单个弹道对于不同方位目标的修正效果，以发射角θ＝45°的无初始扰动的理想弹道为研究对象，在弹道落点O周围每隔45°均匀布置8个目标，如图5中A，B，C，D，E，F，G，H所示，每个目标与无控落点的距离均为80m，依次进行末段修正弹道仿真，可得到单个弹道对不同方位目标的修正效果，如图5。

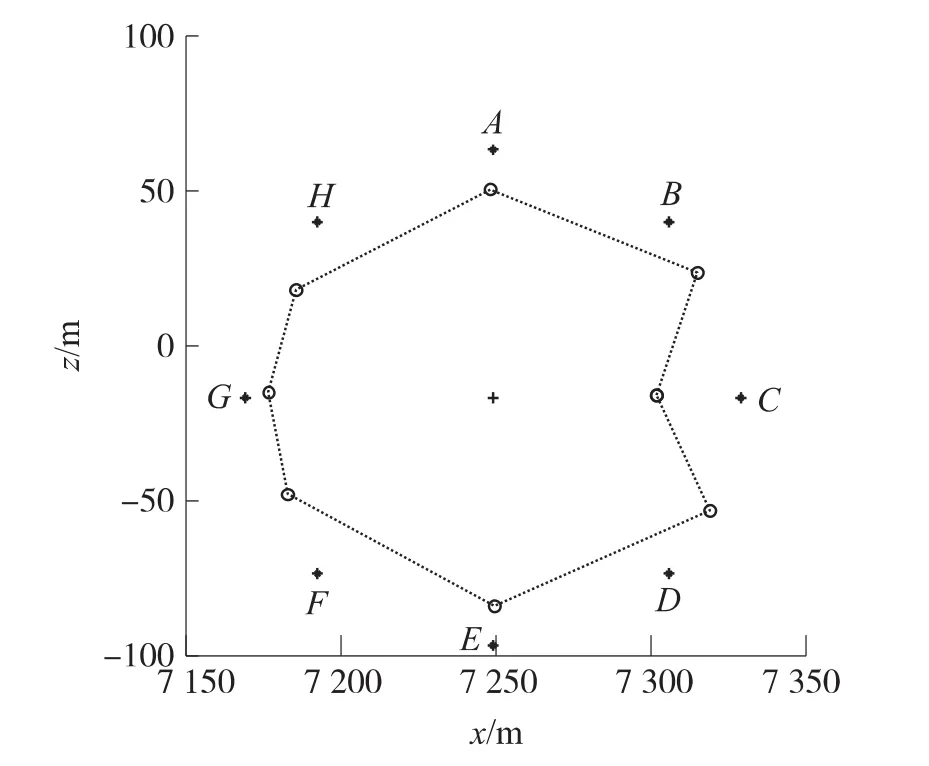
图5 不同方位的目标与弹道落点

由图5得知，修正弹道的落点基本上朝着目标点靠近，说明点火相位方向判断基本正确。统计各个方向的脱靶量大小，可得到末修弹对各个方位目标的修正能力，如表1所示。表1中，δ为脉冲力作用角度，τ为点火相位角，R0为修正前脱靶量，Rt为修正后脱靶量，表1中结果显示正后方、正右方和正左方的修正效果较好，最优可将脱靶量减小到8.25m，修正后8个方向上平均脱靶量为19.31 m，比修正前减小了75.86%，可见修正效果已经很显著，说明脉冲点火相位角的选择比较理想，符合精确打击的要求。

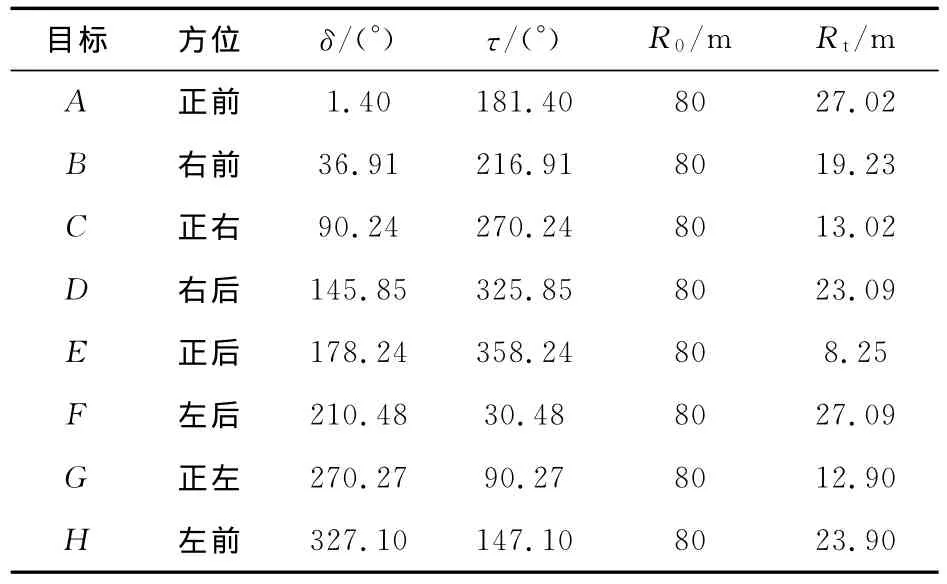
表1 末段修正前后脱靶量统计

3.2 蒙特卡洛法模拟打靶仿真实验

相同条件下，以θ＝45°发射角发射，进行200次蒙特卡洛法模拟打靶仿真试验，首先以无控弹道进行仿真得到平均落点，再以平均落点为目标点，分别进行传统点火相位［4］和文中点火相位的修正仿真，得到3组仿真落点，将其进行对比，如图6、图7，为方便显示，只取其中50组。

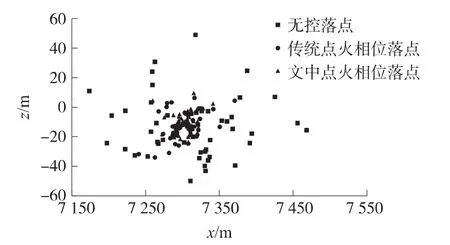
图6 不同点火相位修正后落点散布

显然，无控落点散布较大，采用传统点火相位进行修正后，落点散布有所减小，采用文中点火相位进行修正后落点散布更小。图7为三组仿真落点脱靶量的对比，其中R为脱靶量，n为仿真序号，对于无控模式，传统点火相位和文中点火相位作用下平均脱靶量分别为53.6m，19.9m和13.1m，经过数理统计得到几种模式下的圆概率误差δCEP，如表2所示，表中E为地面密集度。显然，纵向的落点散布比横向的散布大，相比无控弹道落点δCEP，采用传统点火相位修正后δCEP减小42.4%，采用文中点火相位修正后δCEP值为12.4m，减小74.2%，极大地提高了弹丸命中精度和作战效能。

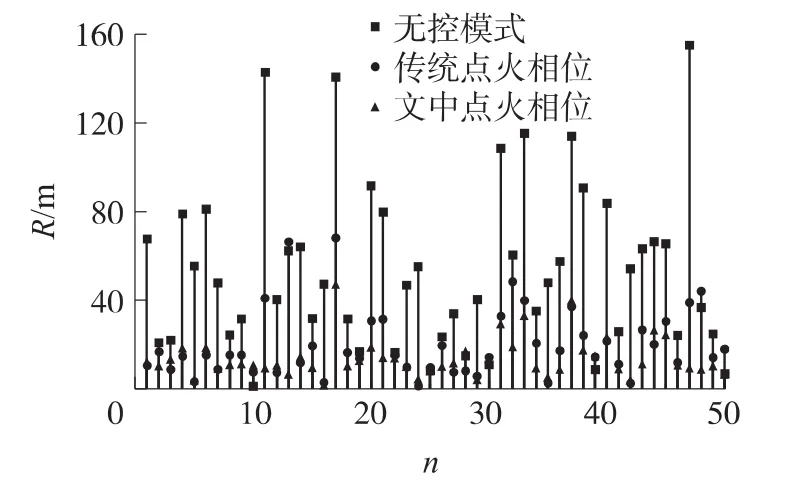
图7 不同点火相位修正后落点脱靶量

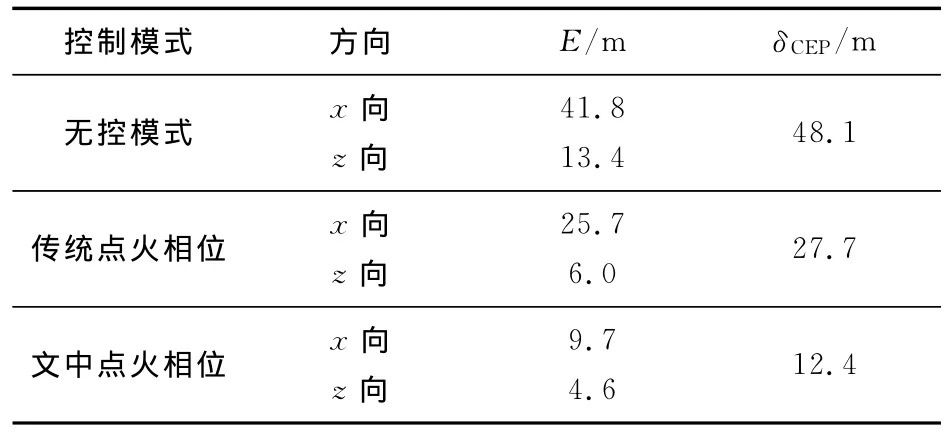
表2 不同点火相位修正效果

4 结束语

以激光半主动末段修正弹为研究对象，研究了经落点预测补偿后得到的目标实际偏差量，结合脉冲力对不同方位的修正能力，得到改进后的脉冲点火相位，通过与无控弹道、传统点火相位修正弹道仿真的对比得知：补偿后的点火相位修正结果δCEP与无控落点相比减小了74.2%，与传统点火相位相比减小了55.2%，且此脉冲点火相位算法不需要过多的传感器，降低了成本，满足高精度低成本弹药的设计准则。

［1］JITPRAPHAL T，BURCHETT B，COSTELLO M.A comparison of different guidance schemes for a direct fire rocket with pulse jet control mechanism［C］／／Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit.Montreal，Canada：AIAA，2001：1－12.

［2］杨荣军，王良明，曹小兵，等.低速滚转末修弹修正量估算方法［J］.弹道学报，2010，22（2）：44－47.YANG Rong－jun，WANG Liang－ming，CAO Xiao－bing，et al.Correction estimation of low－rolling terminal trajectory correc－tion projectile［J］.Journal of Ballistics，2010，22（2）：44－47.（in Chinese）

［3］寇保华，张晓今，杨涛，等.脉冲式末制导子弹导引规律的研究［J］.弹道学报，2005，17（1）：28－31.KOU Bao－hua，ZHANG Xiao－jin，YANG Tao，et al.Study of guidance law for impulse terminal guidance sub－munitions［J］.Journal of Ballistics，2005，17（1）：28－31.（in Chinese）

［4］程振轩，林德福，牟宇，等.探测器指标对制导精度的影响分析［J］.系统仿真学报，2010（9）：2 052－2 055.CHENG Zhen－xuan，LIN De－fu，MU Yu，et al.Analysis of guidance precision due to photo detector index［J］.Journal of System Simulation，2010（9）：2 052－2 055.（in Chinese）

［5］JITPRAPHAI T，COSTELLO M.Dispersion reduction of a direct fire rocket using lateral pulse jets［J］.Journal of Spacecraft and Rockets，2001，38（6）：929－936.

［6］张成.脉冲修正弹药射程预测控制方法［J］.弹道学报，2010，22（1）：20－23.ZHANG Cheng.Range prediction control method for pulse jet correction projectiles［J］.Journal of Ballistics，2010，22（1）：20－23.（in Chinese）

［7］张成，曹营军，杨树兴.一种低速滚转弹药脉冲发动机弹道修正方法［J］.弹道学报，2008，20（2）：45－48.ZHANG Cheng，CAO Ying－jun，YANG Shu－xing.Trajectory correction scheme based on pulse jet for low speed rolling projectile［J］.Journal of Ballistics，2008，20（2）：45－48.（in Chinese）

［8］CALISE A J，EL－SHIRBINY H A.An analysis of aerodynamic control for direct fire spinning projectiles［C］／／Guidance，Navigation and Control Conference.Montreal，Canada：AIAA，2001：1－10.

［9］韩子鹏.弹箭外弹道学［M］.北京理工大学出版社，2008.HAN Zi－peng.Exterior ballistics of projectile and rocket［M］.Beijing：Beijing Institute of Technology Press，2008.（in Chinese）

［10］CORRIVEAU D，BERNER C，FLECK V.Trajectory correction using impulse thrusters for conventional artillery projectiles［C］／／23rd International Symposium on Ballistics.Tarragona，Spain：IBC，2007：639－646.

［11］姚文进，王晓鸣，李文彬，等.末段修正迫弹脉冲发动机控制策略［J］.探测与控制学报，2008，30（S10）：8－10.YAO Wen－jin，WANG Xiao－ming，LI Wen－bin，et al.Control strategy of pulse engine in terminal correction mortar［J］.Journal of Detection ＆ Control，2008，30（S10）：8－ 10.（in Chinese）