关于修订我国炮兵标准气象条件的方法研究

陈文广，李 伟，孙 健

（中国白城兵器试验中心，吉林 白城137001）

目前我国现行的炮兵标准气象条件是借用“苏联”标准，该标准的基础气象数据无论在获取时间上还是地理位置上都与我国实际情况相差甚远，已不适应我国外弹道发展的需要。从上世纪80年代开始，不断有文献提出修订意见［1－3］，但由于以往我国气象探空站点少，积累的气象资料相对匮乏，修订方法一直没有确定，影响了我国火炮实际射击精度，也不满足最大弹道高度的需求。近些年我国探空站进行了整体布局，获取了丰富的30km以下的气象数据，具备了修订我国炮兵标准气象条件所必需的基础数据。

1 我国现行炮兵标准气象条件的局限性

1.1 我国炮兵标准气象条件

我国炮兵标准气象条件分为地面标准值及随高度变化的标准分布规律［3］，标准分布规律将30km以下的大气分成3层，对流层、亚同温层和同温层［2－4］。该标准考虑空气中含有水蒸汽，引入虚温τ的概念，并用它代替气温T［5］。气压采用等温大气模型，即某一气压层的温度假定不随高度变化。而对于30km以上的大气，一般使用国际标准气象条件。目前我国各军兵种还没有统一的标准气象条件，这不利于外弹道设计、气动力计算等方面的理论的严密性和数据的准确性，更不利于多兵种协同作战发展的需要。

1.2 气压模型不符合实际大气

大气气压和温度具有相关性，温度随高度线性递减的大气，称为多元大气。温度的垂直递减率为

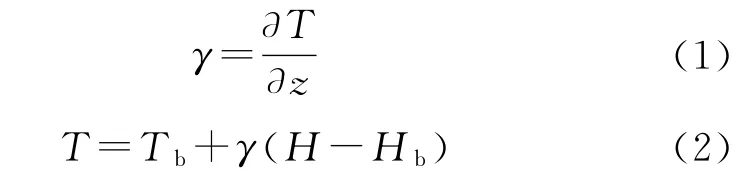
式中：Tb和Hb分别是相应大气层的温度和高度下限值，带下标b的量是与相应大气层下限有关的特性值。在多元大气中，气压随高度变化与温度的垂直递减率有关，温度随高度递减得快，气压随高度递减得也快，令H－Hb＝Hz，依据大气静力学方程和理想气体定律，气压公式为

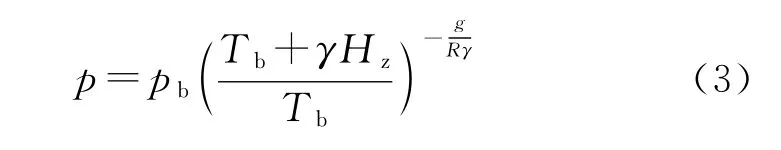
式中：R为空气的气体常数。因气温和气压都是高度的函数，对式（3）的Hz进行求导，可以得到：

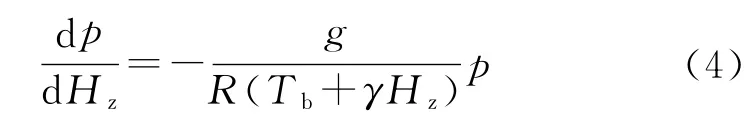
如果当γ＝0时，某一大气层气温不随高度变化，则这一大气层被称为等温大气，假定大气平衡遵循静力学方程，等温大气气压随高度按指数递减，则多元大气压高式（3）简化为等温大气压高公式：

然而，实际大气不存在γ＝0，所以上式中T是上下层温度的平均值。气压是高度的函数，对式（5）的Hz进行求导，可以得到：

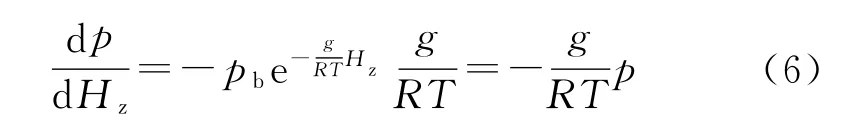
对比式（4）和式（6），变化同样的高度，多元大气模型的气压和等温大气模型的气压变化是不同的，尤其在低空段比较明显。通过对青藏高原高空探测数据统计表明，采用多元大气模型计算结果和实际探测统计结果相差非常小。而气压以100m厚度分层，基点pb随高度的增加而变化，等温大气和多元大气模型下的气压计算结果差别甚至可达100Pa左右。如果pb不变，分层厚度不断增加，气压误差会更大。

1.3 未考虑高空标准风场模型

由《GJB5601－2006中国参考大气》统计表明，我国高空风随高度变化很大，到60km左右的高空，部分地区风速可达到90m／s，而我国现用炮兵标准气象条件规定风速为0。这对于精度要求很高的常规远程弹箭来说，若假定高空平均风速为0，将会导致较大的修正误差，这有违人们建立标准大气的初衷［6］。

2 有关修订我国炮兵标准气象条件的研究现状

关于修订我国炮兵标准气象条件方案的文献很多，李臣明等建议在30km以下仍然采用原炮兵标准气象条件，30km以上采用国际标准气象条件［7］；王军波等建议把现用炮兵标准气象条件的温度解析函数第一拐点设在16km，第二拐点设在19km［3］；王中原等分析并建议了建立我国炮兵高空标准气象条件的方法［8］；赵建斌论证了高空气象条件及其对弹箭弹道特性的影响分析［9］。以上所有的论证或研究仅仅是关于某一区域气象条件的论述，还没有系统研究全国气象要素随高度的变化规律，而且大部分是引用标准，统计实测数据少，温度解析函数拐点选择混乱，对流层顶高度变化的地域或季节特点没有被考虑，气压仍然沿用等温大气模型，和实际大气差异较大。

基于我国现行炮兵标准气象条件的局限性及有关单位对其修订的研究现状，本文提出了以下修订方法并进行了应用验证。

3 我国炮兵标准气象条件的修订方法

3.1 区域及站点的选择

我国南北跨纬度近50°、东西跨经度60°以上。南北温差季节明显、东西海拔高度差大。根据中国国家地理可以把中国分为北方、南方、西北和青藏4大区域，每个区域的气候影响因素都不一样。在我国地域内制定单一炮兵标准气象条件，不利于实际射击、外弹道研究和射表编拟的需要，为了各个军兵种联合作战，以及弹箭飞行特性比较需要，需要制定出统一的、具有地域代表性的标准气象条件，所以应根据我国多样化需求修订炮兵标准气象条件。

目前我国共有地面气象观测站2 500个左右，高空气象探测站124个左右，东部密集，西部稀疏，疏密相差悬殊。因此，必须考虑各个气象站代表面积的“权重”问题，尤其是研究青藏高原炮兵标准气象条件的时候，高空气象探测站仅有26个，地面站却多达156个，站点从海拔高度1km到4km以上都有分布。那么，在修订炮兵标准气象条件时，地面气象观测站选择要合理，否则地面与高空气象探测站的数据对接时，绘制的数据曲线可能出现不规则形状，无法正确反映实际气象条件变化规律。

3.2 地面标准值的计算

由于近地面层气温的日变化较大，需要在固定时间多次测量取平均值才具有代表性。目前我国气象台站一日进行24时次或4时次（8、14、20、2时）观测地面气温。用地面平均气温来代替高空探测（12、24时）的地面气温的平均值，可以避免采用两次高空探测的地面温度给求取温度垂直递减率带来偏差。

各地面气象观测站点海拔高度不同，为了便于统计和比较，通常是把各站的地面气温、气压修正到某一位势高度上的气温和气压。考虑海拔高度变化对气温存在影响，对不同的气象站修正时选取同一温度垂直递减率［1］，其递减率可以先选择6.328×10－3，经过数据统计后，计算出统计地域的温度垂直递减率，再进行回归统计，就会得到比较准确的地面值。

以往的研究都是依据大气静力平衡条件下的压高公式，把各气象探测站的地面气压值修正为海平面气压［1－5］。而我国东西海拔高度差大，如果把青藏高原气压修正到海平面气压，不考虑温度垂直递减率的变化，必定会带来较大的误差。所以，地面标准气象条件的制定不一定非要修订到同一海平面，可以根据实际需要，修订到某一海拔高度的地面值。

3.3 温度解析函数拐点的选择

大部分文献都说明了原苏联炮兵标准气象条件中对流层顶高度不符合我国实际气候环境。仍以青藏高原为例，统计资料表明，其对流层顶高度在夏季时高，冬季低，夏季在17km左右，冬季存在双对流层顶现象，第一对流层顶在12km左右，第二对流层顶在17km左右［10］，根据累年实际温度统计的结果，在12～20km高空形成一个过渡带，所以在研究30km以下的青藏高原炮兵标准气象条件时，温度曲线拟合拐点应该分别设定在12km和20km左右是比较合理的。

3.4 气压模型的选择

文献［11］论证了由计算气压偏差而产生的射击诸元误差是不容忽视的。前文已经说明了采用等温大气模型所带来的误差，尤其在低空段等温大气模型计算的气压和实际统计结果差异比较大，所以炮兵标准气象条件应采用多元大气模型，不仅要考虑温度的垂直变化率，还要考虑气压基点的变化，弱化温度和气压的相关性，由低向高逐层计算求得气压。

3.5 虚温代替温度

我国现用炮兵标准气象条件假定空气是不干洁的，国际上通用的标准大气，假定空气是干洁的，所以用虚温代替温度存在一些争议。文献［5］建议我国采用国际通用大气标准，而由实际探空资料表明虚温订正值近地面一般最大，随着高度增加而减小，同时也有文献［11］研究证明在高温、高湿的季节，湿度对射击诸元的精度影响是比较大的，那么在修订我国炮兵标准气象条件时，尤其在近地面虚温订正值不能忽略，仍要采用虚温代替温度。

3.6 高空标准风场模型的统计方法

风向、风速是对风的一种描述，是具有相关性的同一体，不可分别独立统计。应根据风向，把风分解成2个互相垂直的分量，对这两个分量分别进行单独统计。统计完成后再合成风速，计算出风向。

以我国海拔高度在1～3km的喀什、和田、芒崖等十几个高空探测站为例，对它们2008年～2012年的L波段雷达的探空数据进行累年历月统计，结果如图1和图2所示。图中绘出了高度2～30km的风向D、风速vw的变化曲线，每一条曲线代表一个月份，共12个月。可以看出，风向风速在离开地面几km后，呈现有规律的变化。风的形成和风速大小、温度梯度密切相关，影响因素多，因果关系复杂，很难从理论研究方面确立风场分布的数学模型，而采用统计学方法，对探测的不同时间、地域的气象资料进行归纳分析，可以获得风场数学模型。

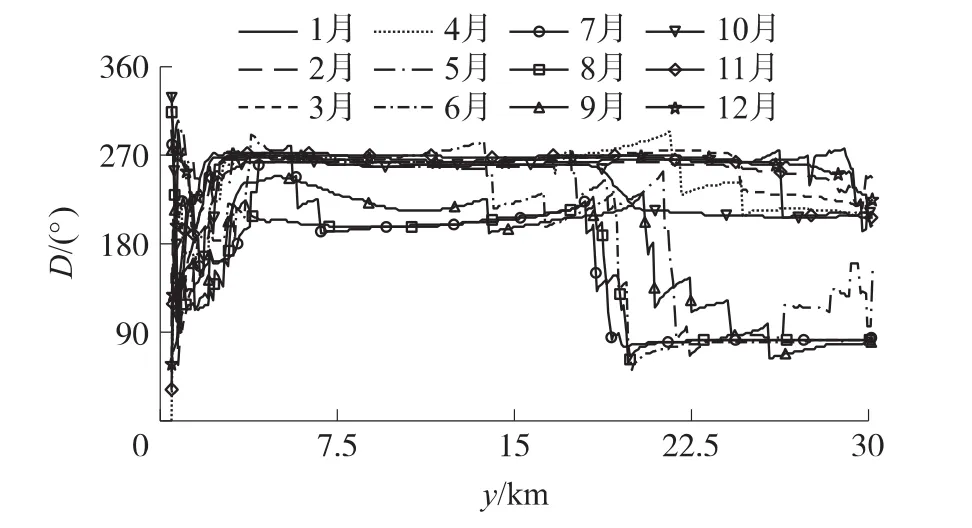
图1 风向随高度变化图

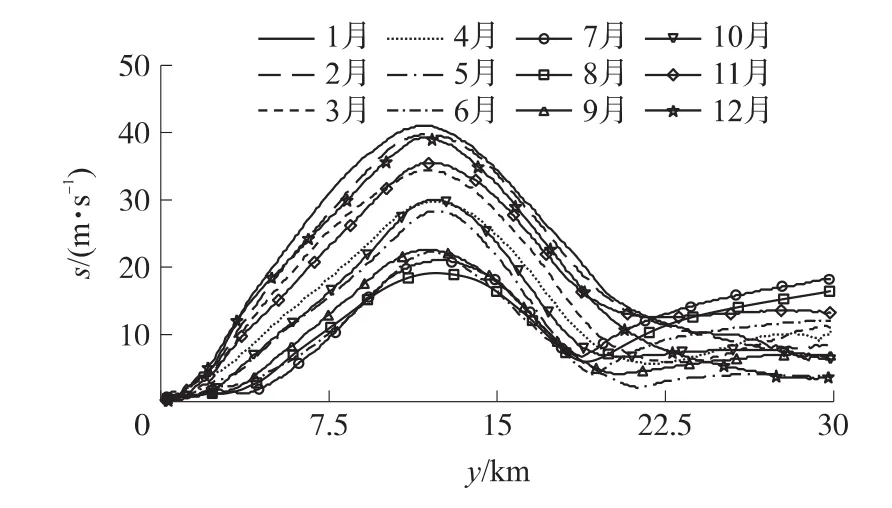
图2 风速随高度变化图

3.7 30～80km数据获取方法

《GJB366.1－87航空与航天用参考大气》和《GJB5601－2006中国参考大气》都统计了我国80km以下大气特性参数随纬度和季节的变化规律，但是用于炮兵标准气象条件计算还是过于粗糙。我国在30～80km高度内温度、湿度、气压、风和空气密度的探空数据比较少，可供参考的有卫星探测数据、中国靶场参考大气、北半球标准大气、美国标准大气、苏联标准大气。对30～80km炮兵标准气象条件制定，参考这些资料同时也要收集我国探空火箭和下投式探空仪的数据。虽然参考数据少，但是30km以上的大气趋于平稳，具有一定的规律性，可以以一定模型进行高度外推，求取30km以上气象要素变化规律。

3.8 数据处理与对接方法

对于温度、湿度、气压、风、空气密度等要素，在相同的位势高度上，采用历年月统计、历年年统计、累年月统计、累年年统计等多种统计方法，按高度绘制变化曲线，进行趋势的分析及比较。对于统计结果的分布规律研究，可以通过函数逼近的方法来解决。根据求取的温度、湿度、气压、风和空气密度的平均数据，作为绘图数据样本点，基于绘图曲线判断出曲线拐点，通过最小二乘法等拟合方法，就可以拟合到有效的解析函数。

以目前的数据来看，地面到30km左右高度为实测数据，而且数据量多，而30km以上的数据多为反演、平滑和内插的数据。所以要保证在30km附近炮兵标准气象条件中的两种不同数据平滑连续，就要在20～30km形成过渡带。根据经验，采用线性变化或加权平均等方法，可以使气象要素曲线连续平滑。

4 修订方法应用

4.1 说明

由于篇幅限制，本文仅以30km以下大气层的高原气象资料为例，应用以上方法，以海拔高度1～3km，3～5km为起始点，统计了高原温度的变化规律。气压采用多元大气模型，其温度垂直递减率采用统计的温度随高度变化规律的一次项系数近似求得。

4.2 地面海拔高度1～3km的气象要素变化规律

1）地面值。τ＝19.42℃，pon＝794.09hPa，τ＝292.57K，ρon＝978.551g／m3，无风。

2）温度τ随海拔高度y（地面海拔高度1km以上）的分布规律。

当y≤11.8km时，有：

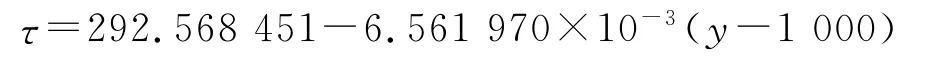
当11.8km≤y≤22km时，有：

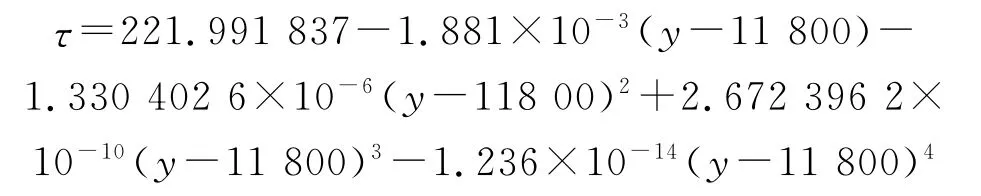
当22km≤y≤30km时，有：

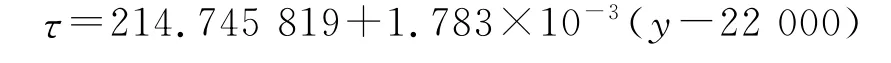
4.3 地面海拔高度3～5km的气象要素变化规律

1）地面值。τ＝9.72℃，pon＝641.84hPa，τ＝282.87K，ρon＝813.0g／m3，无风。

2）温度τ随海拔高度y（地面海拔高度3km以上）的分布规律。

当y≤11.8km时，有：

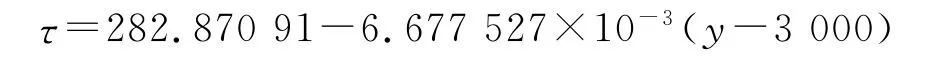
当11.8km≤y≤22km时，有：

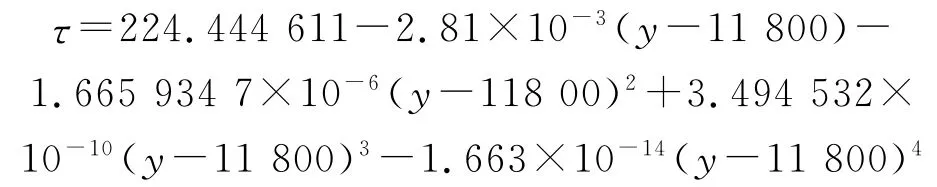
当22km≤y≤30km时，有：

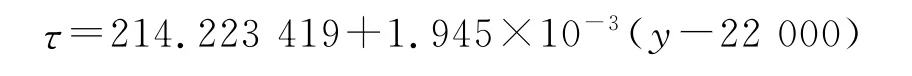
5 结论

将某研究所以青藏高原标准层和特性层气象资料为样本而统计的温度变化规律、前苏联炮兵标准气象条件、实际统计温度变化规律和本文拟合的温度变化规律进行对比分析，如图3和图4所示。

从图可以看出，通过本文提出的修订方法得出的温度变化曲线不仅平滑，与我国高原实际统计的温度变化规律基本一致，也与某研究所统计的最新高原气象要素变化规律有较高相似度，所以本文提出的修订方法更具有科学性。由于气压和温度具有相关性，通过多元大气模型，以及温度垂直递减率即可计算气压变化规律，在此不再赘述。

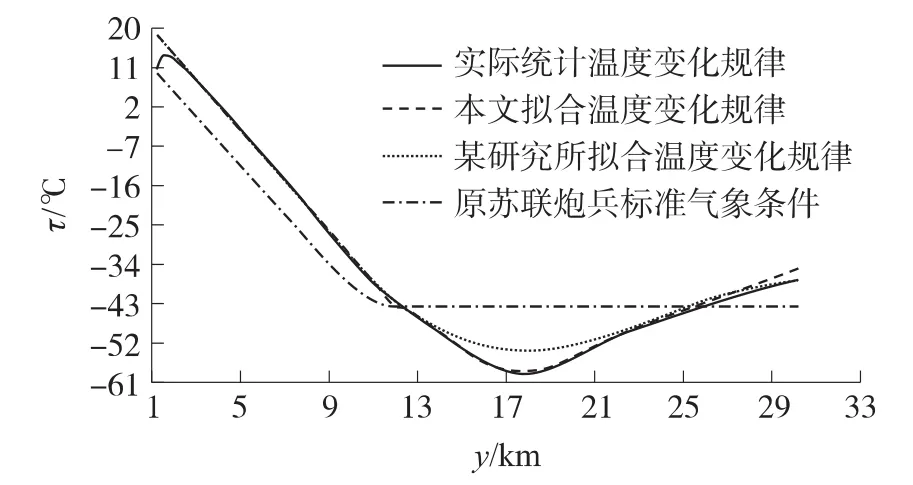
图3 地面海拔高度1～3km温度变化对比分析图

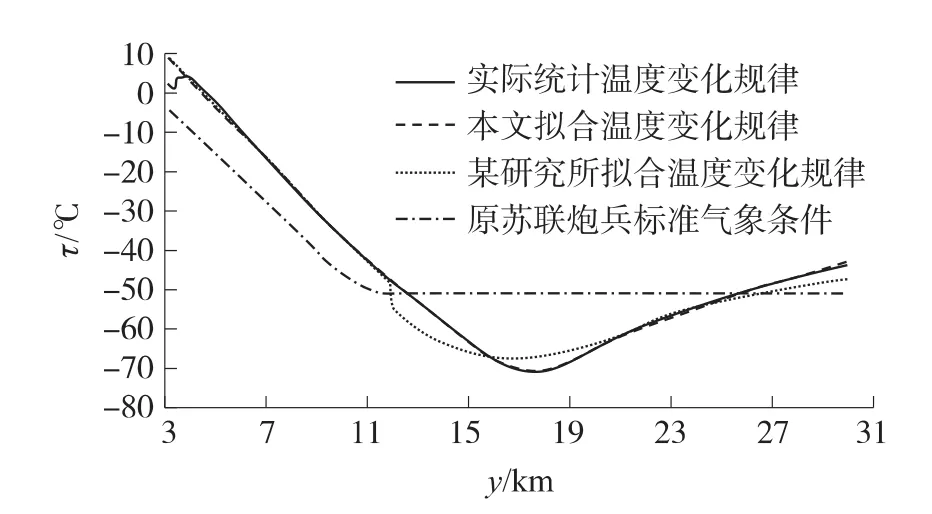
图4 地面海拔高度3～5km温度变化对比分析图

［1］王玉昆.关于我国各军兵种标准气象条件方案的建议［J］.兵工学报弹箭分册，1982，（2）：28－35.WANG Yu－kun.On the arms of standard meteorological conditions of our suggestion scheme［J］.Journal of China Ordnance Projectiles Fascicle，1982，（2）：28－35.（in Chinese）

［2］刘玉文，陈春，姚若河.军用气象条件亟待改进的若干问题的商榷［J］.气象科学，2005，25（1）：55－58.LIU Yu－wen，CHEN Chun，YAO Ruo－he.Discussion of problems concerning military meteorologic conditions［J］.Scientia Meteorologica Sinica，2005，25（1）：55－58.（in Chinese）

［3］王军波，张军挪，涂胜元.修订我国炮兵标准气象条件的必要性及方法［J］.华北工学院学报，2005，26（3）：174－176.WANG Jun－bo，ZHANG Jun－nuo，TU Sheng－yuan.Necessary and method on revising of artillery stardard atmospheric conditions of our country［J］.Journal of North China Institute of Technology，2005，26（3）：174－176.（in Chinese）

［4］徐明友.火箭外弹道学［M］.北京：国防工业出版社，1986.XU Ming－you.Exterior ballistics of rocket［M］.Beijing：National Defense Industry Press，1986.（in Chinese）

［5］张峰.标准气象条件使用中存在的问题［J］.弹道学报，1999，11（4）：78－81.ZHANG Feng.The problems in use standard atmosphere［J］.Journal of ballistics，1999，11（4）：78－81.（in Chinese）

［6］李臣明.高空气象与气动力对远程弹箭弹道影响的研究［D］.南京：南京理工大学，2007：44－45.LI Chen－ming.Study on ballistic influence of meteorology and aerodynamic force for long－range shells and rockets under high altitude［D］.Nanjing：Nanjing University of Science and Technology，2007：44－45.（in Chinese）

［7］李臣明，朱国权，韩子鹏.不同标准大气对远程弹箭射程影响的计算分析［J］.弹箭与制导学报，2006，26（2）：150－152.LI Chen－ming，ZHU Guo－quan，HAN Zi－peng.The calculation and analysis to long－range shell－rocket using different standard atmospheres ［J］.Journal of Missiles and Guidance，2006，26（2）：150－152.（in Chinese）

［8］王中原，韩子鹏，林献武.对建立我国炮兵高空标准气象条件的分析和建议［J］.弹道学报，2007，19（1）：9－11.WANG Zhong－yuan，HAN Zi－peng，LIN Xian－wu.Analysis and suggestion of standard atmospheric condition at super－altitude for Chinese artillery ［J］.Journal of Ballistics，2007，19（1）：9－11.（in Chinese）

［9］赵建斌，翟英存，刘明喜.高空气象条件及其对弹箭弹道特性的影响分析［J］.弹箭与制导学报，2008，28（1）：177－180.ZHAO Jian－bin，ZHAI Ying－cun，LIU Ming－xi.The analysis of upper air weather condition and its influence on trajectory characteristic of the missile and rocket［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2008，28（1）：177－180.（in Chinese）

［10］李鹏.青藏高原大气臭氧与对流层顶的关系［D］.北京：中国科学院研究生院（大气物理研究所），2007：14－20.LI Peng.Ozone and tropopause over the Tibet plateau relationship［D］.Beijing：Graduate University of Chinese Academy of Sciences（Research Institute of Atmospheric Physics），2007：14－20.（in Chinese）

［11］王兆胜.远程炮武器系统射击精度研究与射击精度战技指标论证［D］.南京：南京理工大学，2003：36－37.WANG Zhao－sheng.The study of firing accuracy and firing accuracy tactical＆technical requirement reasoning for long range gunnery system［D］.Nanjing：Nanjing University of Science and Technology，2003：36－37.（in Chinese）