脉冲修正火箭弹弹道修正算法优化

李超旺，高 敏，宋卫东，郭庆伟

（军械工程学院1.导弹工程系；2.火炮工程系，石家庄050003）

脉冲推冲器具有结构简单、响应时间短和能快速修正弹丸飞行轨迹的特点，是弹道修正弹常用的一种执行机构。脉冲推冲器的修正能力有限，当脉冲推冲器的个数和冲量一定时，点火控制优化是提高弹道修正弹作战效能的有效途径［1－2］。

当前，脉冲推冲器的点火控制主要围绕末段弹道修正展开［1－3］，当无控弹箭的落点散布较大时，仅在末段进行弹道修正无法满足精度要求。是否可将末段修正点火控制方法直接扩展到其它弹道阶段上还没有相关的论述。末制导的点火控制是以多级脉冲推冲器作为控制对象［1］，根据稳定性的要求，脉冲推冲器激活需要设置一定的时间间隔，激活时间间隔较大时末制导点火控制方法会产生较大的剩余误差。为了提高弹道修正弹的修正效能，需要对中制导的点火条件进行研究。

首先，建立了脉冲修正火箭弹的飞行控制模型，在此基础上对脉冲推冲器弹道修正特点进行分析，根据脉冲推冲器在不同方向弹道修正能力分布特点提出了一种中制导的点火策略，针对卫星制导的特点，优化了点火相位，为验证所提控制策略和点火相位的正确性，采用蒙特卡洛模拟打靶对弹道修正优化算法进行了数值计算，并对计算结果进行了分析。

1 脉冲修正弹飞行控制模型

弹道修正舱的执行机构由许多独立的脉冲推冲器组成，其安装轴线与火箭弹对称轴垂直，如图1所示。

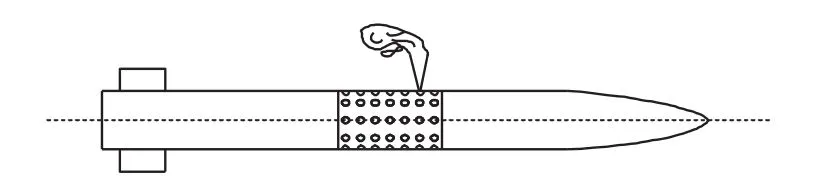
图1 脉冲推冲器径向布置图

飞行过程中，脉冲推冲器随弹体一起低速旋转，在空间的某一时刻、特定方位点火后能为弹道修正提供控制力或力矩，如图2所示，改变弹体的速度或姿态，修正弹道轨迹。图中，F为脉冲推冲器作用时提供的推力，Fy、Fz为脉冲力在准弹体坐标系y轴和z轴上的分量，γ为点火相位角，ωx为脉冲推冲器工作时弹体的旋转速度。

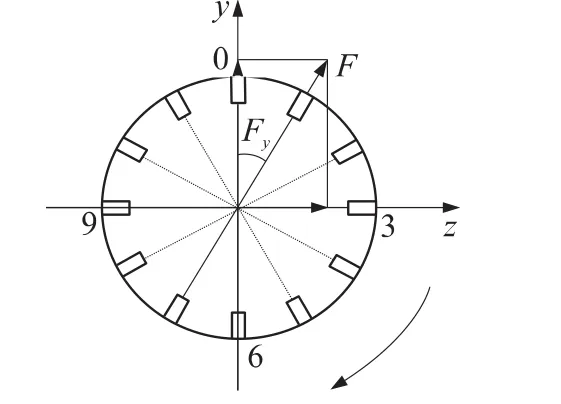
图2 脉冲发动机径向推力示意图

假设脉冲推冲器为c圈，每圈n（为分析方便，设n为偶数）个，则同圈相邻2个脉冲推冲器方位夹角为2π／n。

假设点火时刻第i（1≤i≤n）个脉冲推冲器对应的点火滚转角为γi，则第i个脉冲推冲器作用时平均控制力的大小和方向为

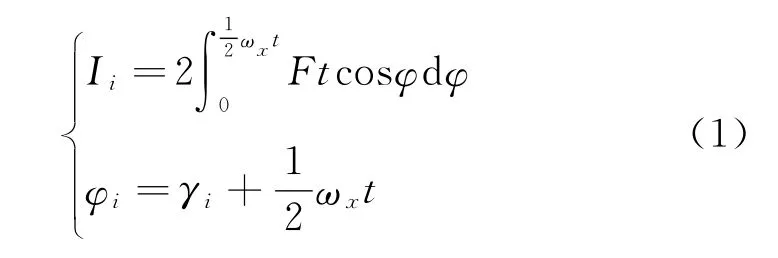
由牛顿第二定律知，第i个脉冲推冲器作用后在准弹体坐标系内产生的速度增量为

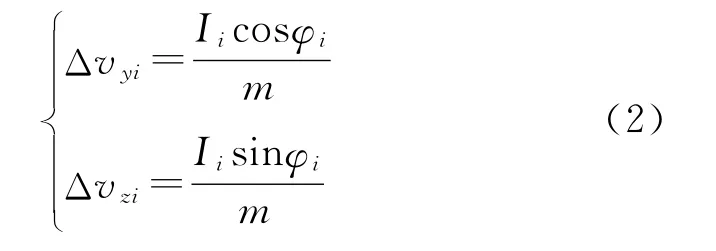
式中：m为弹体的质量。

在此过程中产生的位移变化量为

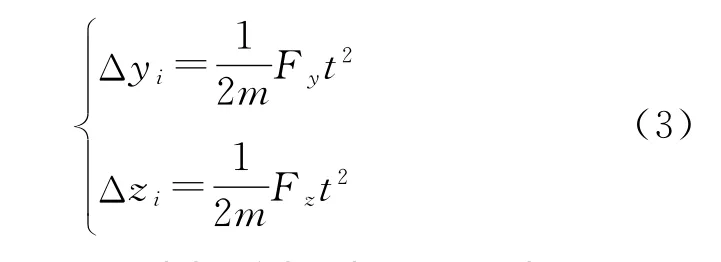
假设火箭弹主发动机关机以后质量为45kg，脉冲推冲器点火持续时间为20ms，推力为1 200N，由式（3）得脉冲作用产生的极值位移量为cm级，完全可以忽略。脉冲推冲器对于弹道的修正主要是改变弹体的速度，通过时间的积累达到修正弹道的目的。仿真解算时将式（2）引入到弹道方程，提供控制力。

2 点火条件分析与优化

2.1 点火条件分析

点火条件包括确定脉冲推冲器的点火时间、选择点火阈值和点火相位等［3］。点火条件主要与脉冲推冲器的冲量（大小、持续时间）和修正方式有关系，为了优化点火条件，不仅要对脉冲推冲器的修正能力进行分析，还要对不同的修正方式进行研究。

脉冲修正能力主要与脉冲推冲器点火时间、点火相位和射角有关系［4］。对于某一弹道来说，其射角是一定的，脉冲修正能力取决于点火时间和点火相位。

修正方式按制导时段分为中制导和末制导。末制导作用距离较短，集中在1～2km内，一般采用“一次预测，多次修正，闭合控制”的控制方法［1，4］，当修正弹落点偏差较小时，采用该方法是合适的，但当落点偏差较大、脉冲点火时间间隔较长时，采用该方法会产生较大的方法误差。中制导一般采用卫星制导或者惯性导航，一旦定位成功便可对弹体的飞行轨迹进行控制，可控制的弹道段大幅增加，与末制导相比，脉冲推冲器的作用范围扩大。假设2个脉冲推冲器相继点火的时间间隔不小于0.3s，卫星导航信号的刷新周期不大于0.1s，并且落点预测算法具有实时性和收敛性，则可以采用“多次预测，多次修正，闭环控制”的方法对每一个脉冲推冲器单独进行控制，在减小剩余误差的同时扩大了修正弹的修正范围。

2.2 点火条件优化

由方程（2）可知，对于质量为m的弹体，第i个脉冲作用后弹体法向速度增量为Δvyi，横向速度增量为Δvzi。Δvzi对于横向修正距离的贡献与剩余飞行时间有关。对于某一固定弹道，修正时间越早则剩余飞行时间越长，横向修正距离将越大。

纵向修正相对复杂，脉冲推冲器对纵向的修正如图3所示，在上升段，脉冲力作用后，增加了法向速度，但同时减小了纵向速度。法向速度增量Δvzi延长了火箭弹的留空时间，这一延长留空时间引起的纵向修正距离和纵向速度有关，纵向速度越大修正距离越大，反之，则修正距离小。同时，脉冲作用引起的纵向速度减小量缩短了弹体的飞行距离，抵消了部分修正能力。在弹道的下降段，法向速度增量和纵向速度改变对于距离的修正是同方向的，原因分析可以采用上升段的方式。

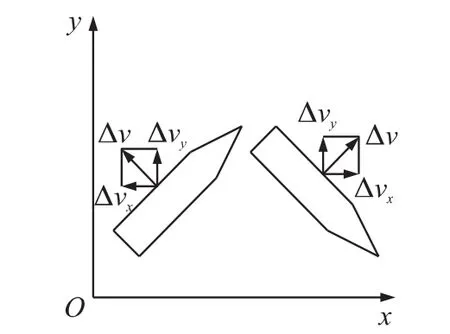
图3 脉冲修正示意图

选取的脉冲性能参数：单个脉冲推冲器的冲量15N·s，持续时间16ms。设点火方位0°角与准弹体系的y轴重合，从弹尾向弹头方向看，点火方位角顺时针增大。

以122mm火箭弹为例，建立了六自由度弹道方程［5－6］，以火箭弹质心处的某一脉冲推冲器作为控制对象，以点火时间和点火角度为自变量，在标准气象且45°射角条件下，仿真解算了脉冲推冲器在全弹道的修正能力的变化情况。仿真结果显示，火箭弹在41.65s左右到达弹道顶点。飞行过程中弹体转速变化情况如图4所示。

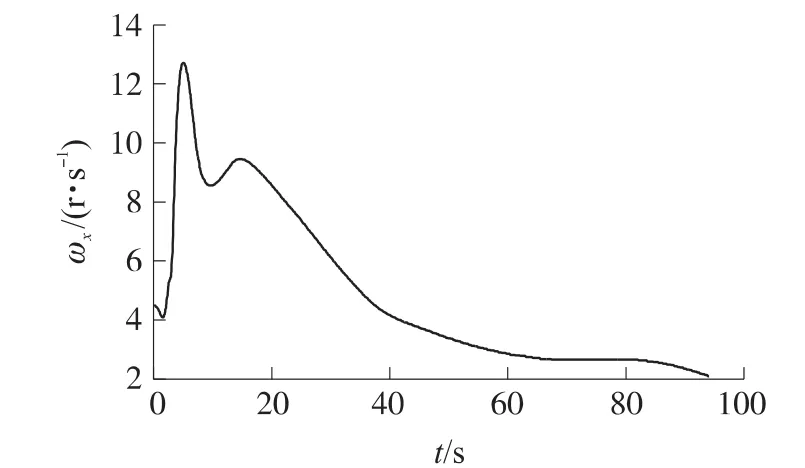
图4 火箭弹转速随飞行时间的变化

从图4可以看出，弹体转速范围为2～12.8r／s，受导转力矩的影响，发动机熄火之前弹体转速一直在升高，发动机关机时弹体转速达到最高，约12.8r／s，受滚转阻尼力矩的影响，发动机关机以后弹体滚转速度逐渐减低，60s左右导转力矩和滚转阻尼力矩达到一个平衡，此时转速约为3r／s。

仿真解算的单个脉冲推冲器修正能力与点火时间、点火方位的关系见表1。表中，t为飞行时间，ΔL和ΔH分别为脉冲推冲器在纵向和横向上的弹道修正能力。根据表1绘制修正能力图，如图5所示。

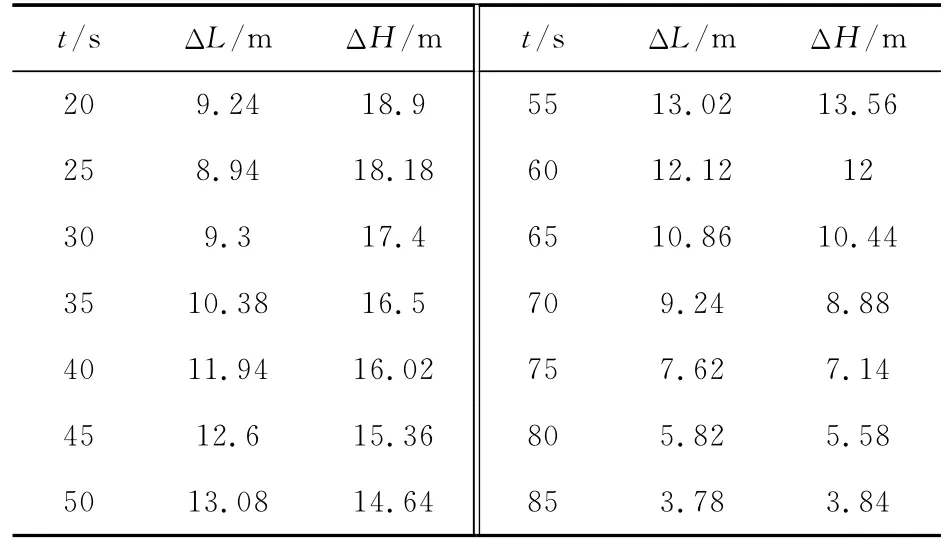
表1 弹道修正能力与点火时间对应关系表

从表1和图5可以看出，横向修正能力随着时间的推移逐渐降低，与上面的理论分析一致。以弹道顶点为分界点，弹道顶点之后横向修正能力衰减的速度较弹道顶点之前快。由图4可知，火箭弹到达顶点之前，弹体转速较高，脉冲推冲器作用过程扫过的角度会较大，由式（1）、式（2）可知，作用力对速度的改变量将减小，而到达弹道顶点以后，转速小且稳定，此时修正能力基本上只与剩余时间有关系。

从表1和图5还可以看出，在上升段，纵向修正能力远小于横向修正能力，下降段时，纵向修正能力与横向修正能力基本相当。在上升段，随着时间的推移纵向修正能力在不断的增加，在弹道顶点附近修正能力达到最大。此后随着时间的推移修正能力不断降低，仿真解算结果验证了上面的理论分析。

从以上理论分析和数据结果可知：脉冲推冲器横向修正能力随着时间的推移而递减，纵向修正能力在上升段不断增强，在弹道顶点处达到最大，此后修正能力逐渐衰减。脉冲推冲器在上升段的横向修正能力远大于纵向修正能力，而下降段的横向、纵向修正能力相当，基于此，确定火箭弹脉冲修正策略为上升段，只进行横向修正，过弹道顶点以后进行综合修正。

工程应用中将表1计算的时间－脉冲修正能力对应表装定到飞行控制软件中，飞行中利用查表插值法实时解算脉冲推冲器的修正能力，当预测偏差同时大于点火阈值和脉冲修正能力时，激活脉冲推冲器。

上升段只进行横向修正，当横向偏差为正时，说明预测落点在目标点的右边，控制力应指向横偏的负向，对应的点火方位为90°，反之，当横向偏差为负时，点火方位应为270°。下降段进行综合修正，点火方位相对复杂，为了分析方便，以目标点为原点建立了目标点坐标系，如图6所示，其中O点为目标点，Ox轴与炮目连线重合，射程增加方向为正，Oz轴为横偏方向，垂直于Ox轴，Ox轴绕目标点顺时针旋转90°为Oz的正方向。

设T为预测的弹道落点，则Δx和Δz分别为预测偏差纵向、横向分量。当横向、纵向修正距离和横向、纵向修正力成同比增长时，沿OT方向进行点火，脉冲推冲器在横向和纵向的修正距离比值将等于预测偏差横向和纵向分量比值，即：

此时剩余偏差最小，为AT。而由表1和图5发现，对于同一弹道点，当作用力相等时横向和纵向的修正距离并不相等，即横向、纵向修正距离和修正力不是同比增长关系。沿OT方向进行点火，假设产生的纵向和横向偏差分别为ΔL、ΔH，则剩余弹道偏差为BT。由三角形的性质可知BT＞AT，此时剩余偏差大于最小剩余偏差。为了减小剩余误差，需要对点火相位进行优化。相位优化的目标是确保：

假设优化后的点火相位为φ，则纵向、横向分力为

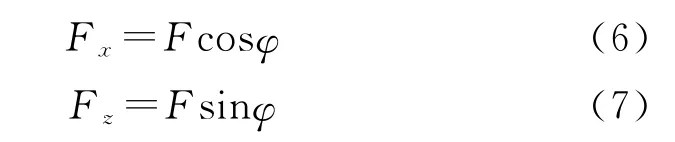
由表1可得，同样的作用力在相同的时间点对于横向、纵向的修正能力不同，设这一比值为k，则由式（6）和式（7）可得同一时间点脉冲推冲器在横向、纵向的修正距离比值为

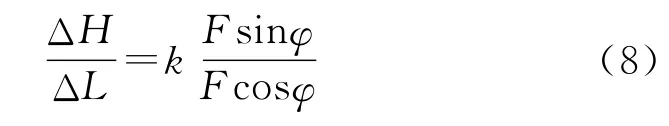
当点火相位最优时满足：

即：

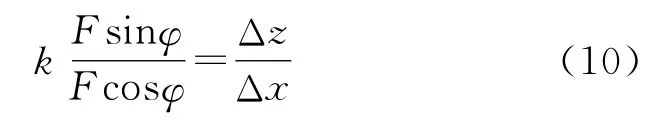
则由式（8）～式（10）可得：

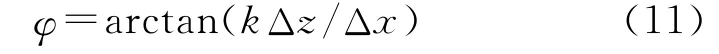
沿此方位角激活脉冲推冲器，剩余误差最小，此点火方位角为最优点火方位角。工程应用中可将修正能力比值提前解算出来，存储到飞行控制软件中，飞行中根据需要实时进行查表插值解算。

3 数值计算及结果分析

以具有6圈、每圈8个脉冲推冲器的弹道修正火箭弹为例，以45°射角对应弹道的落点为目标点，相应的目标射程为32 009m，在随机干扰条件下对无控弹和修正弹各进行了100次模拟打靶数值计算。计算中风速的误差均值为3m／s，密度的误差均值为0.2kg／m3，温度误差均值为2℃，气动系数误差均值：滚转力矩系数误差均值为0.1，升力系数误差均值为0.15，法向力系数误差均值为0.05，阻力系数误差均值为0.15，压心系数误差均值为0.02。

火箭弹的总体参数见表2所示。表中m为火箭弹质量，J为极转动惯量，Jc为赤道转动惯量，l为质心距弹顶的距离，d为弹体直径。脉冲推冲器的冲量为15N·s，最大推力为2 400N，作用时间为20ms。

表2 火箭弹总体参数

在验证控制算法有效性之前，首先仿真分析了采用脉冲推冲器进行弹道修正时火箭弹的飞行稳定性，某一弹道最大的攻角α与飞行时间的对比关系如图7所示。

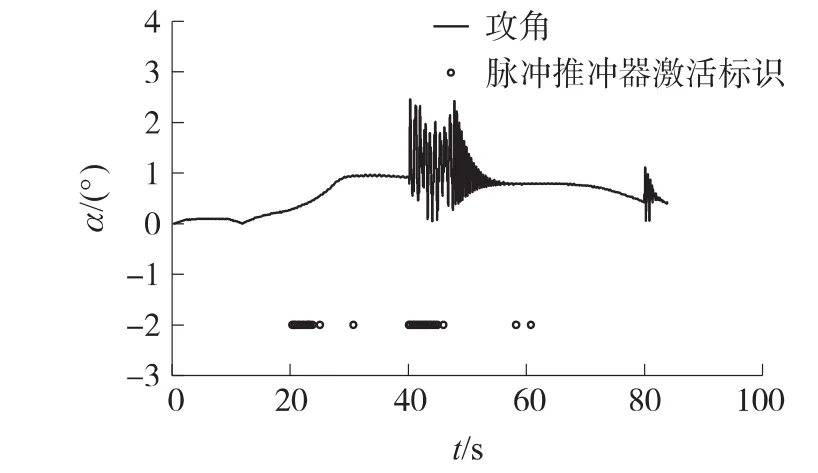
图7 脉冲推冲器修正时攻角－时间对比关系图

从图7中可以看出，脉冲推冲器从20s开始进行弹道修正，此时由于速度较大，弹体只是产生了实现弹道修正所需的攻角，并没有出现振动现象。40s左右到达弹道顶点，从脉冲推冲器点火标识可以看出，在40s后持续激活了多个脉冲推冲器，由于此时火箭弹速度较小，每次脉冲修正都引起了弹体的大幅度摆动，最大攻角为2.5°左右，47s左右脉冲推冲器停止对弹道的修正，弹体在静态稳定力矩的作用下攻角将逐渐减小。在整个的飞行过程中弹体攻角一直小于3°的要求范围［6］，满足飞行稳定性的要求。

1）仿真试验1。 采用末制导点火控制算法进行弹道控制仿真试验，试验中在弹道的上升段火箭弹进行无控飞行，下降段进行综合修正，其中点火相位为

无控弹落点和采用末制导点火控制方法修正后的弹着点的落点散布如图8所示。图中（0，0）为目标点，Δx和Δz分别为实际落点与目标点之间的纵向、横向偏差。Δx为正时表示实际落点比目标点远，反之则近；Δz为正时，表示实际落点在目标点的右侧，反之在左侧。

从图8可以看出，采用末制导点火控制算法对弹道修正火箭弹进行控制修正后，火箭弹的射击密集度明显得到提高，但是，由于末制导点火控制只在弹道的末端对弹道进行控制，没有对点火相位进行优化，修正能力严重不足，这导致剩余误差较大，表现为较多的弹着点距目标点（0，0）的距离较大，由图8可见。经统计可知，无控弹圆概率误差（CEP）为680.3m，修正后CEP为119.7m，射击精度无法满足精确打击要求。

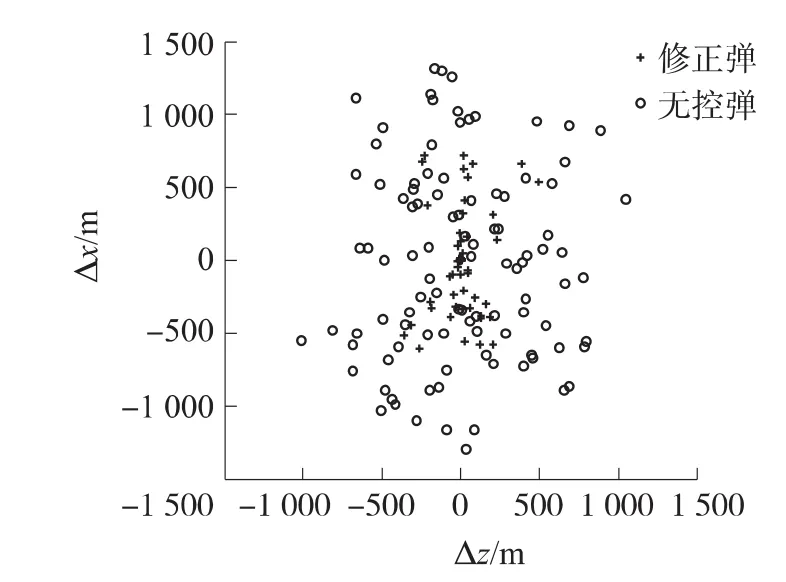
图8 末制导控制修正弹和无控弹落点散布图

2）仿真试验2。 采用优化后的算法对点火控制进行了仿真试验，在弹道的上升段开始进行横向修正，进入下降段以后进行综合修正，点火相位由式（11）计算得出。无控弹落点和控制算法优化后的修正弹弹着点落点分布如图9所示。

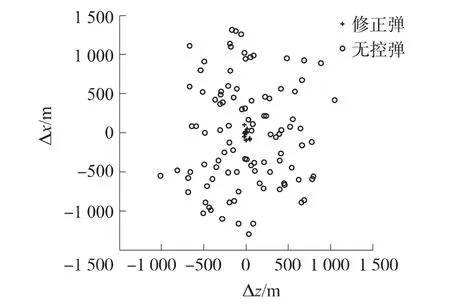
图9 控制算法优化后修正弹和无控弹落点散布图

从图9可以看出，对脉冲推冲器点火控制进行优化后，弹道修正火箭弹的修正能力得到了较大提高，可以满足落点散布对于修正能力的需求。火箭弹经弹道修正后，弹着点与目标点的距离都能控制在100m以内，绝大多数集中在30m以内，与末制导点火控制相比，弹道修正火箭弹射击密集度和精度都得到明显提高，经统计，优化算法后弹道修正火箭弹的圆概率误差（CEP）提高到19.8m。

4 结束语

脉冲推冲器是弹道修正弹常用的一种执行机构，其修正算法直接影响到弹道修正效果。在建立火箭弹控制模型的基础上对脉冲推冲器的修正能力进行了计算，针对同一脉冲推冲器对于不同方向的修正能力不同，从点火时机和点火相位着手对点火控制方法进行了优化，扩大了脉冲推冲器的使用范围，提高了火箭弹的修正能力。采用传统的末制导点火控制方法和优化后的点火控制方法对122mm弹道修正火箭弹分别进行了仿真试验，试验结果表明，采用传统的点火控制方法后火箭弹的CEP从680.3m提高到了119.7m，而点火控制算法经优化后这一CEP达到了19.8m，弹道修正弹射击精度明显得到提高。

［1］JITPRAPHAI T，COSTELLO M.Dispersion reduction of a direct fire rocket using lateral pulse jets［J］.Journal of Spacecraft and Rockets，2001，38（6）：929－936.

［2］曹营军，杨树兴.基于脉冲控制的末段弹道修正弹点火相位优化研究［J］.兵工学报，2008，29（8）：897－901.CAO Ying－jun，YANG Shu－xing.Research on firing phase angle optimization of terminal trajectory correction projectile based on pulse jet control ［J］.Acta Armamentarii，2008，29（8）：897－901.（in Chinese）

［3］杨红伟，窦丽华.防空弹道修正弹脉冲执行机构的控制方法［J］.北京理工大学学报，2011，31（10）：1 184－1 188.YANG Hong－wei，DOU Li－hua.Control method of impulse actuator of antiaircraft trajectory correction projectile［J］.Transactions of Beijing Institute of Technology，2011，31（10）：1 184－1 188.（in Chinese）

［4］葛贤坤.末段修正火箭弹脉冲修正技术［J］.弹道学报，2006，18（4）：29－32.GE Xian－kun.Impulse correction technology for terminal correction rocket［J］.Journal of Ballistics，2006，18（4）：29－32.（in Chinese）

［5］FRESCONI F，COOPER G.Practical assessment of real－time impact point estimators for smart weapons［J］.Journal of Aerospace Engineering，2010，12（1）：1－29.

［6］杨绍卿.火箭外弹道偏差与修正理论［M］.北京：国防工业出版社，2011.YANG Shao－qing.Trajectory error and correction theory of rockets［M］.Beijing：National Defense Industry Press，2011.（in Chinese）