基于Fluent的水气两相流的数值模拟

李 鹏 陈 铭 李明然

在水利工程中，因水流水头高、流速大、紊动强、水流表面或过流边界突变，造成大量的空气掺入水流中，形成水气两相流，称之为掺气水流。随着计算机技术的迅速发展，计算流体力学的数值模拟技术有了很大发展。本文以Fluent6.2软件为基础，采用标准紊流模型，对明渠水气两相流进行了数值模拟研究。

1. 模型建立及边界条件

根据实验工况，计算实例如图1所示。明渠坡度为45°，槽长16.50m，槽宽0.20m，入口水深为8.0cm，流量为100L/s。分别对明渠陡槽的4个断面（离入口的距离分别为6m、9m、13m和15m）的流速、紊动、掺气浓度能进行计算。

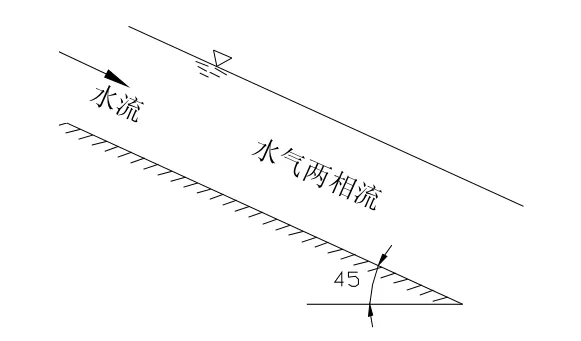
图1 明渠水气两相流计算模型

数值模拟网格用Fluent的Gambit前处理软件生成，采用四边形非均匀结构化网格。水流入口的边界分为空气进口和水进口两部分，其中，空气进口边界设定为压力边界条件，水进口边界设定为速度入口边界，其压力均为标准大气压。由于不知道出库水深，气体和水流的边界无法分开，只能作为单独出口边界处理，采用压力出口边界。壁面采用无滑移边界，即U=0、V=0，近壁区，雷诺数较小，在粘性底层用壁函数处理。

2.控制方程及数值计算方法

2.1 控制方程

连续方程：

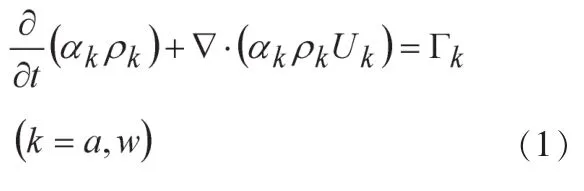
式中：下标a表示气相，w表示水相，α 为容积分数，ρk为相密度，Uk为相速度，Γk为界面质量传输率。

动量方程：

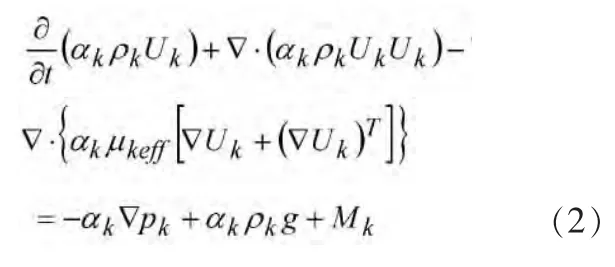
式中：p为压强，g为重力加速度，μkeff为有效粘性系数，μkeff=μk+μt， 各相涡粘性系数 μt=Cμtρk2/ε，Mk为相间作用力。

k方程：

其中：

ε方程：

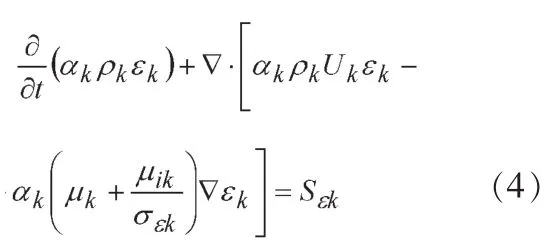
2.2 数值计算方法

采用控制体积法对偏微分形式的控制方程组进行离散，得到代数形式的方程组，然后采用迭代法对方程求解。其中离散采用标准格式，压力与速度的耦合采用SIMPLE方法计算。当计算各变量残差小于1.0×10-4或残差随迭代次数的增加基本不变化时，可认为计算收敛。

3. 计算结果分析

3.1 掺气浓度

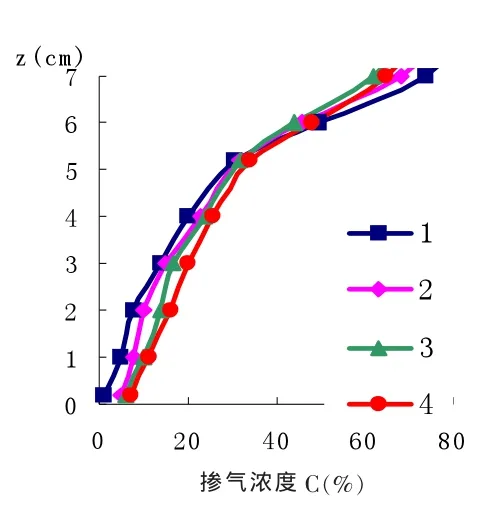
图2不同断面掺气浓度分布图1-下游6m，2-下游9m，3-下游 13m，4-下游 15m

计算得到的4个断面的掺气浓度分布如图2所示。从图中可以看出，掺气浓度沿程增加，并且在明渠底部增加幅度较小，而在上部增加幅度较大。每个断面掺气浓度变化特性是自渠底向水面逐渐增加。

3.2 流速分布

图3 不同断面流速分布图1-下游6m，2-下游9m，3-下游13m，4-下游15m

从图3中可以看出，计算的掺气水流流速沿程逐渐增大，同一断面流速自底面向水面不断增大，随后逐渐减小，与理论预测一致。流速自底面向水面方向不断增大，其原因为边壁的阻力作用，掺气只能影响其变化梯度，在靠近水面的部分区域，流速沿垂向不断减小，主要是受到掺气的影响，掺气使气体边界对水流速度的影响深入到了水流内部。

3.3 紊动能

从图4中看出水相紊动能在靠近壁面处大，为平均动能的90%左右，靠近水面处较小，且沿程有增大趋势，且增加非常缓慢，这与理论分析结果相一致。从图5可看出气相紊动能在不同断面上的分布情况。图中可以看出，水相与气相的紊动能分布规律相同，大小极为接近。

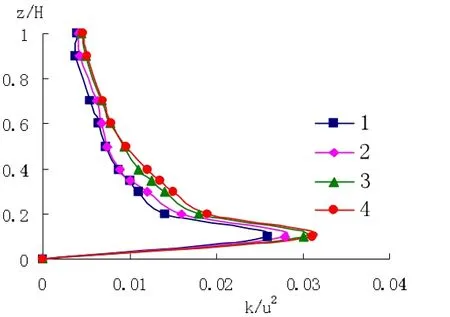
图5 气相紊动能在不同断面的分布图1-下游6m，2-下游9m，3-下游13m，4-下游15m

4. 结论

图4 水相紊动能在不同断面的分布图1-下游 6m，2-下游9m，3-下游 13m，4-下游 15m

一是本文采用Fluent软件中的紊流模型，利用VOF方法确定自由表面计算水气两相流是合理的。二是采用Fluent软件计算的水相及气相紊动能在靠近壁面处较大，随水深增加逐渐减小。由于没有紊动能分布的试验资料，因此准确性还需进一步验证。